蓝桥杯上岸每日N题 第七期(小猫爬山)!!!
蓝桥杯上岸每日N题 第七期(小猫爬山)!!!
同步收录 👇
蓝桥杯上岸必背!!!(第四期DFS)
大家好 我是寸铁💪
冲刺蓝桥杯省一模板大全来啦 🔥
蓝桥杯4月8号就要开始了 🙏
距离蓝桥杯省赛倒数第3天 ❗️ ❗️ ❗️
还没背熟模板的伙伴们背起来 💪 💪 💪
真题千千万万遍,蓝桥省一自然现! ✌️
日更3000里,蓝桥眷顾你 🌟
暴力出奇迹,打表过样例 👊
祝大家4月8号蓝桥杯上岸 ☀️
不清楚蓝桥杯考什么的点点下方👇
考点秘籍
想背纯享模版的伙伴们点点下方👇
蓝桥杯省一你一定不能错过的模板大全(第一期)
蓝桥杯省一你一定不能错过的模板大全(第二期)
蓝桥杯省一你一定不能错过的模板大全(第三期)
蓝桥杯省一你一定不能错过的模板大全(第四期)!!!
想背注释模版的伙伴们点点下方👇
蓝桥杯必背第一期
蓝桥杯必背第二期
往期精彩回顾
蓝桥杯上岸每日N题 第一期(一)!!!
蓝桥杯上岸每日N题第一期(二)!!!
蓝桥杯上岸每日N题第一期(三)!!!
蓝桥杯上岸每日N题第二期(一)!!!
蓝桥杯上岸每日N题第三期(一)!!!
蓝桥杯上岸每日N题 第四期(最少刷题数)!!!
蓝桥杯上岸每日N题 第五期(山)!!!
蓝桥杯上岸每日N题 第六期(求阶乘)!!!
操作系统期末题库 第九期(完结)
LeetCode Hot100 刷题(第三期)
idea创建SpringBoot项目报错解决方案
数据库SQL语句(期末冲刺)
想看JavaB组填空题的伙伴们点点下方 👇
填空题
竞赛干货
算法竞赛字符串常用操作大全
蓝桥杯上岸必刷!!!(模拟/枚举专题)
蓝桥杯上岸必背!!! (第三期 DP)
蓝桥杯上岸必背!!!(第四期DFS)
蓝桥杯上岸必背!!!(第五期BFS)
蓝桥杯上岸必背!!!(第六期树与图的遍历)
蓝桥杯上岸必背!!!(第七期 最短路算法)
蓝桥杯上岸必背!!!(第八期 简单数论)
喜欢的小伙伴可以关注我,关注寸铁,我们一起上岸4.8蓝桥杯!!!
小猫爬山
考点:DFS+可行性剪枝
分析
要尽可能减少花费-->递归的分支尽可能少-->优先考虑放重猫
优先考虑放重猫,需要从大到小排个序,
一直往下搜索,答案是唯一的。
放得下猫就继续往该车往下加
放不下就再另外开一辆放猫
分两个分支去放
开一辆继续放其他猫的为一个分支
开另一辆单独只放一只猫的为另一个分支
接下来递归调用处理,对于每个分支递归后有又n个分支,一直递归下去,直至递归到n层。说明当前的车数为最优解。
我们可以建立如下递归搜索图:
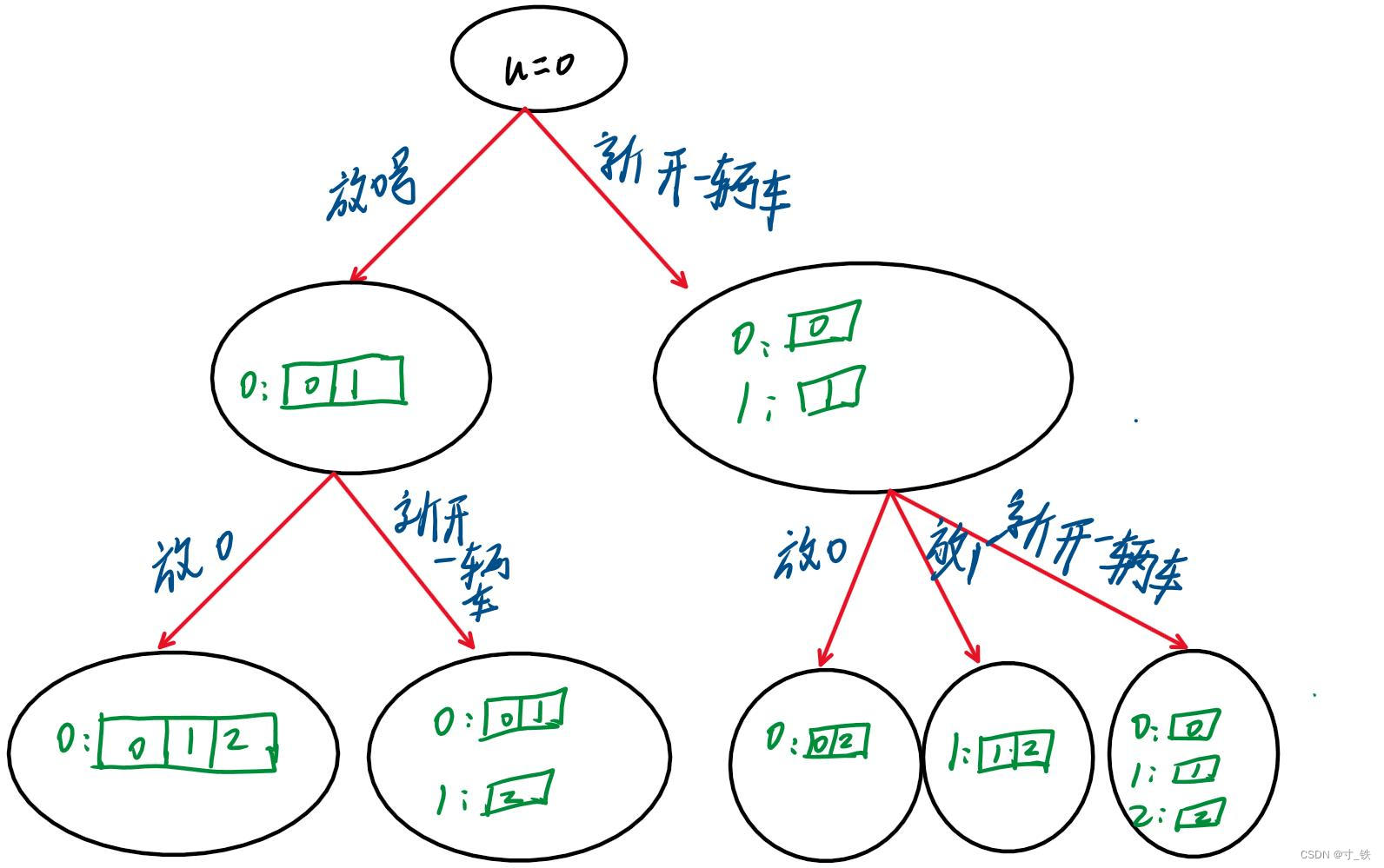
DFS小结:
递归DFS最简单直接的理解方式就是按照你的做题逻辑顺序来写
所以做题的逻辑顺序至关重要,确保不重不漏地确保方案。
逻辑正确跑出来答案正确即可,不要过分地去深究内在实现,会很纠结。
注意dfs下一层要恢复现场,这是必需的。
深究不外乎:递归下一层+置false回溯上一层用+去掉无用的分支剪枝
Accode
//从大到小排个序,优先放重猫。
//一直往下搜索,答案是唯一的。
//放得下猫就继续往下加
//放不下就再另外开一辆,继续放
//分两个分支去放
//开一辆继续放其他猫的有一个分支
//开另一辆只放一只猫的也有一个分支
import java.util.*;
public class Main{static int N=20;static int n,m;static int arr[]=new int [N];static int ans=N;static int car[]=new int [N];static int cat[]=new int[N];public static void main(String []args){Scanner in = new Scanner(System.in);n=in.nextInt();m=in.nextInt();for(int i=0;i<n;i++)cat[i]=in.nextInt();Arrays.sort(arr,0,n);//从小到大排个序Reverse(arr,0,n-1);//再从大到小排个序,优先放重猫dfs(0,0);System.out.println(ans);}//直接把他看成是第一遍模拟,剩下的递归处理即可。public static void dfs(int u,int k){if(k>=ans)return;if(u==n){//走到n时,即为找到答案ans=当前小车的数量kans=k;return;}//考虑猫都放一辆车的情况for(int i=0;i<k;i++){if(cat[u]+car[i]<=m){car[i]+=cat[u];dfs(u+1,k);car[i]-=cat[u];//恢复现场,便于下一次加猫操作}}//考虑猫只放一辆车的情况car[k]=cat[u];dfs(u+1,k+1);//每次dfs会用到一辆车,所以需要加一。car[k]=0;//恢复现场}public static void Reverse(int q[],int l,int r)//反转函数 -->从大到小排个序{for(int i=l,j=r;i<j;i++,j--){int temp=arr[i];arr[i]=arr[j];arr[j]=temp;}}}
✨ ✨ ✨
看到这里,不妨点个关注 💖
相关文章:

蓝桥杯上岸每日N题 第七期(小猫爬山)!!!
蓝桥杯上岸每日N题 第七期(小猫爬山)!!! 同步收录 👇 蓝桥杯上岸必背!!!(第四期DFS) 大家好 我是寸铁💪 冲刺蓝桥杯省一模板大全来啦 🔥 蓝桥杯4月8号就要开始了 &a…...
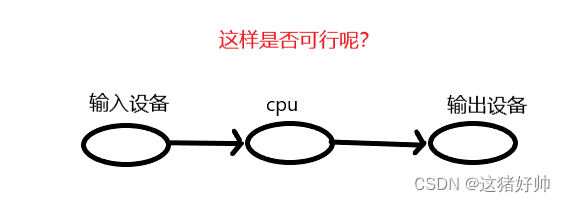
【Linux系统编程】冯诺依曼体系结构
目录 前言 什么是冯诺依曼体系结构? 冯诺依曼体系结构如何进行数据处理的? 存储器在冯诺依曼体系中有什么作用? 冯诺依曼体系结构为什么要这样设计? 冯诺依曼结构总结 前言 相信对于冯诺依曼这个人的名字大家一定不会感到陌…...
数据结构--动态顺序表
文章目录 线性表动态顺序表数组与顺序表 接口实现初始化:尾插:尾删头插头删指定位置插入指定位置删除查找摧毁 完整代码 线性表 线性表是数据结构中最基本、最简单也是最常用的一种数据结构。线性表是指由n个具有相同数据类型的元素组成的有限序列。 线…...
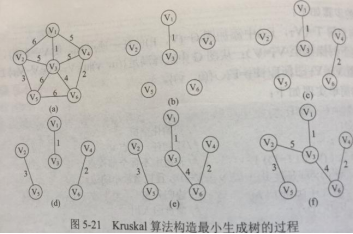
笔试数据结构选填题
目录 卡特兰数Catalan:出栈序列/二叉树数 树 二叉树 N01N2 哈夫曼树(最优二叉树)Huffman 度m的哈夫曼树只有度为0和m的结点:Nm(n-1)/(m-1) 平衡二叉树AVL Nh表示深度为h最少结点数,则N00,N11&#…...

# 鸢尾花的案例学习
# 鸢尾花的案例学习 # 1. 导入小型的数据 from sklearn.datasets import load_iris import numpy as np import pandas as pd import seaborn as sbn import matplotlib.pyplot as plt # 2. 获取数据 irisload_iris() # 3.查看数据print("数据集\n ",len(iris.d…...

线程、进程的区别
线程、进程的区别 在开发中,我们经常听到线程和进程两个概念,它们都是操作系统的基本概念,操作系统以进程为基本单位分配存储器,以线程为基本单位分配CPU。虽然它们有很多相似之处,但是它们也有很大的区别。本文将详细…...

在 Ubuntu 上安装 Docker 桌面
Ubuntu 22.04 (LTS) 安装 Docker 桌面 要成功安装 Docker Desktop,您必须: 满足系统要求拥有 64 位版本的 Ubuntu Jammy Jellyfish 22.04 (LTS) 或 Ubuntu Impish Indri 21.10。对于非 Gnome 桌面环境,必须安装 gnome-terminal:…...
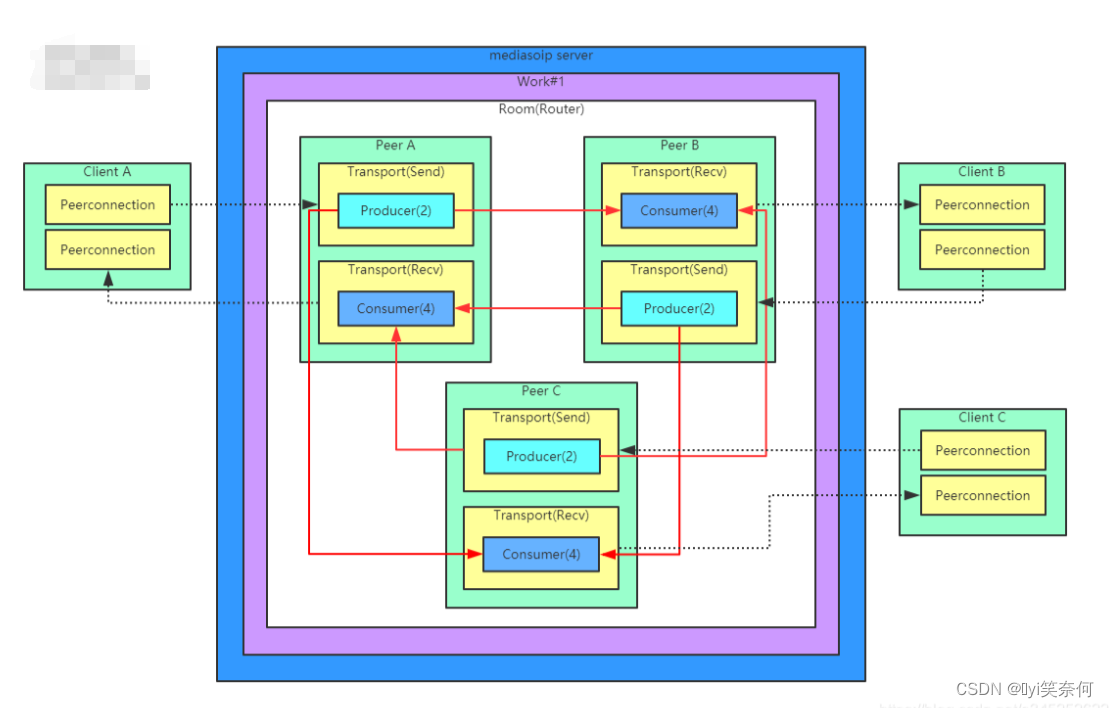
【WebRTC---序篇】(七)RTC多人连麦方案
服务端可以选择mediasoup,作为SFU服务器,只负责转发数据 下图举例三个Client (browser或者客户端)同时加入一个房间,每个app同时发布一路视频和一路音频,并且接受来自其他app的音视频流,mediasoup内部的结构如下&…...

【Java可执行命令】(十六)诊断命令请求发送工具 jcmd:提供一种简单而强大的方式来管理和监控 Java 进程 ~
Java可执行命令之jcmd 1️⃣ 概念2️⃣ 优势和缺点3️⃣ 使用3.1 语法格式3.2 jcmd -l:列出正在运行的 Java 进程3.3 jcmd < pid> help:列出特定进程的诊断命令列表3.4 jcmd < pid> < command>:执行诊断命令 4️⃣ 应用场景…...

如何创建无序列表和有序列表?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 无序列表⭐ 无序列表⭐ 注意事项⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅!这个专栏是为那些对Web开发感兴…...
【MongoDB】初识、安装MongoDB
目录 一、MongoDB主要应用场景 二、MongoDB简介 三、MongoDB相关特点 四、MongoDB的安装 一、MongoDB主要应用场景 传统的数据库如MySQL在应对三高场景时显得力不从心 三高: High performance 对数据库高并发读写的需求 High Storage 对海量数据的高效率存储和 …...
方法区内存溢出及常量池
22 方法区-定义 是所有线程共享的一块区域。 存储了和类结构相关信息。运行时常量池, 方法区在虚拟机启动时被创建,逻辑上是堆的组成部分。方法区内存不足,也会导致oom异常。 是一个概念上的东西, 1.6使用永久代作为方法区&#…...

【MTK平台】【wpa_supplicant】关于wpa_supplicant_8/src/p2p/p2p_invitation.c文件的介绍
本文主要介绍external/wpa_supplicant_8/src/p2p/p2p_invitation.c文件 这里主要介绍6个方法 1.p2p_invite //p2p邀请调用此方法 2.p2p_invite_send //对p2p_invite方法进行补充 3. p2p_process_invitation_resp 4.p2p_process_invitation_req 5.p2p_build_invitation_re…...
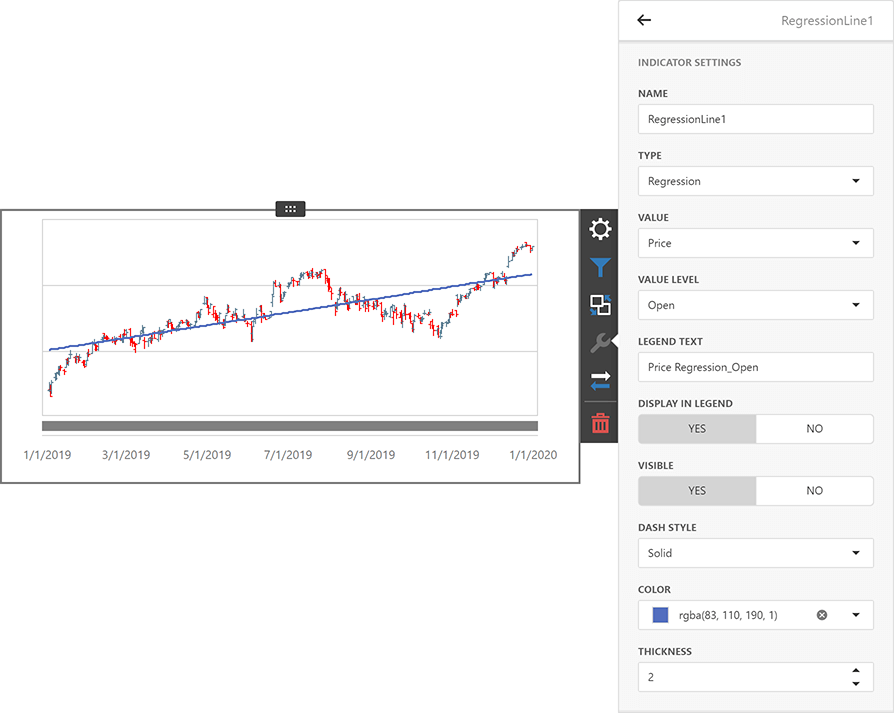
智能仪表板DevExpress Dashboard v23.1亮点 - 增强对自定义导出的支持
DevExpress Dashboard v23.1版本增强了自定义导出到Excel的功能等,欢迎下载最新版本体验! DevExpress Dashboard v23.1正式版下载(Q技术交流:523159565) 所有平台 导出自定义仪表板项目到Excel 用户现在可以在WinForms和Web应…...

分布式应用:ELK企业级日志分析系统
目录 一、理论 1.ELK 2.ELK场景 3.完整日志系统基本特征 4.ELK 的工作原理 5.ELK集群准备 6.Elasticsearch部署(在Node1、Node2节点上操作) 7.Logstash 部署(在 Apache 节点上操作) 8.Kiabana 部署(在 Node1 节点…...
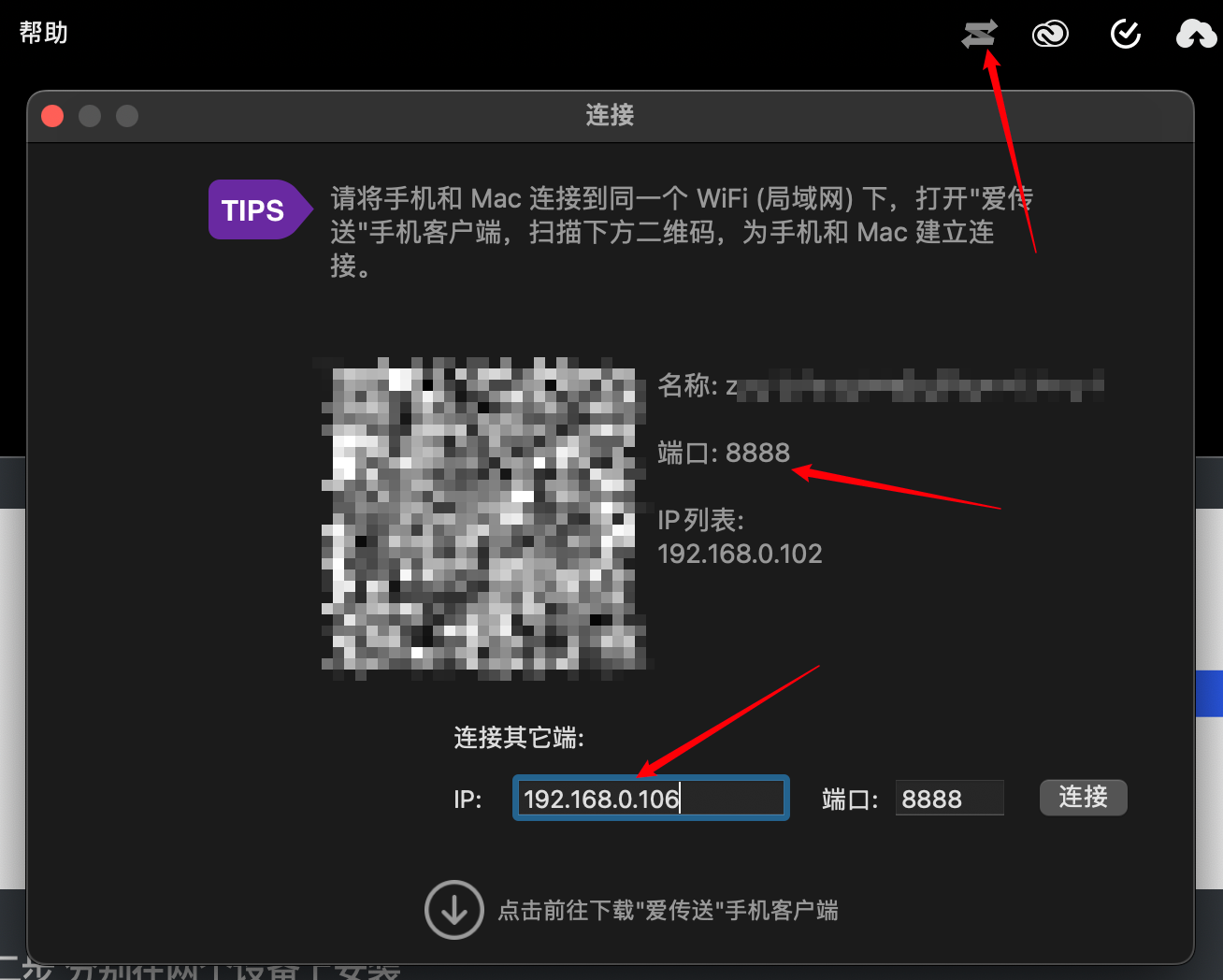
Mac与windows传文件(超过4G且速度超快,非共享)
MAC与Windows文件互传 背景 尝试了网上的一些方法,诸如设置共享文件夹方法等,但是实际使用中感觉效果一般,对于一些小的文件共同编辑速度还可以。但是在备份或者传递一些较大文件或者很多细小文件的时候就有点捉襟见肘了。制作了一个MAC可读…...
2023年第四届“华数杯”数学建模思路 - 案例:退火算法
## 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 退火算法原理 1.1 物理背景 在热力学上,退火(annealing)现象指物体逐渐降温的物理现象,温度愈低&#…...
)
STM32 UDS Bootloader开发-上位机篇-CANoe制作(3)
文章目录 前言刷写脚本34服务写入数据的实现定时函数writeBlockData函数Checksum总结前言 上一篇文章中介绍了CAPL刷写脚本的大部分内容,本文继续介绍34,36,37服务的实现,及checksum中遇到的坑 刷写脚本 34服务 void requestDownLoad(struct Block hexfile) {gTxBuffer[…...
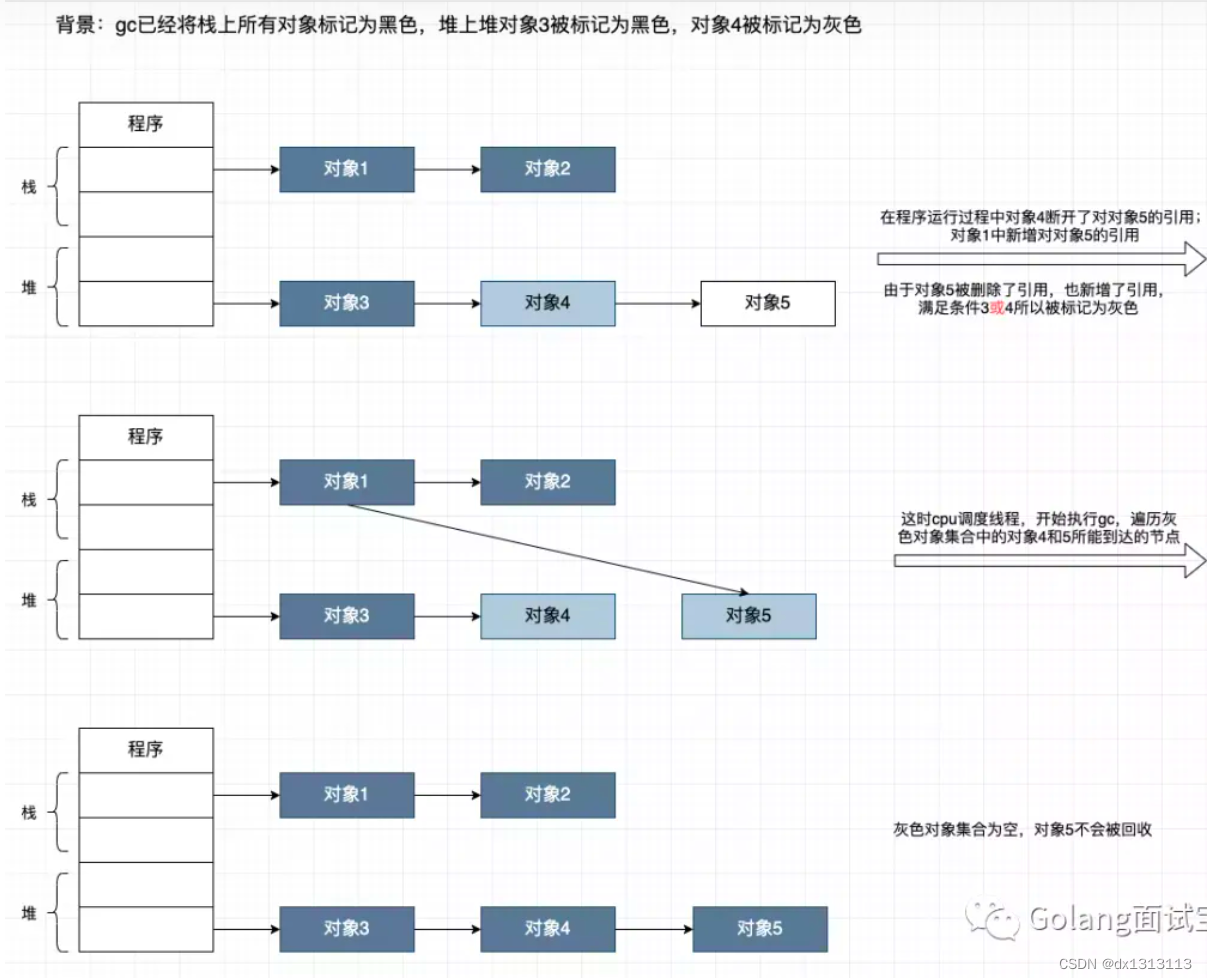
GO语言的垃圾回收机制
内存垃圾的产生 程序在内存上被分为堆区、栈区、全局数据区、代码段、数据区五个部分。对于C等早期编程语言栈上的内存回由编译器负责管理回收,而堆上的内存空间需要编程人员负责申请和释放。在Go中栈上内存仍由编译器负责管理回收,而堆上的内存由编译器…...
vim粘贴内容格式混乱解决方法
问题 复制本地文件内容后,咱贴到vim文本内,格式错乱 解决方法 打开vim配置文件 最后面加入一行 vim /etc/vimrc set pastetoggle<F11> 开发vim文件,进入后先按F11进入交互模式 shift insert 再次粘贴 解决...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

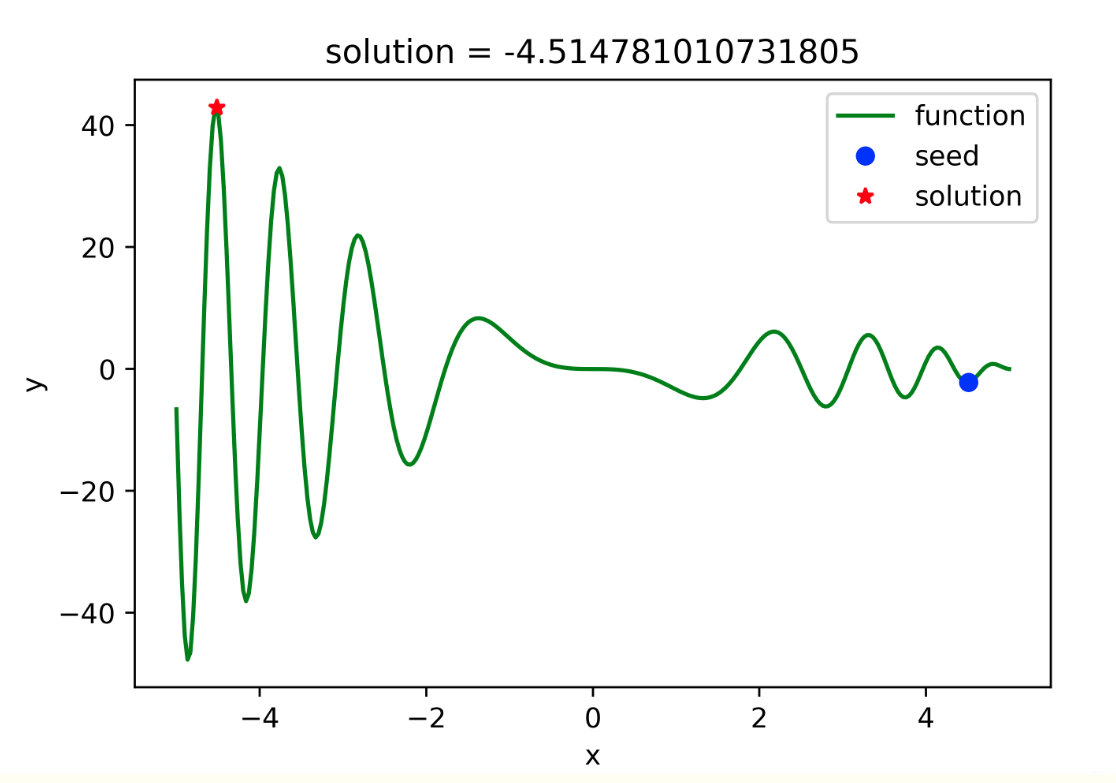
三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...
