笔试数据结构选填题
目录
卡特兰数Catalan:出栈序列/二叉树数
树
二叉树
N0=1+N2
哈夫曼树(最优二叉树)Huffman
度m的哈夫曼树只有度为0和m的结点:Nm=(n-1)/(m-1)
平衡二叉树AVL
Nh表示深度为h最少结点数,则N0=0,N1=1,N2=2,Nh=Nh-1+Nh-2+1
最小生成树
图
最短路径
模式匹配
BF模式匹配:最坏T(n)=O(m*n),实际 接近O(m+n)
KMP模式匹配:O(m+n)
完整见:前端笔试常考设计模式,操作系统,数据结构,ACM模板,经典算法,正则表达式,常用方法_前端考试模板_参宿7的博客-CSDN博客
卡特兰数Catalan:出栈序列/二叉树数
一个栈的进栈序列为1,2,3,...,n,有多少个不同的出栈序列:
合法的出栈序列的数量=出栈序列的总数-非法序列的数量
∵先序+中序 可 唯一 确定 一棵二叉树
其关系 就如 入栈序列+出栈序列 可 唯一 确定 一个 栈
∴先序 确定 二叉树个数,即先序 确定 中序个数,
NLR确定LNR,LN、NL相当于压栈,R相当于进了立即出
∴h(n)=Catalan卡特兰数=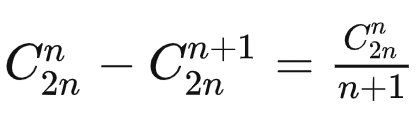
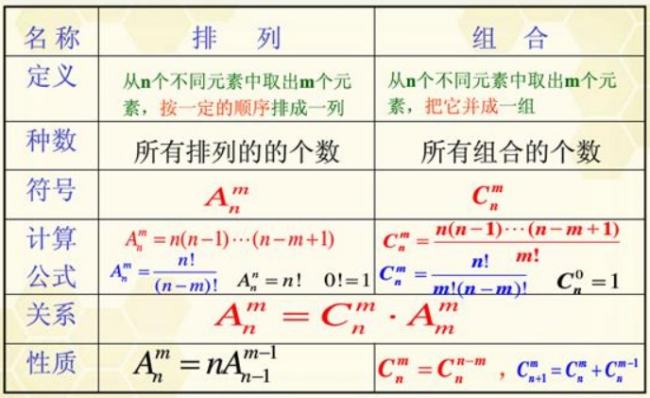
树
二叉树
N0=1+N2
哈夫曼树(最优二叉树)Huffman
度m的哈夫曼树只有度为0和m的结点:Nm=(n-1)/(m-1)
平衡二叉树AVL
Nh表示深度为h最少结点数,则N0=0,N1=1,N2=2,Nh=Nh-1+Nh-2+1
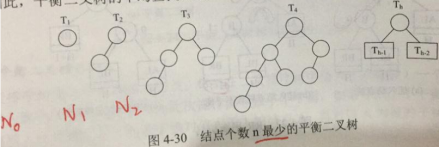
最小生成树
- 定义:连通,无向带权 图 的生成树,权值之和最小的
- 唯一:当任意环中边的权值相异,则最小生成树唯一
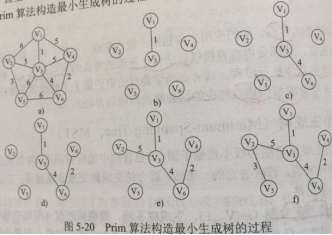
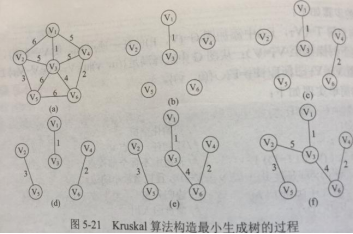
| 普里姆Prim算法 | 克鲁斯卡Kruskal算法 | |
| 共同 | 基于贪心算法 | |
| 特点 | 从顶点开始扩展最小生成树 | 按权递增次序,选择不构成环的边 |
图
最短路径
| Dijkstra算法 | Floyd算法 | |
| 问题 | 单源最短路径(单起源到各个顶点的最短距离,从源点的临近点开始) | 各个顶点之间的最短路径 |
模式匹配
主串S,长n,模式串T,长m。T在S中首次出现的位置
BF/朴素模式匹配:最坏T(n)=O(m*n),实际 接近O(m+n)
KMP模式匹配:O(m+n)
- next[j]:T的第j个字符失配于S中的第i个字符,需要用T的第next[j]个字符与S中的第i个字符 比较
abcdeabf(f失配,第next[j]=3个字符c比较)T起点开始,和失配点结束的最大公共前缀
- next[1]=0:i++;
- next[2]=1,next[j]:i不变;
模式匹配过程:
- S中第i个char,T中第j个char
- j指向 失配点/ j=m(全部匹配成功) 为 一趟
虽KMP的T(n)=O(m+n),
但实际中BF的T(n)接近O(m+n),
∴至今采用
只有T中有很多部分匹配,KMP才明显快
相关文章:

笔试数据结构选填题
目录 卡特兰数Catalan:出栈序列/二叉树数 树 二叉树 N01N2 哈夫曼树(最优二叉树)Huffman 度m的哈夫曼树只有度为0和m的结点:Nm(n-1)/(m-1) 平衡二叉树AVL Nh表示深度为h最少结点数,则N00,N11&#…...

# 鸢尾花的案例学习
# 鸢尾花的案例学习 # 1. 导入小型的数据 from sklearn.datasets import load_iris import numpy as np import pandas as pd import seaborn as sbn import matplotlib.pyplot as plt # 2. 获取数据 irisload_iris() # 3.查看数据print("数据集\n ",len(iris.d…...

线程、进程的区别
线程、进程的区别 在开发中,我们经常听到线程和进程两个概念,它们都是操作系统的基本概念,操作系统以进程为基本单位分配存储器,以线程为基本单位分配CPU。虽然它们有很多相似之处,但是它们也有很大的区别。本文将详细…...

在 Ubuntu 上安装 Docker 桌面
Ubuntu 22.04 (LTS) 安装 Docker 桌面 要成功安装 Docker Desktop,您必须: 满足系统要求拥有 64 位版本的 Ubuntu Jammy Jellyfish 22.04 (LTS) 或 Ubuntu Impish Indri 21.10。对于非 Gnome 桌面环境,必须安装 gnome-terminal:…...
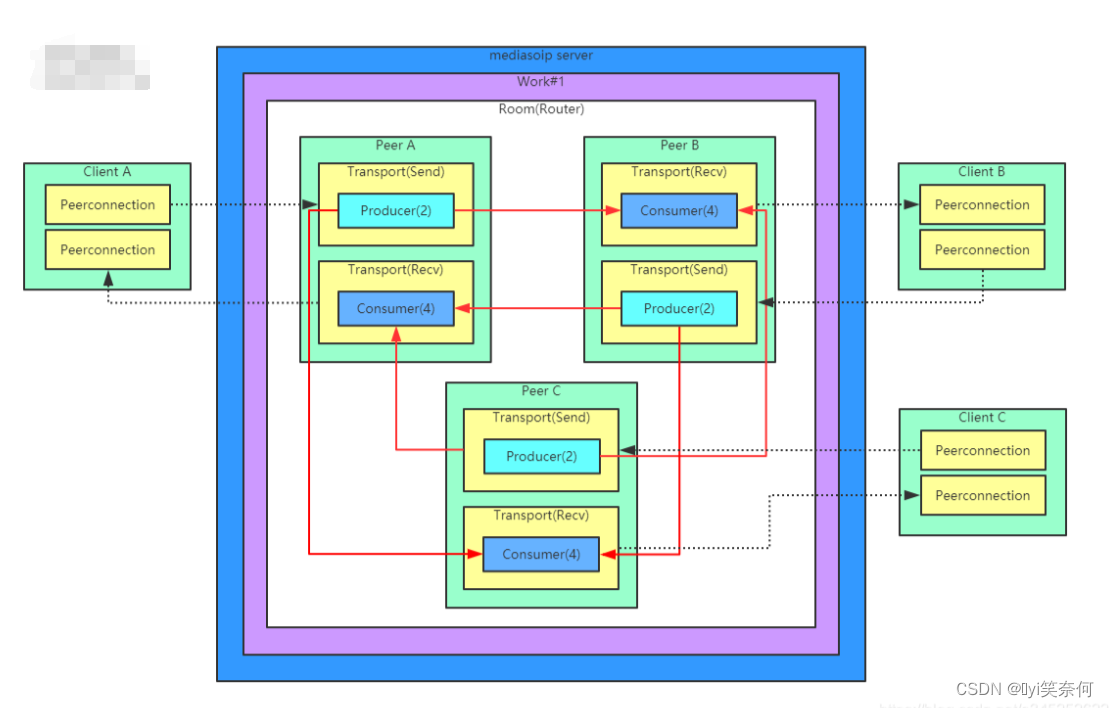
【WebRTC---序篇】(七)RTC多人连麦方案
服务端可以选择mediasoup,作为SFU服务器,只负责转发数据 下图举例三个Client (browser或者客户端)同时加入一个房间,每个app同时发布一路视频和一路音频,并且接受来自其他app的音视频流,mediasoup内部的结构如下&…...

【Java可执行命令】(十六)诊断命令请求发送工具 jcmd:提供一种简单而强大的方式来管理和监控 Java 进程 ~
Java可执行命令之jcmd 1️⃣ 概念2️⃣ 优势和缺点3️⃣ 使用3.1 语法格式3.2 jcmd -l:列出正在运行的 Java 进程3.3 jcmd < pid> help:列出特定进程的诊断命令列表3.4 jcmd < pid> < command>:执行诊断命令 4️⃣ 应用场景…...

如何创建无序列表和有序列表?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 无序列表⭐ 无序列表⭐ 注意事项⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅!这个专栏是为那些对Web开发感兴…...
【MongoDB】初识、安装MongoDB
目录 一、MongoDB主要应用场景 二、MongoDB简介 三、MongoDB相关特点 四、MongoDB的安装 一、MongoDB主要应用场景 传统的数据库如MySQL在应对三高场景时显得力不从心 三高: High performance 对数据库高并发读写的需求 High Storage 对海量数据的高效率存储和 …...
方法区内存溢出及常量池
22 方法区-定义 是所有线程共享的一块区域。 存储了和类结构相关信息。运行时常量池, 方法区在虚拟机启动时被创建,逻辑上是堆的组成部分。方法区内存不足,也会导致oom异常。 是一个概念上的东西, 1.6使用永久代作为方法区&#…...

【MTK平台】【wpa_supplicant】关于wpa_supplicant_8/src/p2p/p2p_invitation.c文件的介绍
本文主要介绍external/wpa_supplicant_8/src/p2p/p2p_invitation.c文件 这里主要介绍6个方法 1.p2p_invite //p2p邀请调用此方法 2.p2p_invite_send //对p2p_invite方法进行补充 3. p2p_process_invitation_resp 4.p2p_process_invitation_req 5.p2p_build_invitation_re…...
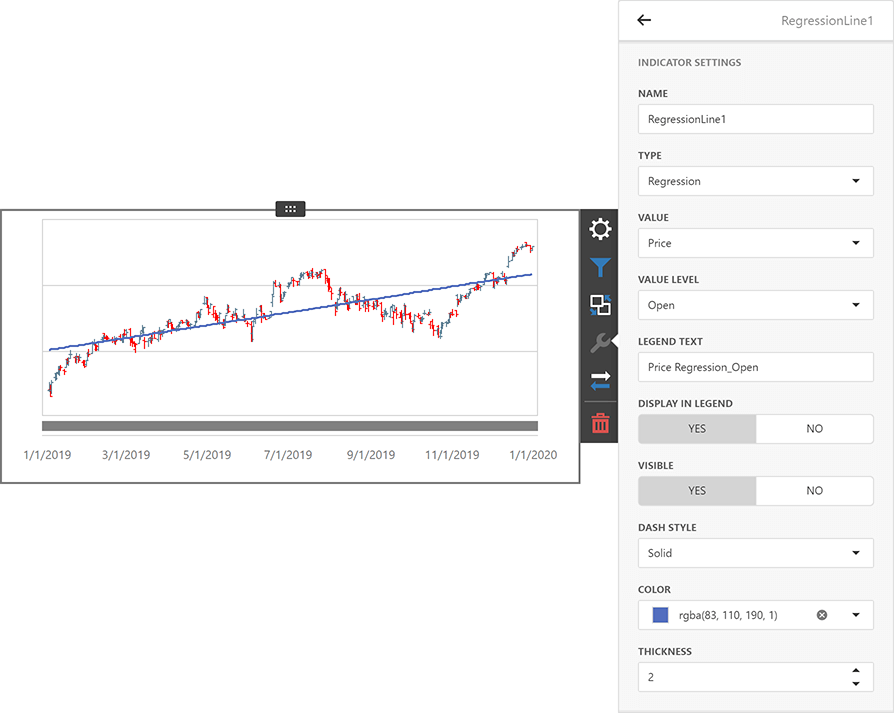
智能仪表板DevExpress Dashboard v23.1亮点 - 增强对自定义导出的支持
DevExpress Dashboard v23.1版本增强了自定义导出到Excel的功能等,欢迎下载最新版本体验! DevExpress Dashboard v23.1正式版下载(Q技术交流:523159565) 所有平台 导出自定义仪表板项目到Excel 用户现在可以在WinForms和Web应…...

分布式应用:ELK企业级日志分析系统
目录 一、理论 1.ELK 2.ELK场景 3.完整日志系统基本特征 4.ELK 的工作原理 5.ELK集群准备 6.Elasticsearch部署(在Node1、Node2节点上操作) 7.Logstash 部署(在 Apache 节点上操作) 8.Kiabana 部署(在 Node1 节点…...
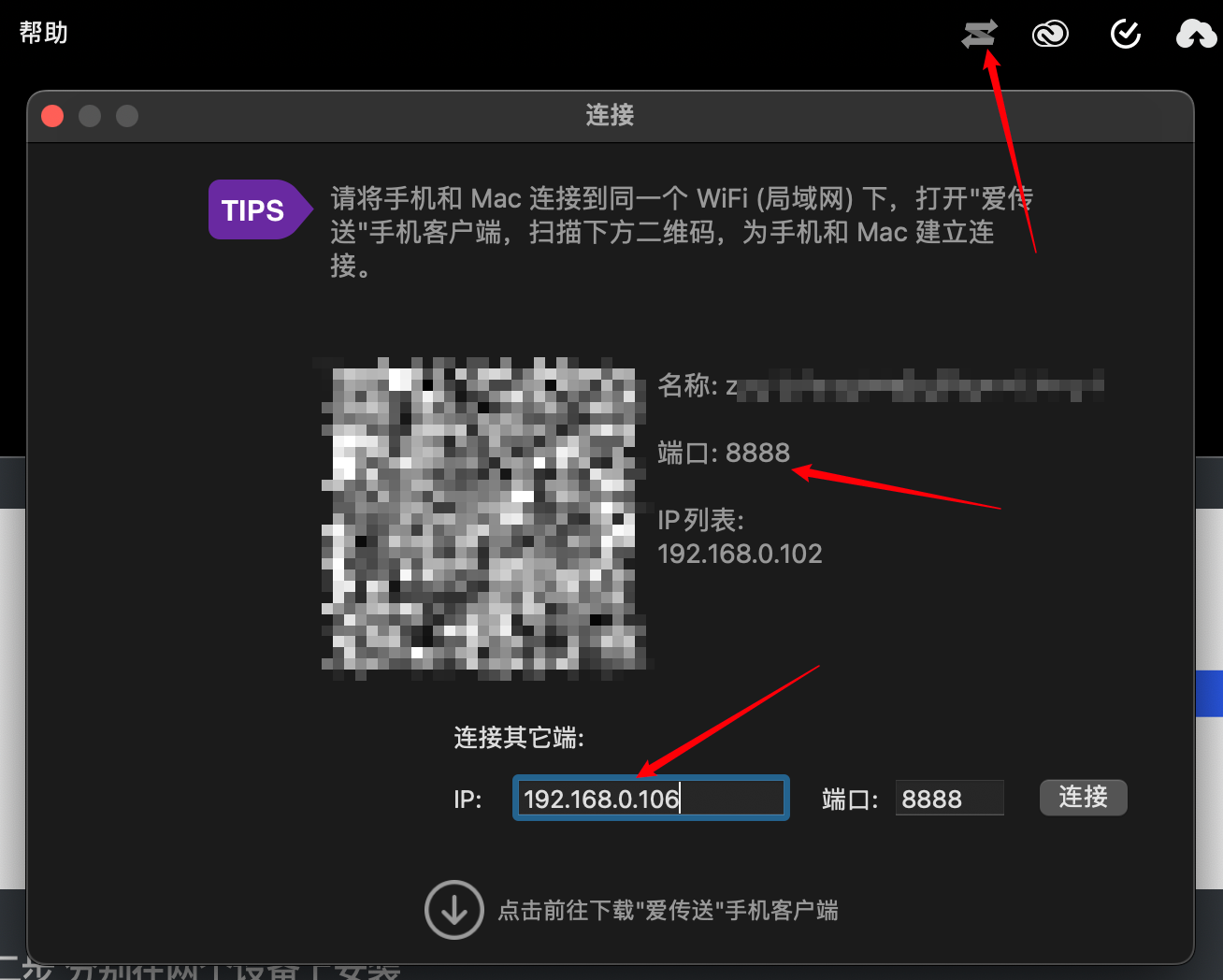
Mac与windows传文件(超过4G且速度超快,非共享)
MAC与Windows文件互传 背景 尝试了网上的一些方法,诸如设置共享文件夹方法等,但是实际使用中感觉效果一般,对于一些小的文件共同编辑速度还可以。但是在备份或者传递一些较大文件或者很多细小文件的时候就有点捉襟见肘了。制作了一个MAC可读…...
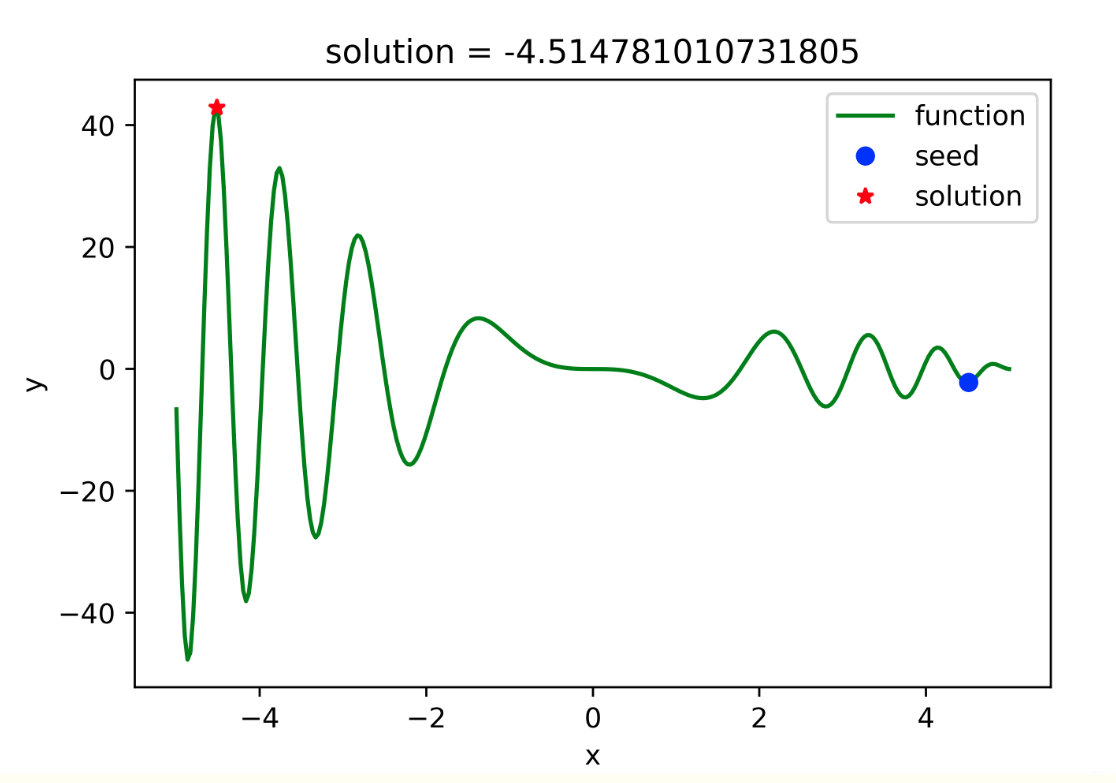
2023年第四届“华数杯”数学建模思路 - 案例:退火算法
## 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 退火算法原理 1.1 物理背景 在热力学上,退火(annealing)现象指物体逐渐降温的物理现象,温度愈低&#…...
)
STM32 UDS Bootloader开发-上位机篇-CANoe制作(3)
文章目录 前言刷写脚本34服务写入数据的实现定时函数writeBlockData函数Checksum总结前言 上一篇文章中介绍了CAPL刷写脚本的大部分内容,本文继续介绍34,36,37服务的实现,及checksum中遇到的坑 刷写脚本 34服务 void requestDownLoad(struct Block hexfile) {gTxBuffer[…...
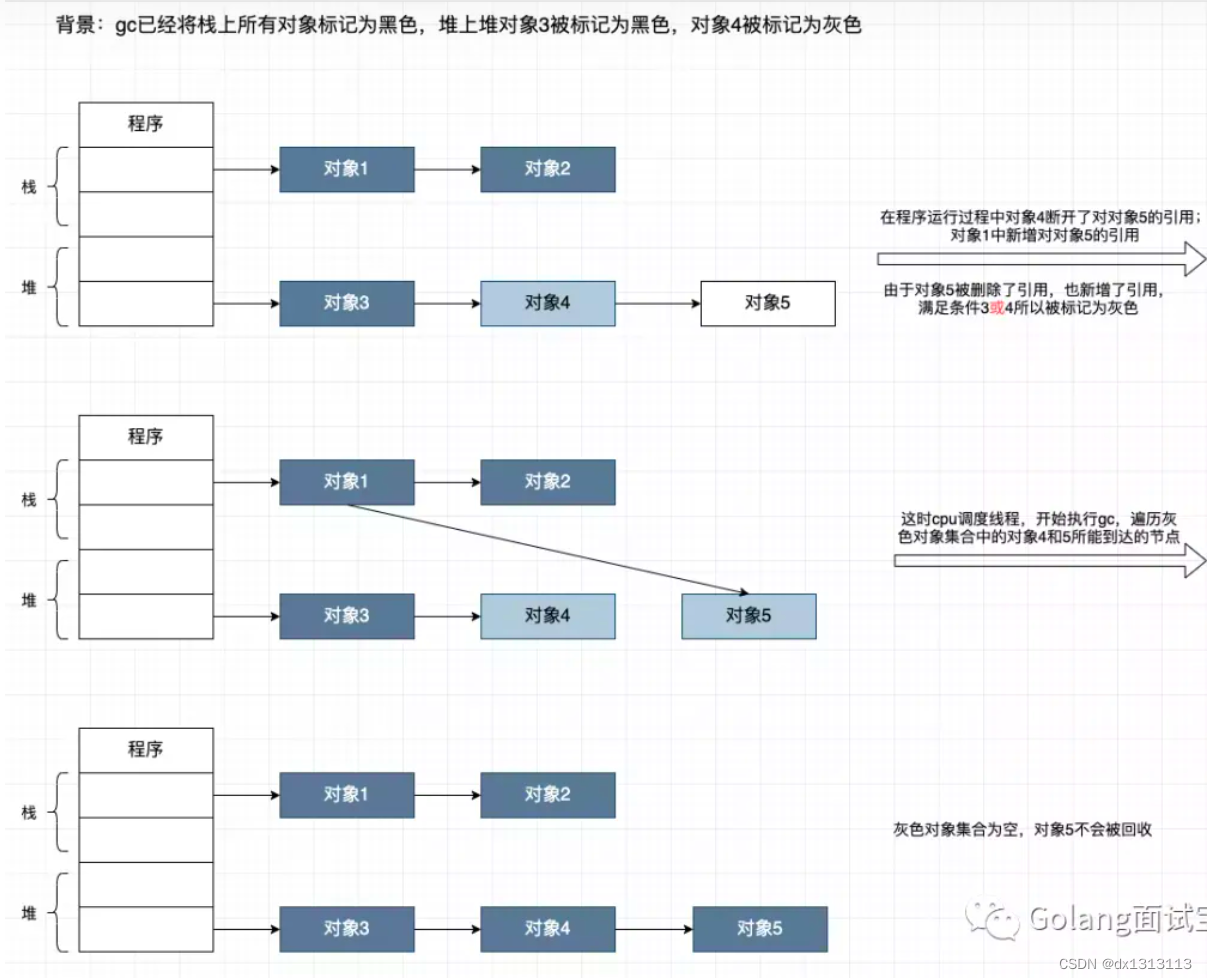
GO语言的垃圾回收机制
内存垃圾的产生 程序在内存上被分为堆区、栈区、全局数据区、代码段、数据区五个部分。对于C等早期编程语言栈上的内存回由编译器负责管理回收,而堆上的内存空间需要编程人员负责申请和释放。在Go中栈上内存仍由编译器负责管理回收,而堆上的内存由编译器…...
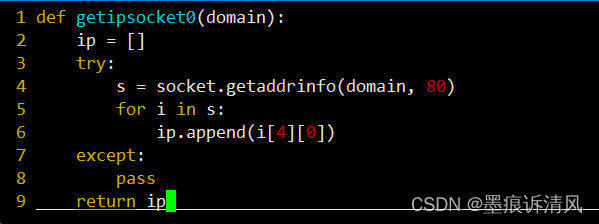
vim粘贴内容格式混乱解决方法
问题 复制本地文件内容后,咱贴到vim文本内,格式错乱 解决方法 打开vim配置文件 最后面加入一行 vim /etc/vimrc set pastetoggle<F11> 开发vim文件,进入后先按F11进入交互模式 shift insert 再次粘贴 解决...
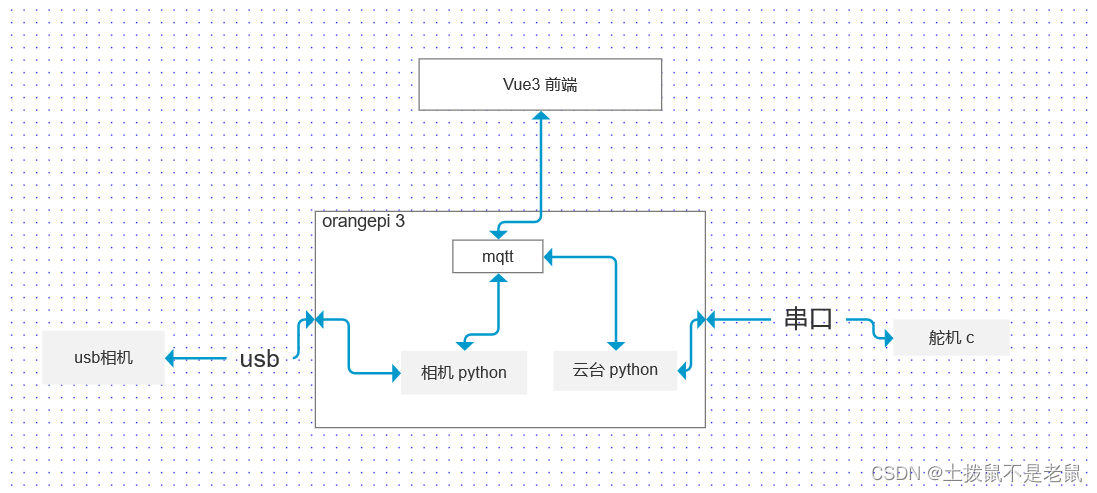
基于Orangepi 3 lts 的云台相机
利用orangepi 3 lts 和arduino nano 制作了一个云台相机,可用于室内监控。 硬件: orangepi 3 ,arduino nano ,usb相机,180度舵机两个 WeChat_20230806213004 软件: 整体采用mqtt进行消息的中转。 相机采用python 利用opencv…...

Go重写Redis中间件 - Go实现Redis持久化
GO实现Redis持久化 项目开发到这里,我们的下一步就是实现Redis的持久化落盘功能,Redis是一个内存型的数据库,在之前我们实现的单机版Redis如果把进程杀掉,我们通过GET、SET指令存储的数据都将不复存在,数据只存在内存的map里面,重启之后什么都没有了 我们现在的目标就是…...
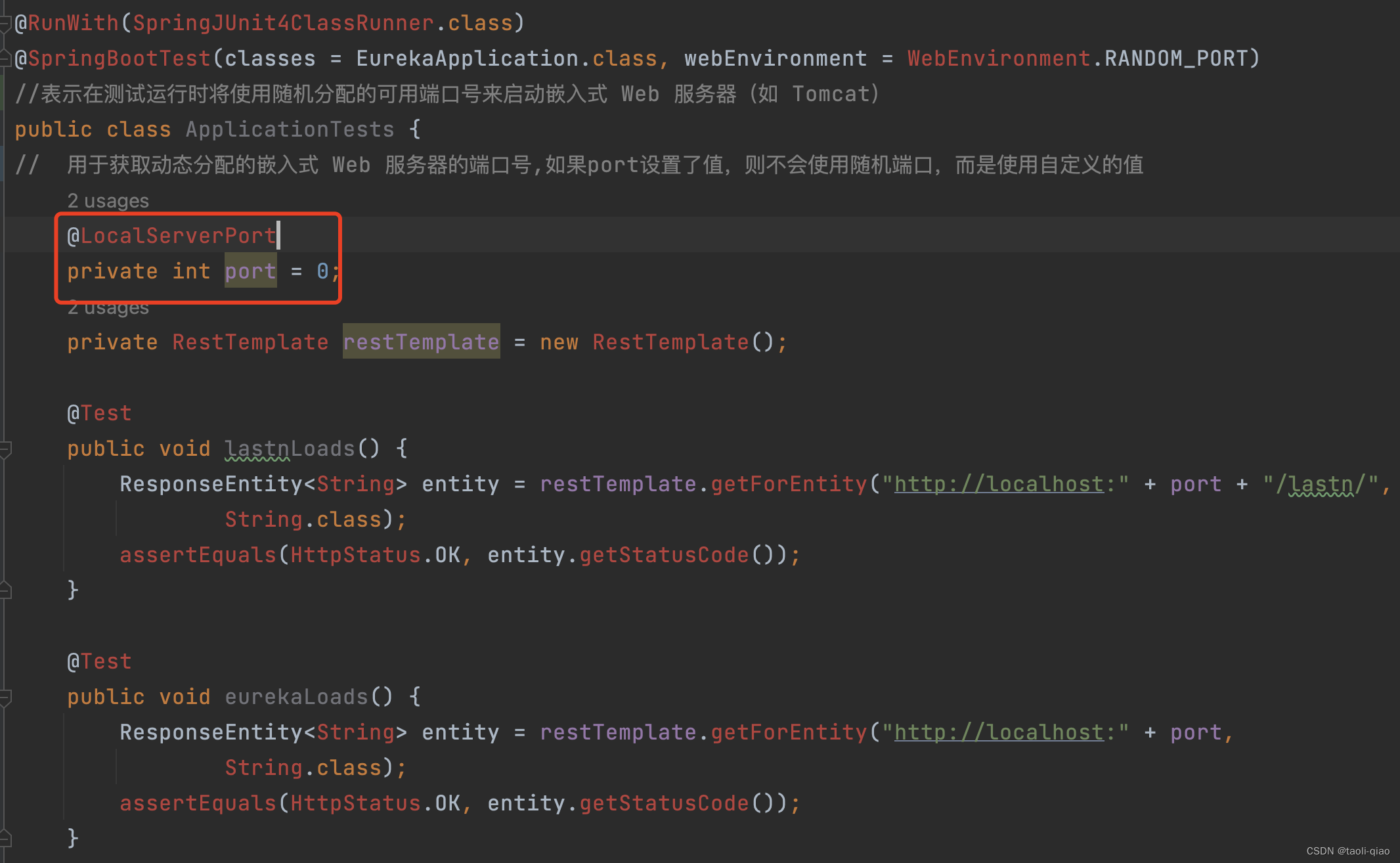
单元测试之 - Review一个微服务的单元测试
这里以github上一个microservice的demo代码为例,来看看如何为一个完整的服务编写单元测试。具体代码如下所示,我们重点查看一下catalog和customer,order中的单元测试有哪些。 首先来看catalog服务的单元测试,这个服务下面主要编写了CatalogWe…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

深入解析 ReentrantLock:原理、公平锁与非公平锁的较量
ReentrantLock 是 Java 中 java.util.concurrent.locks 包下的一个重要类,用于实现线程同步,支持可重入性,并且可以选择公平锁或非公平锁的实现方式。下面将详细介绍 ReentrantLock 的实现原理以及公平锁和非公平锁的区别。 ReentrantLock 实现原理 基本架构 ReentrantLo…...

第22节 Node.js JXcore 打包
Node.js是一个开放源代码、跨平台的、用于服务器端和网络应用的运行环境。 JXcore是一个支持多线程的 Node.js 发行版本,基本不需要对你现有的代码做任何改动就可以直接线程安全地以多线程运行。 本文主要介绍JXcore的打包功能。 JXcore 安装 下载JXcore安装包&a…...
