6.4.3 1x1卷积层
特点:1x1卷积层相当于全连接层
作用:1x1卷积用于调整网络层的通道数量和控制模型复杂度
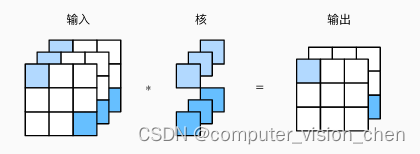 输入形状:(通道,行,列) = (3,3,3)
输入形状:(通道,行,列) = (3,3,3)
卷积核形状:(输出通道,输入通道,行,列) = (2,3,1,1)
输出形状:(通道,行,列) = (2,3,3)
import cv2
import torch
from torch import nn
from d2l import torch as d2l
一.使用神经网络全连接的方式实现对X使用1x1卷积
def corr2d_multi_in_out_1x1(X,K):c_i,h,w = X.shapec_o = K.shape[0]X = X.reshape((c_i,h*w))K = K.reshape((c_o,c_i))Y = torch.matmul(K,X)# 全连接层中的矩阵乘法return Y.reshape((c_o,h,w))
二.使用卷积函数计算 对X使用1x1卷积
def corr2d_multi_in(X,K):return sum(d2l.corr2d(x,k) for x,k in zip(X,K))
'''多输入和多输出通道'''
def corr2d_multi_in_out(X,K):# 注意,没有遍历X,此时的X是大写return torch.stack([corr2d_multi_in(X,k) for k in K],0)
# 生成均值为0,方差为1的 3通道的3x3矩阵
X = torch.normal(0,1,(3,3,3))
# 生成均值为0,方差为1的 输出通道为2,输入通道为3,3x3矩阵
K = torch.normal(0,1,(2,3,1,1))
Y1 = corr2d_multi_in_out_1x1(X,K)
Y2 = corr2d_multi_in_out(X,K)
# Y1结果
tensor([[[-0.3174, -0.3736, -0.3822],[-1.2920, -0.7917, -1.0706],[ 2.1018, -1.1783, 0.7724]],[[-0.4680, 3.2644, 1.2653],[ 2.7322, -0.4164, -0.0810],[-2.7743, 2.0169, -1.3969]]])
# Y2结果
tensor([[[-0.3174, -0.3736, -0.3822],[-1.2920, -0.7917, -1.0706],[ 2.1018, -1.1783, 0.7724]],[[-0.4680, 3.2644, 1.2653],[ 2.7322, -0.4164, -0.0810],[-2.7743, 2.0169, -1.3969]]])
# 当Y1与Y2的差<1e-6时继续执行,否则报错。
assert float(torch.abs(Y1-Y2).sum()) < 1e-6
补充 assert函数
一、assert函数
断言函数
二、assert 表达式:
当表达式为真时,程序继续往下执行,只是判断,不做任何处理;
当表达式为假时,抛出AssertionError错误,并将 [参数] 输出
三、用法
1、assert语句用来声明某个条件是真的。
2、如果你非常确信某个你使用的列表中至少有一个元素,而你想要检验这一点,并且在它非真的时候引发一个错误,那么assert语句是应用在这种情形下的理想语句。
3、当assert语句失败的时候,会引发一AssertionError。
相关文章:

6.4.3 1x1卷积层
特点:1x1卷积层相当于全连接层 作用:1x1卷积用于调整网络层的通道数量和控制模型复杂度 输入形状:(通道,行,列) (3,3,3) 卷积核形状:(输出通道,输入通道,行,列) (2,3,…...

[CKA]考试之检查可用节点数量
由于最新的CKA考试改版,不允许存储书签,本博客致力怎么一步步从官网把答案找到,如何修改把题做对,下面开始我们的 CKA之旅 题目为: Task 检查集群中有多少节点为Ready状态(不包括被打上 Taint࿱…...
备考错题知识点总结
错题知识点总结 强化一,错题,范围管理,128题目 1 强化练习题 1 不理解的题目 4 什么玩意? 读不懂 你正在与产品负责人一起确定可行的产品迭代计划。 当你讨论各种特性并确定它们的优先级时,你们都在努力理解哪些特…...

初识Flask:Python轻量级Web框架入门教程
Flask是一个用Python编写的轻量级Web应用框架。由于其“微”性质,Flask在提供核心服务的同时,仍然提供了许多扩展的可能性。在这篇文章中,我们将从最基础开始,学习如何使用Flask构建一个Web应用。 一、安装与初次启动 首先&…...
【BASH】回顾与知识点梳理(七)
【BASH】回顾与知识点梳理 七 七. 前六章知识点总结及练习7.1 总结7.2 练习 该系列目录 --> 【BASH】回顾与知识点梳理(目录) 七. 前六章知识点总结及练习 7.1 总结 由于核心在内存中是受保护的区块,因此我们必须要透过『 Shell 』将我…...

Python实现对IP网段的快速检测
前言 本文是该专栏的第33篇,后面会持续分享python的各种干货知识,值得关注。 在工作上可能会遇到这样的需求,需要你对某个IP地址的网段进行批量检测。将可用和不可用IP批量筛选出来,尤其是在爬虫项目中,对于IP可用性的检测需求较多。 那么在python中,有没有方法可以快速…...

伪操作、C和汇编、ATPCS协议
一、伪操作.global 全局.local 局部.equ 声明.macro 子函数.if .endif 条件编译.rept 重复操作.weak 弱化.word 申请一个字空间.byte 申请一个字节空间.align 地址对齐.arm ARM指令.thumb Thumb指令.text 代码段.data 数据段.space 申请N个字节空间 二、C和汇编的混合编程三、A…...
滤波函数+sobel边缘检测+人脸磨皮mask)
OPENCV C++(五)滤波函数+sobel边缘检测+人脸磨皮mask
滤波函数 中值滤波 medianBlur(frame, detectmat, 5); 平均滤波 blur(frame, detectmat, Size(5, 5)); 高斯滤波(最后一个是方差 越大越模糊) GaussianBlur(frame, detectmat, Size(5, 5),0); sobel的边缘检测函数 Sobel(gray, dx, CV_16S, 1, 0, 3…...

20天突破英语四级高频词汇——第②天
20天突破英语四级高频词汇~第2天加油(ง •_•)ง💪 🐳博主:命运之光 🌈专栏:英语四级高频词汇速记 🌌博主的其他文章:点击进入博主的主页 目录 20天突破英语四级高…...

【Python 学习】第一个python案例
Python的ATM机Demo 一、需要安装python环境(略) 二、ATM源码 # 初始化全局余额 money 5000# 定义初始化界面菜单函数def menu(name):"""主页面-主菜单 返回用户选择的菜单:param name: 用户名称:return: 返回菜单类型"""print(f"{name}…...

【C#学习笔记】值类型(2)
文章目录 Struct结构体类型为什么不推荐struct 元组类型可为空的值类型从可为空的值类型转换为基础类型提升的运算符如何确定可为空的值类型为什么建议少用T?装箱和取消装箱 Struct结构体类型 结构类型(“structure type”或“struct type”)是一种可封…...

【设计模式】-建造者模式
Java建造者模式:创建复杂对象的灵活构建者 在软件开发中,我们经常遇到需要创建一个复杂对象的情况。如果使用传统的构造函数进行对象创建,可能会导致构造函数参数过多,难以管理和维护。建造者模式(Builder Pattern&am…...
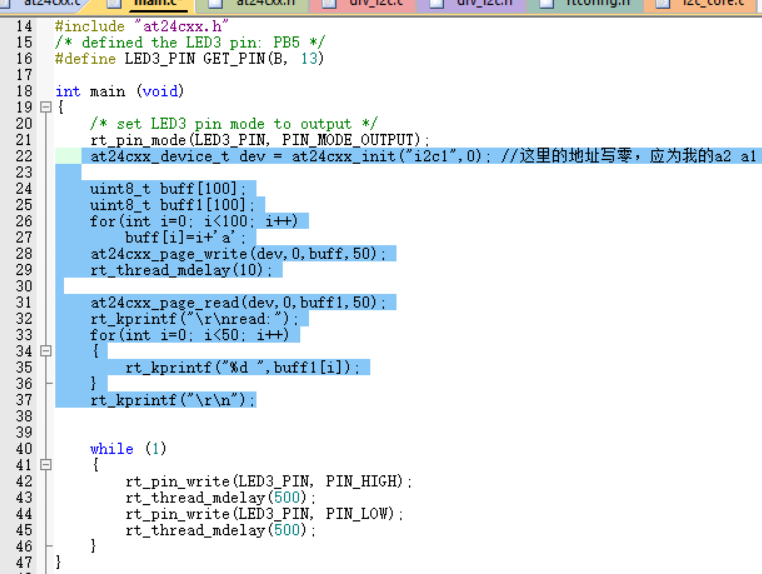
【N32L40X】学习笔记14-在RT-thread系统中读取eeprom数据
eeprom 说明 eeprom介绍 AT24C01A,1K串行EEPROM:内部组织16页8字节,1K需要一个7位数据字地址进行随机字寻址。AT24C02,2K串行EEPROM:内部组织32页8字节,2K需要一个8位数据字地址进行随机字寻址。AT24C04,4K串行EEPRO…...

Python OpenCV读取并显示USB UVC摄像头
1. 安装Python, 略。 2. 安装 OpenCV: pip install opencv-python 3. 预览摄像头画面脚本: import cv2cap cv2.VideoCapture(0, cv2.CAP_DSHOW)if not (cap.isOpened()):print("Could not open video device")cap.set(cv2.CAP_PR…...
针对高可靠性和高性能优化的1200V碳化硅沟道MOSFET
目录 标题:1200V SiC Trench-MOSFET Optimized for High Reliability and High Performance摘要信息解释研究了什么文章创新点文章的研究方法文章的结论 标题:1200V SiC Trench-MOSFET Optimized for High Reliability and High Performance 摘要 本文详…...
在服务器上搭建gitlab
最终效果展示: 官方文档: 安装部署GitLab服务 1.在服务器上下载gitlab wget https://mirrors.tuna.tsinghua.edu.cn/gitlab-ce/yum/el7/gitlab-ce-12.9.0-ce.0.el7.x86_64.rpm rpm -ivh gitlab-ce-12.9.0-ce.0.el7.x86_64.rpm 2.编辑站点位置 vim …...
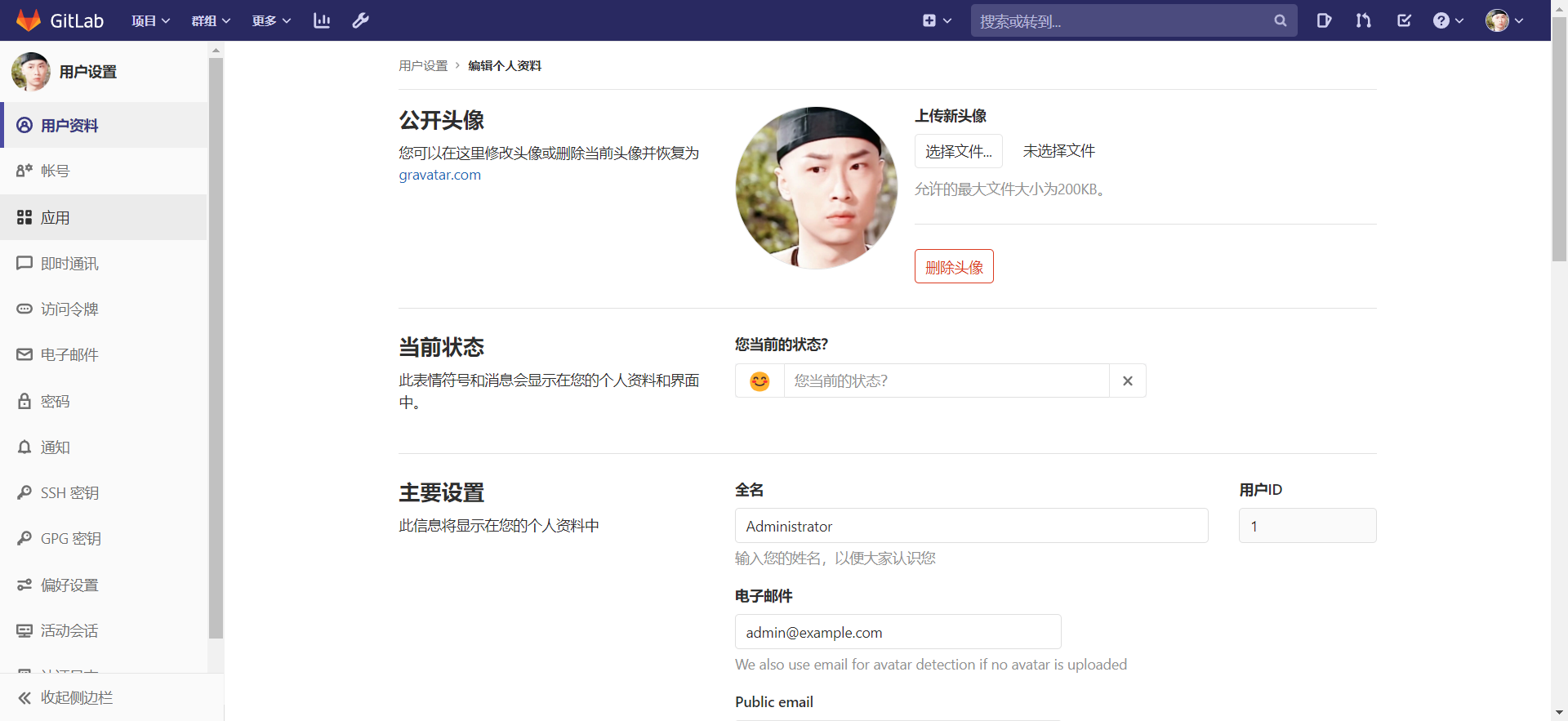
Amazon Aurora Serverless v2 正式发布:针对要求苛刻的工作负载的即时扩展
我们非常兴奋地宣布,Amazon Aurora Serverless v2 现已面向 Aurora PostgreSQL 和 MySQL 正式发布。Aurora Serverless 是一种面向 Amazon Aurora 的按需自动扩展配置,可让您的数据库根据应用程序的需求扩展或缩减容量。 亚马逊云科技开发者社区为开发者…...
nginx的优化和防盗链 重要!!!
实验一、隐藏版本号 要把nginx的版本号隐藏起来,防止恶意攻击 方法一:修改配置文件 在http模块中加入一个命令 server_token off; 过程: 备份,改配置文件一定要备份 修改配置文件 在http模块中添加 server_tokens …...
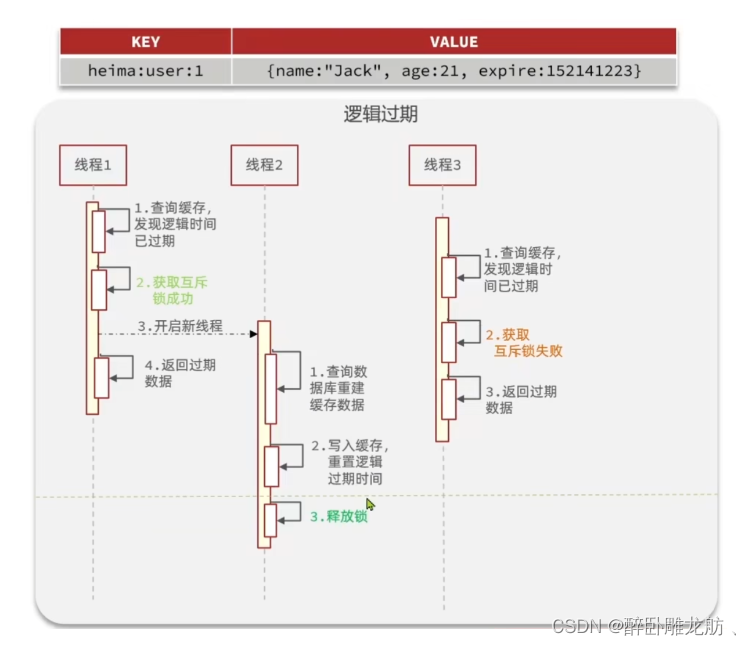
十五.redis缓存穿透,击穿,雪崩
redis哨兵模式 一.缓存穿透1.概念2.解决方案1)接口校验2)缓存空值3)布隆过滤器4)实时监控 二.缓存击穿1.概念2.解决方案1)设置热点数据永不过期2)加互斥锁3)”提前“使用互斥锁 / 逻辑过期4&…...
Spring源码——初识Spring容器
Spring源码之工厂(容器) 为什么把Spring的工厂又叫做容器呢? 工厂的责任是创建对象,但是创建完对象后还要进行存储(针对于单例的对象来讲),以供其他地方使用,这就是容器。为了能存…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...
