第三章 图论 No.5最小生成树之虚拟源点,完全图与次小生成树
文章目录
- 虚拟源点:1146. 新的开始
- 贪心或kruskal性质:1145. 北极通讯网络
- 最小生成树与完全图:346. 走廊泼水节
- 次小生成树:1148. 秘密的牛奶运输
虚拟源点:1146. 新的开始
1146. 新的开始 - AcWing题库
与一般的最小生成树问题不同,本题需要在建立电站的电井之间建立电网,在两个电站之间建立电网需要花费金额,可以看成一条具有权值的边
但是建立电网的前提是:其中一个电井需要建立电站,建立电站也需要费用
已经建立电站的两个电井之间无需建立电网,即一张电网中只需要存在一个建立电站的电井
可以将建立电站也看成具有权值的边,设置虚拟源点,在第i个电井建立电站可以转换成虚拟源点与i点之间的边,权值为建立电站的费用
此时跑个最小生成树即可
为什么不能直接跑最小生成树,再选择某个点建立一个最便宜的电站?只建立一个电站虽然能保证所有电井有电,但是两个电井建立电网的费用可能高于直接建立电站的费用
所以可能会建立多个电站,即最小生成“森林”,设置虚拟选点就是将每个森林连接,即最小生成树,此时需要跑最小生成树的算法即可
// 跑一遍最小生成树,记录其中点的最小值
#include <iostream>
#include <cstring>
using namespace std;const int N = 310;
int g[N][N], dis[N];
bool st[N];
int n;int prim()
{memset(dis, 0x3f, sizeof(dis));int res = 0;for (int i = 0; i <= n; ++ i ){int x = -1;for (int j = 0; j <= n; ++ j )if (!st[j] && (x == -1 || dis[x] > dis[j])) x = j;st[x] = true;if (i) res += dis[x];for (int y = 0; y <= n; ++ y )dis[y] = min(dis[y], g[x][y]);}return res;
}int main()
{scanf("%d", &n);for (int i = 1; i <= n; ++ i ) {scanf("%d", &g[0][i]);g[i][0] = g[0][i];}for (int i = 1; i <= n; ++i )for (int j = 1; j <= n; ++ j )scanf("%d", &g[i][j]);printf("%d\n", prim());return 0;
}
贪心或kruskal性质:1145. 北极通讯网络
1145. 北极通讯网络 - AcWing题库

三种解法,第一种,一眼想到的就是贪心:
跑个最小生成树,升序记录所有边权
若有k个卫星,选择第k大的边即可,因为k个卫星使得k个村庄可以直接通信
k-1条最大边连接的村庄用卫星,其他用发电设备通信,此时d为最大的边权
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;#define x first
#define y second
typedef pair<int, int> PII;
const int N = 510, INF = 0x3f3f3f3f;
double g[N][N], res[N];
double dis[N];
PII a[N];
bool st[N];
int n, k;double get_dis(PII a, PII b)
{int x = a.x - b.x, y = a.y - b.y;return sqrt(x * x + y * y);
}double prim()
{for (int i = 1; i <= n; ++ i ) dis[i] = INF;for (int i = 0; i < n; ++ i ){int x = -1;for (int j = 1; j <= n; ++ j )if (!st[j] && (x == -1 || dis[x] > dis[j])) x = j;st[x] = true;if (i) res[i] = dis[x];for (int y = 1; y <= n; ++ y )dis[y] = min(dis[y], g[x][y]);}sort(res + 1, res + n);return res[n - k]; // 1 ~ n-1 为最小生成树的边权升序排序
}int main()
{scanf("%d%d", &n, &k);for (int i = 1; i <= n; ++ i )scanf("%d%d", &a[i].x, &a[i].y);if (k >= n) puts("0.00");else{for (int i = 1; i <= n; ++ i )for (int j = i + 1; j <= n; ++ j )g[i][j] = g[j][i] = get_dis(a[i], a[j]);printf("%.2lf\n", prim());}return 0;
}
kurskal的性质:
每次kruskal选择当前最小边更新时,本质是在建立连通块,初始每个点各自为连通块,数量为n,每次更新连通块的数量-1,更新n-1次选择了n-1条边后,连通块的数量为1,此时最小生成树构建完成
转换题意,找到一个最小d值,删除所有大于等于d的边后,剩下的连通块数量不超过k,两个连通块中的村庄用卫星通信通信
利用kruskal的性质,更新t次后, n − t = k n-t = k n−t=k时,表示已经建立了k个连通块,这些连通块中的最大边权为答案
// 跑个最小生成树,升序记录所有边权
// 若有k个卫星,选择第k大的边即可,因为k个卫星使得k个村庄可以直接通信
// k-1个最大边连接的存在用卫星,其他用发电设备通信
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;typedef pair<int, int> PII;
const int N = 510, M = N * N / 2;
int p[N];
PII a[N];
bool st[N];
int n, k, cnt;struct Edge
{int x, y;double w;bool operator<(const Edge& e){return w < e.w;}
}edges[M];double get_dis(PII a, PII b)
{int x = a.first - b.first, y = a.second - b.second;return sqrt(x * x + y * y);
}int find(int x)
{if (x != p[x]) p[x] = find(p[x]);return p[x];
}double kruskal()
{double res;int u = 0;sort(edges, edges + cnt);for (int i = 1; i <= n; ++ i) p[i] = i;for (int i = 0; i < cnt; ++ i ){if (n - u == k) break;auto t = edges[i];int x = t.x, y = t.y;double w = t.w;x = find(x), y = find(y);if (x != y){u ++ ;res = w;p[x] = y;}}return res;
}int main()
{scanf("%d%d", &n, &k);for (int i = 1; i <= n; ++ i )scanf("%d%d", &a[i].first, &a[i].second);if (k >= n) puts("0.00");else{for (int i = 1; i <= n; ++ i )for (int j = i + 1; j <= n; ++ j )edges[cnt ++ ] = { i, j, get_dis(a[i], a[j])};printf("%.2lf\n", kruskal());}return 0;
}
debug:Edge中的w要用double存
最小生成树与完全图:346. 走廊泼水节
346. 走廊泼水节 - AcWing题库

如何合并完全图?开始时图中的每个点各自为一个集合,用集合合并的方式,保证合并后的集合为一个完全图
若集合a有x个点,b有y个点,要使得两集合合并后是个完全图(合并前两集合分别是完全图),就要将属于不同集合的点之间建一条边,总共需要建立xy条边
现在的问题是,将两个集合合并成完全图的边权为多大才能满足题意?
将树的每条边从小到大排序,每次合并当前枚举的边连接的两个集合,保证合并后的集合是一个完全图
由于要保证完全图的最小生成树唯一,所以要保证用来建立完全图的边权大于原生成树的边权
即当前枚举第i条边,这条边连接两个点 x i , y i x_i, y_i xi,yi,将 x i , y i x_i, y_i xi,yi所属的两个集合合并成完全图,需要在两个集合中的每个点之间建立一条边,并且该边的权值需要大于 w i w_i wi
#include <iostream>
#include <algorithm>
using namespace std;const int N = 6010;
struct Edge
{int x, y, w;bool operator<(const Edge& e) const {return w < e.w;}
}edges[N];
int p[N], sz[N];int find(int x)
{if (x != p[x]) p[x] = find(p[x]);return p[x];
}int main()
{int T;scanf("%d", &T);while (T -- ){int n;scanf("%d", &n);for (int i = 0; i < n - 1; ++ i )scanf("%d%d%d", &edges[i].x, &edges[i].y, &edges[i].w);sort(edges, edges + n - 1);long long res = 0;for (int i = 1; i <= n; ++ i ) p[i] = i, sz[i] = 1;for (int i = 0; i < n - 1; ++ i ){auto t = edges[i];int x = find(t.x), y = find(t.y), w = t.w;if (x != y){int n1 = sz[x], n2 = sz[y];p[x] = y;sz[y] += sz[x];res += (n1 * n2 - 1) * (w + 1);}}printf("%lld\n", res);}return 0;
}
debug:edges忘记了排序
次小生成树:1148. 秘密的牛奶运输
1148. 秘密的牛奶运输 - AcWing题库
次小生成树:

先求出最小生成树,删除最小生成树中的一条边
重复n-1次,得到的最小生成树就是次小生成树
注意:只能求出非严格次小生成树,即次小生成树的权值和可能等于最小生成树
时间复杂度 O ( m l n g m + n m ) O(mlngm + nm) O(mlngm+nm)
先求最小生成树,枚举不在树中的边,同时删除最小生成树(构成环)中的最大边,使得最终得到的图仍然是一颗树,次小生成树一定在这些树中
在生成树中任意添加一条边,必定构成环,此时需要在这个环路中删除一条边,使得该图再次成为一颗树,由于要保证权值和最小,所以要删除一条最大边
每次枚举非树边时,需要判断该边权值是否大于环的最大边,若大于则删除环中的最大值,此时能保证次小生成的权值和严格大于最小生成树
不过这种情况有一个特例,若非树边的权值等于最大边,当环中所有边的权值都等于最大边时,不更新次小生成树没有问题。若环中存在边权小于最大边的权值呢?此时可以删除这条次大的边,更新次小生成树。所以只通过判断非树边是否大于最大值将漏掉一些情况,导致少枚举次小生成树,最终导致答案的错误
因此,除了要维护两点间的最大边,还需要维护两点间的次大边,并且次大边需要严格小于最大边
若要生成非严格的次小生成树,只需要修改判断条件,在非树边的权值大于等于环的最大值时更新。多了权值相等的情况,所以删除的最大边可能和非树边权值相等,那么生成的次小生成树权值和就是相同的
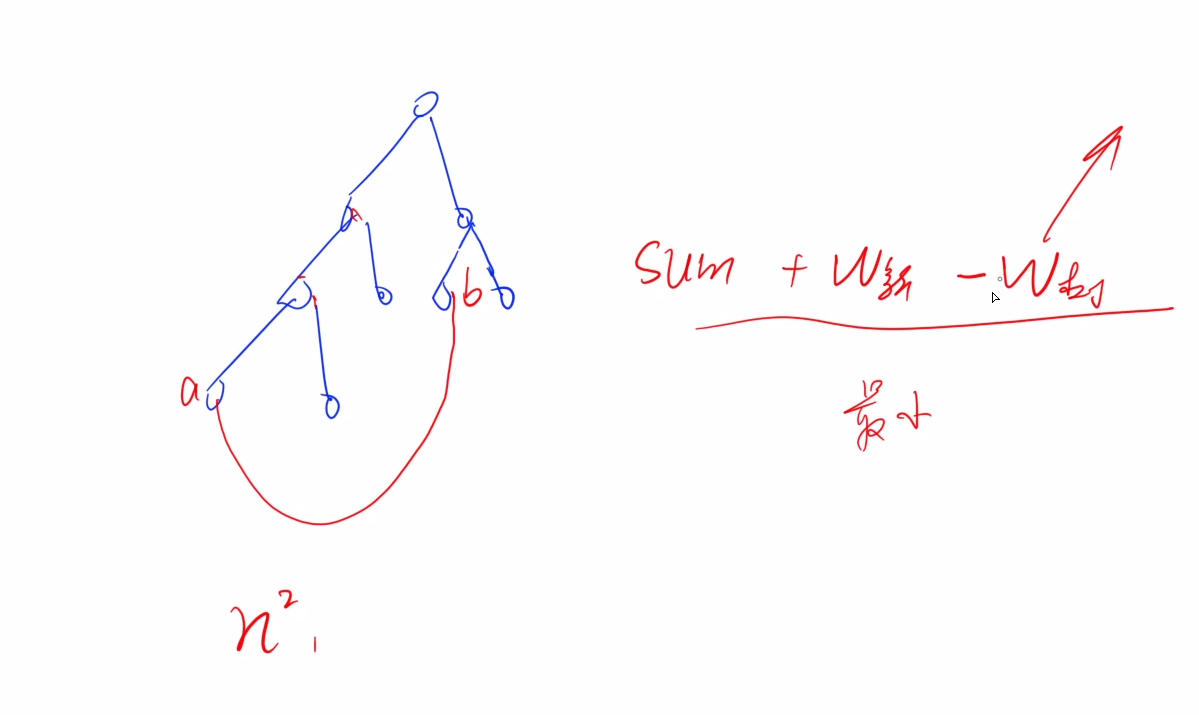
先预处理树中两点间的最大边,从根节点出发做一个dfs,每次都要 O ( n ) O(n) O(n),时间复杂度是 O ( n 2 ) O(n^2) O(n2)
总的次小生成树的时间复杂度为 O ( m l n g m + n 2 + m ) O(mlngm + n^2 + m) O(mlngm+n2+m)

由于第二种求次小生成树的方式既可以求最小生成树也能求次小生成树,所以这里实现第二种
用两个二维数组表示最小生成树中任意两点的最大边与次大边
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;typedef long long LL;
const int N = 510, M = 1e4 + 10;
struct Edge
{int x, y, w;bool f;bool operator<(const Edge& e) const {return w < e.w;}
}edges[M];int p[N];
int h[N], e[M], ne[M], w[M], idx;
int dmax1[N][N], dmax2[N][N];
int n, m;void add(int x, int y, int d)
{e[idx] = y, ne[idx] = h[x], w[idx] = d, h[x] = idx ++ ;
}int find(int x)
{if (x != p[x]) p[x] = find(p[x]);return p[x];
}// 走到x的最大边与次大边
void dfs(int x, int f, int d1, int d2, int xmax1[], int xmax2[])
{xmax1[x] = d1, xmax2[x] = d2;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (y != f){int t1 = d1, t2 = d2;if (w[i] > t1) t2 = t1, t1 = w[i];else if (w[i] < t1 && w[i] > t2) t2 = w[i];dfs(y, x, t1, t2, xmax1, xmax2);}}
}LL kruskal()
{LL sum = 0;sort(edges, edges + m);for (int i = 1; i <= n; ++ i ) p[i] = i;for (int i = 0; i < m; ++ i ){auto t = edges[i];int x = t.x, y = t.y, w = t.w;int px = find(t.x), py = find(t.y);if (px != py){sum += w;p[px] = py;add(x, y, w), add(y, x, w); // 存储最小生成树edges[i].f = true; // 树边}}return sum;
}int main()
{memset(h, -1, sizeof(h));scanf("%d%d", &n, &m);for (int i = 0; i < m; ++ i ) scanf("%d%d%d", &edges[i].x, &edges[i].y, &edges[i].w);LL sum = kruskal();for (int i = 1; i <= n; ++ i ) dfs(i, -1, -1e9, -1e9, dmax1[i], dmax2[i]);LL res = 1e19;for (int i = 0; i < m; ++ i ){if (!edges[i].f){int x = edges[i].x, y = edges[i].y, w = edges[i].w;if (w > dmax1[x][y]) res = min(res, sum - dmax1[x][y] + w);else if (w > dmax2[x][y]) res = min(res, sum - dmax2[x][y] + w);}}printf("%lld\n", res);return 0;
}
debug:构建最小生成树的同时,用邻接表存储最小生成树
auto t = edges[i];
int x = find(t.x), y = find(t.y), w = t.w;
if (x != y)
{sum += w;p[x] = y;add(x, y, w), add(y, x, w); // 存储最小生成树edges[i].f = true; // 树边
}
若这样写,构建的最小生成树是正确的,但是存储的最小生成树确实不正确的
因为x和y是边的两点所属的集合,不一定是边的两点,所以此时add无法正确保存最小生成树
相关文章:

第三章 图论 No.5最小生成树之虚拟源点,完全图与次小生成树
文章目录 虚拟源点:1146. 新的开始贪心或kruskal性质:1145. 北极通讯网络最小生成树与完全图:346. 走廊泼水节次小生成树:1148. 秘密的牛奶运输 虚拟源点:1146. 新的开始 1146. 新的开始 - AcWing题库 与一般的最小…...

RESTful API的讲解以及用PHP实现RESTful API
RESTful API是什么 RESTful是一种设计风格,是一种用于构建Web服务的架构。RESTful API是一种基于REST(Representational State Transfer)架构风格的Web服务接口设计规范。它强调使用HTTP协议中的请求方法(例如GET、POST、PUT、DEL…...

Spring中@Component和@Bean的区别
1. 用途不同 Component用于标识普通类 Bean是在配置类中声明和配置Bean对象 2. 使用方式不同 Component是一个类级别的注解,Spring通过ComponentScan注解扫描并注册为Bean. Bean是一个方法级别的注解,在配置类中手动声明和配置Bean 3. 控制权不同 Component注解修饰的类使…...

【问题解决】mysql 数据库字符串分割之后多行输出方法
背景: 项目需要从一张表查询出来数据插入到另一张表,其中有一个字段是用逗号分隔的字符串,需要多行输入到另一张表,那么这个如何实现呢 方案: 下面先粘贴下sql语句: select SUBSTRING_INDEX(SUBSTRING_…...

flutter开发实战-时间显示刚刚几分钟前几小时前
flutter开发实战-时间显示刚刚几分钟前几小时前 在开发中经常遇到从服务端获取的时间戳,需要转换显示刚刚、几分钟前、几小时前、几天前、年月日等格式。 一、代码实现 static String timeFormatterChatTimeStamp(int seconds) {try {int nowDateSeconds (DateTi…...
导出LLaMA等LLM模型为onnx
通过onnx模型可以在支持onnx推理的推理引擎上进行推理,从而可以将LLM部署在更加广泛的平台上面。此外还可以具有避免pytorch依赖,获得更好的性能等优势。 这篇博客(大模型LLaMa及周边项目(二) - 知乎)进行…...

回顾 OWASP 机器学习十大风险
日复一日,越来越多的机器学习 (ML) 模型正在开发中。机器学习模型用于查找训练数据中的模式,可以产生令人印象深刻的检测和分类能力。机器学习已经为人工智能的许多领域提供了动力,包括情感分析、图像分类、面部检测、威胁情报等。 数十亿美…...
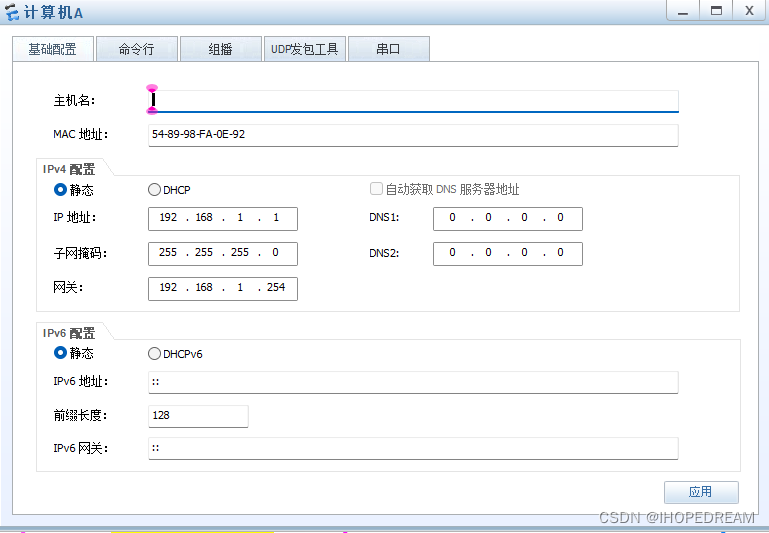
ENSP软件的基本使用命令(第三十一课)
ENSP软件的基本使用命令(第三十一课) 下面的图片是今天操作的核心基础操作 1 命令行页面 交换机 路由器 PC机 分别展示一下 页面的样子 2 基本命令结构...

五、FreeRTOS数据类型和编程规范
1、数据类型 (1)每个移植的版本都含有自己的portmacro.h头文件,里面定义了2个数据类型。 (2)TickType_t FreeRTOS配置了一个周期性的时钟中断:Tick Interrup每发生一次中断,中断次数累加,这被称为tick counttick count这个变量…...
码出高效_第二章 | 面向对象_上
目录 一. OOP理念1. 概念辨析2. 四大特性1. 抽象2. 封装3. 继承4. 多态 二. 初识Java1. JDKJDK 5-11的重要类、特性及重大改变 2. JRE关于JVM 三. 类1. 概述2. 接口和抽象类1. 概念及相同点2. 不同点3. 总结 3. 内部类4. 访问权限控制1. 由来2. public/private/无/private3. 推…...
大学生课设实训|基于springboot的在线拍卖系统
目录 项目描述 主要技术栈 功能效果 数据库设计 开发顺序 业务功能 大家好!我是龍弟-idea!需要源码资料信息可私聊我【HWL__666666】! 项目描述 本系统是一个网上商品竞拍系统,为拍卖者和竞买者提供一个在线交流平台。本项…...
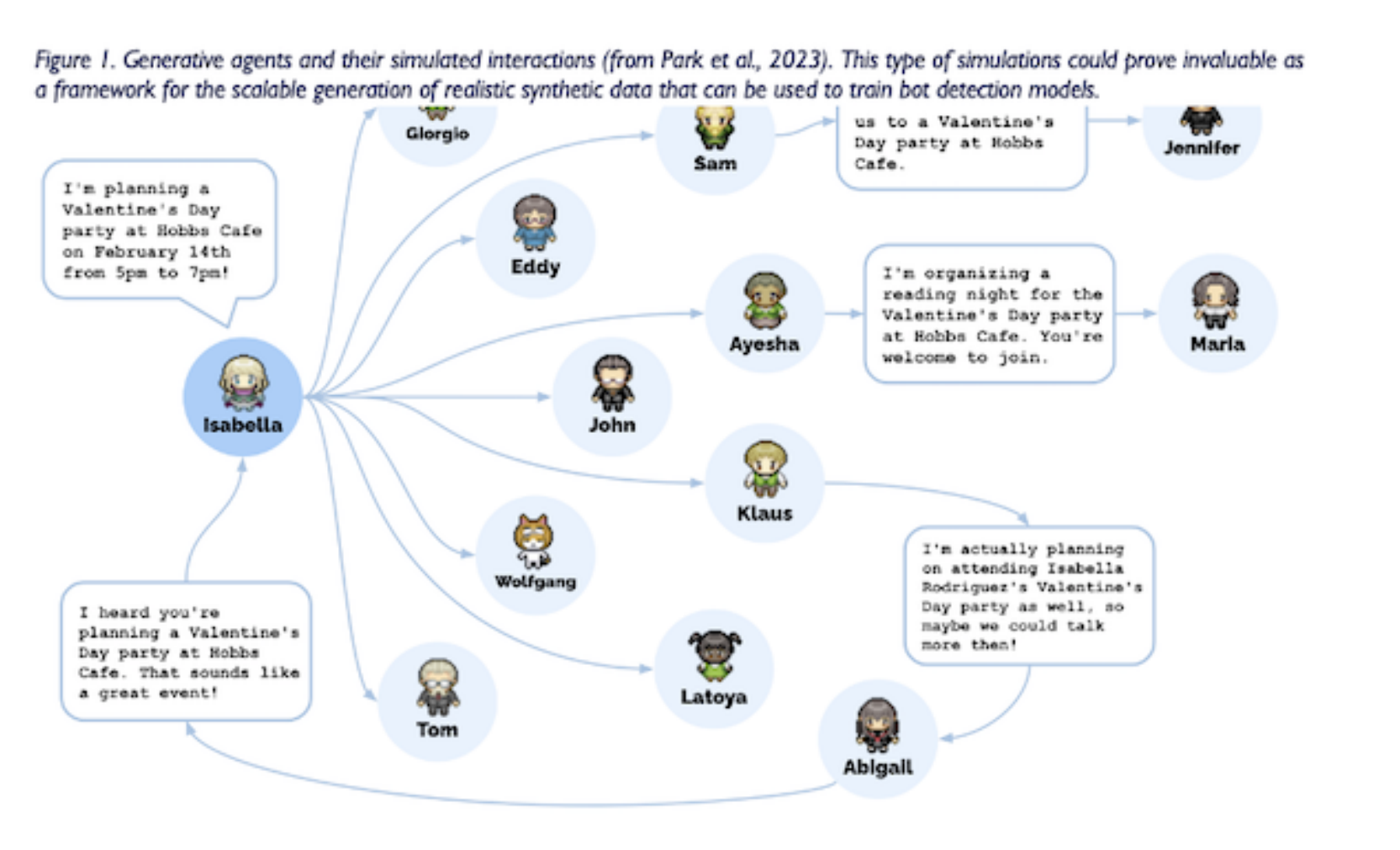
论文阅读 - Social bot detection in the age of ChatGPT: Challenges and opportunities
论文链接:https://www.researchgate.net/publication/371661341_Social_bot_detection_in_the_age_of_ChatGPT_Challenges_and_opportunities 目录 摘要: 引言 1.1. Background on social bots and their role in society 1.2. The rise of AI-gene…...
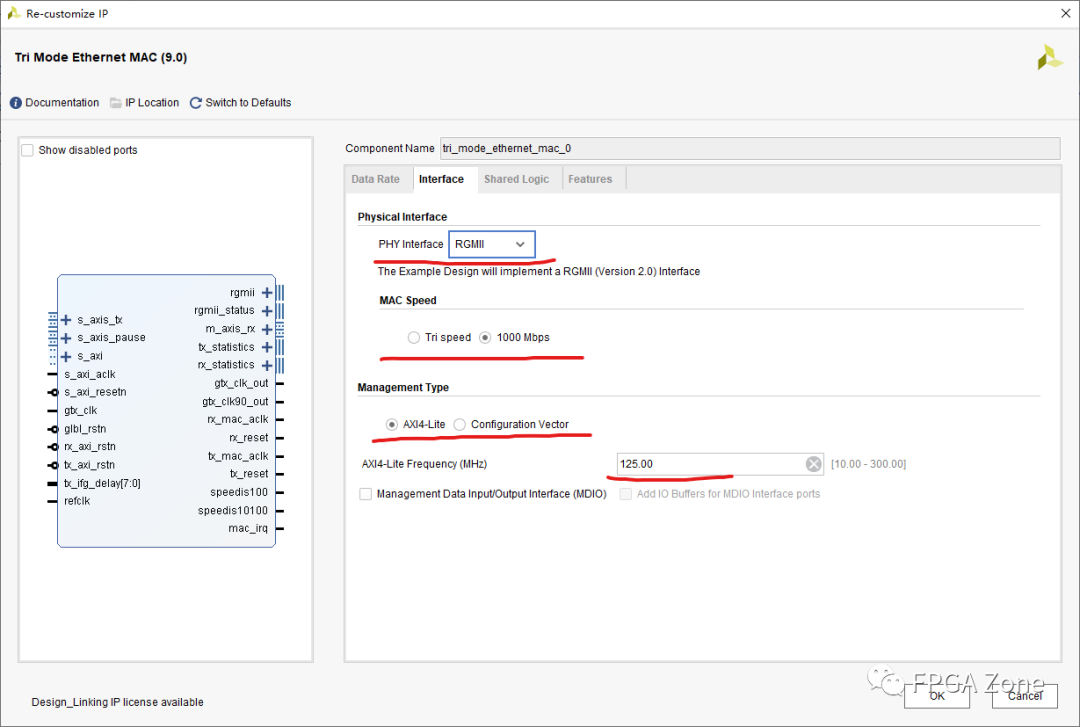
FPGA优质开源项目 - UDP RGMII千兆以太网
本文介绍一个FPGA开源项目:UDP RGMII千兆以太网通信。该项目在我之前的工作中主要是用于FPGA和电脑端之间进行图像数据传输。本文简要介绍一下该项目的千兆以太网通信方案、以太网IP核的使用以及Vivado工程源代码结构。 Vivado 的 Tri Mode Ethernet MAC IP核需要付…...
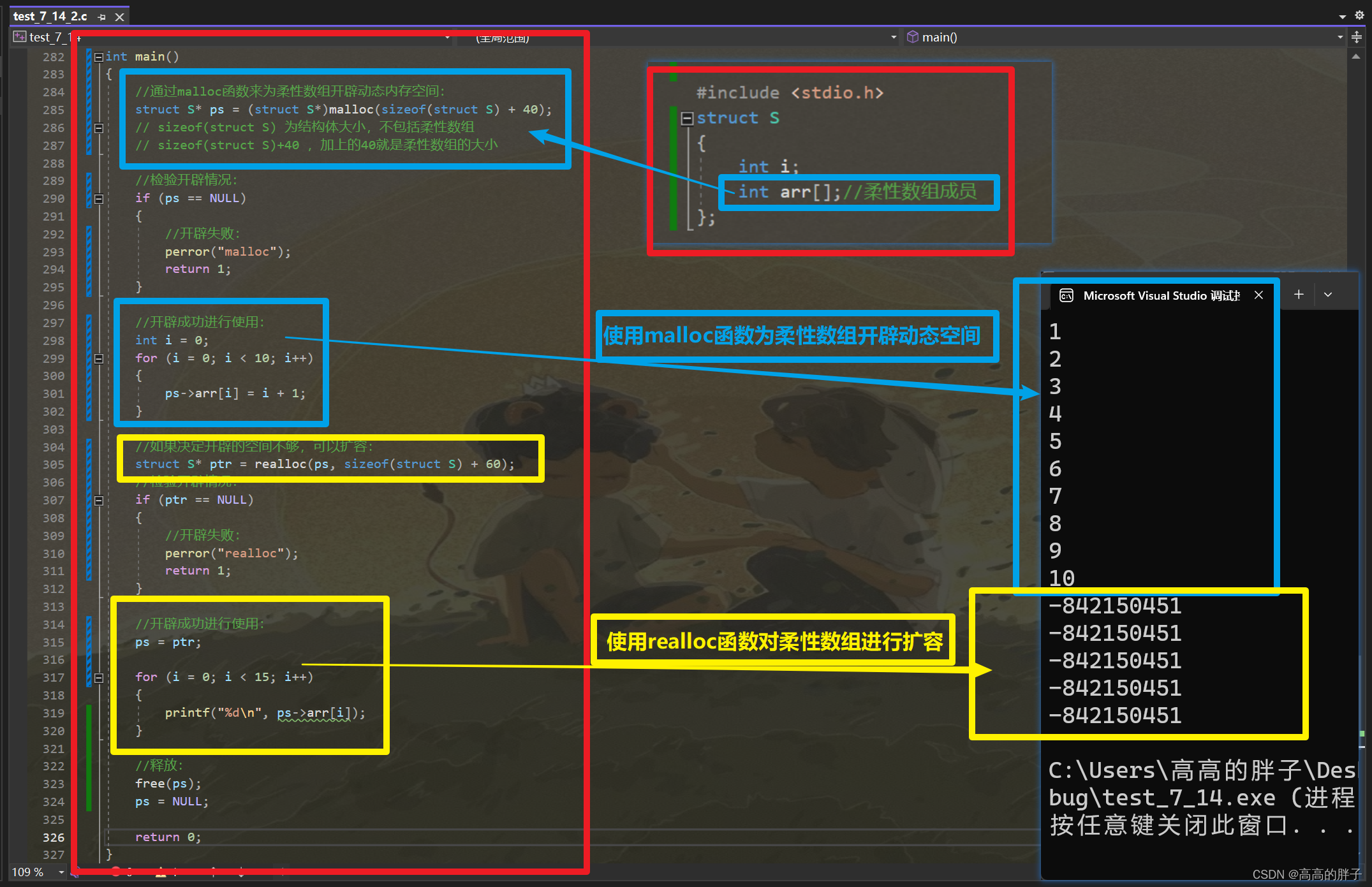
学C的第三十二天【动态内存管理】
相关代码gitee自取:C语言学习日记: 加油努力 (gitee.com) 接上期: 学C的第三十一天【通讯录的实现】_高高的胖子的博客-CSDN博客 1 . 为什么存在动态内存分配 学到现在认识的内存开辟方式有两种: 创建变量: int val …...

聊聊elasticsearch的data-streams
序 本文主要研究一下elasticsearch的data-streams data-streams 主要特性 首先data streams是由一个或者多个自动生成的隐藏索引组成的,它的格式为.ds-<data-stream>-<yyyy.MM.dd>-<generation> 示例.ds-web-server-logs-2099.03.07-000034&a…...

unreal engine c++ 创建tcp server, tcp client
TCP客户端 TcpConnect.h // Fill out your copyright notice in the Description page of Project Settings.#pragma once#include "CoreMinimal.h" #include "Common/UdpSocketReceiver.h" #include "GameFramework/Actor.h"DECLARE_DELEGATE…...
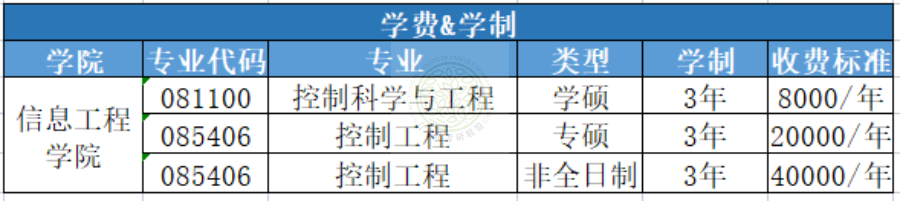
24届华东理工大学近5年自动化考研院校分析
今天给大家带来的是华东理工大学控制考研分析 满满干货~还不快快点赞收藏 一、华东理工大学 学校简介 华东理工大学原名华东化工学院,1956年被定为全国首批招收研究生的学校之一,1960年起被中共中央确定为教育部直属的全国重点大学&#…...
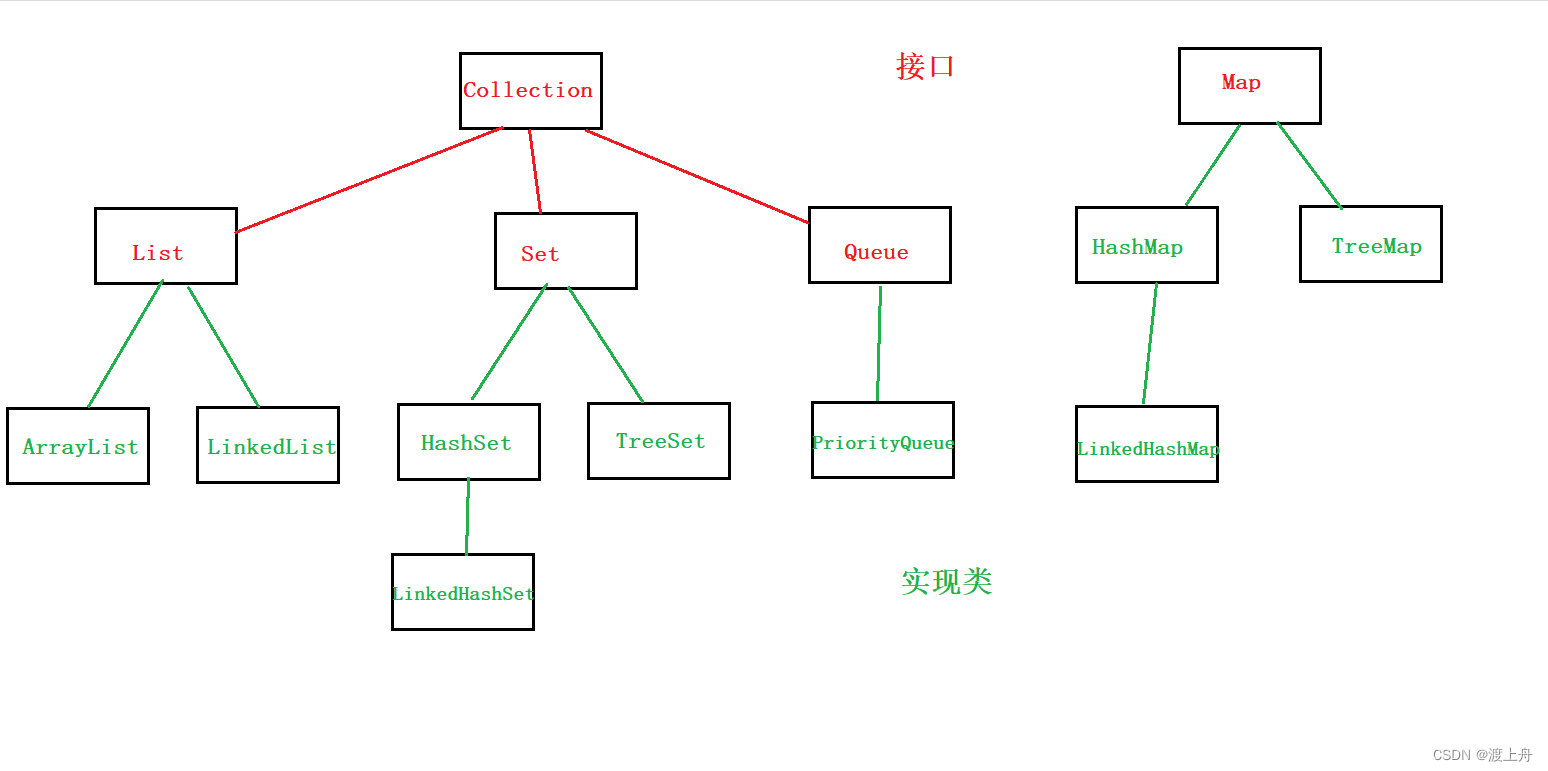
初识集合和背后的数据结构
目录 集合 Java集合框架 数据结构 算法 集合 集合,是用来存放数据的容器。其主要表现为将多个元素置于一个单元中,用于对这些元素进行增删查改。例如,一副扑克牌(一组牌的集合)、一个邮箱(一组邮件的集合)。 Java中有很多种集…...

选择适合你的数据可视化工具:提升洞察力的关键决策
导言: 在当今数据驱动的世界中,数据可视化工具成为了帮助我们理解和传达数据见解的关键工具之一。数据可视化不仅能够将复杂的数据转化为易于理解的可视化形式,还能帮助我们发现数据中的模式、趋势和关联。然而,随着市场上可视化工…...

H5中的draggable
基本语法及事件 draggable 属性规定元素是否可拖动。必须设置,否则没有拖拽效果及事件触发 提示: 链接和图像默认是可拖动的。 提示: draggable 属性经常用于拖放操作 语法 <element draggable"true|false|auto"> 值描…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...
