【Python】scipy稀疏矩阵的奇异值分解svds
文章目录
- 基本原理
- scipy实现
- 测试
基本原理
当AAA是方阵时,可以很容易地进行特征分解:A=WΣW−1A=W\Sigma W^{-1}A=WΣW−1,其中Σ\SigmaΣ是AAA的特征值组成的对角矩阵。如果WWW由标准正交基组成,则W−1=WTW^{-1}=W^TW−1=WT,特征分解可进一步写成WTΣWW^T\Sigma WWTΣW。
然而,当AAA不是方阵时,情况大不一样了,但仍然可以将AAA表示成A=UΣVTA=U\Sigma V^TA=UΣVT的形式,其中Σ\SigmaΣ也是对角矩阵,对角线上的每个元素被称作奇异值。
奇异值的求解过程和特征值息息相关,因为把AAA变成方阵很简单,只要乘以转置就行。故令L=AATL=AA^TL=AAT,R=ATAR=A^TAR=ATA,则L,RL, RL,R都可以求特征值λi\lambda_iλi和特征向量,其中LLL的特征向量为AAA的左奇异向量,RRR的特征向量为右奇异向量。对应的奇异值σi=λi\sigma_i=\sqrt{\lambda_i}σi=λi。
scipy实现
scipy.sparse.linalg中实现了稀疏矩阵奇异值分解算法,其参数列表如下
svds(A, k=6, ncv=None, tol=0, which='LM', v0=None, maxiter=None, return_singular_vectors=True, solver='arpack', random_state=None, options=None)
各参数含义如下
A待分解矩阵k奇异值个数,必须在[k,kmax][k, k_{\max}][k,kmax]之间, 当solver='propack'时,kmax=min(M,N)k_{max}=\min(M,N)kmax=min(M,N),否则kmax=min(M,N)−1k_{max}=\min(M,N)-1kmax=min(M,N)−1ncvsolver='arpack'时,此为Lanczos向量个数,否则此项忽略。tol奇异值容忍度,为0表示达到机器的精度which为'LM'时,选取最大的奇异值;'SM'则选取最小奇异值v0迭代初值maxiter迭代次数return_singular_vectors可选4个值True返回奇异向量False不返回奇异向量"u": 如果M <= N,只计算左奇异向量"vh": 如果M > N,只计算右奇异向量;如果solver='propack',这个选项将忽略矩阵维度
solver可选'arpack','propack','lobpcg',但比较吊诡的是,似乎并没有关于这三者区别的文档random_state设置随机数状态optionsdict求解器参数
其返回值有三
- u 即UUU
- s 即奇异值数组,也就是Σ\SigmaΣ的对角线
- vh 即VTV^TVT
测试
下面对奇异值分解做个测试
import numpy as np
from scipy.linalg import svd
from scipy.sparse import csc_array
from scipy.sparse.linalg import svds
np.random.seed(42) # 设置随机数状态
mat = np.random.rand(500,800)
mat[mat<0.9] = 0
csc = csc_array(mat)
u1, s1, vh1 = svds(csc, k=10)
u2, s2, vh2 = svd(mat)
结果是svds得到的结果和svd的前十个值完全相同,只是排序不一样,但也无关紧要。
下面测试一下二者的时间,由于在Windows下用不了propack,所以svds计算的奇异值数最多只能是M−1M-1M−1,也就是499,所以只能测试这个和svd返回500个奇异值的结果相比对,结果如下
>>> from timeit import timeit
>>> timeit(lambda : svds(csc, k=499), number=10)
3.651770199999987
>>> timeit(lambda : svd(mat), number=10)
0.47201400000005833
可见,稀疏矩阵在计算上的确是比不上规整的矩阵。
相关文章:

【Python】scipy稀疏矩阵的奇异值分解svds
文章目录基本原理scipy实现测试基本原理 当AAA是方阵时,可以很容易地进行特征分解:AWΣW−1AW\Sigma W^{-1}AWΣW−1,其中Σ\SigmaΣ是AAA的特征值组成的对角矩阵。如果WWW由标准正交基组成,则W−1WTW^{-1}W^TW−1WT,…...

网络安全等级保护基础知识汇总
等保 全称是网络安全等级保护,分为两个阶段 等保1.0 1994年国务院147令《中华人民共和国计算机信息系统安全保护条例》 等保2.0 2017年 网络安全法,21条规定的 国家实行网络安全等级保护制度,等保进入了有法可依阶段。 2019年国标22239-2019版…...

ros1使用过程中遇到的问题记录
Failed to fetch current robot state如果使用的是moveit助手生成的demo.launch文件启动机械臂的话,应该是其他在运行的自己写的节点代码中少了spin函数,因为getCurrentPose函数依赖于spin,也可以使用AsyncSpinner。具体看下面这个链接https:…...
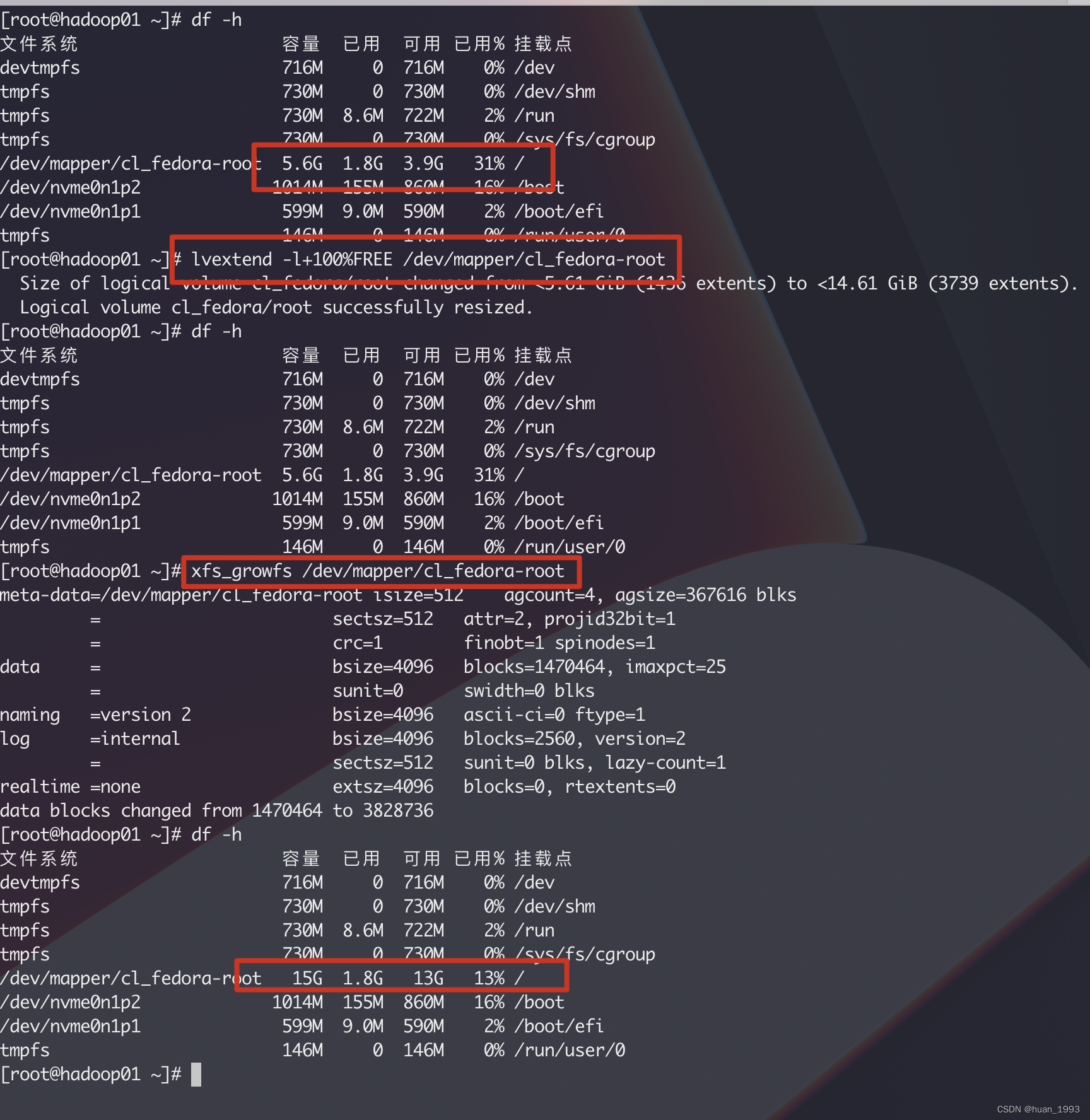
centos7给已有分区进行扩容
1、背景 最近我在虚拟机上安装软件,发现磁盘空间不足,通过上网查找资料,发现可以通过如下方法进行磁盘扩容,此处进行记录一下。 2、实现扩容 1、虚拟机上添加一个新的硬盘 2、查看我们刚刚加入的硬盘 此处我们可以看到/dev/nvm…...

package.json
{"name": "project-name", 项目名字"version": "0.1.0", 版本号"private": true, 项目包,不需要发版"scripts": { 脚本"serve": "vue-cli-service serve", 运行命令后缀是 se…...
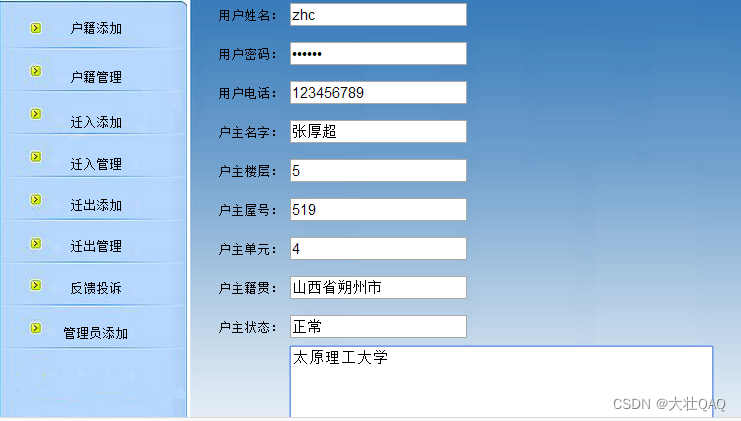
【项目精选】户籍管理系统(视频+论文+源码)
点击下载源码 当今社会人们生活质量越来越高,人们对生活品质的追求不断提升,对于孩子求学,变更住所等情况时有发生,因此对于户籍变动管理就显得十分重要,管理用户的户籍信息可以有效防止信息错乱,信息管理过…...

【IP技术】网络安全防护措施
网络安全威胁造成的形式主要包含运用系统软件缺点或侧门,运用网络防火墙安全隐患,内部结构客户的泄密、泄露和毁坏,动态口令进攻和拒绝服务式攻击等。针对该网络安全威胁,现阶段的预防措施主要有五种:1.访问控制技术&a…...
)
基于AIOT技术的智慧教室智能物联管控系统设计与实现(提纲)
摘要随着物联网技术的不断发展和智能化的不断推进,智慧教室已经成为现代教育中不可或缺的一部分。本文提出了一种基于AIOT技术的智慧教室智能物联管控系统设计与实现方案,该方案集成了物联网技术、人工智能技术、大数据技术和云计算技术等先进技术&#…...

C 指针的深造
C 指针1 关于内存那点事2 指针的概念3 指针变量的定义方法4 指针的分类5 指针和变量的关系6 指针和数组元素之间的关系7 指针数组8 指针的指针9 字符串和指针9.1 字符串的定义9.2 字符串的可修改性:9.3 初始化赋值9.4 使用时赋值9.5 字符串和指针总结10 数组指针11 …...
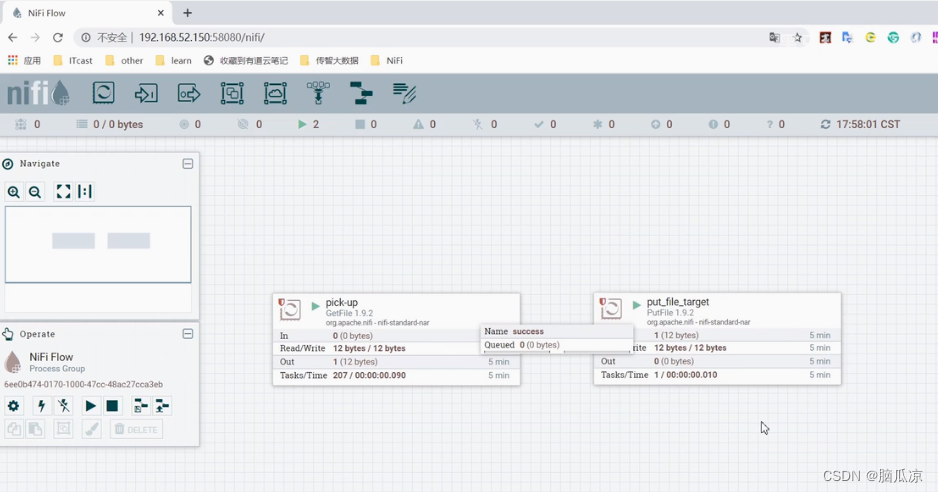
大数据之-Nifi-应用场景2-2_设置putfile处理器自动创建目标文件夹_以及存在重复文件时自动覆盖---大数据之Nifi工作笔记0006
上一节我们留了两个问题,一个是,如果我们没有创建putfile要写入的目标文件夹,会报错吗? 可以看到我们putfile目标文件夹是上面这个目录 我们来试一试,如果目标文件夹不存在,putfile处理器会自动创建吗 首先我们删除这个target目标文件夹 然后我们进入cd source目录,源文件夹目…...

buuctf Web 下
9.[ACTF2020 新生赛]Exec 访问url: http://cc3c6c27-e2df-4665-baba-1d9a32dc963e.node3.buuoj.cn/ 首页如下: 直接ping ip可以得到结果 常见管道符 1、|(就是按位或),直接执行|后面的语句 127.0.0.1 | cat /flag…...
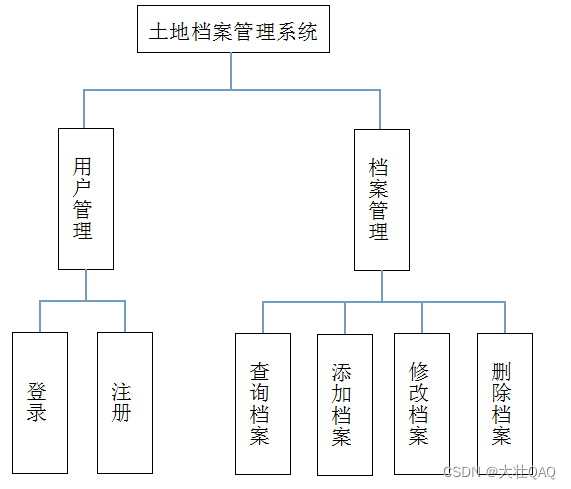
【项目精选】javaEE土地档案管理系统(源码+论文+视频)
技术:java、jsp、struts、spring、hibernate 数据库:oracle 集成开发工具:eclipse 点击下载源码 本土地项目管理系统在可行性研究的基础上,是为了进一步明确土地项目管理系统的软件需求,以便安排项目规划和进度&#x…...

JVM那些事——垃圾回收和内存分配
内存分配 默认情况下新生代和老年区的内存比例是1:2,新生代中Eden区和Survivor区的比例是8:1。 对象优先分配在Eden区。大对象直接进入老年区。通过-XX:PertenureizeThreshold参数设置临界值。长期存活的对象进入老年区。对象每熬过一次Minor GC,年龄1&…...

什么牌的运动耳机比较好、运动耳机排行榜10强
现在运动健身的潮流持续不下,而且人们长期坐于办公室办公,严重影响身体的健康,这时不论是去健身房锻炼,还是户外跑步都是非常必要的了,而蓝牙耳机作为运动必备的一款数码产品,更是受到了大家的青睐…...
)
华为OD机试题 - N 进制减法(JavaScript)
最近更新的博客 2023新华为OD机试题 - 斗地主(JavaScript)2023新华为OD机试题 - 箱子之形摆放(JavaScript)2023新华为OD机试题 - 考古学家(JavaScript)2023新华为OD机试题 - 相同数字的积木游戏 1(JavaScript)2023新华为OD机试题 - 最多等和不相交连续子序列(JavaScri…...

MyBatis 之三(查询操作 占位符#{} 与 ${}、like查询、resultMap、association、collection)
文章目录1. 参数占位符 #{} 和 ${} 的区别2. ${} 的优点3. SQL 注入问题4. like 查询5. 返回字典映射:resultMap6. 一对一查询:association7. 一对多查询:collection回顾一下,在上一篇 MyBatis 之二(增、删、改操作&am…...

【云原生之Docker实战】使用Docker部署Web在线聊天室Rocket.Chat
【云原生之Docker实战】使用Docker部署Web在线聊天室Rocket.Chat 一、Rocket.Chat介绍二、检查本地系统环境1.检查系统版本2.检查docker版本3.检查docker状态4.检查docker compose版本三、下载Rocket.Chat镜像四、部署Rocket.Chat1.创建部署目录2.编辑docker-compose.yaml文件3…...
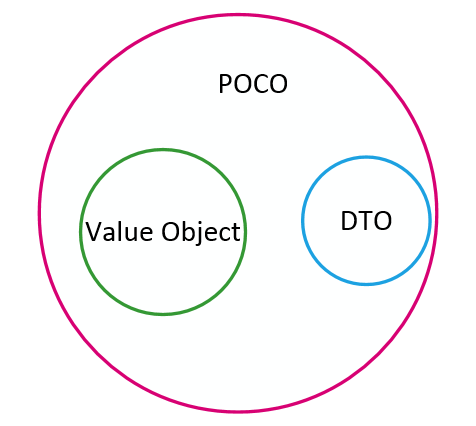
阿里一面:谈一下你对DDD的理解?2W字,帮你实现DDD自由
说在前面 在微服务的应用开发中,DDD 用得越来越普及。 在40岁老架构师 尼恩的读者交流群(50)中,DDD是一个非常、非常高频的交流话题。 最近,有小伙伴面试阿里时,遇到一个面试题: 谈谈你对DDD的理解? 小伙…...

嵌入式Linux入门级板卡的神经网络框架ncnn移植与测试-米尔i.MX6UL开发板
本篇测评由电子发烧友的优秀测评者“ALSET”提供。 米尔 MYD-Y6ULX-V2 开发板,基于 NXP i.MX6UL/i.MX6UL L处理器,该开发板被米尔称之为经典王牌产品。本次测试目标是在此开发板上进行神经网络框架ncnn的移植与测试开发,测试ncnn在此开发板上…...

扬帆优配|杠杆资金重仓股曝光,3只科创板股获多路资金青睐
到2月16日,科创板融资余额环比前一日削减1104.16万元,其间,23股融资余额环比添加超千万元,融资净买入居前的有晶科动力、诺诚健华、爱博医疗等。 到2月16日,市场融资余额算计1.48万亿元,较前一交易日削减27…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

前端工具库lodash与lodash-es区别详解
lodash 和 lodash-es 是同一工具库的两个不同版本,核心功能完全一致,主要区别在于模块化格式和优化方式,适合不同的开发环境。以下是详细对比: 1. 模块化格式 lodash 使用 CommonJS 模块格式(require/module.exports&a…...

STL 2迭代器
文章目录 1.迭代器2.输入迭代器3.输出迭代器1.插入迭代器 4.前向迭代器5.双向迭代器6.随机访问迭代器7.不同容器返回的迭代器类型1.输入 / 输出迭代器2.前向迭代器3.双向迭代器4.随机访问迭代器5.特殊迭代器适配器6.为什么 unordered_set 只提供前向迭代器? 1.迭代器…...

React、Git、计网、发展趋势等内容——前端面试宝典(字节、小红书和美团)
React React Hook实现架构、.Hook不能在循环嵌套语句中使用 , 为什么,Fiber架构,面试向面试官介绍,详细解释 用户: React Hook实现架构、.Hook不能在循环嵌套语句中使用 , 为什么,Fiber架构,面试向面试官介绍&#x…...
