EVE-NG MPLS 静态 LSP
1 拓扑
2 配置步骤
2.1 配置接口IP 和路由
LER1
interface GigabitEthernet1/0ip address 10.1.1.1 255.255.255.0quitinterface GigabitEthernet2/0ip address 11.1.1.1 255.255.255.0quitip route-static 21.1.1.0 24 10.1.1.2
VPC1
ip 11.1.1.100/24 11.1.1.1配置完成后VPC1 能够ping 通LER1 的Ge2/0
LER2
interface GigabitEthernet1/0ip address 20.1.1.2 255.255.255.0quitinterface GigabitEthernet2/0ip address 21.1.1.1 255.255.255.0quitip route-static 11.1.1.0 24 20.1.1.1
VPC2
ip 21.1.1.100/24 21.1.1.1配置完成后VPC2 能够ping 通LER2 的Ge2/0
LSR
interface GigabitEthernet1/0ip address 10.1.1.2 255.255.255.0quitinterface GigabitEthernet2/0ip address 20.1.1.1 255.255.255.0quit
2.2 使能MPLS
LER1
interface GigabitEthernet1/0mpls enablequit
LSR
interface GigabitEthernet1/0mpls enablequitinterface GigabitEthernet2/0mpls enable quitLER2
interface GigabitEthernet1/0mpls enablequit
2.3 配置LSP
LER1
static-lsp ingress 1to2 destination 21.1.1.0 24 nexthop 10.1.1.2 out-label 30
static-lsp egress 2to1 in-label 60LSR
static-lsp transit 1to2 in-label 30 nexthop 20.1.1.2 out-label 50
static-lsp transit 2to1 in-label 40 nexthop 10.1.1.1 out-label 60LER2
static-lsp egress 1to2 in-label 50
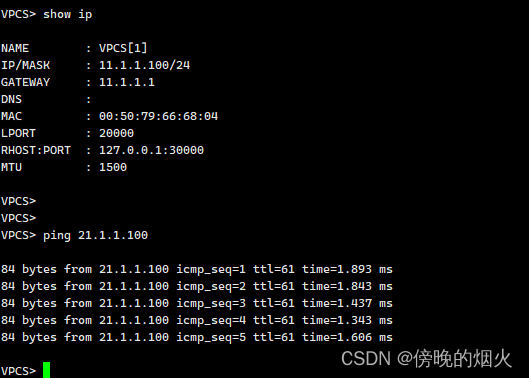
static-lsp ingress 2to1 destination 11.1.1.0 24 nexthop 20.1.1.1 out-label 402.3 在VPC上验证
相关文章：
EVE-NG MPLS 静态 LSP
1 拓扑 2 配置步骤 2.1 配置接口IP 和路由 LER1 interface GigabitEthernet1/0ip address 10.1.1.1 255.255.255.0quitinterface GigabitEthernet2/0ip address 11.1.1.1 255.255.255.0quitip route-static 21.1.1.0 24 10.1.1.2VPC1 ip 11.1.1.100/24 11.1.1.1 配置完成后…...
华秋亮相2023世界汽车制造技术暨智能装备博览会，推动汽车产业快速发展
洞悉全球汽车产业格局，前瞻业界未来趋势。2023年7月27日-30日，时隔三年，重聚武汉国际博览中心，2023世界汽车制造技术暨智能装备博览会盛大开幕。深耕汽车行业多年的世界汽车制造技术暨智能装备博览会，掀起行业热点新高…...
华为OD机试真题【开心消消乐】
1、题目描述 【开心消消乐】 给定一个N行M列的二维矩阵，矩阵中每个位置的数字取值为0或1。矩阵示例如： 1100 0001 0011 1111 现需要将矩阵中所有的1进行反转为0，规则如下： 1） 当点击一个1时，该1便被反转为…...
txt去重
目录 txt去重 让我解释一下代码的逻辑： for a in [a.strip(\n) for a in list(f_read)]: txt去重 f_read open(r./1.txt, r, encodingutf-8) f_write open(r./2.txt, w,encodingutf-8) data set() for a in [a.strip(\n) for a in list(f_read)]:if a not in …...
系统集成测试与验收
功能性测试：测试系统应提供的每一个功能和安全性限制，检查系统是否已 正常实现所有功能。 连通性测试：测试网络上任意站点间是否能够相互传输数据，测试各个终端 能否登录中心服务器，并访问数据库，对数据库…...
ElementPlus文件上传 ，在上传前钩子中判断文件是否为图片
在ElementPlus中，可以使用beforeUpload属性来指定上传文件之前的钩子函数，在该函数中可以对文件进行判断并进行相关操作。 首先，在data中定义一个isImage变量来记录文件是否为图片，初始值为false。然后，在钩子函数中判…...
涂鸦智能获Matter Non-VID Scoped PAA资质 助力开发者拥抱Matter生态
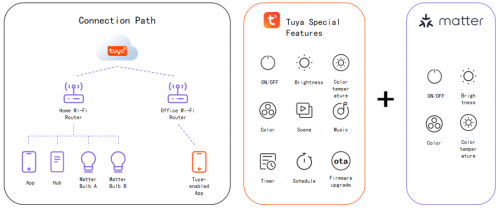
今年5月，全球化IoT开发者平台涂鸦智能（NYSE: TUYA，HKEX: 2391）正式生成Tuya Matter PAA密钥根，并于7月，成功通过了连接标准联盟和第三方MA机构审查而上线。自此，涂鸦正式成为全球同时提供支持Ma…...
nsqd的架构及源码分析
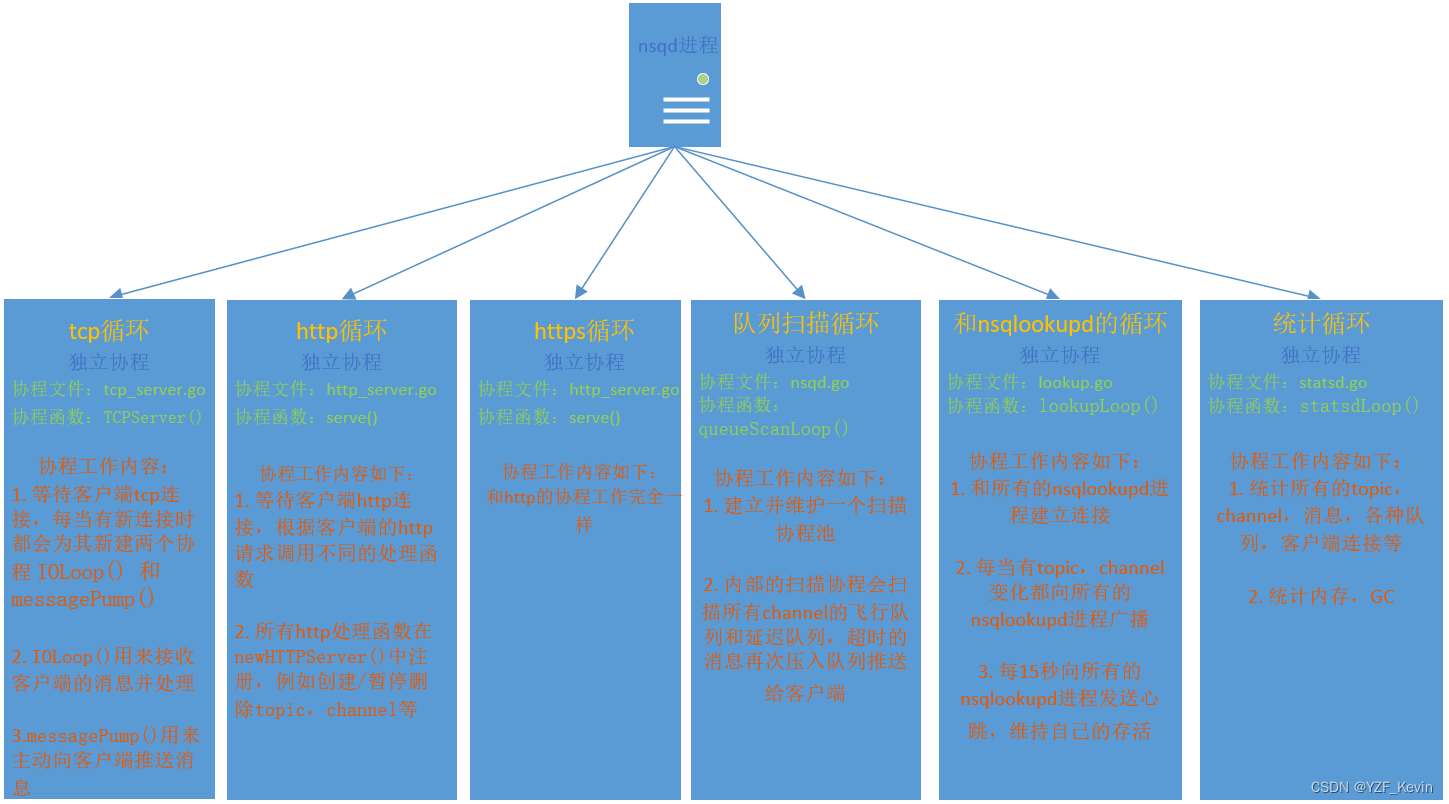
文章目录 一 nsq的整体代码结构 二 回顾nsq的整体架构图 三 nsqd进程的作用 四 nsqd启动流程的源码分析 五 本篇博客总结 在博客 nsq整体架构及各个部件作用详解_YZF_Kevin的博客-CSDN博客 中我们讲了nsq的整体框架，各个部件的大致作用。如果没看过的&…...
LeetCode解法汇总344. 反转字符串
目录链接： 力扣编程题-解法汇总_分享记录-CSDN博客 GitHub同步刷题项目： https://github.com/September26/java-algorithms 原题链接：力扣 描述： 编写一个函数，其作用是将输入的字符串反转过来。输入字符串以字符数…...
【C语言基础】数组的高级应用（上）
文章目录 一、数组的概念1.1 基本理解1.2 从内存角度理解数组1.3 从编译器角度理解数组 二、数组的定义2.1 第一种：完全初始化2.2 第二种：不完全初始化 三、访问数组的两种方式3.1 第一种：数组的方式依次访问3.2 第二种：指针的方式…...
面试题：bind、call、apply 区别？如何实现一个 bind?
面试题：bind、call、apply 区别？如何实现一个 bind? 一、call()代码描述： 二、apply()代码描述： 三、bind()—最重要代码描述： 四、call、apply、bind 总结 一、call() 代码描述： 二、apply() 代码描述&am…...
【SpringBoot学习笔记】01.第一个程序HelloWorld
项目创建方式：使用 IDEA 直接创建项目 1、创建一个新项目 2、选择spring initalizr ， 可以看到默认就是去官网的快速构建工具那里实现 3、填写项目信息 4、选择初始化的组件（初学勾选 Web 即可） 5、填写项目路径 6、等待项目…...
【学会动态规划】买卖股票的最佳时机含手续费（16）
目录 动态规划怎么学？ 1. 题目解析 2. 算法原理 1. 状态表示 2. 状态转移方程 3. 初始化 4. 填表顺序 5. 返回值 3. 代码编写 写在最后： 动态规划怎么学？ 学习一个算法没有捷径，更何况是学习动态规划， 跟我…...
网络原因导致git下载报错处理办法
如下，git clone时报错： RPC failed; curl 18 transfer closed with outstanding read data remaining 5670 bytes of body are still expected fetch-pack: unexpected disconnect while reading sideband packet early EOF fetch-pack: invalid index…...
APP后端选择什么服务器
对于很多刚入行的朋友来说，不清楚应该选择什么样的服务器提供商，是选择传统的IDC, 租用服务器租用机柜，还是选择现在很火的云服务器呢？在本文中，通过对比传统的IDC和云服务，简单阐述一下服务器的选择。 …...
什么是反射机制，反射机制的应用场景
文章目录 反射机制介绍获取 Class 对象的四种方式代码实例静态编译和动态编译反射机制优缺点反射的应用场景 反射机制介绍 JAVA 反射机制是在运行状态中，对于任意一个类，都能够知道这个类的所有属性和方法；对于任意一个对象，都能…...
Visual Studio 2019 实用功能设置（背景颜色，代码字体及行号设置）
前言 Visual Studio 2019 安装包的下载教程、安装教程 教程 博主博客链接：https://blog.csdn.net/m0_74014525 关注博主，后期持续更新系列文章 系列文章 第一篇：Visual Studio 2019 详细安装教程（图文版） 第二篇&…...
简述Mysql索引
一、索引概述 1.1 索引概述 MySQL官方对索引的定义为：索引（Index）是帮助MySQL高效获取数据的数据结构。 索引的本质：索引是数据结构。你可以简单理解为“排好序的快速查找数据结构”，满足特定查找算法。 这些数据结…...
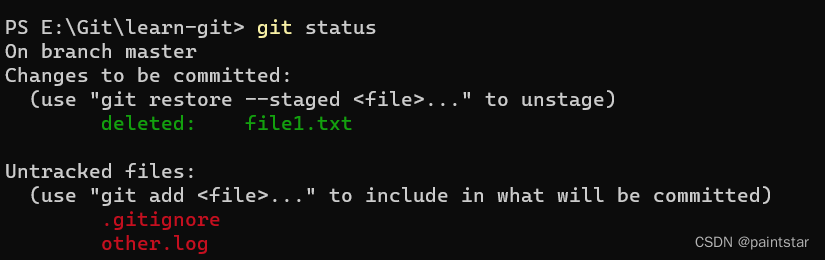
windows .gitignore 加入文件名后 依然可以从git status中看到文件问题
最近在学git，对着b站的视频操作，结果很简单的添加.gitignore文件操作，up主的正常隐藏，我的却一直出问题。 百思不得其解，网上各种啥啥啥清缓存都没讲到点上。 最后发现是.gitignore文件有问题，windows默认…...
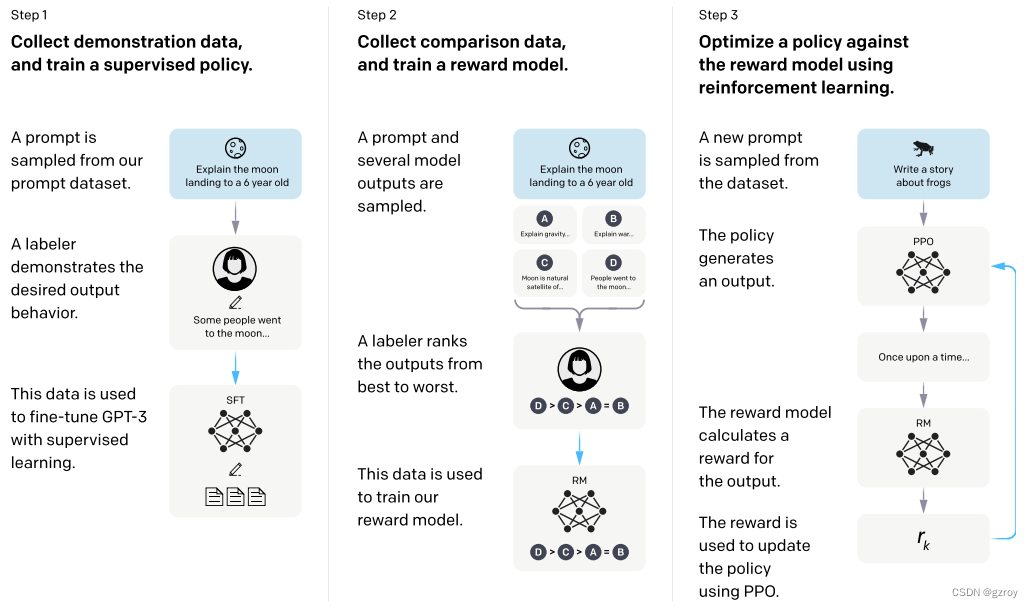
召唤神龙打造自己的ChatGPT
在之前的两篇文章中，我介绍了GPT 1和2的模型，并分别用Tensorflow和Pytorch来实现了模型的训练。具体可以见以下文章链接： 1. 基于Tensorflow来重现GPT v1模型_gzroy的博客-CSDN博客 2. 花费7元训练自己的GPT 2模型_gzroy的博客-CSDN博客 有…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下： struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...
MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能，我们需要对它的功能特点进行分析： 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具： mysql：关系型数据库&am…...
相机Camera日志实例分析之二：相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我，后续持续新增专题博文，谢谢！！！】 上一篇我们讲了： 这一篇我们开始讲： 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下： 一、场景操作步骤 操作步…...
java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中，我们会遇到使用 java 调用 dll文件 的情况，此时大概率出现UnsatisfiedLinkError链接错误，原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用，结果 dll 未实现 JNI 协…...
1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件，然后打开终端，进入下载文件夹，键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...
oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异，它们的数据同步要求既要保持数据的准确性和一致性，又要处理好性能问题。以下是一些主要的技术要点： 数据结构差异 数据类型差异ÿ…...
成都鼎讯硬核科技！雷达目标与干扰模拟器，以卓越性能制胜电磁频谱战
在现代战争中，电磁频谱已成为继陆、海、空、天之后的 “第五维战场”，雷达作为电磁频谱领域的关键装备，其干扰与抗干扰能力的较量，直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器，凭借数字射…...
【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计，提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合：各模块职责清晰，便于独立开发…...
tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录，但是由于这个树组件的节点越来越多，导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多，导致的浏览器卡顿，这里很明显就需要用到虚拟列表的技术&…...
C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj，再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...