【数理知识】协方差,随机变量的的协方差,随机变量分别是单个数字和向量时的协方差
| 序号 | 内容 |
|---|---|
| 1 | 【数理知识】自由度 degree of freedom 及自由度的计算方法 |
| 2 | 【数理知识】刚体 rigid body 及刚体的运动 |
| 3 | 【数理知识】刚体基本运动,平动,转动 |
| 4 | 【数理知识】向量数乘,内积,外积,matlab代码实现 |
| 5 | 【数理知识】协方差,随机变量的的协方差,随机变量分别是单个数字和向量时的协方差 |
| 6 | 【数理知识】已知 N>=3 个点在前后时刻的坐标,求刚体平移矩阵,旋转矩阵,且这 N>=3 点间距离始终不变代表一个刚体 |
文章目录
- 1. 马同学视频例子
- 2. 计算协方差
- 1. 计算方式一:使用期望值
- 2. 计算方式二:使用样本数据
- 3. 对比两种方式
- 3. 随机变量为二维平面的点
- 4. 随机变量为三维空间的点
- Ref
协方差是统计学中一个重要的概念,它用于衡量两个随机变量的总体误差。简单来说,协方差用于度量两个变量之间的线性关系。
如果协方差是正的,那么两个变量可能会同时增大或减小,这表明它们之间可能存在正相关的关系。
如果协方差是负的,那么其中一个变量增大时,另一个可能减小,这表明它们之间可能存在负相关的关系。
如果协方差是 0 0 0,那么两个变量可能不相关。
协方差的一个主要应用是在统计和概率理论中,用于衡量两个随机变量的联动性。此外,协方差矩阵在多元统计分析、信号处理、控制系统、投资组合优化等多个领域都有广泛的应用。
然而,协方差有一个缺点,就是它的值受到变量尺度的影响。例如,如果你测量同一个物理量,但是使用的单位不同(比如使用米和厘米),你会得到完全不同的协方差。为了克服这个问题,我们经常使用相关系数(协方差除以两个变量的标准差),这是一个标准化的协方差,不受尺度的影响,范围在-1到1之间。
接下来看协方差的推导过程。
1. 马同学视频例子
先看马同学图解数学中的视频讲解:如何通俗地解释协方差 - bilibili。我截取了几个关键步骤的视频截图。
使用的是身高 x i x_i xi 和体重 y i y_i yi 这两个指标为例子。

想要知道身高和体重的相关性,可以使用下边这种计算方式。

∑ ( x i − x ˉ ) ( y i − y ˉ ) (1) \begin{aligned} \sum (x_i - \bar{x})(y_i - \bar{y}) \end{aligned} \tag{1} ∑(xi−xˉ)(yi−yˉ)(1)
其中 x ˉ , y ˉ \bar{x}, \bar{y} xˉ,yˉ 分别表示身高,体重的平均值。
但数据差异较大时,就会出现错误判断。

这时候引入数据出现的概率 p i p_i pi,同时替换数字平均值 x ˉ , y ˉ \bar{x}, \bar{y} xˉ,yˉ 为加权平均值 μ X , μ Y \mu X, \mu Y μX,μY。
此时公式(1)变为
∑ ( x i − x ˉ ) ( y i − y ˉ ) ∑ p i ( x i − μ X ) ( y i − μ Y ) (2) \begin{aligned} &\sum (x_i - \bar{x})(y_i - \bar{y}) \\ &\sum p_i (x_i - \mu X)(y_i - \mu Y) \end{aligned} \tag{2} ∑(xi−xˉ)(yi−yˉ)∑pi(xi−μX)(yi−μY)(2)
其中 μ X , μ Y \mu X, \mu Y μX,μY 表示加权平均, p i p_i pi 表示每一项的概率。

最后,将式子改写成期望的形式有
∑ ( x i − x ˉ ) ( y i − y ˉ ) ∑ p i ( x i − μ X ) ( y i − μ Y ) Cov ( X , Y ) = E [ ( X − μ X ) ( Y − μ Y ) ] (3) \begin{aligned} &\sum (x_i - \bar{x})(y_i - \bar{y}) \\ &\sum p_i (x_i - \mu X)(y_i - \mu Y) \\ \text{Cov} (X,Y) &= \text{E} [(X-\mu X)(Y-\mu Y)] \end{aligned} \tag{3} Cov(X,Y)∑(xi−xˉ)(yi−yˉ)∑pi(xi−μX)(yi−μY)=E[(X−μX)(Y−μY)](3)
2. 计算协方差
总的来说,计算协方差可以使用两种方式。区别在于是否知道全部的数据量,也就是说我们是知道随机变量的期望均值,还是仅知道样本数据的样本均值。至于期望均值和样本均值的区别,请查阅文章:【LinearAlgebra】12.1 Mean, Variance, and Probability。
第一种,当我们知道所有的数据(总数据量为 N N N)时,也就是知道了具体的期望值,可以使用公式
Cov ( X , Y ) = E [ ( X − μ X ) ( Y − μ Y ) ] \begin{aligned} \text{Cov} (X,Y) &= \text{E} [(X-\mu X)(Y-\mu Y)] \end{aligned} Cov(X,Y)=E[(X−μX)(Y−μY)]
来计算。其中 μ X 、 μ Y \mu X、\mu Y μX、μY 分别是 X X X 和 Y Y Y 的期望值。
第二种是仅知道样本数据(样本数量为 n n n,总数据量为 N N N)时,可以使用公式
Cov ( X , Y ) = ∑ i n ( x i − x ˉ ) ( y i − y ˉ ) n − 1 \begin{aligned} \text{Cov} (X,Y) &= \frac{\sum_i^n (x_i - \bar{x})(y_i - \bar{y})}{n-1} \end{aligned} Cov(X,Y)=n−1∑in(xi−xˉ)(yi−yˉ)
来估算(注意不是计算)协方差。其中 x i 、 y i x_i、y_i xi、yi 是两个随机变量已知的样本数据, x ˉ 、 y ˉ \bar{x}、\bar{y} xˉ、yˉ 是两个随机变量的平均值。注意这里是除以( n − 1 n-1 n−1)而不是 n n n,因为这是无偏估计,当样本数据用来估计总计参数时,需要这样处理。
接下来用同一组数据,分别使用两种方式来计算协方差,看下效果。
1. 计算方式一:使用期望值
假设有两个随机变量 X = { 1 , 2 , 2 , 2 , 3 } X = \{1, 2, 2, 2, 3\} X={1,2,2,2,3}, Y = { 6 , 6 , 7 , 7 , 8 } Y = \{6, 6, 7, 7, 8\} Y={6,6,7,7,8}。我们能够分别计算二者的期望均值为
μ X = ( 1 + 2 + 2 + 2 + 3 ) / 5 = 2 μ Y = ( 6 + 6 + 7 + 7 + 8 ) / 5 = 6.8 \begin{aligned} \mu X &= (1+2+2+2+3)/5=2 \\ \mu Y &= (6+6+7+7+8)/5=6.8 \end{aligned} μXμY=(1+2+2+2+3)/5=2=(6+6+7+7+8)/5=6.8
那么协方差为
Cov ( X , Y ) = E [ ( X − μ X ) ( Y − μ Y ) ] = [ ( 1 − 2 ) ( 6 − 6.8 ) + ( 2 − 2 ) ( 6 − 6.8 ) + ( 2 − 2 ) ( 7 − 6.8 ) + ( 2 − 2 ) ( 7 − 6.8 ) + ( 3 − 2 ) ( 8 − 6.8 ) ] / 5 = [ 0.8 + 0 + 0 + 0 + 1.2 ] / 5 = 0.4 \begin{aligned} \text{Cov} (X,Y) &= \text{E} [(X-\mu X)(Y-\mu Y)] \\ &= [(1-2)(6-6.8) + (2-2)(6-6.8) + (2-2)(7-6.8) + (2-2)(7-6.8) + (3-2)(8-6.8)] / 5 \\ &= [0.8 + 0 + 0 + 0 + 1.2] / 5 \\ &= 0.4 \end{aligned} Cov(X,Y)=E[(X−μX)(Y−μY)]=[(1−2)(6−6.8)+(2−2)(6−6.8)+(2−2)(7−6.8)+(2−2)(7−6.8)+(3−2)(8−6.8)]/5=[0.8+0+0+0+1.2]/5=0.4
所以,这两个随机变量的协方差为 0.4 0.4 0.4。
2. 计算方式二:使用样本数据
还是上边的两个随机变量。但假如我们仅知道其中的 3 3 3 个,如 X = { 1 , 2 , 2 , 3 } X = \{1, 2, 2, 3\} X={1,2,2,3}, Y = { 6 , 6 , 7 , 8 } Y = \{6, 6, 7, 8\} Y={6,6,7,8},同时也不知道每个样本的概率。这时候,我们仅能计算出来样本均值,也就是
x ˉ = ( 1 + 2 + 2 + 3 ) / 4 = 2 y ˉ = ( 6 + 6 + 7 + 8 ) / 4 = 6.75 \begin{aligned} \bar{x} &= (1+2+2+3)/4=2 \\ \bar{y} &= (6+6+7+8)/4=6.75 \end{aligned} xˉyˉ=(1+2+2+3)/4=2=(6+6+7+8)/4=6.75
那么协方差为
Cov ( X , Y ) = ∑ i n ( x i − x ˉ ) ( y i − y ˉ ) n − 1 = [ ( 1 − 2 ) ( 6 − 6.75 ) + ( 2 − 2 ) ( 6 − 6.75 ) + ( 2 − 2 ) ( 7 − 6.75 ) + ( 3 − 2 ) ( 8 − 6.75 ) ] / ( 4 − 1 ) = [ 0.75 + 0 + 0 + 1.25 ] / 3 = 0.6667 \begin{aligned} \text{Cov} (X,Y) &= \frac{\sum_i^n (x_i - \bar{x})(y_i - \bar{y})}{n-1} \\ &= [(1-2)(6-6.75) + (2-2)(6-6.75) + (2-2)(7-6.75) + (3-2)(8-6.75)] / (4-1) \\ &= [0.75 + 0 + 0 + 1.25] / 3 \\ &= 0.6667 \end{aligned} Cov(X,Y)=n−1∑in(xi−xˉ)(yi−yˉ)=[(1−2)(6−6.75)+(2−2)(6−6.75)+(2−2)(7−6.75)+(3−2)(8−6.75)]/(4−1)=[0.75+0+0+1.25]/3=0.6667
所以,用这一组样本估算出来的协方差为 0.6667 0.6667 0.6667。
在上述样本的基础上,假如我们知道了其概率,也就是样本为 X = { 1 , 2 , 2 , 3 } X = \{1, 2, 2, 3\} X={1,2,2,3}, Y = { 6 , 6 , 7 , 8 } Y = \{6, 6, 7, 8\} Y={6,6,7,8},同时每个样本的概率为 P = { 0.2 , 0.2 , 0.4 , 0.2 } P = \{0.2, 0.2, 0.4, 0.2\} P={0.2,0.2,0.4,0.2}。那此时就可以计算出来随机变量的期望值为
μ X = 0.2 ∗ 1 + 0.2 ∗ 2 + 0.4 ∗ 2 + 0.2 ∗ 3 = 2 μ Y = 0.2 ∗ 6 + 0.2 ∗ 6 + 0.4 ∗ 7 + 0.2 ∗ 8 = 6.8 \begin{aligned} \mu X &= 0.2*1+0.2*2+0.4*2+0.2*3=2 \\ \mu Y &= 0.2*6+0.2*6+0.4*7+0.2*8=6.8 \end{aligned} μXμY=0.2∗1+0.2∗2+0.4∗2+0.2∗3=2=0.2∗6+0.2∗6+0.4∗7+0.2∗8=6.8
计算协方差为
Cov ( X , Y ) = ∑ p i ( x i − μ X ) ( y i − μ Y ) = 0.2 ∗ ( 1 − 2 ) ( 6 − 8 ) + 0.2 ∗ ( 2 − 2 ) ( 6 − 8 ) + 0.4 ∗ ( 2 − 2 ) ( 7 − 8 ) + 0.2 ∗ ( 3 − 2 ) ( 8 − 8 ) = 0.2 ∗ ( 2 ) + 0.2 ∗ ( 0 ) + 0.4 ∗ ( 0 ) + 0.2 ∗ ( 0 ) = 0.4 \begin{aligned} \text{Cov} (X,Y) &= \sum p_i (x_i - \mu X)(y_i - \mu Y) \\ &= 0.2*(1-2)(6-8) + 0.2*(2-2)(6-8) + 0.4*(2-2)(7-8) + 0.2*(3-2)(8-8) \\ &= 0.2*(2) + 0.2*(0) + 0.4*(0) + 0.2*(0) \\ &= 0.4 \end{aligned} Cov(X,Y)=∑pi(xi−μX)(yi−μY)=0.2∗(1−2)(6−8)+0.2∗(2−2)(6−8)+0.4∗(2−2)(7−8)+0.2∗(3−2)(8−8)=0.2∗(2)+0.2∗(0)+0.4∗(0)+0.2∗(0)=0.4
3. 对比两种方式
至于为什么知道了样本的概率就能知道精准知道协方差了,可以看一下数据的排列。
首先,全部数据可以排列成
Data N = [ x i 1 2 2 2 3 y i 6 6 7 7 8 p i 0.2 0.2 0.2 0.2 0.2 ] = [ x i 1 2 2 3 y i 6 6 7 8 p i 0.2 0.2 0.4 0.2 ] \text{Data}_N = \left[\begin{matrix} x_i & 1 & 2 & 2 & 2 & 3 \\ y_i & 6 & 6 & 7 & 7 & 8 \\ p_i & 0.2 & 0.2 & 0.2 & 0.2 & 0.2 \\ \end{matrix}\right] =\left[\begin{matrix} x_i & 1 & 2 & 2 & 3 \\ y_i & 6 & 6 & 7 & 8 \\ p_i & 0.2 & 0.2 & 0.4 & 0.2 \\ \end{matrix}\right] DataN= xiyipi160.2260.2270.2270.2380.2 = xiyipi160.2260.2270.4380.2
而使用样本估算的方法时,我们用的应该是
Data n = [ x i 1 2 2 3 y i 6 6 7 8 p i 0.25 0.25 0.25 0.25 ] \text{Data}_n = \left[\begin{matrix} x_i & 1 & 2 & 2 & 3 \\ y_i & 6 & 6 & 7 & 8 \\ p_i & 0.25 & 0.25 & 0.25 & 0.25 \\ \end{matrix}\right] Datan= xiyipi160.25260.25270.25380.25
所以,对比观看一下可以知道,我们在样本估算时,实际也是假设了每个样本出现的概率都是相同的。
3. 随机变量为二维平面的点
在上述描述中,我们随机变量中的样本都是数字,也就是每个样本数据的维度都是 1 1 1 维的。接下来假设样本为二维平面中的点,也就是样本数据的维度为 2 2 2 维。
假设随机变量的样本为: X = { ( 1 , 2 ) , ( 3 , 4 ) , ( 5 , 6 ) } X = \{(1,2), (3,4), (5,6)\} X={(1,2),(3,4),(5,6)}, Y = { ( 2 , 3 ) , ( 4 , 5 ) , ( 6 , 7 ) } Y = \{(2,3), (4,5), (6,7)\} Y={(2,3),(4,5),(6,7)}。首先计算均值为
x ˉ = ( 1 + 3 + 5 , 2 + 4 + 6 ) / 3 = ( 3 , 4 ) y ˉ = ( 2 + 4 + 6 , 3 + 5 + 7 ) / 3 = ( 4 , 5 ) \begin{aligned} \bar{x} &= (1+3+5, 2+4+6)/3=(3,4) \\ \bar{y} &= (2+4+6, 3+5+7)/3=(4,5) \end{aligned} xˉyˉ=(1+3+5,2+4+6)/3=(3,4)=(2+4+6,3+5+7)/3=(4,5)
然后,我们计算协方差矩阵。在这种情况下,协方差矩阵是一个 2 × 2 2 \times 2 2×2 的矩阵,其每个元素 Cov ( X , Y ) i j \text{Cov}(X,Y)_{ij} Cov(X,Y)ij 是 X X X 的第 i i i 个维度和 Y Y Y 的第 j j j 个维度的协方差。在这种情况下,我们计算的是 X X X 和 Y Y Y 之间的协方差,而不是 X X X 和 Y Y Y 内部的协方差,所以我们是在计算 X X X 的第 i i i 个维度和 Y Y Y 的第 j j j 个维度。
矩阵的每一个元素 ( i , j ) (i,j) (i,j) 都是通过以下公式计算得到的:
Cov ( X , Y ) i j = ∑ k n = 3 ( x k i − x ˉ i ) ( y k j − y ˉ i ) n − 1 \begin{aligned} \text{Cov} (X,Y)_{ij} &= \frac{\sum_k^{n=3} (x_{ki} - \bar{x}_i)(y_{kj} - \bar{y}_i)}{n-1} \end{aligned} Cov(X,Y)ij=n−1∑kn=3(xki−xˉi)(ykj−yˉi)
其中 x k i x_{ki} xki 表示第 k k k 个样本的第 i i i 个维度的值, x ˉ i \bar{x}_i xˉi 表示均值的第 i i i 个维度。
依次代入数值并展开有
Cov ( X , Y ) i = 1 , j = 1 = ( 1 − 3 ) ( 2 − 4 ) + ( 3 − 3 ) ( 4 − 4 ) + ( 5 − 3 ) ( 6 − 4 ) 3 − 1 = 4 Cov ( X , Y ) i = 1 , j = 2 = ( 1 − 3 ) ( 3 − 5 ) + ( 3 − 3 ) ( 5 − 5 ) + ( 5 − 3 ) ( 7 − 5 ) 3 − 1 = 4 \begin{aligned} \text{Cov} (X,Y)_{i=1,j=1} &= \frac{(1-3)(2-4) + (3-3)(4-4) + (5-3)(6-4)}{3-1} = 4 \\ \text{Cov} (X,Y)_{i=1,j=2} &= \frac{(1-3)(3-5) + (3-3)(5-5) + (5-3)(7-5)}{3-1} = 4 \end{aligned} Cov(X,Y)i=1,j=1Cov(X,Y)i=1,j=2=3−1(1−3)(2−4)+(3−3)(4−4)+(5−3)(6−4)=4=3−1(1−3)(3−5)+(3−3)(5−5)+(5−3)(7−5)=4
Cov ( X , Y ) i = 2 , j = 1 = ( 2 − 4 ) ( 2 − 4 ) + ( 4 − 4 ) ( 4 − 4 ) + ( 6 − 4 ) ( 6 − 4 ) 3 − 1 = 4 Cov ( X , Y ) i = 2 , j = 2 = ( 2 − 4 ) ( 3 − 5 ) + ( 4 − 4 ) ( 5 − 5 ) + ( 6 − 4 ) ( 7 − 5 ) 3 − 1 = 4 \begin{aligned} \text{Cov} (X,Y)_{i=2,j=1} &= \frac{(2-4)(2-4) + (4-4)(4-4) + (6-4)(6-4)}{3-1} = 4 \\ \text{Cov} (X,Y)_{i=2,j=2} &= \frac{(2-4)(3-5) + (4-4)(5-5) + (6-4)(7-5)}{3-1} = 4 \end{aligned} Cov(X,Y)i=2,j=1Cov(X,Y)i=2,j=2=3−1(2−4)(2−4)+(4−4)(4−4)+(6−4)(6−4)=4=3−1(2−4)(3−5)+(4−4)(5−5)+(6−4)(7−5)=4
故协方差矩阵为
Cov ( X , Y ) = [ 4 4 4 4 ] \begin{aligned} \text{Cov} (X,Y) &= \left[\begin{matrix} 4 & 4 \\ 4 & 4 \\ \end{matrix}\right] \end{aligned} Cov(X,Y)=[4444]
4. 随机变量为三维空间的点
接下来假设样本为三维空间中的点,也就是样本数据的维度为 3 3 3 维。
假设随机变量的样本为: X = { ( 1 , 2 , 3 ) , ( 4 , 5 , 6 ) , ( 7 , 8 , 9 ) } X = \{(1,2,3), (4,5,6), (7,8,9)\} X={(1,2,3),(4,5,6),(7,8,9)}, Y = { ( 2 , 3 , 4 ) , ( 5 , 6 , 7 ) , ( 8 , 9 , 10 ) } Y = \{(2,3,4), (5,6,7), (8,9,10)\} Y={(2,3,4),(5,6,7),(8,9,10)}。首先计算均值为
x ˉ = ( 1 + 4 + 7 , 2 + 5 + 8 , 3 + 6 + 9 ) / 3 = ( 4 , 5 , 6 ) y ˉ = ( 2 + 5 + 8 , 3 + 6 + 9 , 4 + 7 + 10 ) / 3 = ( 5 , 6 , 7 ) \begin{aligned} \bar{x} &= (1+4+7, 2+5+8, 3+6+9)/3=(4, 5, 6) \\ \bar{y} &= (2+5+8, 3+6+9, 4+7+10)/3=(5, 6, 7) \end{aligned} xˉyˉ=(1+4+7,2+5+8,3+6+9)/3=(4,5,6)=(2+5+8,3+6+9,4+7+10)/3=(5,6,7)
然后,我们计算协方差矩阵。在这种情况下,协方差矩阵是一个 3 × 3 3 \times 3 3×3 的矩阵,其每个元素 Cov ( X , Y ) i j \text{Cov}(X,Y)_{ij} Cov(X,Y)ij 是 X X X 的第 i i i 个维度和 Y Y Y 的第 j j j 个维度的协方差。
矩阵的每一个元素 ( i , j ) (i,j) (i,j) 都是通过以下公式计算得到的:
Cov ( X , Y ) i j = ∑ k n = 3 ( x k i − x ˉ i ) ( y k j − y ˉ i ) n − 1 \begin{aligned} \text{Cov} (X,Y)_{ij} &= \frac{\sum_k^{n=3} (x_{ki} - \bar{x}_i)(y_{kj} - \bar{y}_i)}{n-1} \end{aligned} Cov(X,Y)ij=n−1∑kn=3(xki−xˉi)(ykj−yˉi)
依次代入数值并展开有
Cov ( X , Y ) i = 1 , j = 1 = ( 1 − 4 ) ( 2 − 5 ) + ( 4 − 4 ) ( 3 − 5 ) + ( 7 − 4 ) ( 4 − 5 ) 3 − 1 = 3 Cov ( X , Y ) i = 1 , j = 2 = ( 1 − 4 ) ( 5 − 6 ) + ( 4 − 4 ) ( 6 − 6 ) + ( 7 − 4 ) ( 7 − 6 ) 3 − 1 = 3 Cov ( X , Y ) i = 1 , j = 3 = ( 1 − 4 ) ( 8 − 7 ) + ( 4 − 4 ) ( 9 − 7 ) + ( 7 − 4 ) ( 10 − 7 ) 3 − 1 = 3 \begin{aligned} \text{Cov} (X,Y)_{i=1,j=1} &= \frac{(1-4)(2-5) + (4-4)(3-5) + (7-4)(4-5)}{3-1} = 3 \\ \text{Cov} (X,Y)_{i=1,j=2} &= \frac{(1-4)(5-6) + (4-4)(6-6) + (7-4)(7-6)}{3-1} = 3 \\ \text{Cov} (X,Y)_{i=1,j=3} &= \frac{(1-4)(8-7) + (4-4)(9-7) + (7-4)(10-7)}{3-1} = 3 \end{aligned} Cov(X,Y)i=1,j=1Cov(X,Y)i=1,j=2Cov(X,Y)i=1,j=3=3−1(1−4)(2−5)+(4−4)(3−5)+(7−4)(4−5)=3=3−1(1−4)(5−6)+(4−4)(6−6)+(7−4)(7−6)=3=3−1(1−4)(8−7)+(4−4)(9−7)+(7−4)(10−7)=3
Cov ( X , Y ) i = 2 , j = 1 = ( 2 − 5 ) ( 2 − 5 ) + ( 5 − 5 ) ( 3 − 5 ) + ( 8 − 5 ) ( 4 − 5 ) 3 − 1 = 3 Cov ( X , Y ) i = 2 , j = 2 = ( 2 − 5 ) ( 5 − 6 ) + ( 5 − 5 ) ( 6 − 6 ) + ( 8 − 5 ) ( 7 − 6 ) 3 − 1 = 3 Cov ( X , Y ) i = 2 , j = 3 = ( 2 − 5 ) ( 8 − 7 ) + ( 5 − 5 ) ( 9 − 7 ) + ( 8 − 5 ) ( 10 − 7 ) 3 − 1 = 3 \begin{aligned} \text{Cov} (X,Y)_{i=2,j=1} &= \frac{(2-5)(2-5) + (5-5)(3-5) + (8-5)(4-5)}{3-1} = 3 \\ \text{Cov} (X,Y)_{i=2,j=2} &= \frac{(2-5)(5-6) + (5-5)(6-6) + (8-5)(7-6)}{3-1} = 3 \\ \text{Cov} (X,Y)_{i=2,j=3} &= \frac{(2-5)(8-7) + (5-5)(9-7) + (8-5)(10-7)}{3-1} = 3 \end{aligned} Cov(X,Y)i=2,j=1Cov(X,Y)i=2,j=2Cov(X,Y)i=2,j=3=3−1(2−5)(2−5)+(5−5)(3−5)+(8−5)(4−5)=3=3−1(2−5)(5−6)+(5−5)(6−6)+(8−5)(7−6)=3=3−1(2−5)(8−7)+(5−5)(9−7)+(8−5)(10−7)=3
Cov ( X , Y ) i = 3 , j = 1 = ( 3 − 6 ) ( 2 − 5 ) + ( 6 − 6 ) ( 3 − 5 ) + ( 9 − 6 ) ( 4 − 5 ) 3 − 1 = 3 Cov ( X , Y ) i = 3 , j = 2 = ( 3 − 6 ) ( 5 − 6 ) + ( 6 − 6 ) ( 6 − 6 ) + ( 9 − 6 ) ( 7 − 6 ) 3 − 1 = 3 Cov ( X , Y ) i = 3 , j = 3 = ( 3 − 6 ) ( 8 − 7 ) + ( 6 − 6 ) ( 9 − 7 ) + ( 9 − 6 ) ( 10 − 7 ) 3 − 1 = 3 \begin{aligned} \text{Cov} (X,Y)_{i=3,j=1} &= \frac{(3-6)(2-5) + (6-6)(3-5) + (9-6)(4-5)}{3-1} = 3 \\ \text{Cov} (X,Y)_{i=3,j=2} &= \frac{(3-6)(5-6) + (6-6)(6-6) + (9-6)(7-6)}{3-1} = 3 \\ \text{Cov} (X,Y)_{i=3,j=3} &= \frac{(3-6)(8-7) + (6-6)(9-7) + (9-6)(10-7)}{3-1} = 3 \end{aligned} Cov(X,Y)i=3,j=1Cov(X,Y)i=3,j=2Cov(X,Y)i=3,j=3=3−1(3−6)(2−5)+(6−6)(3−5)+(9−6)(4−5)=3=3−1(3−6)(5−6)+(6−6)(6−6)+(9−6)(7−6)=3=3−1(3−6)(8−7)+(6−6)(9−7)+(9−6)(10−7)=3
故协方差矩阵为
Cov ( X , Y ) = [ 3 3 3 3 3 3 3 3 3 ] \begin{aligned} \text{Cov} (X,Y) &= \left[\begin{matrix} 3 & 3 & 3 \\ 3 & 3 & 3 \\ 3 & 3 & 3 \\ \end{matrix}\right] \end{aligned} Cov(X,Y)= 333333333
Ref
- 如何通俗地解释协方差 - bilibili
- 从3组对应点中求得最佳的旋转和平移变换
相关文章:

【数理知识】协方差,随机变量的的协方差,随机变量分别是单个数字和向量时的协方差
序号内容1【数理知识】自由度 degree of freedom 及自由度的计算方法2【数理知识】刚体 rigid body 及刚体的运动3【数理知识】刚体基本运动,平动,转动4【数理知识】向量数乘,内积,外积,matlab代码实现5【数理知识】协…...

WebDAV之π-Disk派盘+可达漫画
可达漫画这是一款专为阅读你的漫画收藏而设计的阅读器。 热爱漫画的你肯定收藏了不少各种类型的漫画,它们可能有各种各样的格式,zip,rar,cbz,cbr,epub, mobi 或 pdf,也可能只是单纯的文件夹。 可达漫画支持「流式阅读」,如果你的服务器使用 WebDAV 或 SMB 协议,那么…...

Spring中Bean的线程安全问题
Spring框架本身没有明确指出Bean的线程安全问题,所以Bean本身也不具备线程安全的特性,具体情况得看scope的情况。 1.原型的(prototype) 每次创建一个新的对象,每个线程使用的对象都是要新创建的,所以不会存在线程安全的问题。 2…...
Java spring boot 全解Camunda 7,从 0 到 1 构建工作流平台——第二节:Spring boot 简单集成
目录 1. 成果展示2. 环境准备3. 项目构建3.1 项目结构3.2 引入Camunda 依赖3.3 启动spring boot 程序3.4 启动 web app 程序 引言:当今技术发展迅猛,企业对于业务流程的高效管理和自动化需求也日益增长。在这个背景下,Spring Boot和Camunda7成…...

手持式静电测试仪的运用原理
手持式静电测试仪(Handheld Electrostatic Test Meter)是一种用于测量和检测静电电荷的便携式设备。它通常用于工业生产、实验室研究、防静电控制和监测等领域。 手持式静电测试仪可以帮助用户快速准确地测量物体表面静电电荷的状态,从而评估…...

【css问题】flex布局中,子标签宽度超出父标签宽度,导致布局出现问题
场景:文章标题过长时,只显示一行,且多余的部分用省略号显示。 最终效果图: 实现时,flex布局,出现问题: 发现text-overflow: ellipsis不生效,省略符根本没有出现。 而且因为设置了 …...

【vue3】前端应用中使用WebSocket与服务器进行通信并管理连接状态。
1、写一个hook函数 export const useWebsocketToStore ({ onMessage }): any > {const url ws:地址 Math.random()const onConnected () > {}const onDisconnected () > {}const onError () > {}const onMessageDefault (ws: WebSocket, event: MessageEve…...
服务端高并发分布式结构演进之路
目录 一、常见概念 1.1基本概念 二、架构演进 2.1单机架构 2.2应用数据分离架构 2.3应用服务集群架构 2.4读写分离 / 主从分离架构 2.5引入缓存 —— 冷热分离架构 2.6垂直分库 2.7业务拆分 —— 微服务 一、常见概念 1.1基本概念 应用(Application&am…...

微服务基础总结
1.服务注册和发现 服务注册维护一个登记簿,管理系统内所有服务地址,服务启动后会向登记簿交待自己的地址信息。 服务注册形式:客户端注册和第三方注册 客户端注册(zookeeper) 服务自身要负责注册和注销工作…...
实现vscode上用gdb调试stm32
实现vscode上用gdb调试stm32 这周负责编写设备的某个模块,其中遇到了一些变量地址不正确的错误,按理这种底层变量错误用gdb一类的调试器就能很快查到,可是初入嵌入式一行,此C语言非彼C语言,对于gdb怎么对接到项目上根…...
第4章 变量、作用域与内存
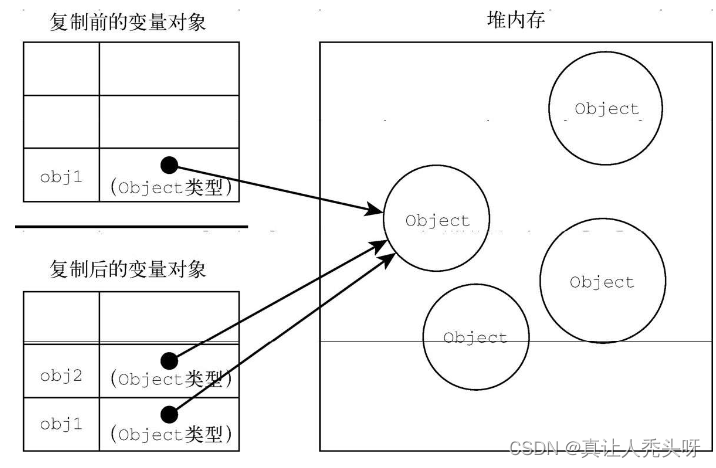
引言 由于js是一门只有在声明变量后才能明确类型的语言,并且在任意时刻都可以改变数据类型。这也引起了一些问题 原始值与引用值 原始值就是基本数据类型,引言值就是复杂数据类型 变量在赋值的时候。js会判断如果是原始值,访问时就是按值访问…...

Python爬虫遇到重定向问题解决办法汇总
在进行Python爬虫任务时,遇到重定向问题是常见的问题之一。重定向是指在发送请求时,服务器会返回一个新的URL,将请求重新定向到该URL。为了帮助您解决这个问题,本文将提供一些实用的解决办法,并给出相关的代码示例&…...

R并行计算
1-lapply()函数介绍: 为什么介绍这个函数呢?因为在windows中使用parLapply()函数和lapply()的结构和用法是非常相似的,我们只需要将原本用lapply(x, fun)迭代函数 直接改写成 parLapply(makeCluster(c1), x, fun)即可,这里的直接…...

STM32 低功耗-待机模式
STM32 待机模式 文章目录 STM32 待机模式第1章 低功耗模式简介第2章 待机模式简介2.1 进入待机模式2.1 退出待机模式 第3章 待机模式代码部分总结 第1章 低功耗模式简介 在 STM32 的正常工作中,具有四种工作模式:运行、睡眠、停止和待机模式。 在系统或…...
极海APM32F003F6P6烧写问题解决记录
工作中遇到的,折腾了好久,因为电脑重装过一遍系统,软件也都重新安装了,所以不知道之前的配置是什么,旧项目代码编译没问题,烧写时疯狂报错,用的是JLink。 keil版本v5.14 win10版本 JLink版本…...

【大数据】Flink 详解(一):基础篇
Flink 详解(一):基础篇 1、什么是 Flink ? Flink 是一个以 流 为核心的高可用、高性能的分布式计算引擎。具备 流批一体,高吞吐、低延迟,容错能力,大规模复杂计算等特点,在数据流上提…...

ChatGPT 作为 Python 编程助手
推荐:使用 NSDT场景编辑器 助你快速搭建可编辑的3D应用场景 简单的数据处理脚本 我认为一个好的起点是某种数据处理脚本。由于我打算让 ChatGPT 之后使用各种 Python 库编写一些机器学习脚本,这似乎是一个合理的起点。 目标 首先,我想尝试…...

饿了么输入框限制只能输入数字,并且保留小数
可以使用饿了么ui中的input-number组件实现输入框只能输入数字,这样就不能输入数字以外的,controls隐藏输入框左右俩边的加减按钮,precision小数点保留多少位,2则是俩位,但是会导致默认值为0.00的情况,俩种…...

kylin-Desktop gsettings 获取或设置系统配置
gsettings提供了对GSetings的命令行操作。GSetings实际上是一套高级API,用来操作dconf。 dconf存储着GNOME3的配置,是二进制格式。它做为GSettings的后端系统存在,暴露出低级API。在GNOME2时代,类似的角色是gconf,但它是以XML文本形式存储。 更接地气的说法是,dconf是G…...

setmap使用
目录 set使用 set的模板参数 构造函数 成员函数 insert iterator 编辑 find count pair pair 的模板参数 make_pair multiset使用 multiset 的模板参数 set 与 multiset 的区别 count map使用 map 的模板参数 构造函数 insert iterator find 编辑 cou…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

webpack面试题
面试题:webpack介绍和简单使用 一、webpack(模块化打包工具)1. webpack是把项目当作一个整体,通过给定的一个主文件,webpack将从这个主文件开始找到你项目当中的所有依赖文件,使用loaders来处理它们&#x…...
 ----- Python的类与对象)
Python学习(8) ----- Python的类与对象
Python 中的类(Class)与对象(Object)是面向对象编程(OOP)的核心。我们可以通过“类是模板,对象是实例”来理解它们的关系。 🧱 一句话理解: 类就像“图纸”,对…...

Win系统权限提升篇UAC绕过DLL劫持未引号路径可控服务全检项目
应用场景: 1、常规某个机器被钓鱼后门攻击后,我们需要做更高权限操作或权限维持等。 2、内网域中某个机器被钓鱼后门攻击后,我们需要对后续内网域做安全测试。 #Win10&11-BypassUAC自动提权-MSF&UACME 为了远程执行目标的exe或者b…...
