线段树思想拆解(下篇)
线段树思想拆解(下篇)
上篇回顾
到这里我们已经处理好了初始化以及添加方法,接下来实现范围的 query 方法
public int query(int queryL, int queryR) {return query(queryL, queryR, 1, orgLength - 1, 1);}
到此为止通过借助 sum 数组,lazy 数组就已经实现了在范围内统一增加一个数值,查询范围总和的时间复杂度为 O(logN) 了,接下来要引入更新操作,对于更新操作我们需要再借助两个数组来维护更新的懒操作。
接上篇来讲,注意一下我们所有方法的 L 和 R 的范围都是指源数组的范围,即源数组是 8 个数字,则范围为 1-8 , 而对于我们的逻辑线段树数组是通过 index 进行计算得到表示范围的节点数组槽位。
增加 Update 方法
对于 update 方法,思路和 add 方法基本一样,但是如果要同时支持两个方法,需要考虑 update 方法会覆盖之前的 lazyAdd 的缓存任务。
首先提供一个递归调用的 update 方法,然后开放一个简化调用的 update 方法,如下:
private void update(int updateL, int updateR, int operateL, int operateR, int treeIndex, int updateNum) {// 全包直接可以更新if (updateL <= operateL && operateR <= updateR) {lazyUpdate[treeIndex] = updateNum;lazyUpdateFlag[treeIndex] = true;// 直接更新 sumsum[treeIndex] = updateNum * (operateR - operateL + 1);// 清空覆盖懒增加lazyAdd[treeIndex] = 0;return;}// 如果包不住,需要进行下发处理int mid = (operateL + operateR) >> 1;// 懒任务下发pushDownLazyTask(treeIndex, mid - operateL + 1, operateR - mid);if (updateL <= mid) {update(updateL, updateR, operateL, mid, treeIndex << 1, updateNum);}if (updateR > mid) {update(updateL, updateR, mid + 1, operateR, treeIndex << 1 | 1, updateNum);}sum[treeIndex] = sum[treeIndex << 1] + sum[treeIndex << 1 | 1];
}
这里提一下,我在第一次实现的时候,理所应当的思考就和 lazyAdd 一样,提供一个 lazyUpdate[] 数组来阻塞更新的下发就可以了,但是实际实现后是无法通过对数器的,因为无法判断是否有更新,我们无法简单的判断 lazyUpdate[index] != 0 就认定没有更新,有可能就是更新到了 0,所以需要一个标记更新的数组,最后我定义了 lazyUpdateFlag 来辅助判断是否有更新。
所以新增的结构为
private int[] lazyUpdate;
// 单独用一个数组标记是否进行了更新
private boolean[] lazyUpdateFlag;
对于懒任务下发就需要增加处理更新任务下发的逻辑
private void pushDownLazyTask(int index, int leftRange, int rightRange) {// 根据更新标记数组判断是否有懒更新,不然更新 0 的时候没法判断if (lazyUpdateFlag[index]) {int lazyUpdateNum = lazyUpdate[index];lazyUpdate[index] = 0;lazyUpdateFlag[index] = false;int left = index << 1;int right = index << 1 | 1;lazyAdd[left] = 0;lazyAdd[right] = 0;lazyUpdate[left] = lazyUpdateNum;lazyUpdateFlag[left] = true;lazyUpdate[right] = lazyUpdateNum;lazyUpdateFlag[right] = true;sum[left] = leftRange * lazyUpdateNum;sum[right] = rightRange * lazyUpdateNum;}// 这里最后还是会执行一遍懒添加的下发,因为存在先懒更新后再懒添加的情况,这块更新会清空覆盖懒添加,所以不会有先添加后更新的问题if (lazyAdd[index] != 0) {int lazyNum = lazyAdd[index];lazyAdd[index] = 0;lazyAdd[index << 1] += lazyNum;lazyAdd[index << 1 | 1] += lazyNum;sum[index << 1] += leftRange * lazyNum;sum[index << 1 | 1] += rightRange * lazyNum;}
}
这里对于懒更新,因为进行了下发,所以清除更新、添加,计算 sum 数组
最后对数器验证通过
public static void main(String[] args) {//对数器int testTimes = 5000;int addOrUpdateTimes = 5000;int maxAddOrUpdateNum = 5000;int testQueryTimes = 5000;Random random = new Random();//进行测试for (int i = 0; i < testTimes; i++) {int[] origin = RandomUtil.generateArray(30, 10);// System.out.println(Arrays.toString(origin));SegmentTree segmentTree = new SegmentTree(origin);SegmentTreeON segmentTreeON = new SegmentTreeON(origin);int originLength = origin.length;//每次测试进行添加更新操作次数for (int j = 0; j < addOrUpdateTimes; j++) {int num1 = random.nextInt(originLength) + 1;int num2 = random.nextInt(originLength) + 1;int L = Math.min(num1, num2);int R = Math.max(num1, num2);int num = random.nextInt(maxAddOrUpdateNum);if (random.nextInt(10) < 5) {segmentTree.add(L, R, num);segmentTreeON.add(L, R, num);} else {segmentTree.update(L, R, num);segmentTreeON.update(L, R, num);}}for (int k = 0; k < testQueryTimes; k++) {int num1 = random.nextInt(originLength) + 1;int num2 = random.nextInt(originLength) + 1;int L = Math.min(num1, num2);int R = Math.max(num1, num2);if (segmentTree.query(L, R) != segmentTreeON.query(L, R)) {System.out.println("L-R=" + L + "-" + R);System.out.println("segmentTree.query(L,R)=" + segmentTree.query(L, R));System.out.println("segmentTreeON.query(L,R)=" + segmentTreeON.query(L, R));System.out.println("error!!!!! testNum=" + k);return;}}System.out.println("right " + (i + 1));}
}
相关文章:
)
线段树思想拆解(下篇)
线段树思想拆解(下篇) 上篇回顾 到这里我们已经处理好了初始化以及添加方法,接下来实现范围的 query 方法 public int query(int queryL, int queryR) {return query(queryL, queryR, 1, orgLength - 1, 1);}到此为止通过借助 sum 数组&…...
Containerd容器镜像管理
1. 轻量级容器管理工具 Containerd 2. Containerd的两种安装方式 3. Containerd容器镜像管理 4. Containerd数据持久化和网络管理 1、Containerd镜像管理 1.1 Containerd容器镜像管理命令 docker使用docker images命令管理镜像单机containerd使用ctr images命令管理镜像,con…...
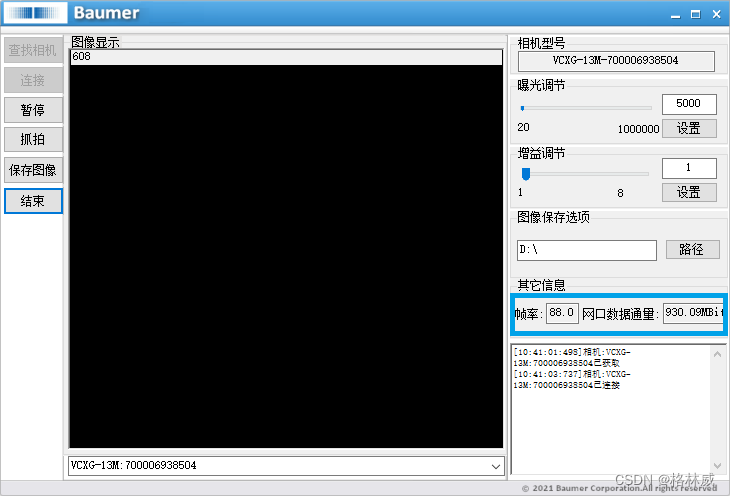
Baumer工业相机堡盟工业相机如何通过BGAPI SDK获取相机当前数据吞吐量(C#)
Baumer工业相机堡盟工业相机如何通过BGAPISDK里函数来获取相机当前数据吞吐量(C#) Baumer工业相机Baumer工业相机的数据吞吐量的技术背景CameraExplorer如何查看相机吞吐量信息在BGAPI SDK里通过函数获取相机接口吞吐量 Baumer工业相机通过BGAPI SDK获取…...

Ubuntu服务器版配置wifi
最近把曾经不用的上网本安装了一个Ubuntu-Server版,当成服务器来用,因为家庭网络布线问题,只好用自带的WIFI来连接网络,Server版也没有什么图形化的管理工具,之后手动编辑配置文件了。 Server下面配置起来还是很方便的…...

Windows 主机的VMware 虚拟机访问 wsl-ubuntu 的 API 服务
Windows 主机的VMware 虚拟机访问 wsl-ubuntu 的 API 服务 0. 背景1. 设置2. 删除 0. 背景 需要从Windows 主机的VMware 虚拟机访问 wsl-ubuntu 的 API 服务。 1. 设置 Windows 主机的IP:192.168.31.20 wsl-ubuntu Ubuntu-22.04 的IP:172.29.211.52 &…...
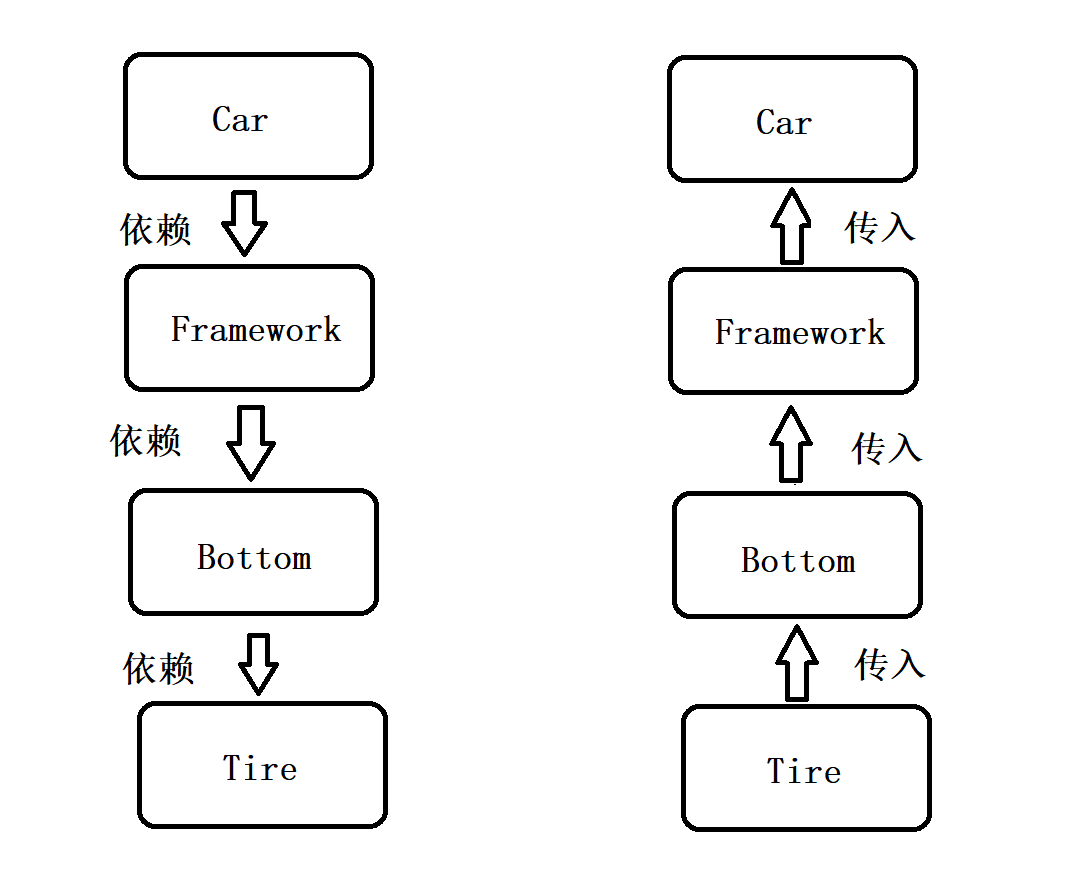
【Spring】(一)Spring设计核心思想
文章目录 一、初识 Spring1.1 什么是 Spring1.2 什么是 容器1.3 什么是 IoC 二、对 IoC 的深入理解2.1 传统程序开发方式存在的问题2.2 控制反转式程序的开发2.3 对比总结 三、对 Spring IoC 的理解四、DI 的概念4.1 什么是 DI4.2 DI 与 IoC的关系 一、初识 Spring 1.1 什么是…...

chrome插件开发实例04-智能收藏夹
目录 功能说明 演示 源码下载 源代码 manifest.json popup.html popup.js background.js 功能说明 基于chrome插件...

iOS技术之 手机系统15.0之后 的 UITableView section header多22像素问题
iOS 15 的 UITableView又新增了一个新属性:sectionHeaderTopPadding 会给每一个section header 增加一个默认高度,当我们 使用 UITableViewStylePlain 初始化 UITableView的时候,就会发现,系统给section header增高了22像素。 解…...
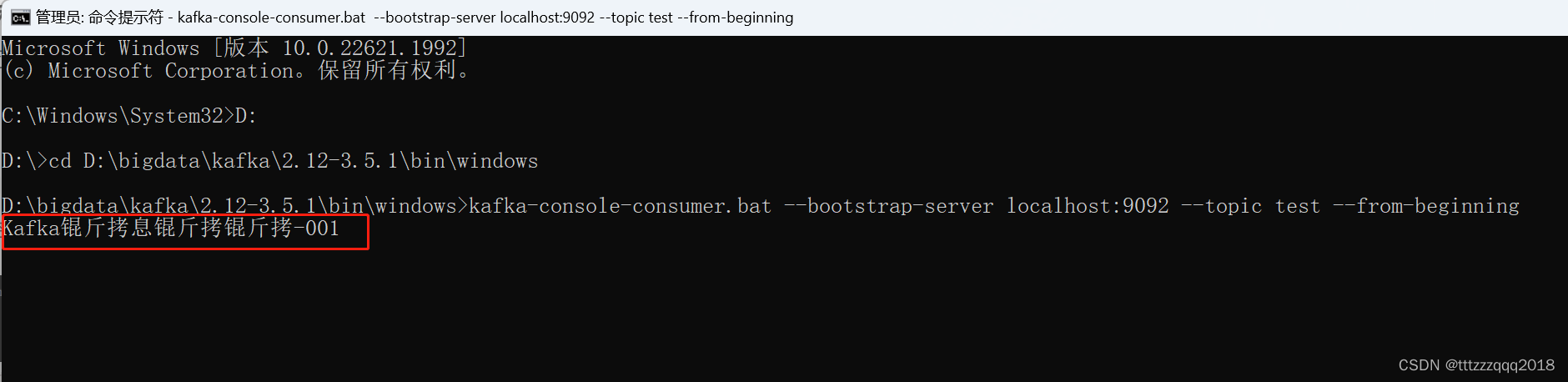
Windows下安装Kafka(图文记录详细步骤)
Windows下安装Kafka Kafka简介一、Kafka安装前提安装Kafka之前,需要安装JDK、Zookeeper、Scala。1.1、JDK安装(version:1.8)1.1.1、JDK官网下载1.1.2、JDK网盘下载1.1.3、JDK安装 1.2、Zookeeper安装1.2.1、Zookeeper官网下载1.2.…...

linuxARM裸机学习笔记(3)----主频和时钟配置实验
引言:本文主要学习当前linux该如何去配置时钟频率,这也是重中之重。 系统时钟来源: 32.768KHz 晶振是 I.MX6U 的 RTC 时钟源, 24MHz 晶振是 I.MX6U 内核 和其它外设的时钟源 1. 7路PLL时钟源【都是从24MHZ的晶振PLL而来…...

防勒索病毒
随着勒索软件攻击在2023年的激增,网络安全已成为当今最重要的议题之一。根据区块链分析公司Chainaanalysis的最新报告,勒索软件攻击已成为唯一呈增长趋势的基于加密货币的犯罪行为,勒索金额更是比一年前增加了近1.758亿美元,达到4…...

剑指 Offer 53 - II. 0~n-1 中缺失的数字
力扣 一个长度为n-1的递增排序数组中的所有数字都是唯一的,并且每个数字都在范围0~n-1之内。在范围0~n-1内的n个数字中有且只有一个数字不在该数组中,请找出这个数字。 示例 1: 输入: [0,1,3] 输出: 2 示例 2: 输入: [0,1,2,3,4,5…...

vue2和vue3区别
vue2和vue3的区别有以下8点: 1、双向数据绑定原理不同; 2、是否支持碎片; 3、API类型不同; 4、定义数据变量和方法不同; 5、生命周期钩子函数不同; 6、父子传参不同; 7、指令与插槽不同&#x…...

IMV3.0
经历了两个版本,基础内容在前面,可以使用之前的基础环境: v1: https://blog.csdn.net/wtt234/article/details/132139454 v2: https://blog.csdn.net/wtt234/article/details/132144907 一、代码组织结构 二、代码 2.…...
怎么在树莓派环境上搭建web网站,并发布到外网可访问,今天教给大家
怎么在树莓派上搭建web网站,并发布到外网可访问? 文章目录 怎么在树莓派上搭建web网站,并发布到外网可访问?概述使用 Raspberry Pi Imager 安装 Raspberry Pi OS测试 web 站点安装静态样例站点 将web站点发布到公网安装 Cpolarcpo…...

大文件传输软件| 生命科学中的关键因素
在2023年,生命科学领域以及其先进的科学技术吸引了人们的目光。这些研究背后,很少有人知道的是,其中涉及了大量的研究数据需要实时进行文件传输,以便于研究,合作,分享,分析,临床试验…...

varint编码实现原理
简言 1. varint即 variable int,也就是变长整型,在mysql,levelDB,protobuf中都有使用 2. varint编码的优点是对数值较小的数进行编码后占用字节较少,比如[0-127]只占用1个字节,[128~16383]只占用2个字节。…...

如果新电脑是刚安装的mysql,但是旧电脑迁移过来的文件里面有相关的rails文件,运行rake db:migrate一直报错
$ bundle exec rake db:migrate#运行完命令报错 rake aborted! LoadError: libmysqlclient.so.21: cannot open shared object file: No such file or directory - /home/meiyi/.asdf/installs/ruby/2.6.9/lib/ruby/gems/2.6.0/gems/mysql2-0.5.5/lib/mysql2/mysql2.so /home/m…...

ChatGPT已闯入学术界,Elsevier推出AI工具
2022年11月,OpenAI公司发布了ChatGPT,这是迄今为止人工智能在现实世界中最重要的应用之一。 当前,互联网搜索引擎中出现了越来越多的人工智能(AI)聊天机器人,例如谷歌的Bard和微软的Bing,看起来…...
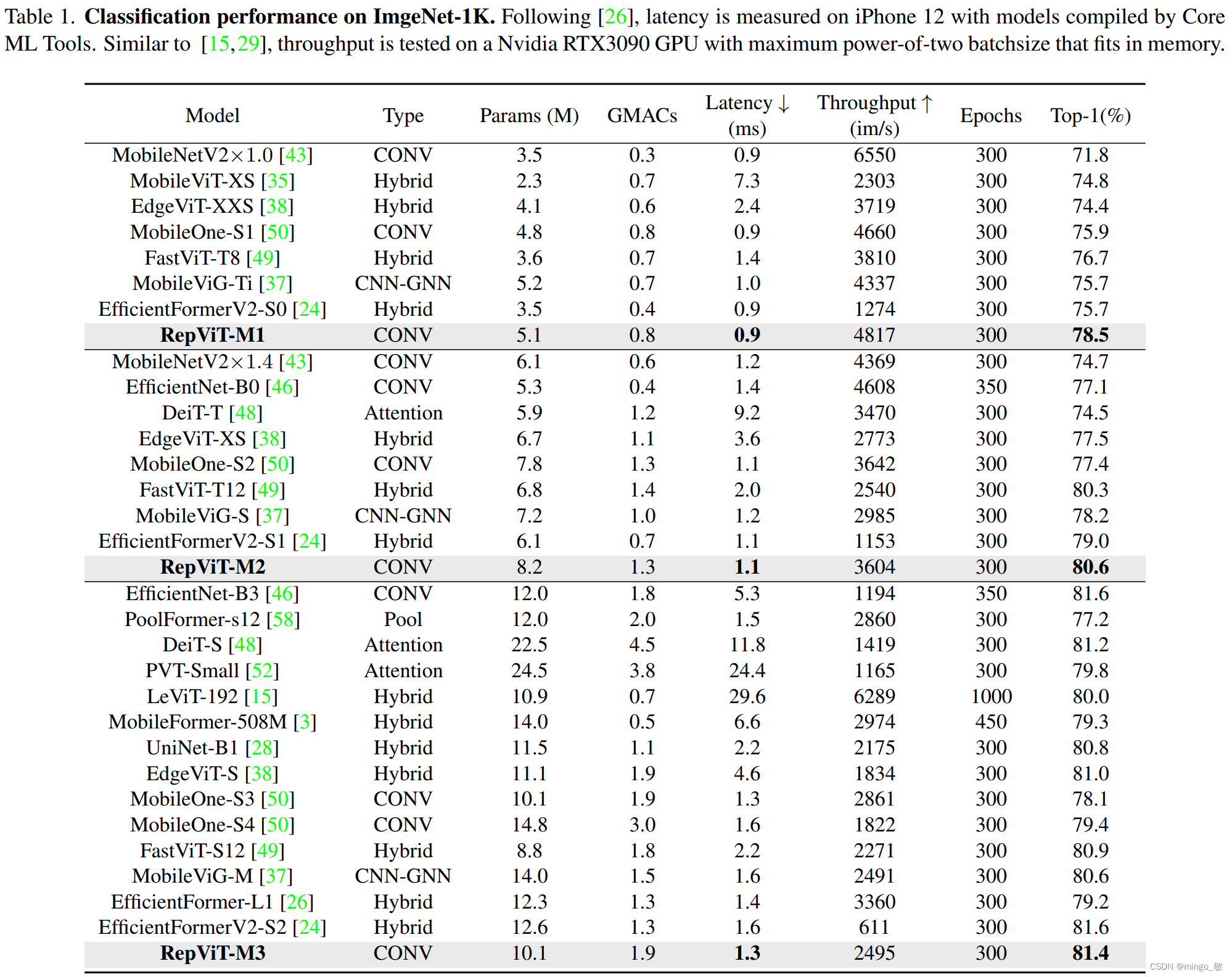
深度学习论文: RepViT: Revisiting Mobile CNN From ViT Perspective及其PyTorch实现
深度学习论文: RepViT: Revisiting Mobile CNN From ViT Perspective及其PyTorch实现 RepViT: Revisiting Mobile CNN From ViT Perspective PDF: https://arxiv.org/pdf/2307.09283.pdf PyTorch代码: https://github.com/shanglianlm0525/CvPytorch PyTorch代码: https://gith…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...
