【排序算法略解】(十种排序的稳定性,时间复杂度以及实现思想)(含代码)(完工于2023.8.3)
文章目录
- 1、冒泡排序/选择排序/插入排序
- 冒泡排序(Bubble Sort)
- 选择排序(Selection Sort)
- 插入排序(Insertion Sort)
- 2、希尔排序(Shell's Sort)
- 3、快速排序(Quick Sort)
- 4、堆排序(Heap Sort)
- 5、归并排序(Merge Sort)
- 6、桶排序/计数排序/基数排序
- 桶排序(Bucket sort)
- 计数排序(Counting Sort)
- 基数排序(Radix Sort)
注:以下排序默认为升序排序。
稳定性:指的是排序的过程中是否会改变多个相同的值的相对次序,如果会改变则是不稳定的。
1、冒泡排序/选择排序/插入排序
冒泡排序,选择排序,插入排序是最简单的排序方法。
冒泡排序(Bubble Sort)
排序方法:扫描的过程中,比较相邻两个数的大小关系,如果存在逆序就交换这两个数,这样每趟可以保证最后一个数,也就是最大的数,一步步交换上去,如气泡上浮一样,回归到正确的位置。
时间复杂度: O ( n 2 ) O(n^2) O(n2)
稳定性:稳定。对于两个相同的值,不会发生交换。
代码实现:
int arr[] = {0, 2, 9, 3, 5, 7, 8, 1, 4, 6};//arr是被排序数组,start是起点坐标,end是终点坐标(闭区间)void sort(int* arr, int start, int end) {int n = end - start + 1;//只需要排序n - 1次for (int i = 1; i < n; i++) {//倒数i - 1个数已经归位不必交换for (int j = start; j <= end - i; j++) {//出现逆序if (arr[j + 1] < arr[j]) {int tmp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = tmp;}}}
}
选择排序(Selection Sort)
排序方法:扫描的过程中,每次选择剩余未排序的数组中选择最小值与未排序部分第一个值进行交换,从而使得未排序部分的第一个位置得到正确的值。
时间复杂度: O ( n 2 ) O(n^2) O(n2)
稳定性:不稳定。例如,3 3 2 → 一次交换 \stackrel{一次交换}{\rightarrow} →一次交换 2 3 3 可以发现两个3的位置改变了。
代码实现:
int arr[] = {0, 2, 9, 3, 5, 7, 8, 1, 4, 6};//arr是被排序数组,start是起点坐标,end是终点坐标(闭区间)void sort(int* arr, int start, int end) {int n = end - start + 1;//只需要排序n - 1次for (int i = 1; i < n; i++) {int min_element_positon = start + i - 1;for (int j = start + i - 1; j <= end; j++) {if (arr[j] < arr[min_element_positon]) {min_element_positon = j;}}int tmp = arr[min_element_positon];arr[min_element_positon] = arr[start + i - 1];arr[start + i - 1] = tmp;}
}
插入排序(Insertion Sort)
排序方法:每次取未排序部分的数组,将其插入到前半已经排序后的数组内,类似打牌时整理牌序的方法,插入到前面整理好的数组内的合适的位置。
时间复杂度: O ( n 2 ) O(n^2) O(n2)
稳定性:稳定。相同的值符合大于等于关系,并不会插入到相同值的前面。
代码实现:
int arr[] = {0, 2, 9, 3, 5, 7, 8, 1, 4, 6};//arr是被排序数组,start是起点坐标,end是终点坐标(闭区间)void sort(int* arr, int start, int end) {int n = end - start + 1;//只需要排序n - 1次for (int i = 1; i < n; i++) {int key = arr[start + i];int j = start + i;while (j >= start) {if (j == start) break; // 如果是最小值,会一直到开头if (j == start + i && key >= arr[j - 1]) break; //如果是最大值if (key >= arr[j - 1] && key <= arr[j + 1]) break;//在中间合适的值arr[j] = arr[j - 1];j--;}arr[j] = key;}
}
2、希尔排序(Shell’s Sort)
排序方法:每次选择特定的增量,对这个增量下的子序列进行直接插入排序。
最好时间复杂度: O ( n log n ) O(n\log{n}) O(nlogn)
最坏时间复杂度: O ( n n ) O(n\sqrt{n}) O(nn)【选取d={1, 2, 4, 8, …2k}大到小】,$O(n\log{n}\log{n})$【选取2m*2^n次大到小的集合】
关于时间复杂度的证明:主要考虑对于两个不同增量的序列的插入排序,两者的结果都是可以互相继承的;以及相关其他复杂度的 分析
稳定性:不稳定,因为不同序列相同的值的位置可能改变。
代码实现:
int arr[] = {0, 2, 9, 55, 54, 7, 8, 1, 40, 600};void sort(int* arr, int start, int end) {int n = end - start + 1;for (int d = n / 2; d >= 1; d /= 2) {//倍减for (int i = d; i < n; i++) {//一共进行n - d次插入int tmp = arr[start + i];//取无序部分第一个数进行插排int j = i - d;for (; j >= 0 && tmp < arr[j + start]; j -= d) {arr[j + d + start] = arr[j + start];}//如果前面有比最后一个数小的,就腾出一位//实际上会多减一次,要补回darr[j + d + start] = tmp;}}
}
3、快速排序(Quick Sort)
排序方法:“挖坑填数”,取出需要排序区间的第一个数作为基数,利用双指针方法,整理当前数组,使得这个数组成为坑左边均为小于等于基数的数,坑右边都是大于等于基数的数,最后把基数填入这个位置,此处基数回到正确的位置。然后分成两个区间,递归分治,重复上述操作。
一般时间复杂度: O ( n log ( n ) ) O(n\log(n)) O(nlog(n))
最坏时间复杂度(例如数组已经有序的时候): O ( n 2 ) O(n^2) O(n2)
稳定性:不稳定。例如 6 3 3 经过一次的填坑得到 3 3 _ 3的次序发生了改变。
代码实现:
int arr[] = {0, 2, 9, 3, 5, 7, 8, 1, 4, 6};//arr是被排序数组,start是起点坐标,end是终点坐标(闭区间)void sort(int* arr, int start, int end) {if (start >= end) { //如果只有1个元素,或者没有元素就不需要排序return;}//目的是把数组整理成一半小于等于基数,一半大于等于基数,中间是坑位的样子int l = start, r = end, key = arr[l];//取第一个元素作为基数while (l < r) {while (l < r && arr[r] >= key) {r--;//从后往前找到第一个小于key的值}if (l < r) {//如果相遇则说坑位左右两侧都已经整理完毕arr[l++] = arr[r];}while (l < r && arr[l] <= key) {l++;//从前往后找到第一个大于key的值}if (l < r) {arr[r--] = arr[l];}}arr[l] = key;sort(arr, start, l - 1);sort(arr, l + 1, end);
}
4、堆排序(Heap Sort)
排序方法:利用标号关系构造一个无序堆,通过堆调整,形成一个有序的大顶堆。每次取堆顶的数和未排序数的最大标号,即堆底最后一个叶子交换位置,此时,最后一个叶子是当前未排序的数中最大的数,已经回到正确的位置,离开堆。之后,调整堆,维护大顶堆的性质,等待下一次交换。
关于堆调整:如果父节点最大不交换,如果父节点不是最大,则要交换左右儿子中较大的一个,交换后,可以使得原来那个较小儿子所在的子树的父节点变成较大儿子,这样保证较小儿子的子树符合二叉堆的性质,并且根节点也符合条件,但是,可能会影响较另外子数成堆,所以,为了维护堆的性质,要一直交换下去,直到符合性质,最坏可能要交换到叶子,但是这样的交换不超过 log n \log{n} logn次,因为每次交换都可以使得近似大小的另一子树符合堆的性质,需要维护的堆的性质的节点数倍减,直至单个节点,单个节点符合堆的性质。
时间复杂度: O ( n log n ) O(n\log{n}) O(nlogn)
时间复杂度分析:开始的堆调整 n n n次,之后每个数取出后的堆调整的交换次数取决于二叉堆的深度,由于二叉堆是一个完全二叉树,所以深度不超过 log n \log{n} logn所以一趟的交换次数不超过 log n \log{n} logn次。
稳定性:不稳定。如果是全相等的堆,仍然会进行交换。
代码实现:
int arr[] = {0, 2, 9, 3, 5, 7, 8, 1, 4, 6};//arr是被排序数组,start是起点坐标,end是终点坐标(闭区间)
//堆调整函数,维护当前子树堆的性质
void heap_modify(int* arr, int root_id, int last_id, int start) {int tmp = arr[root_id + start];for (int i = 2 * root_id + 1; i <= last_id; i = i * 2 + 1) {//枚举左儿子if (i < last_id && arr[i + start] < arr[i + 1 + start]) {//如果有右儿子,并且右儿子更大,取右儿子进行比较//否则取左儿子i++;}//较大的儿子和根节点进行比较,都是和原来根节点交换的数进行比较if (arr[i + start] > tmp) {arr[root_id + start] = arr[i + start];root_id = i;//较大的儿子的id是根节点的下一个id}else {//如果较大的儿子不大于根节点,不必调整下去break;}}arr[root_id + start] = tmp;//填坑
}
void sort(int* arr, int start, int end) {//构造有序堆for (int i = end; i >= start; i--) {//映射成0~n的标号,倒着整理heap_modify(arr, i - start, end - start, start);}int n = end - start + 1;for (int i = 1; i < n; i++) {//n - 1趟int tmp = arr[start];arr[start] = arr[end - i + 1];//与当前无序数组最大下标交换arr[end - i + 1] = tmp;heap_modify(arr, 0, end - i - start, start);//维护堆的性质}
}
5、归并排序(Merge Sort)
排序方法:利用分治的思想,将数组不断划分,到单个数,然后递归合并起来,利用双指针的手法,将两个有序数组合并成一个有序的数组。
时间复杂度: O ( n log n ) O(n\log{n}) O(nlogn)
稳定性:稳定,合并的数组的时候,如果两个值相同的话会按照原先的顺序依次放入到临时数组当中。
代码实现:
int arr[] = {0, 2, 9, 55, 54, 7, 8, 1, 40, 600};
int tmp[1000];
void merge_arr(int* arr, int* tmp, int start, int end, int mid) {int i = start, j = mid + 1, p = 0;//要保证归并排序的稳定性,<=的时候优先取左侧while (i <= mid && j <= end) {if (arr[i] <= arr[j]) {tmp[p++] = arr[i++];} else {tmp[p++] = arr[j++];}}//当一个数组填完了,剩余的部分要填完,也就是另一个数组内不存在小于等于这个数的数据了while (i <= mid) {tmp[p++] = arr[i++];}while (j <= end) {tmp[p++] = arr[j++];}//回填入数组for (int k = start; k <= end; k++) {arr[k] = tmp[k - start];}
}
void sort(int* arr, int start, int end) {//二分区间if (start < end) {//这个条件需要否则会无限递归int mid = (start + end) >> 1;sort(arr, start, mid);//分成start~mid mid+1~end两个区间sort(arr, mid + 1, end);merge_arr(arr, tmp, start, end, mid);}
}
6、桶排序/计数排序/基数排序
桶排序(Bucket sort)
排序方法:将输入值的值域划分成若干个区间,分别放入到桶中,再用其他排序方法对桶内的元素进行排序,类似分块,分治。
时间复杂度:取决于桶内排序算法的时间复杂度以及分类后所在的桶的数目,如果使用堆排序来进行桶内排序的话,并且最后均匀地分入到k个桶内,那么时间复杂度是 O ( n + n log n k ) O(n+n\log{\frac{n}{k}}) O(n+nlogkn),当桶足够多时,覆盖了值域的时候,便是 O ( n ) O(n) O(n)的计数排序。
稳定性:取决于给桶内排序的算法的稳定性,如果是插入排序就是稳定的,如果是堆排序或者快速排序就是不稳定的。
代码实现:
int arr[] = {0, 2, 9, 3, 5, 7, 8, 1, 4, 6};//arr是被排序数组,start是起点坐标,end是终点坐标(闭区间)void sort(int* arr, int start, int end, int bucket_size) {int min_value = arr[start];int max_value = arr[start];//获得值域for (int i = start; i <= end; i++) {if (arr[i] < min_value) {min_value = arr[i];}if (arr[i] > max_value) {max_value = arr[i];}}int val_area = max_value - min_value + 1;int bucket_nums = (val_area + bucket_size - 1) / bucket_size;//获得向上取整的桶的数目//如果此处size为4,分成 0~3, 4~7, 8~9三个桶,标号分别是0 1 2for (int i = start; i <= end; i++) {int x = arr[i];int id = (x - min_value) / bucket_size;buckets[id][elements_in_bukect[id]++] = x;//填入一个数字}for (int i = 0; i < bucket_nums; i++) {if (elements_in_bukect[i] == 0) continue;int len = elements_in_bukect[i];heap_sort(buckets[i], 0, len - 1);}//回收排序好的数字int p = 0;for (int i = 0; i < bucket_nums; i++) {if (elements_in_bukect[i] == 0) continue;int len = elements_in_bukect[i];for (int j = 0; j < len; j++) {arr[p + start] = buckets[i][j];p++;}}
}
计数排序(Counting Sort)
排序方法:计数排序是桶排序中桶的数量和值域长度相同的时候,就是一次读入数据,放入到对应值的桶内,最后遍历值域输出排序好的数组。
时间复杂度: O ( n + k ) O(n+k) O(n+k)其中k是值域长度,n是元素数目。
稳定性:稳定。按序读入相同值,按序拷贝出来。笔者想了想,直接用一维数组有点难以体现稳定性,如果用可变长数组或者链表来实现的话就能维护相同值的相对次序,每个链表存入该值的id。或者用二维数组。
代码实现:
int arr[] = {0, 2, 9, 3, 5, 7, 8, 1, 4, 6};//这里没有用链表
int cnt[100];
void sort(int* arr, int start, int end) {int min_value = arr[start];int max_value = arr[start];for (int i = start; i <= end; i++) {if (arr[i] < min_value) {min_value = arr[i];}if (arr[i] > max_value) {max_value = arr[i];}}for (int i = start; i <= end; i++) {cnt[arr[i] - min_value]++;}int p = start;for (int i = 0; i <= max_value - min_value; i++) {for (int j = 0; j < cnt[i]; j++) {arr[p++] = i + min_value;}}
}
基数排序(Radix Sort)
排序方法:基数排序相当于对每一位作计数排序。
时间复杂度: O ( k ⋅ n ) O(k·n) O(k⋅n)其中k是最大数的某进制形式下的数码长度(通常是十进制)
原理说明:手写高位到低位分别是主要关键字,次要关键字,,,次次关键字,最次关键字。首先我们根据最低位排序,如果后面高位不相同,会按照高位排序,如果高位相同的话,但是低位不相同,计数排序具有稳定性,不会改变低位已经排好的顺序。
稳定性:稳定。同上。
注意:基数排序的需要非负整数,如果有负数的话需要调整为非负整数。
代码实现:
int arr[] = {0, 2, 9, 3, 5, 7, 8, 1, 40, 600};//这里没有用链表
int buckets[10][10000];//数码桶,一个桶里可以装10000个数
int elements_in_bucket[10];//数码桶内数有多少
void sort(int* arr, int start, int end) {int max_value = arr[start];for (int i = start; i <= end; i++) {if (arr[i] > max_value) {max_value = arr[i];}}int max_length = 0;while (max_value > 0) {max_length++;max_value /= 10;}if (max_length == 0) return;//如果都是0for (int i = 0, base = 1; i < max_length; i++, base *= 10) {//对每一位进行排序for (int j = start; j <= end; j++) {int digit = arr[j] / base % 10;//存入某位数码为digit的桶buckets[digit][elements_in_bucket[digit]] = arr[j];//桶内数目elements_in_bucket[digit]++;}int index = start;for (int j = 0; j < 10; j++) {//遍历数码桶if (elements_in_bucket[j] != 0) {for (int k = 0; k < elements_in_bucket[j]; k++) {arr[index++] = buckets[j][k];}}elements_in_bucket[j] = 0;//}}
}
相关文章:
(含代码)(完工于2023.8.3))
【排序算法略解】(十种排序的稳定性,时间复杂度以及实现思想)(含代码)(完工于2023.8.3)
文章目录 1、冒泡排序/选择排序/插入排序冒泡排序(Bubble Sort)选择排序(Selection Sort)插入排序(Insertion Sort) 2、希尔排序(Shells Sort)3、快速排序(Quick Sort)4、堆排序(Heap Sort)5、归并排序(Merge Sort)6、桶排序/计数排序/基数排序桶排序(Bucket sort)计数排序(Cou…...
学编程实用网站
牛客网:面试刷题和面试经验分享的网站牛客网 - 找工作神器|笔试题库|面试经验|实习招聘内推,求职就业一站解决_牛客网 (nowcoder.com)https://www.nowcoder.com/ 慕课网:在线学习 慕课网-程序员的梦工厂 (imooc.com)https://www.imooc.com/ …...

Camunda 7.x 系列【5】 员工请假流程模型
有道无术,术尚可求,有术无道,止于术。 本系列Spring Boot 版本 2.7.9 本系列Camunda 版本 7.19.0 源码地址:https://gitee.com/pearl-organization/camunda-study-demo 文章目录 1. 概述2. 模型设计2.1 基础配置2.2 启动事件2.3 填写请假单2.4 上级领导审批3.5 经理审批3…...
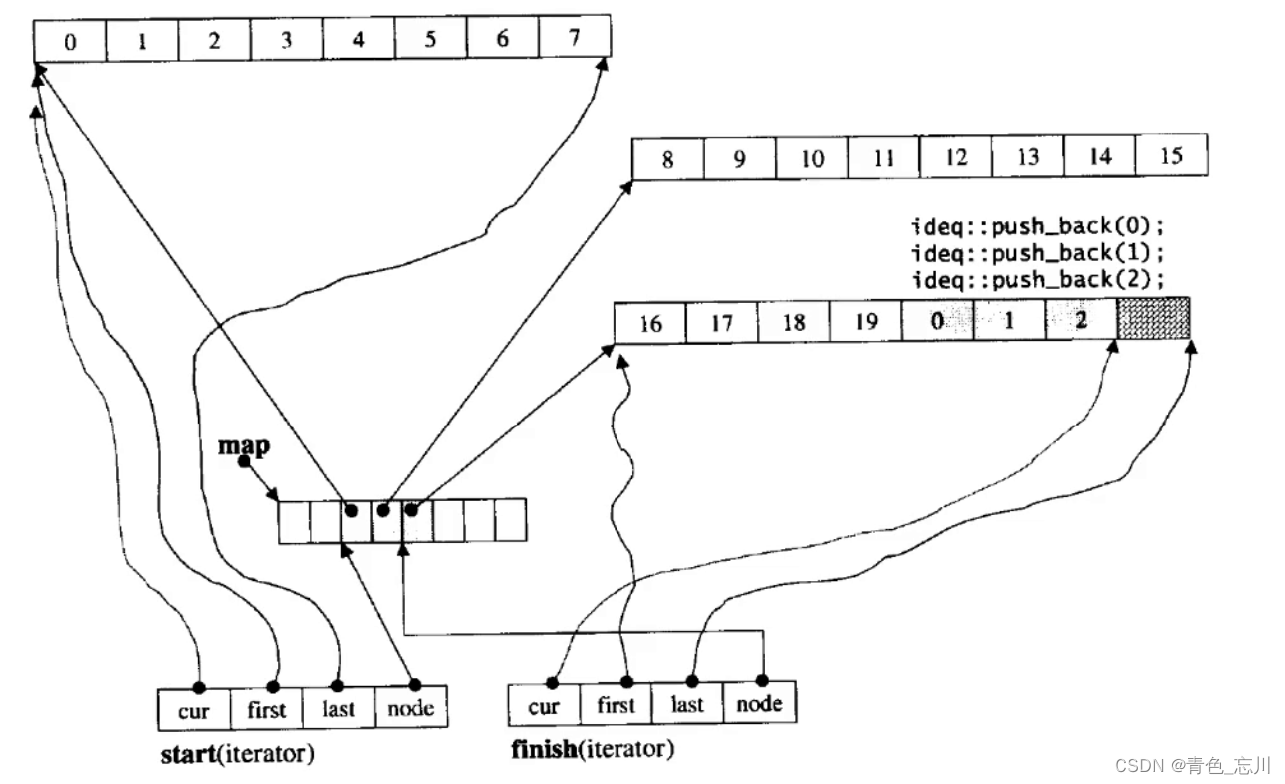
【C++从0到王者】第十七站:手把手教你写一个stack和queue及deque的底层原理
文章目录 一、stack1.利用适配器2.栈的实现 二、queue三、deque1.deque介绍2.deque的接口3.deque的基本使用4.deque的效率5.deque的原理 一、stack 1.利用适配器 我们不可能写了一份数组栈以后,还要在手写一个链式栈,这样显得太冗余了。于是我们可以利…...
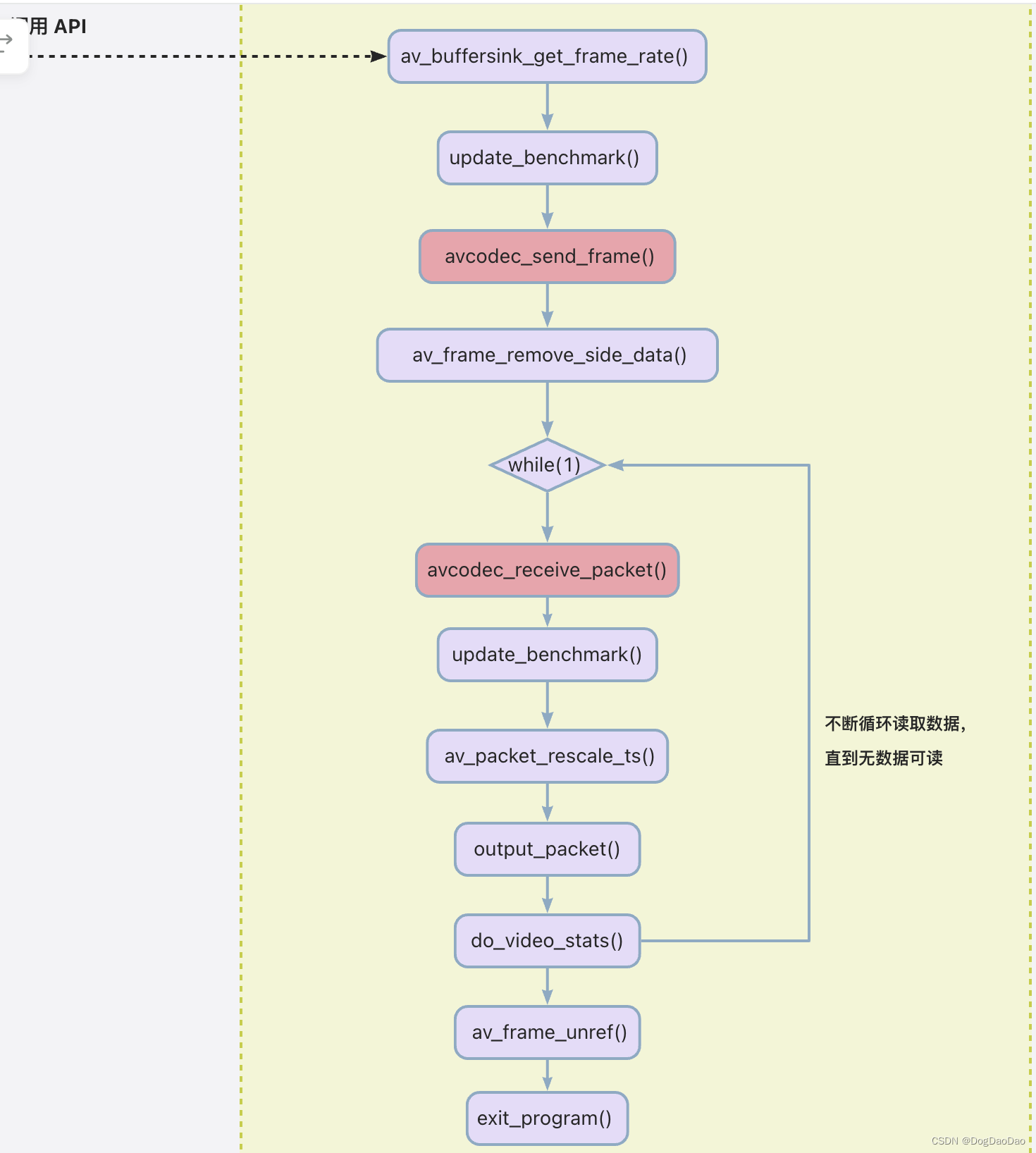
ffmpeg.c源码与函数关系分析
介绍 FFmpeg 是一个可以处理音视频的软件,功能非常强大,主要包括,编解码转换,封装格式转换,滤镜特效。FFmpeg支持各种网络协议,支持 RTMP ,RTSP,HLS 等高层协议的推拉流,…...

GD32F103待机模式与唤醒
GD32F103待机模式与唤醒,本程序使用RTC报警唤醒。 电源管理单元有3种省电模式:睡眠模式,深度睡眠模式和待机模式; 进入待机模式的步骤如下: 若需要RTC闹钟输出,则需要将TAMPER-RTC映射到PC13引脚; 若需要LXTAL晶振32.768KHz&…...
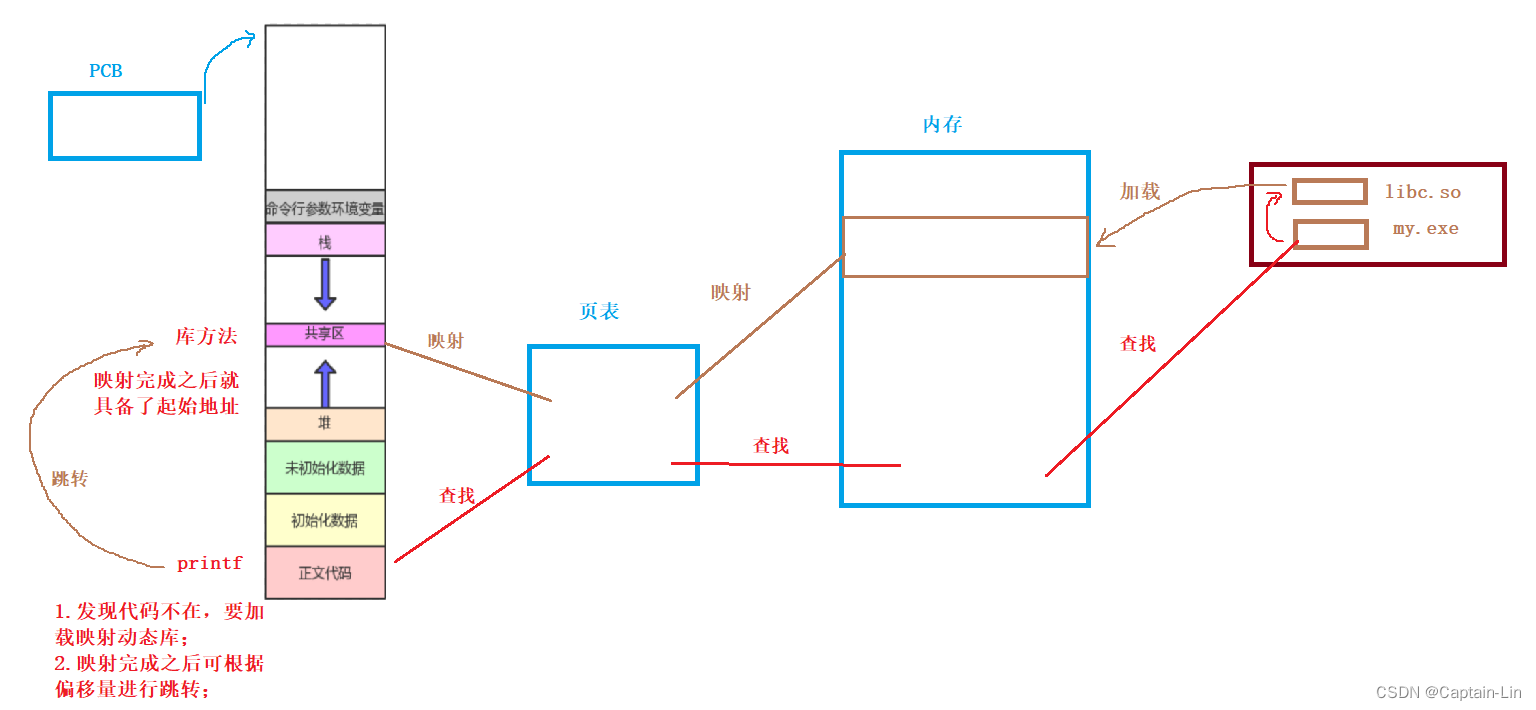
【Linux初阶】基础IO - 动静态库 | 初识、生成、链接、加载
🌟hello,各位读者大大们你们好呀🌟 🍭🍭系列专栏:【Linux初阶】 ✒️✒️本篇内容:动静态库初识,库的含义,静态库的生成与链接,gcc/g默认链接方式,…...

为Git仓库设置签名信息
前言 在首次使用git版本库或创建新的仓库时,需要为其仓库设定管理员和管理员邮箱。 在为仓库添加管理员和邮箱地址时,有以下两种情况: (1)全局模式:首次创建,后面做为默认使用,对当…...

iOS开发Swift开发UI页面链式调用库推荐
首页链接 https://github.com/zhiguangqiao/ChainableUIKit 安装方法 pod ChainableUIKit调用片段 UIButton import ChainableUIKitprivate let button UIButton().chain.setTitleColor(.init(hex: "#9583EB"), state: .normal).setTitle("全部视频",…...
ClickHouse SQL与引擎--基本使用(一)
1.查看所有的数据库 show databases; 2.创建库 CREATE DATABASE zabbix ENGINE Ordinary; ATTACH DATABASE ck_test ENGINE Ordinary;3.创建本地表 CREATE TABLE IF NOT EXISTS test01(id UInt64,name String,time UInt64,age UInt8,flag UInt8 ) ENGINE MergeTree PARTI…...

2023-08-07力扣今日七题-好题
链接: 剑指 Offer 11. 旋转数组的最小数字 154. 寻找旋转排序数组中的最小值 II 题意: 找一个数组里的最小值,这个数组是有非递减数组旋转而来的,旋转n次表示把前n个数移动到数组末尾 解: 很有趣的二分ÿ…...
支持多用户协同的思维导图TeamMapper
什么是 TeamMapper ? TeamMapper 是基于 Mindmapp 开发的用于绘制思维导图的 Web 应用程序。它使得思维导图变得简单,你可以托管并创建您自己的思维导图。与您的团队分享您的思维导图会议并在思维导图上进行协作。 软件特点: 创建࿱…...

【Vue】Parsing error: No Babel config file detected for ... vue
报错 Parsing error: No Babel config file detected for E:\Study\Vue网站\实现防篡改的水印\demo02\src\App.vue. Either disable config file checking with requireConfigFile: false, or configure Babel so that it can find the config files. …...

2023-08-07力扣今日五题
链接: 剑指 Offer 53 - II. 0~n-1中缺失的数字 题意: 如题 解: 长度n的递增数组里,要找0到n中没出现的那个数字,那么出现的下标是0到n-1,一一对应即可,都出现了就是n没有 实际…...
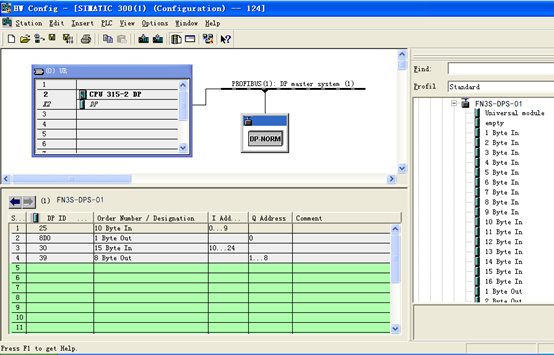
ETHERCAT转PROFIBUS连接到300plc的配置方法
由于捷米JM-DP-ECT,是自主研发的一款PROFIBUS从站功能的通讯网关,它的主要功能是将ETHERCAT设备接入到PROFIBUS网络中生产环境比较复杂有多个设备采用不同的协议这极大的阻碍了,各个设备的数据互通。 JM-DP-ECT这个小小的网关可不简单&#x…...
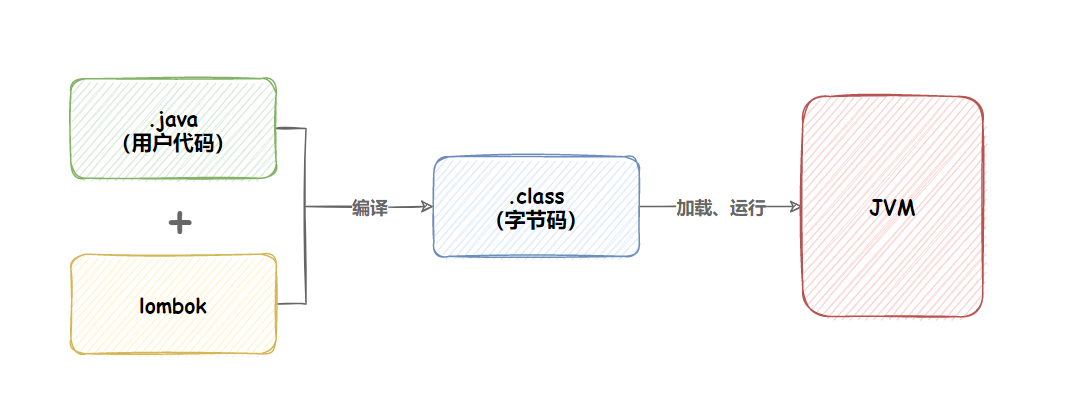
Spring Boot配置文件与日志文件
1. Spring Boot 配置文件 我们知道, 当我们创建一个Spring Boot项目之后, 就已经有了配置文件存在于目录结构中. 1. 配置文件作用 整个项目中所有重要的数据都是在配置文件中配置的,比如: 数据库的连接信息 (包含用户名和密码的设置) ;项目的启动端口;第三方系统的调…...
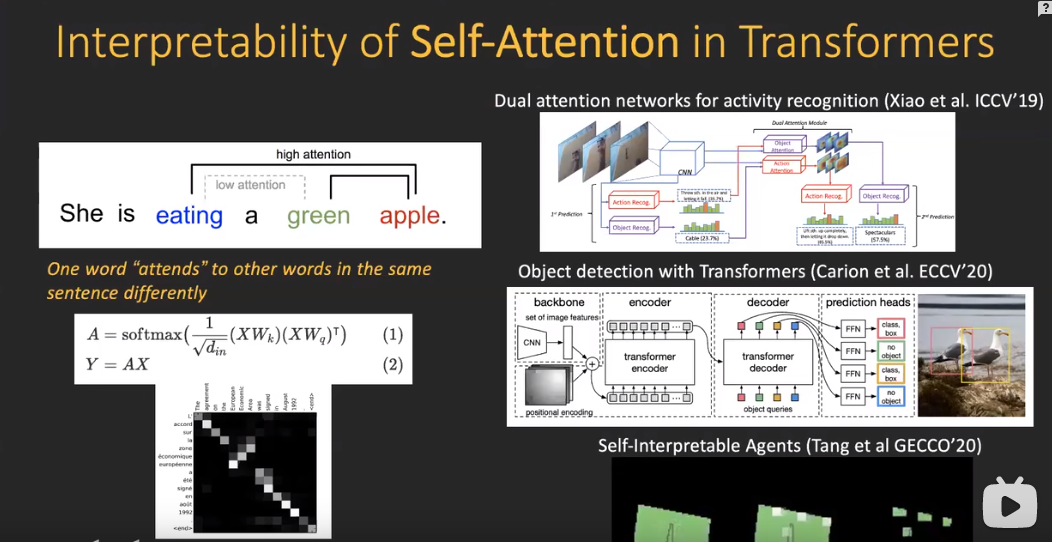
可解释性分析的一些类别(草稿)(视觉)
目录 1.交互性解释 2. 本身具有解释性的模型 3.如何将可解释性分析应用到生成模型 参考文献 视觉领域从2020年开始可以分为两块,一个是图像分类,一个是图像生成。 图像分类:输入一张图片,输出语义标签,就是这张图…...
HTTPS-RSA握手
RSA握手过程 HTTPS采用了公钥加密和对称加密结合的方式进行数据加密和解密 RSA握手是HTTPS连接建立过程中的一个关键步骤,用于确保通信双方的身份验证和生成对称加密所需的密钥 通过RSA握手过程,客户端和服务器可以协商出一个共享的对称密钥,…...

bigemap国土管理行业应用
由于国营企业单位,管理土地,必须要有这样的软件套图 客户之前用的谷歌,后来不能访问了,通过其他途径搜索到我们 客户使用软件一般都用于套坐标以及空间规划图,方便于项目选址和居民建房报建在卫星图上找到用地范围&am…...

深入探索 Splashtop Enterprise 的潜力
在当今高度技术化的环境中,远程访问解决方案已成为无数组织的支柱。远程访问解决方案缩短了员工与工作之间的地理差距,提高了工作的效率和灵活性,促进形成了无缝的工作体验。在众多远程访问解决方案中,Splashtop Enterprise 作为远…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...
