2023-08-07力扣今日七题-好题
链接:
剑指 Offer 11. 旋转数组的最小数字
154. 寻找旋转排序数组中的最小值 II
题意:
找一个数组里的最小值,这个数组是有非递减数组旋转而来的,旋转n次表示把前n个数移动到数组末尾
解:
很有趣的二分,由于是非递减数组旋转而来,所以最小值往右一定小于等于最小值左侧,可以以此进行二分
如果这个数字大于nums[r],那么他一定属于最小值左侧,小于nums[r]一定属于右侧
But:唯一要注意等于的情况,因为存在重复数字,所以有可能 所有/大部分数字都是同一个,则时候无法判断在最小值左侧还是右侧,只能减小右端点。也不能和左端点比较/增大左端点,因为有可能是旋转n次转回了原数组(前面一段一个是个非递减序列,一开始的L=0算是前面一段的最小值)
一边是Easy一边是Hard是吧,真有你的嗷leetcode(大概是暴力能过的原因=-=)
实际代码:
#include<bits/stdc++.h>
using namespace std;
int findMin(vector<int>& numbers)
{int lg=numbers.size(),l=0,r=lg-1;while(l<r){int mid=l+((r-l)>>1);if(numbers[mid]==numbers[r]) r--;else if(numbers[mid]<numbers[r]) r=mid;else l=mid+1;}return numbers[l];
}
int minArray(vector<int>& numbers)
{int lg=numbers.size(),l=0,r=lg-1;while(l<r){int mid=l+((r-l)>>1);if(numbers[mid]==numbers[r]) r--;else if(numbers[mid]<numbers[r]) r=mid;else l=mid+1;}return numbers[l];
}
int main()
{vector<int> numbers;int num;while(cin>>num) numbers.push_back(num);int ans=minArray(numbers);cout<<ans<<endl;return 0;
}
限制:
n == numbers.length1 <= n <= 5000-5000 <= numbers[i] <= 5000numbers 原来是一个升序排序的数组,并进行了 1 至 n 次旋转
相关文章:

2023-08-07力扣今日七题-好题
链接: 剑指 Offer 11. 旋转数组的最小数字 154. 寻找旋转排序数组中的最小值 II 题意: 找一个数组里的最小值,这个数组是有非递减数组旋转而来的,旋转n次表示把前n个数移动到数组末尾 解: 很有趣的二分ÿ…...
支持多用户协同的思维导图TeamMapper
什么是 TeamMapper ? TeamMapper 是基于 Mindmapp 开发的用于绘制思维导图的 Web 应用程序。它使得思维导图变得简单,你可以托管并创建您自己的思维导图。与您的团队分享您的思维导图会议并在思维导图上进行协作。 软件特点: 创建࿱…...

【Vue】Parsing error: No Babel config file detected for ... vue
报错 Parsing error: No Babel config file detected for E:\Study\Vue网站\实现防篡改的水印\demo02\src\App.vue. Either disable config file checking with requireConfigFile: false, or configure Babel so that it can find the config files. …...

2023-08-07力扣今日五题
链接: 剑指 Offer 53 - II. 0~n-1中缺失的数字 题意: 如题 解: 长度n的递增数组里,要找0到n中没出现的那个数字,那么出现的下标是0到n-1,一一对应即可,都出现了就是n没有 实际…...
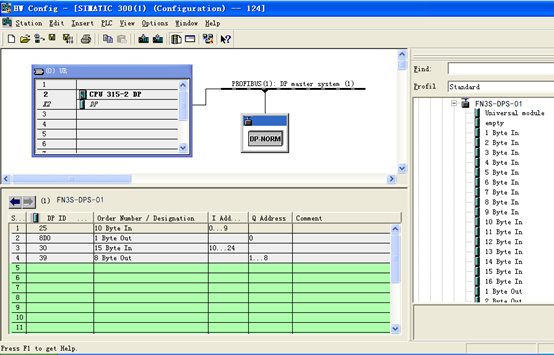
ETHERCAT转PROFIBUS连接到300plc的配置方法
由于捷米JM-DP-ECT,是自主研发的一款PROFIBUS从站功能的通讯网关,它的主要功能是将ETHERCAT设备接入到PROFIBUS网络中生产环境比较复杂有多个设备采用不同的协议这极大的阻碍了,各个设备的数据互通。 JM-DP-ECT这个小小的网关可不简单&#x…...
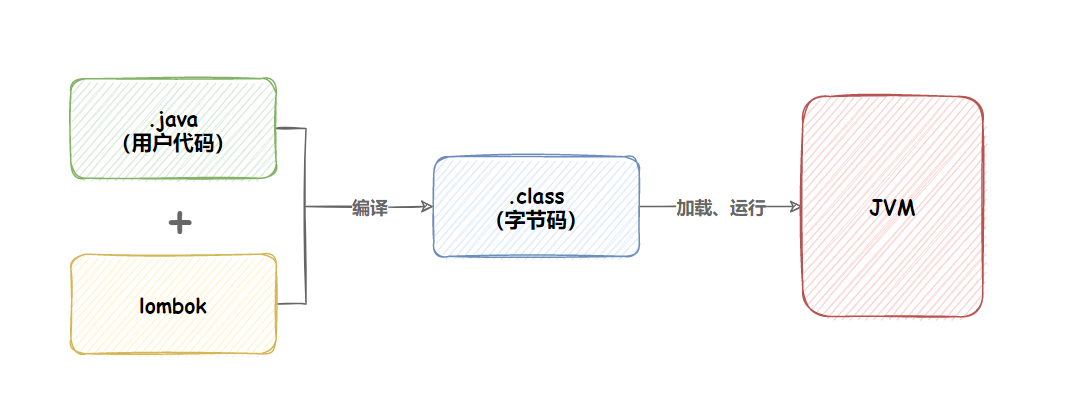
Spring Boot配置文件与日志文件
1. Spring Boot 配置文件 我们知道, 当我们创建一个Spring Boot项目之后, 就已经有了配置文件存在于目录结构中. 1. 配置文件作用 整个项目中所有重要的数据都是在配置文件中配置的,比如: 数据库的连接信息 (包含用户名和密码的设置) ;项目的启动端口;第三方系统的调…...
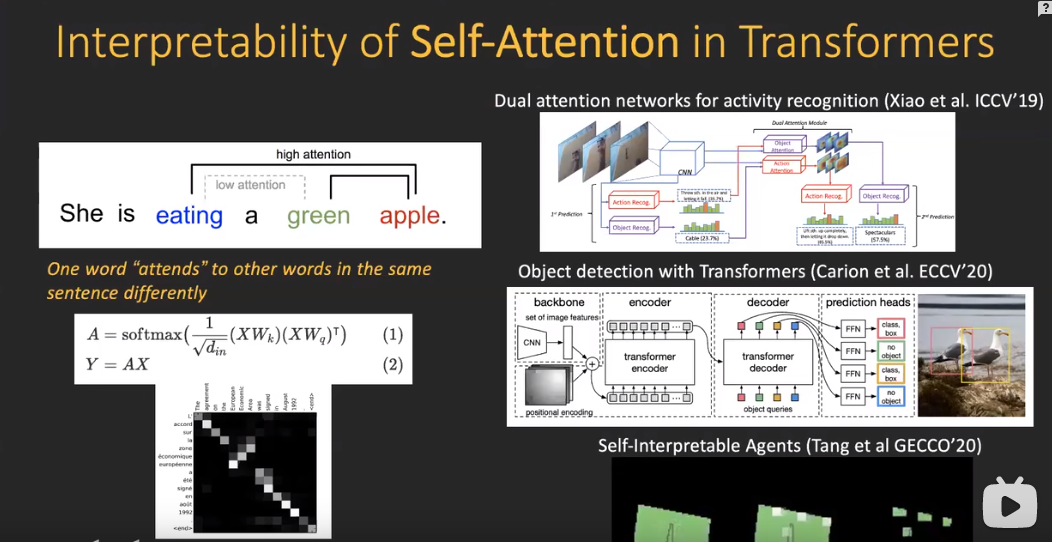
可解释性分析的一些类别(草稿)(视觉)
目录 1.交互性解释 2. 本身具有解释性的模型 3.如何将可解释性分析应用到生成模型 参考文献 视觉领域从2020年开始可以分为两块,一个是图像分类,一个是图像生成。 图像分类:输入一张图片,输出语义标签,就是这张图…...
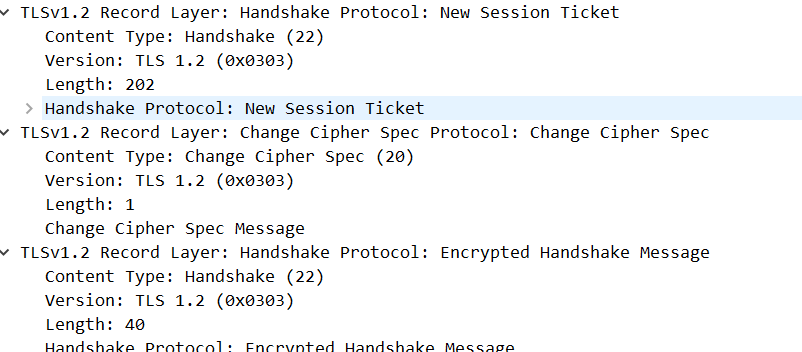
HTTPS-RSA握手
RSA握手过程 HTTPS采用了公钥加密和对称加密结合的方式进行数据加密和解密 RSA握手是HTTPS连接建立过程中的一个关键步骤,用于确保通信双方的身份验证和生成对称加密所需的密钥 通过RSA握手过程,客户端和服务器可以协商出一个共享的对称密钥,…...

bigemap国土管理行业应用
由于国营企业单位,管理土地,必须要有这样的软件套图 客户之前用的谷歌,后来不能访问了,通过其他途径搜索到我们 客户使用软件一般都用于套坐标以及空间规划图,方便于项目选址和居民建房报建在卫星图上找到用地范围&am…...

深入探索 Splashtop Enterprise 的潜力
在当今高度技术化的环境中,远程访问解决方案已成为无数组织的支柱。远程访问解决方案缩短了员工与工作之间的地理差距,提高了工作的效率和灵活性,促进形成了无缝的工作体验。在众多远程访问解决方案中,Splashtop Enterprise 作为远…...

创建型模式-单例模式
文章目录 一、创建型模式1. 单例设计模式1.1 单例模式的结构1.2 单例模式的实现(1)饿汉式-方式1(静态变量方式)(2)饿汉式-方式2(静态代码块方式)(3)懒汉式-方…...
2. Linux安装Git
yum安装 查看版本 版本太低,所以我们采用自己上传编译的方式进行 删除已安装的git yum remove git 下载最新安装包,并上传到服务器文件夹下 上传,解压 5.安装编译需要的依赖 yum install curl-devel expat-devel gettext-devel openssl-…...
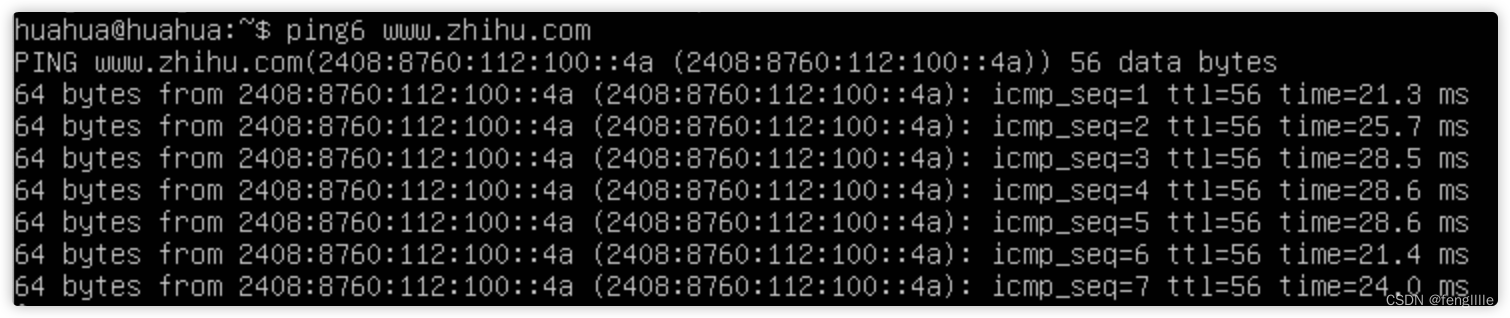
检查网站是HTTP那种协议与获取域名的ipv6地址
前言 最近在做HTTPS的应用,可能需要使用ipv6的地址做SLB,但是怎么检查配置正确,总不能每次都看日志吧,实际上客户端也很容易查看,总结工作经验。 检查HTTP协议版本 笔者想到了使用浏览器方式,或者抓包&a…...
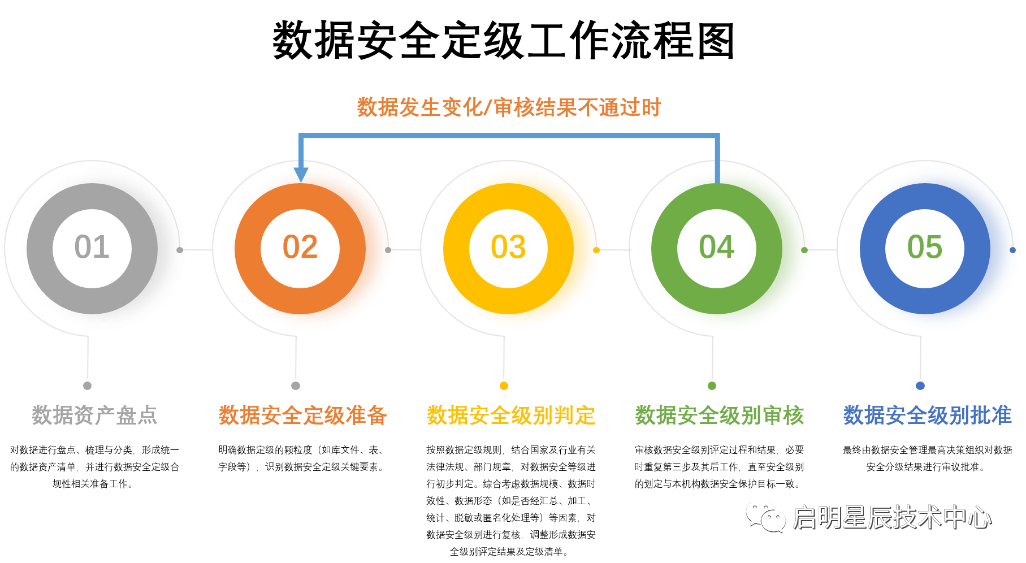
【转】金融行业JR/T0197-2020《金融数据安全 数据安全分级指南》解读
原文链接:金融行业JR/T0197-2020《金融数据安全 数据安全分级指南》解读 《金融数据安全 数据安全分级指南》 解 读 随着IT技术的发展,银行的基础业务、核心流程等众多事务和活动都运营在信息化基础之上,金融机构运行过程中产生了大量的数字…...

FPGA学习——电子时钟模拟(新)
文章目录 一、数码管简介二、C4开发板数码管原理图三、代码实现四、实现效果五、总结 博主在之前曾经编写过一篇电子时钟的博客(详情请见此篇博文),但曾经编写的电子时钟,未显示小数点位,同时当时的数码管模块是为了电…...
一文读懂快速开发平台
一、开发平台是什么? 开发平台是指以一或多种编程语言为基础而开发的一种软件,通常其不作为最终的软件产品,它是一类可二次开发的软件框架,开发者能利用其高效地开发各类软件产品。 在利用开发平台进行开发工作时,可摒…...

Docker实战-操作Docker容器实战(二)
导语 上篇分享中,我们介绍了关于如何创建容器、如何启动容器、如何停止容器。这篇我们来分享一下如何操作容器。 如何进入容器 可以通过使用-d参数启动容器后会进入后台运行,用户无法查看容器中的信息,无法对容器中的信息进行操作。 这个时候如果我们需要进入容器对容器…...
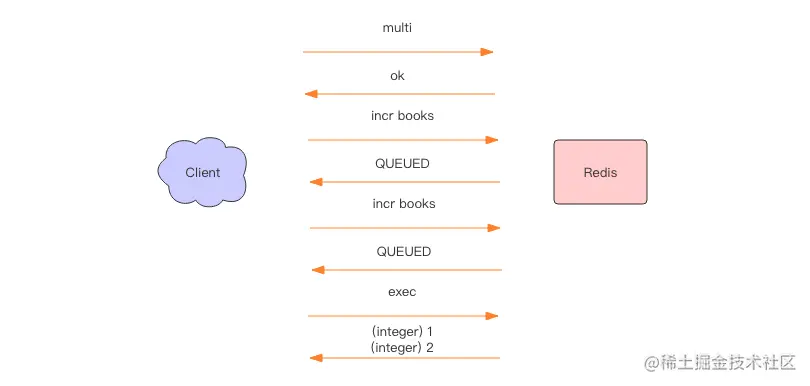
redis原理 5:同舟共济 —— 事务
为了确保连续多个操作的原子性,一个成熟的数据库通常都会有事务支持,Redis 也不例外。Redis 的事务使用非常简单,不同于关系数据库,我们无须理解那么多复杂的事务模型,就可以直接使用。不过也正是因为这种简单性&#…...

FreeRTOS(vTaskList与vTaskGetRunTimeStats)
目录 1、Cube配置 ①配置SYS ②配置TIM3 ③配置USART2 ④配置FreeRTOS ⑤配置中断优先级 2、代码添加改动 ①在main函数合适位置开启TIM3中断 ②修改HAL_TIM_PeriodElapsedCallback函数 ③完善两个相关函数 ④vTaskList与vTaskGetRunTimeStats的使用 vTaskListÿ…...
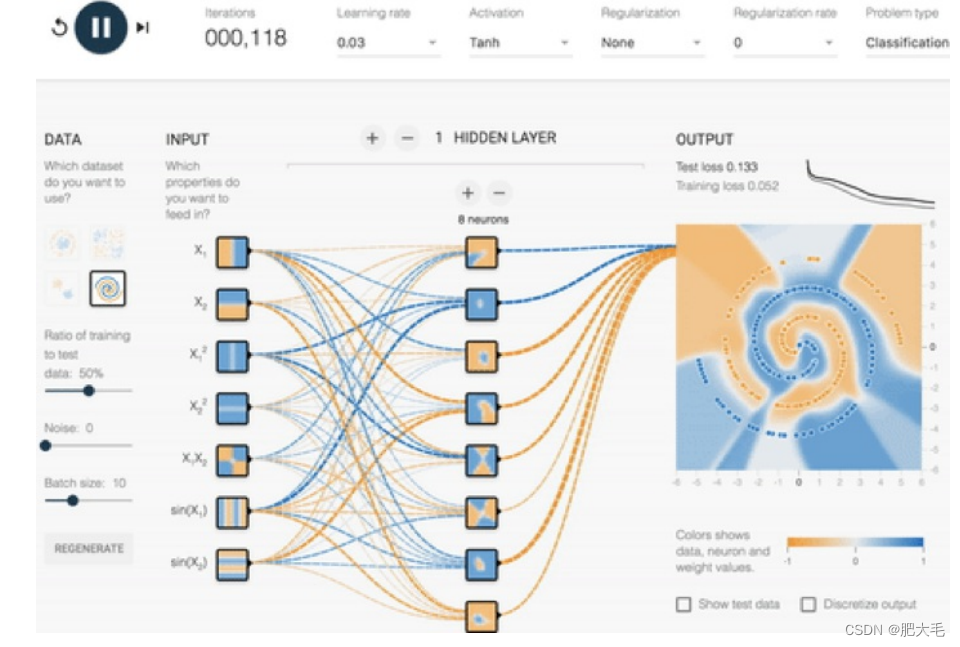
机器学习---概述(二)
文章目录 1.模型评估1.1 分类模型评估1.2 回归模型评估 2. 拟合2.1 欠拟合2.2 过拟合2.3 适当拟合总结: 3.深度学习3.1层次(Layers):3.2 神经元(Neurons):3.3 总结 1.模型评估 模型评估是机器学…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...
