【蓝桥日记⑤】2014第五届省赛(软件类)JavaA组❆答案解析
【蓝桥日记⑤】2014第五届省赛(软件类)JavaA组☃答案解析
文章目录
- 【蓝桥日记⑤】2014第五届省赛(软件类)JavaA组☃答案解析
- 1、猜年龄
- 2、李白打酒
- 3、神奇算式
- 4、写日志
- 5、锦标赛
- 6、六角填数
- 7、绳圈
- 8、兰顿蚂蚁
- 9、斐波那契
- 10、波动数列
1、猜年龄
解法:暴力枚举
package fiveSession;/*** 2014第五届 1、猜年龄 ***/
public class test1 {public static void main(String[] args) {int age1 = 0, age2 = 0;boolean find = false;for (int i = 1; i < 50; i++) {for (int j = i + 1; j < i + 9; j++) {if (i * j == 6 * (i + j)) {age1 = i;age2 = j;find = true;break;}}if (find) break;}System.out.println(age1);}
}
答案:
10
2、李白打酒
解法:递归
package fiveSession;/*** 2014第五届 2、李白打酒 ***/
public class test2 {public static void main(String[] args) {int wine = 2;int shop = 5, flower = 10;int res = f(wine, shop, flower);System.out.println(res);}private static int f(int wine, int shop, int flower) {if (shop < 0 || flower < 0) return 0;if (wine == 0 && (shop != 0 || flower != 0)) return 0;if (wine == 0 && shop == 0 && flower == 0) return 1;int res = f(wine * 2, shop - 1, flower);res += f(wine - 1, shop, flower - 1);return res;}
}
递归二
package fiveSession;/*** 2014第五届 2、李白打酒 ***/
public class test2 {static int res = 0;public static void main(String[] args) {int wine = 2;int shop = 5, flower = 10 - 1;f(wine, shop, flower);System.out.println(res);}private static void f(int wine, int shop, int flower) {if (wine == 1 && shop == 0 && flower == 0) {res++;return;}if (shop > 0) f(wine * 2, shop - 1, flower);if (flower > 0) f(wine - 1, shop, flower - 1);}
}
答案:
14
3、神奇算式
解法:暴力枚举
package fiveSession;import java.util.Arrays;/*** 2014第五届 3、神奇算式 ***/
public class test3 {public static void main(String[] args) {int res = 0;for (int i = 1; i < 10; i++) {for (int j = 0; j < 10; j++) {if (i == j) continue;for (int k = 0; k < 10; k++) {if (i == k || j == k) continue;for (int p = 0; p < 10; p++) {if (i == p || j == p || k == p) continue;int src = i * 1000 + j * 100 + k * 10 + p;if (j != 0) {res += check(src, i * (j * 100 + k * 10 + p));}if (k != 0 && (i * 10 + j) < (k * 10 + p)) {res += check(src, (i * 10 + j) * (k * 10 + p));}}}}}System.out.println(res);}public static int check(int src, int r2) {String s1 = String.valueOf(src);String s2 = String.valueOf(r2);char[] cs1 = s1.toCharArray();char[] cs2 = s2.toCharArray();Arrays.sort(cs1);Arrays.sort(cs2);if (new String(cs1).equals(new String(cs2))) return 1;return 0;}
}
答案:
12
4、写日志
解法:找规律
package fiveSession;/*** 2014第五届 4、写日志 ***/
public class test4 {private static int n = 1;public static void write(String msg) {String filename = "t" + n + ".log";n = (n % 3) + 1;System.out.println(filename + "," + msg);}public static void main(String[] args) {for (int i = 0; i < 15; i++) write("a");}
}
答案:
(n % 3) + 1
5、锦标赛
package fiveSession;/*** 2014第五届 5、锦标赛 ***/
public class test5 {static void f(int[] a) {int n = 1;while (n < a.length) n *= 2;int[] b = new int[2 * n - 1];for (int i = 0; i < n; i++) {if (i < a.length)b[n - 1 + i] = i;elseb[n - 1 + i] = -1;}//从最后一个向前处理for (int i = b.length - 1; i > 0; i -= 2) {if (b[i] < 0) {if (b[i - 1] >= 0)b[(i - 1) / 2] = b[i - 1];elseb[(i - 1) / 2] = -1;} else {if (a[b[i]] > a[b[i - 1]])b[(i - 1) / 2] = b[i];elseb[(i - 1) / 2] = b[i - 1];}}//输出树根System.out.println(b[0] + ":" + a[b[0]]);//值等于根元素的需要重新pkpk(a, b, 0, b[0]);//再次输出树根System.out.println(b[0] + ":" + a[b[0]]);}static void pk(int[] a, int[] b, int k, int v) {//if(k>b.length) return;int k1 = k * 2 + 1;int k2 = k1 + 1;if (k1 >= b.length || k2 >= b.length) {// 此处将 叶子结点为最大值的 下标b[k]抹去,置为-1 b[k] = -1; //(要是我我会该行代码设为考点~(@^_^@)~)return;}if (b[k1] == v)pk(a, b, k1, v);elsepk(a, b, k2, v);//重新比较if (b[k1] < 0) {if (b[k2] >= 0)b[k] = b[k2];elseb[k] = -1;return;}if (b[k2] < 0) {if (b[k1] >= 0)b[k] = b[k1];elseb[k] = -1;return;}if (a[b[k1]]>a[b[k2]])b[k] = b[k1];elseb[k] = b[k2];}public static void main(String[] args) {int[] a = {54, 55, 18, 16, 122, 255, 30, 9, 58, 66};f(a);}
}
答案:
a[b[k1]]>a[b[k2]]
6、六角填数
解法:全排列+剪枝
package fiveSession;/*** 2014第五届 6、六角填数 ***/
public class test6 {static int[] a = {2, 4, 5, 6, 7, 9, 10, 11, 12};public static void main(String[] args) {backtrack(0, a.length);}private static void backtrack(int begin, int end) {if (begin == 6 && 8 + a[0] + a[1] + a[2] != 1 + a[0] + a[3] + a[5]) return;if (begin == 7 && 8 + a[0] + a[1] + a[2] != 8 + a[3] + a[6] + 3) return;if (begin == end) {if (8 + a[0] + a[1] + a[2] != a[5] + a[6] + a[7] + a[8]) return;if (8 + a[0] + a[1] + a[2] != a[2] + a[4] + a[7] + 3) return;if (8 + a[0] + a[1] + a[2] != 1 + a[1] + a[4] + a[8]) return;System.out.println(a[3]);}for (int i = begin; i < end; i++) {int t = a[begin]; a[begin] = a[i]; a[i] = t;backtrack(begin + 1, end);t = a[begin]; a[begin] = a[i]; a[i] = t;}}
}
答案:
10
7、绳圈
解法:动态规划
绳圈组合数:自成一圈+加入前一组合(2个头+i -1个分割点)
令C[i]表示i个绳的组合数,则有
C[i]=c[i−1]+C[i−1]∗(i−1)∗2=C[i−1]∗(2i−1)C[i] = c[i -1] + C[i - 1] *(i - 1) * 2 = C[i-1]*(2i-1) C[i]=c[i−1]+C[i−1]∗(i−1)∗2=C[i−1]∗(2i−1)
令F[i][j]表示i个绳组j个圈的概率,则有
F[i][j]=F[i−1][j−1]∗C[i−1]+F[i−1][j]∗C[i−1]∗(i−1)∗2C[i]F[i][j]=\frac{F[i-1][j-1]*C[i-1]+F[i-1][j]*C[i-1]*(i-1)*2}{C[i]} F[i][j]=C[i]F[i−1][j−1]∗C[i−1]+F[i−1][j]∗C[i−1]∗(i−1)∗2
联立两式约分有
F[i][j]=F[i−1][j−1]+F[i−1][j]∗(i−1)∗22i−1F[i][j]=\frac{F[i-1][j-1]+F[i-1][j]*(i-1)*2}{2i-1} F[i][j]=2i−1F[i−1][j−1]+F[i−1][j]∗(i−1)∗2
package fiveSession;/*** 2014第五届 7、绳圈 ***/
public class test7 {public static void main(String[] args) {double[][] f = new double[101][101];f[1][1] = 1;for (int rope = 2; rope <= 100; rope++) {f[rope][1] = f[rope - 1][1] * (rope - 1) * 2 / (2 * rope - 1);for (int circle = 2; circle <= rope; circle++) {f[rope][circle] = (f[rope - 1][circle - 1] + f[rope - 1][circle] * (rope - 1) * 2) / (2 * rope - 1);}}int ans = 0;double maxVal = 0.0;for (int circle = 1; circle <= 100; circle++) {if (f[100][circle] > maxVal) {maxVal = f[100][circle];ans = circle;}}System.out.println(ans);}
}
答案:
3
8、兰顿蚂蚁
解法:方向模拟
package fiveSession;import java.util.Scanner;/*** 2014第五届 8、兰顿蚂蚁 ***/
public class test8 {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int m = sc.nextInt();int n = sc.nextInt();int[][] g = new int[m][n];for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {g[i][j] = sc.nextInt();}}int x = sc.nextInt();int y = sc.nextInt();String s = sc.next();int d = getD(s);int k = sc.nextInt();// 方向: 上右下左int[][] dirs = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};for (int i = 1; i <= k; i++) {if (g[x][y] == 0) {d = (d + 3) % 4;g[x][y] = 1;} else {d = (d + 1) % 4;g[x][y] = 0;}x = x + dirs[d][0];y = y + dirs[d][1];}System.out.println(x + " " + y);}private static int getD(String s) {if (s.equals("U")) return 0;if (s.equals("R")) return 1;if (s.equals("D")) return 2;return 3;}
}
9、斐波那契
解法一:暴力法(4/7)
package fiveSession;import java.util.Scanner;/*** 2014第五届 9、斐波那契,暴力法1 ***/
public class test9 {public static void main(String[] args) {Scanner sc = new Scanner(System.in);long n = sc.nextLong();long m = sc.nextLong();long p = sc.nextLong();long sum = 1;long t = 0, f1 = 0, f2 = 1, mMod = 0;for (long i = 2; i <= n; i++) {t = f2 + f1;f1 = f2;f2 = t;sum += t;if (i == m) mMod = t;}if (m > n) {for (long i = n + 1; i <= m; i++) {t = f2 + f1;f1 = f2;f2 = t;}mMod = f2;}System.out.println(sum % mMod % p);}
}
解法二:公式定理+矩阵运算
我这个水平,能暴力就暴力,现在记公式定理性价比不高,推理构造的到时可以深究一下。
有兴趣的可以看一下参考:从蓝桥杯来谈Fibonacci数列
10、波动数列
解法一:枚举首项+dfs(2/8)
x x+a x+2a x+3a ··· x+(n-1)a s = nx + n(n-1)a/2
x x-b x-2b x-3b ··· x-(n-1)b s = nx - n(n-1)b/2
通过上式可以求出首项x的范围
package fiveSession;import java.util.Scanner;/*** 2014第五届 10、波动数列 ***/
public class test10 {static int n, s, a, b;static long ans;static final int MOD = (int)1e8 + 7;public static void main(String[] args) {Scanner sc = new Scanner(System.in);n = sc.nextInt();s = sc.nextInt();a = sc.nextInt();b = sc.nextInt();sc.close();// x x+a x+2a x+3a ··· x+(n-1)a s = nx + n(n-1)a/2//x x-b x-2b x-3b ··· x-(n-1)b s = nx - n(n-1)b/2int minX = (s - (n - 1) * n * a / 2) / n;int maxX = (s + (n - 1) * n * b / 2) / n;for (int x = minX; x <= maxX; x++) {dfs(x, 1, x);}System.out.println(ans);}private static void dfs(int x, int cnt, int sum) {if (cnt == n) {if (sum == s) {ans++;if (ans > MOD) ans %= MOD;}return;}dfs(x + a, cnt + 1, sum + x + a);dfs(x - b, cnt + 1, sum + x - b);}
}
优化:枚举a,b的数目+dfs(2/8)
package fiveSession;import java.util.Scanner;/*** 2014第五届 10、波动数列, 优化枚举 ***/
public class test10_2 {static int n, s, a, b;static long ans;static final int MOD = (int)1e8 + 7;public static void main(String[] args) {Scanner sc = new Scanner(System.in);n = sc.nextInt();s = sc.nextInt();a = sc.nextInt();b = sc.nextInt();sc.close();// x x+p x+2p x+3p ··· x+(n-1)p s = nx + n(n-1)p/2// t = n(n-1)/2// 若a的数目为ta, 则b数目为tbint t = n * (n - 1) / 2;long minX = (s - a * t) / n;long maxX = (s + b * t) / n;for (long x = minX; x <= maxX; x++) {for (long ta = 0; ta <= t; ta++) {// 减少对x的枚举long curSum = x * n + ta * a - (t - ta) * b;if (curSum == s) dfs(x, 1, x);}}System.out.println(ans);}private static void dfs(long x, int cnt, long sum) {if (cnt == n) {if (sum == s) {ans++;if (ans > MOD) ans %= MOD;}return;}dfs(x + a, cnt + 1, sum + x + a);dfs(x - b, cnt + 1, sum + x - b);}
}
解法二:动态规划,求a和b的组合数(7/10)
package fiveSession;import java.util.Scanner;/*** 2014第五届 10、波动数列, 动态规划 ***/
public class test10_3{static int n, s, a, b;static long ans;static final int MOD = (int)1e8 + 7;public static void main(String[] args) {Scanner sc = new Scanner(System.in);n = sc.nextInt();s = sc.nextInt();a = sc.nextInt();b = sc.nextInt();sc.close();dpMethod();System.out.println(ans);}private static void dpMethod() {int t = n * (n - 1) / 2;// dp[i][j]表示用前i个数组成值j的组合数方法int[][] dp = new int[n][t + 1];dp[0][0] = 1;for (int i = 0; i < n; i++) dp[i][0] = 1;for (int i = 1; i < n; i++) {for (int j = 1; j <= t; j++) {if (i > j) {dp[i][j] = dp[i - 1][j];} else {dp[i][j] = dp[i - 1][j] + dp[i - 1][j - i];}dp[i][j] %= MOD;}}for (int ta = 0; ta <= t; ta++) {if ((s - ta * a + (t - ta) * b) % n == 0) {ans = (ans + dp[n - 1][ta]) % MOD;}}}
}
优化:动态规划+滚动数组将状态压缩为二维(7/10)
package fiveSession;import java.util.Scanner;/*** 2014第五届 10、波动数列, 动态规划 ***/
public class test10_3{static int n, s, a, b;static long ans;static final int MOD = (int)1e8 + 7;public static void main(String[] args) {Scanner sc = new Scanner(System.in);n = sc.nextInt();s = sc.nextInt();a = sc.nextInt();b = sc.nextInt();sc.close();dpMethod2();System.out.println(ans);}private static void dpMethod2() {int t = n * (n - 1) / 2;// dp[i][j]表示用前i个数组成值j的组合数方法int[][] dp = new int[2][t + 1];dp[0][0] = dp[1][0] = 1;int row = 0;for (int i = 1; i < n; i++) {row = 1 - row;for (int j = 1; j <= t; j++) {if (i > j) {dp[row][j] = dp[1 - row][j];} else {dp[row][j] = dp[1 - row][j] + dp[1 - row][j - i];}dp[row][j] %= MOD;}}for (long ta = 0; ta <= t; ta++) {if ((s - ta * a + (t - ta) * b) % n == 0) {ans = (ans + dp[row][(int)ta]) % MOD;}}}
}
优化:动态规划+状态压缩为一维(10/10)
package fiveSession;import java.util.Scanner;/*** 2014第五届 10、波动数列, 动态规划 ***/
public class test10_3{static int n, s, a, b;static long ans;static final int MOD = (int)1e8 + 7;public static void main(String[] args) {Scanner sc = new Scanner(System.in);n = sc.nextInt();s = sc.nextInt();a = sc.nextInt();b = sc.nextInt();sc.close();dpMethod3();System.out.println(ans);}private static void dpMethod3() {int t = n * (n - 1) / 2;// dp[i][j]表示用前i个数组成值j的组合数方法int[] dp = new int[t + 1];dp[0] = 1;for (int i = 1; i < n; i++) {// 减少j的枚举for (int j = i * (i + 1) / 2; j >= i; j--) {dp[j] = (dp[j] + dp[j - i]) % MOD;}}for (long ta = 0; ta <= t; ta++) {if ((s - ta * a + (t - ta) * b) % n == 0) {ans = (ans + dp[(int)ta]) % MOD;}}}}
这道题目的两种方法的一步步优化真的惊艳到我了!佩服佩服!
参考资料:【蓝桥杯JavaA组】2013-2018年试题讲解(附含C语言版)
总的来说排列组合和动态规划涉及的很多,动态规划永远的伤啊~

相关文章:

【蓝桥日记⑤】2014第五届省赛(软件类)JavaA组❆答案解析
【蓝桥日记⑤】2014第五届省赛(软件类)JavaA组☃答案解析 文章目录【蓝桥日记⑤】2014第五届省赛(软件类)JavaA组☃答案解析1、猜年龄2、李白打酒3、神奇算式4、写日志5、锦标赛6、六角填数7、绳圈8、兰顿蚂蚁9、斐波那契10、波动…...

Leetcode.1139 最大的以 1 为边界的正方形
题目链接 Leetcode.1139 最大的以 1 为边界的正方形 Rating : 1744 题目描述 给你一个由若干 0 和 1 组成的二维网格 grid,请你找出边界全部由 1 组成的最大 正方形 子网格,并返回该子网格中的元素数量。 如果不存在,则返回 0。…...

Bing+ChatGPT 对传统搜索引擎的降维打击
早些时候申请了新版 Bing 的内测资格,终于收到了通过的邮件。 一天的体验之后,我的感受是:当新版 Bing 具备了 ChatGPT 的聊天能力之后,它的能力不论是对传统搜索引擎,还是 ChatGPT 自身,都将是降维打击。 …...
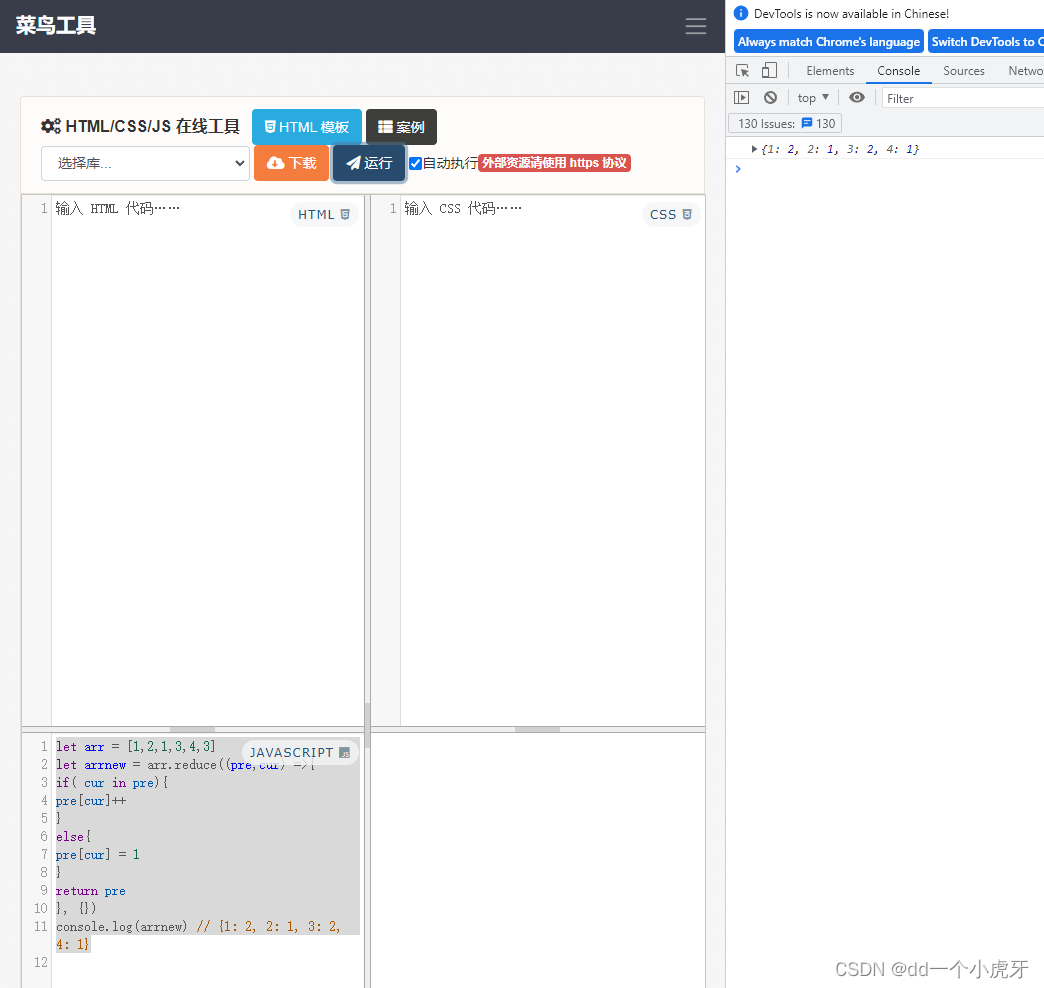
【JS】数组常用方法总结-功能、参数、返回值
数组常用方法总结-功能、参数、返回值 用简单的js示例 运行在线工具:链接: 菜鸟工具 菜鸟工具示意图: pu…...

pytest 单元测试前后置处理
文章目录方法1 setup/teardown方法2 fixture 夹具方法3 conftest.py测试用例执行前后的一些处理动作,也叫夹具。以下介绍使用前后置操作的几种方法。方法1 setup/teardown setup,每个测试用例执行前要进行的处理。 teardown,每个测试用例执行…...
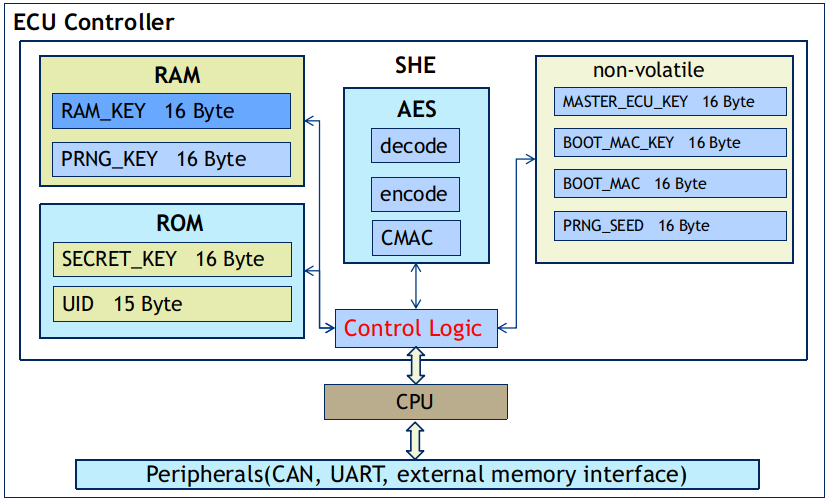
汽车安全硬件扩展 AUTOSAR SHE SecureHardwareExtensions
SHE(Secure Hardware Extension)在车联网中,被应用在车端ECU中负责安全存储与安全计算。是由HIS(由Audi、BMW、Porsche、Volkswagen组成)制定的标准,中文意思“安全硬件扩展”,是对任何给定微控…...
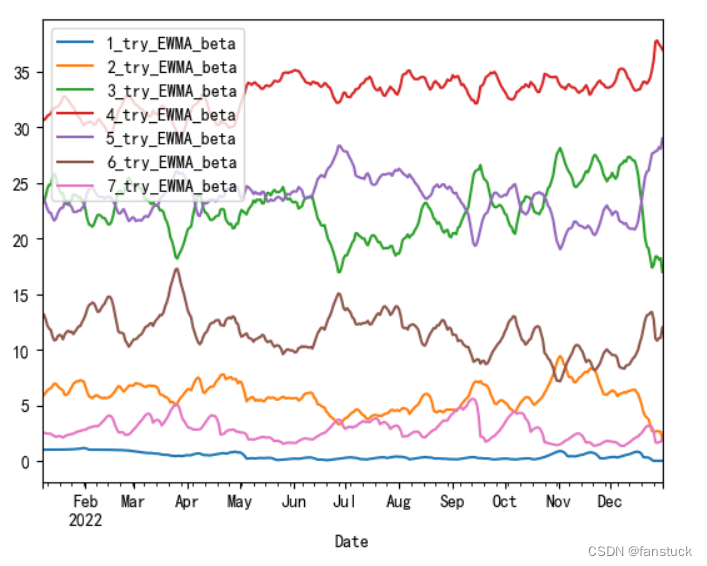
2023年美国大学生数学建模C题:预测Wordle结果建模详解+模型代码
目录 前言 一、题目理解 背景 解析 字段含义: 建模要求 二、建模思路 灰色预测: 编辑 二次指数平滑法: person相关性 只希望各位以后遇到建模比赛可以艾特认识一下我,我可以提供免费的思路和部分源码,以后…...

5、HAL库驱动W25Qxx
一、 SPI通信驱动W25Qxx 1、使用驱动文件快速配置工程代码驱动W25Qxx (此驱动文件只适合W25Qxx 16M及以下型号,因为访问地址位数不同) 注:本次使用SPI的方式进行访问W25Qxx Flash进行数据读写,关于W25Qxx芯片不会做…...
)
git rebase 洐合(变基)
洐合 把一个分支整合到另一个分支的办法有两种:merge(合并) 和 rebase(衍合) 为什么使用? 使提交记录更简洁 三种情况 第一种: 合并多条commit记录 git rebase -i HEAD~合并数量 HEAD~3&a…...

Kubernetes 1.18学习笔记
文章目录一、Kubernetes 概述和架构1、kubernetes 基本介绍2、Kubernetes 功能3、Kubernetes 架构组件4、Kubernetes 核心概念5、Kubernetes 工作原理二、Kubernetes 集群搭建1、系统环境准备1.1 安装要求1.2 系统初始化2、客户端工具kubeadm搭建2.1 安装步骤2.2 安装组件2.3 集…...

AJAX技术
AJAX技术 浏览器是多进程的,简单的说就是,浏览器每打开一个标签页,就相当于创建了一个独立的浏览器进程。但是js是基于单线程的,而这个线程就是浏览器的js引擎,浏览器无论在什么时候都只且只有一个线程在运行JavaScri…...
)
华为OD机试 - 最大排列(JS)
最大排列 题目 给定一组整数,重排序后输出一个最大的整数 输入 数字组合 输出 最大的整数 示例一 输入 10 9输出 910解题思路 我们可以读入一个字符串,将字符串中的单词按照每个单词的字典序长度,字典序从大到小的顺序排序&#x…...
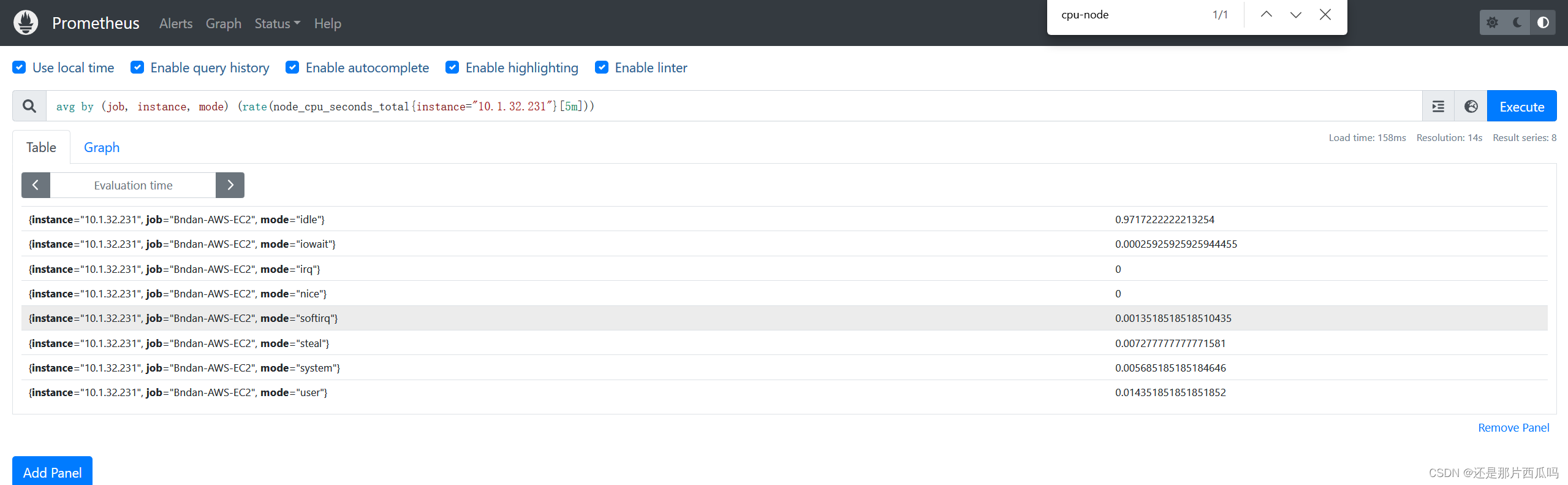
Prometheus Docker安装及监控自身
前提环境: Docker环境 涉及参考文档: 安装Prometheus开始 Prometheusnode_exporter Agent组件 一、部署Prometheus 1、启动容器将文件拷贝出来 docker run -d prom/prometheus2、容器将文件拷贝出来 docker cp 容器ID:/usr/share/prometheus/conso…...

点云处理PCL常用函数与工具
点云处理PCL常用函数与工具 文章目录点云处理PCL常用函数与工具前言一、点云读取与保存数据读取数据保存自定义的点云保存格式二、点云显示点云显示-根据颜色点云显示-根据指定轴数值点云显示-根据指定信息显示多组点云显示三、点云滤波直通滤波统计滤波均匀下采样滤波VoxelGri…...
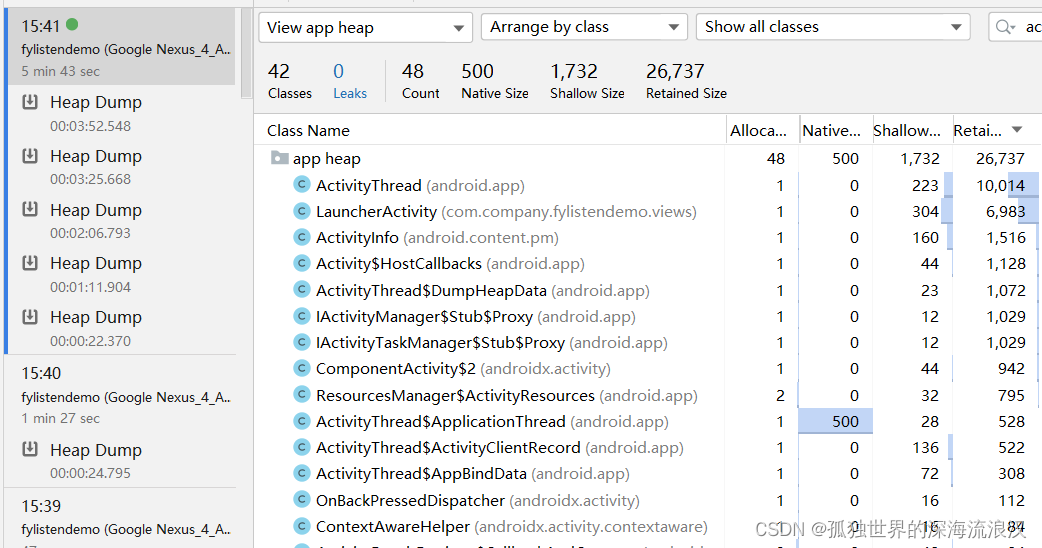
FyListen 在 MVP 架构中的内存优化表现
FyListen 在 MVP 中的内存优化表现 本文只是分享个人开源框架的内存优化测试,你可以直接跳到最后,参考内存泄漏的分析过程! 项目地址: https://github.com/StudyNoteOfTu/fylisten2-alpha1 由于使用到 AOP,所以直接…...
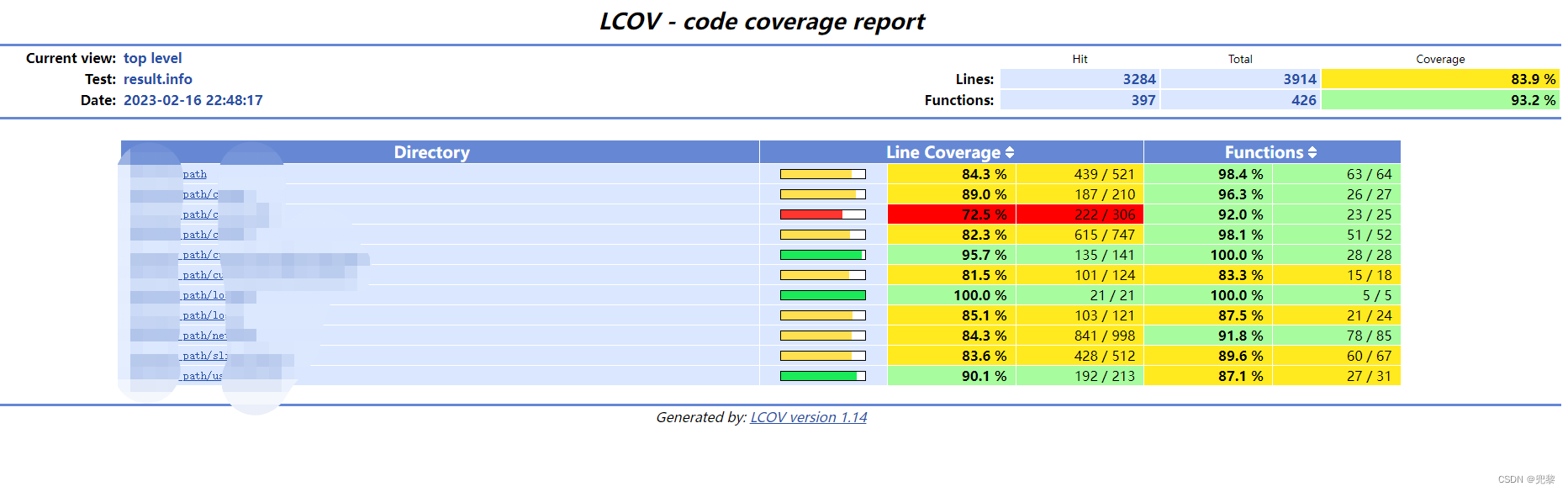
Qt代码单元测试以及报告生成
简介 单元测试是所有测试中最底层的一类测试,是第一个环节,也是最重要的一个环节,是唯一一次有保证能够代码覆盖率达到100%的测试,是整个软件测试过程的基础和前提,单元测试防止了开发的后期因bug过多而失控࿰…...

vscode构建Vue3.0项目(vite,vue-cli)
构建Vue3.0项目构建Vue3.0项目1.使用Vite构建vue项目的方法以及步骤1. 安装vite2. 运行vite vue 项目3.说明2.使用vue-cli构建vue项目的方法以及步骤1.安装全局vue cli —— 脚手架2、VSCode3.报错4.运行构建Vue3.0项目 1.使用Vite构建vue项目的方法以及步骤 1. 安装vite n…...

【2023】华为OD机试真题Java-题目0215-优雅数组
优雅数组 题目描述 如果一个数组中出现次数最多的元素出现大于等于 k k k 次,被称为k-优雅数组, k k k 也可以被称为优雅阈值。 例如,数组[1, 2, 3, 1, 2, 3, 1],它是一个3-优雅数组,因为元素1出现次数大于等于3次...

通过Prowork每日自动提醒待处理工作任务
对于中小团队来说,由于不需要繁琐的流程和高频的异地沟通,需要一款更适合中小团队的日程和项目管理工具。而Prowork就是这样一款敏捷高效的协同平台。Prowork与以往各种项目管理⼯具最⼤的不同在于,其弱化流程和弱化权限的特性,不…...

Linux自定义系统服务
文章目录一. Linux系统服务二. 自定义系统服务一. Linux系统服务 Linux 系统服务有时也称为守护程序,是在Linux启动时自动加载并在Linux退出时自动停止的系统任务,CentOS 7.x开始,CentOS开始使用 systemd服务来代替 daemon ,原来…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...
