BZOJ4403 序列统计
题目描述
给定三个正整数N、L和R,统计长度在1到N之间,元素大小都在L到R之间的单调不降序列的数量。输出答案对106+310^6+3106+3取模的结果。
输入
输入第一行包含一个整数T,表示数据组数。
第2到第T+1行每行包含三个整数N、L和R,N、L和R的意义如题所述。
1≤N,L,R≤10^9,1≤T≤100,输入数据保证L≤R。
输出
输出包含T行,每行有一个数字,表示你所求出的答案对106+310^6+3106+3取模的结果。
样例输入
2
1 4 5
2 4 5
样例输出
2
5
题解
前置知识:lucas定理
在区间[l,r][l,r][l,r]中长度为nnn的单调不降序列的数量,即Cr−l+1+n−1n=Cr−l+nnC_{r-l+1+n-1}^n=C_{r-l+n}^nCr−l+1+n−1n=Cr−l+nn个。
题意即求∑i=1nCr−l+ii\sum\limits_{i=1}^nC_{r-l+i}^ii=1∑nCr−l+ii。因为Cnm=Cnn−mC_n^m=C_n^{n-m}Cnm=Cnn−m,所以
∑i=1nCr−l+ii=∑i=1nCr−l+ir−l\sum\limits_{i=1}^nC_{r-l+i}^i=\sum\limits_{i=1}^nC_{r-l+i}^{r-l}i=1∑nCr−l+ii=i=1∑nCr−l+ir−l
又因为
∑i=mnCim=Cn+1m+1\sum\limits_{i=m}^nC_i^m=C_{n+1}^{m+1}i=m∑nCim=Cn+1m+1
所以
∑i=1nCr−l+ir−l=(∑i=0nCr−l+ir−l)−1=Cr−l+n+1r−l+1−1=Cr−l+n+1n−1\sum\limits_{i=1}^nC_{r-l+i}^{r-l}=(\sum\limits_{i=0}^nC_{r-l+i}^{r-l})-1=C_{r-l+n+1}^{r-l+1}-1=C_{r-l+n+1}^n-1i=1∑nCr−l+ir−l=(i=0∑nCr−l+ir−l)−1=Cr−l+n+1r−l+1−1=Cr−l+n+1n−1
Cr−l+n+1n−1C_{r-l+n+1}^n-1Cr−l+n+1n−1即为答案,用lucas定理求出即可。
code
#include<bits/stdc++.h>
using namespace std;
int n;
long long vt=1,x,y,ans=0,a[15],b[15];
void exgcd(long long c,long long d){if(d==0){x=1;y=0;return;}exgcd(d,c%d);long long t=x;x=y;y=t-c/d*y;
}
int main()
{scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%lld%lld",&a[i],&b[i]);vt=vt*a[i];}for(int i=1;i<=n;i++){exgcd(vt/a[i],a[i]);x=(x%a[i]+a[i])%a[i];ans=(ans+vt/a[i]*b[i]*x%vt)%vt;}printf("%lld",ans);return 0;
}
相关文章:

BZOJ4403 序列统计
题目描述 给定三个正整数N、L和R,统计长度在1到N之间,元素大小都在L到R之间的单调不降序列的数量。输出答案对106310^631063取模的结果。 输入 输入第一行包含一个整数T,表示数据组数。 第2到第T1行每行包含三个整数N、L和R,N、…...
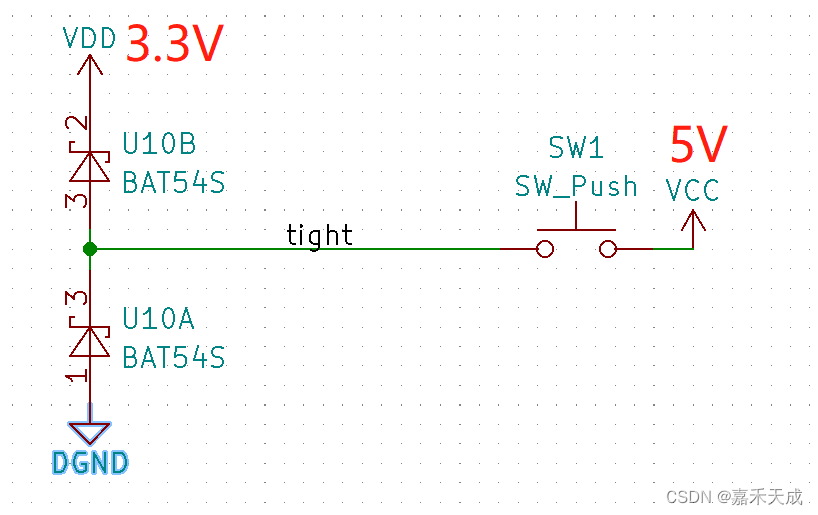
如何正确使用 钳位二极管
在电路设计中,经常遇到需要IO保护的场景,比如ADC采样,GPIO接收电平信号等。 常见的保护方法有分压,限幅,限流等。本次我们讨论限幅方法中的 钳位二极管。 我们以BAT54S为例,它的符号是这样的, 而在很多手册里,我们可以看到,一般是这样使用的: 因此,我设计了简化…...
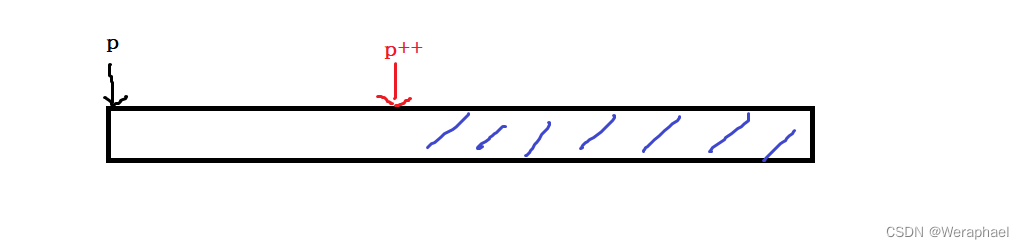
【C语言进阶】动态内存管理
👦个人主页:Weraphael ✍🏻作者简介:目前是C语言学习者 ✈️专栏:C语言航路 🐋 希望大家多多支持,咱一起进步!😁 如果文章对你有帮助的话 欢迎 评论💬 点赞&a…...

第一批因ChatGPT坐牢的人,已经上路了
大家好,我是 Jack。 ChatGPT 的火爆有目共睹,有人靠着它赚了第一桶金,也有人靠着它即将吃上第一顿牢饭。 任何一件东西的火爆,总会给一些聪明人带来机会。 艾尔登法环火的时候,一堆淘宝卖魂的;羊了个羊火…...

Eclipse下Maven的集成
Eclipse下Maven的集成 2.1指定本地maven环境 参考:Eclipse的Maven创建_叶书文的博客-CSDN博客_eclipse创建maven项目 指定用本地maven指定maven仓库设置和地址2.2创建maven项目 1.新建 2.目录设置 3.坐标设置(随便写就行) 4.目录结构 2.3配置…...

Elasticsearch7学习笔记(尚硅谷)
文章目录一、ElasticSearch概述1、ElasticSearch是什么2、全文搜索引擎3、ElasticSearch 和 Solr3.1 概述3.2 比较总结二、Elasticsearch入门1、Elasticsearch安装1.1 下载使用1.2 数据格式2、索引操作3、文档操作(了解)3.1 创建文档3.2 文档查询3.3 文档…...

前端学习第一阶段-第7章 品优购电商项目
7-1 品优购项目介绍及准备工作 01-品优购项目导读 02-网站制作流程 03-品优购项目规划 04-品优购项目搭建 05-品优购项目-样式的模块化开发 06-品优购项目-favicon图标制作 07-品优购项目-TDK三大标签SEO优化 7-2 首页Header区域实现 08-品优购首页-快捷导航shortcut结构搭建 0…...

cocos2dx 4.0 - cpp - pc版 环境搭建
开发环境vs2022 cocos2dx4.0 python2.7.18 cmake3.25安装教程(环境搭建)安装VS2022-Community, 勾选c进行安装安装cmake3.25, 勾选环境变量进行安装安装python2.7.18, 勾选环境变量进行安装下载cocos2dx4.0并解压配置cocos2dx:运行cmd,进入…...
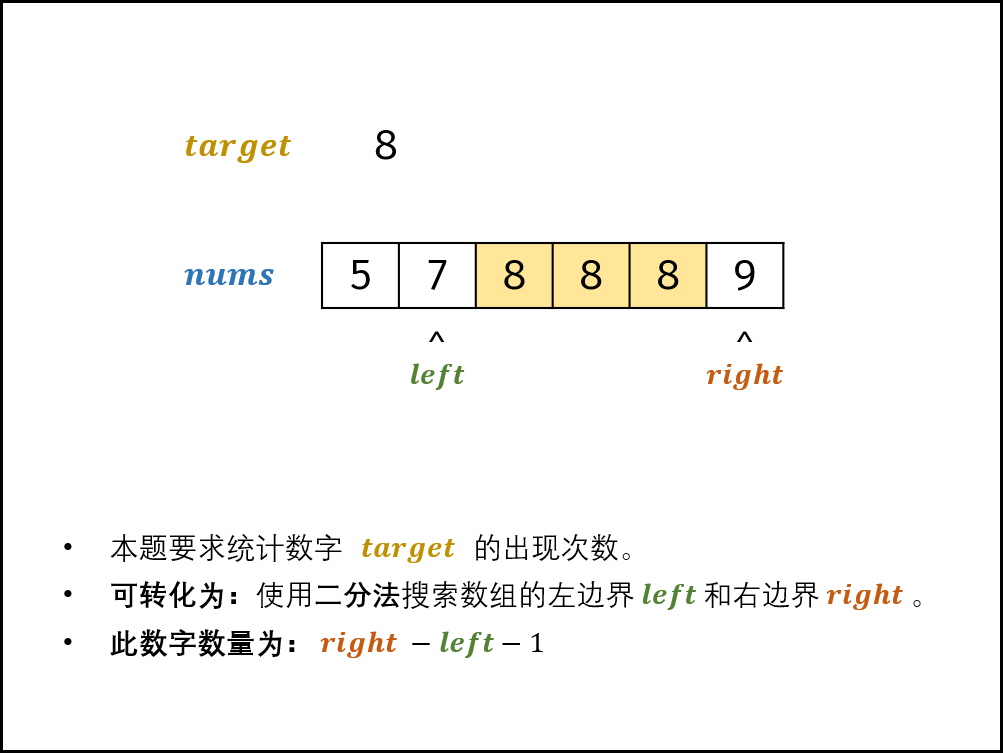
剑指 Offer 53 - I. 在排序数组中查找数字 I
原题链接 难度:easy\color{Green}{easy}easy 题目描述 统计一个数字在排序数组中出现的次数。 示例 1: 输入: nums [5,7,7,8,8,10], target 8 输出: 2示例 2: 输入: nums [5,7,7,8,8,10], target 6 输出: 0提示: 0<nums.length<1050 <…...
 | 机试题算法思路 【2023】)
华为OD机试 - 删除指定目录(Python) | 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 热点网络统计 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 查找单入口空闲区域 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 好朋友 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 找出同班小朋友 | 备考思路,刷题要点…...

PowerShell Install Office 2021 Pro Plus Viso Professional
前言 微软Office在很长一段时间内都是最常用和最受欢迎的软件。从小型创业公司到大公司,它的使用比例相当。它可以很容易地从微软的官方网站下载。但是,微软只提供安装程序,而不提供完整的软件供下载。这些安装文件通常比较小。下载并运行后,安装的文件将从后端服务器安装M…...

KubeSphere实战
文章目录一、KubeSphere平台安装1、Kubernetes上安装KubeSphere1.1 安装docker1.2 安装Kubernetes1.3 前置环境之nfs存储1.4 前置环境之metrics-server1.5 安装KubeSphere2、Linux单节点部署KubeSphere3、Linux多节点部署KubeSphere(推荐)二、KubeSphere实战1、多租户实战2、中…...

Linux 简介
Linux 内核最初只是由芬兰人林纳斯托瓦兹(Linus Torvalds)在赫尔辛基大学上学时出于个人爱好而编写的。 Linux 是一套免费使用和自由传播的类 Unix 操作系统,是一个基于 POSIX 和 UNIX 的多用户、多任务、支持多线程和多 CPU 的操作系统。 …...
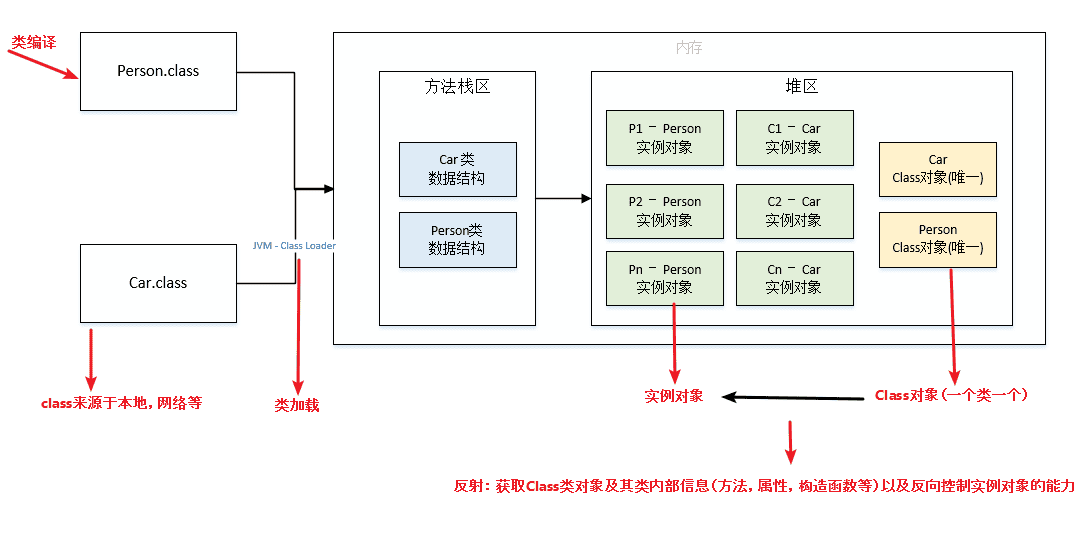
java面试题-泛型异常反射
泛型1.什么是泛型?Java是一种强类型语言,数据类型在编译时必须确定。如果我们想要在代码中使用不同类型的数据,那么就需要为每种类型分别写出相应的代码。这样会导致代码冗长、重复,也不便于维护。为了解决这个问题,Ja…...

详细解读ChatGPT:如何调用ChatGPT的API接口到官方例子的说明以及GitHub上的源码应用和csdn集成的ChatGPT
文章目录1. 解读ChatGPT1.1 词语解释1.2 功能解读2. GitHub上ChatGPT的应用源码3. 调用ChatGPT的API4. 官方例子说明5. 集成ChatGPT自ChatGPT出来到如今,始终走在火热的道路上,如今日活用户破亿,他为何有如此大的魅力,深受广大用户…...

九龙证券|最新评级情况出炉,机构扎堆这一板块!聚氨酯龙头获得最多关注
本周算计254家上市公司获组织“买入型”评级。 电子板块评级组织扎堆 证券时报数据宝计算,2月13日至17日,A股市场53家组织算计进行347次评级,254家上市公司获“买入型”评级(包含买入、增持、强烈推荐、推荐)。 从申…...
考研复试机试 | C++ | 尽量不要用python,很多学校不支持
目录1.1打印日期 (清华大学上机题)题目:代码:1.2改一改:上一题反过来问题代码:2.Day of Week (上交&&清华机试题)题目:代码:3.剩下的树(清…...

ChatGPT时代,别再折腾孩子了
今天这篇完全是从两件事儿有感而发。昨天在文印店,在复印机上看到装订好的几页纸,我瞥了一眼,是历史知识点:隋朝大运河分为四段,分别是___ ___ ___ ___,连接了五大河___ ___ ___ ___ ______ 年ÿ…...

万字干货 | 荔枝魔方基于云原生的架构设计与实践
近年来,荔枝集团在国内和海外的业务迅速发展,业务数据规模也是成几何式地增长,海量数据的计算分析场景、业务智能算法应用需求随之而生,为了快速地满足业务发展的需要,我们面临着诸多的技术挑战。技术挑战工程问题资源…...

#科研筑基# python初学自用笔记 第九篇 面向对象编程
面向对象编程 Object Oriented Programming ,简称OOP,是一种程序设计思想,这种思想把对象作为程序的基本单元。类是抽象的,对象是具体的,一种类包括其特定的数据或属性,以及操作数据的函数(方法…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...
