剑指 Offer 53 - I. 在排序数组中查找数字 I
原题链接
难度:easy\color{Green}{easy}easy
题目描述
统计一个数字在排序数组中出现的次数。
示例 1:
输入: nums = [5,7,7,8,8,10], target = 8
输出: 2
示例 2:
输入: nums = [5,7,7,8,8,10], target = 6
输出: 0
提示:
- 0<=nums.length<=1050 <= nums.length <= 10^{5}0<=nums.length<=105
- −109<=nums[i]<=109-10^{9} <= nums[i] <= 10^{9}−109<=nums[i]<=109
- numsnumsnums 是一个非递减数组
- −109<=target<=109-10^{9} <= target <= 10^{9}−109<=target<=109
注意:
-
本题与主站 34 题相同(仅返回值不同):https://leetcode-cn.com/problems/find-first-and-last-position-of-element-in-sorted-array/
-
面试官出这题的话肯定是想让你写二分的啦 其他没用。
-
给面试官说有两种类型的解法,一种是暴力,一种是二分法求边界,体现递进的思考过程,别上来一言不发写个二分,失去一个表现机会。
-
对于二分法,我们可以分别求左边界和右边界,也可以二分求左边界之后接着遍历计数,两种情况对应在真实场景下连续相等的数据一般有多长。如果经常出现很长一串连续相等的数据,就用二分法求右边界,否则容易使算法退化到
O(n)。 -
分析完了之后,给一个规范的解法,注意函数驼峰式命名这些能体现你专业性的小细节
算法1
(模拟)
创建一个变量 ans,扫描整个数组,如果数组中的值等于 target,那么 ans 就加一,最后输出答案。
复杂度分析
-
时间复杂度:O(n)O(n)O(n),其中 nnn 是数组的长度。需要遍历数组一次。
-
空间复杂度 : O(1)O(1)O(1),只需要常数空间存放若干变量。
C++ 代码
class Solution {
public:int search(vector<int>& nums, int target) {int ans = 0;for (int i = 0; i < nums.size(); i ++) {if (nums[i] == target)ans ++;}return ans;}
};
算法2
(二分)
-
排序数组
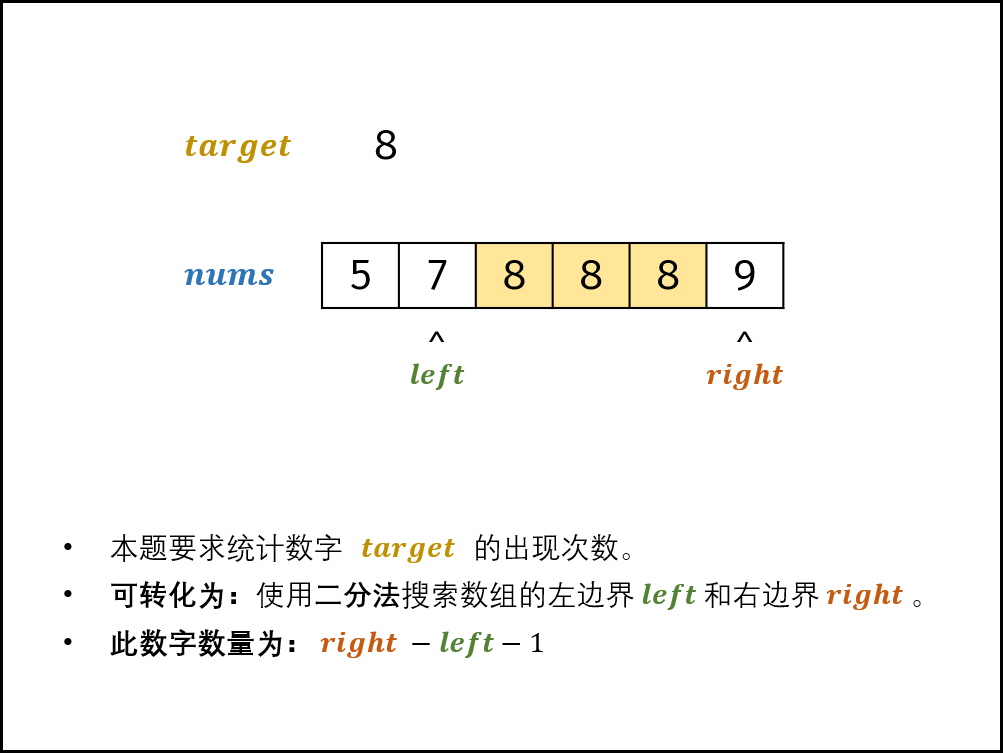
nums中的所有数字target形成一个窗口,记窗口的 左 / 右边界 索引分别为left和right,分别对应窗口左边 / 右边的首个元素。 -
本题要求统计数字
target的出现次数,可转化为:使用二分法分别找到 左边界left和 右边界right,易得数字target的数量为right−left−1。
复杂度分析
-
时间复杂度:O(logn)O(logn)O(logn),二分法为对数级别复杂度。
-
空间复杂度 : O(1)O(1)O(1),几个变量使用常数大小的额外空间。
C++ 代码
class Solution {
public:int search(vector<int>& nums, int target) {if (nums.size() == 0) return 0;int l = 0, r = nums.size() - 1;int ans = 0;//寻找最左边的下标while (l < r) {int mid = (l + r) / 2;if (nums[mid] >= target)r = mid;else l = mid + 1;}if (nums[l] != target) return ans;int left = l;l = 0, r = nums.size() - 1;//寻找右边的下标while (l < r) {int mid = (l + r + 1) / 2;if (nums[mid] <= target)l = mid;else r = mid - 1;}int right = l;ans = right - left + 1;return ans;}
};
相关文章:

剑指 Offer 53 - I. 在排序数组中查找数字 I
原题链接 难度:easy\color{Green}{easy}easy 题目描述 统计一个数字在排序数组中出现的次数。 示例 1: 输入: nums [5,7,7,8,8,10], target 8 输出: 2示例 2: 输入: nums [5,7,7,8,8,10], target 6 输出: 0提示: 0<nums.length<1050 <…...
 | 机试题算法思路 【2023】)
华为OD机试 - 删除指定目录(Python) | 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 热点网络统计 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 查找单入口空闲区域 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 好朋友 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 找出同班小朋友 | 备考思路,刷题要点…...

PowerShell Install Office 2021 Pro Plus Viso Professional
前言 微软Office在很长一段时间内都是最常用和最受欢迎的软件。从小型创业公司到大公司,它的使用比例相当。它可以很容易地从微软的官方网站下载。但是,微软只提供安装程序,而不提供完整的软件供下载。这些安装文件通常比较小。下载并运行后,安装的文件将从后端服务器安装M…...

KubeSphere实战
文章目录一、KubeSphere平台安装1、Kubernetes上安装KubeSphere1.1 安装docker1.2 安装Kubernetes1.3 前置环境之nfs存储1.4 前置环境之metrics-server1.5 安装KubeSphere2、Linux单节点部署KubeSphere3、Linux多节点部署KubeSphere(推荐)二、KubeSphere实战1、多租户实战2、中…...

Linux 简介
Linux 内核最初只是由芬兰人林纳斯托瓦兹(Linus Torvalds)在赫尔辛基大学上学时出于个人爱好而编写的。 Linux 是一套免费使用和自由传播的类 Unix 操作系统,是一个基于 POSIX 和 UNIX 的多用户、多任务、支持多线程和多 CPU 的操作系统。 …...
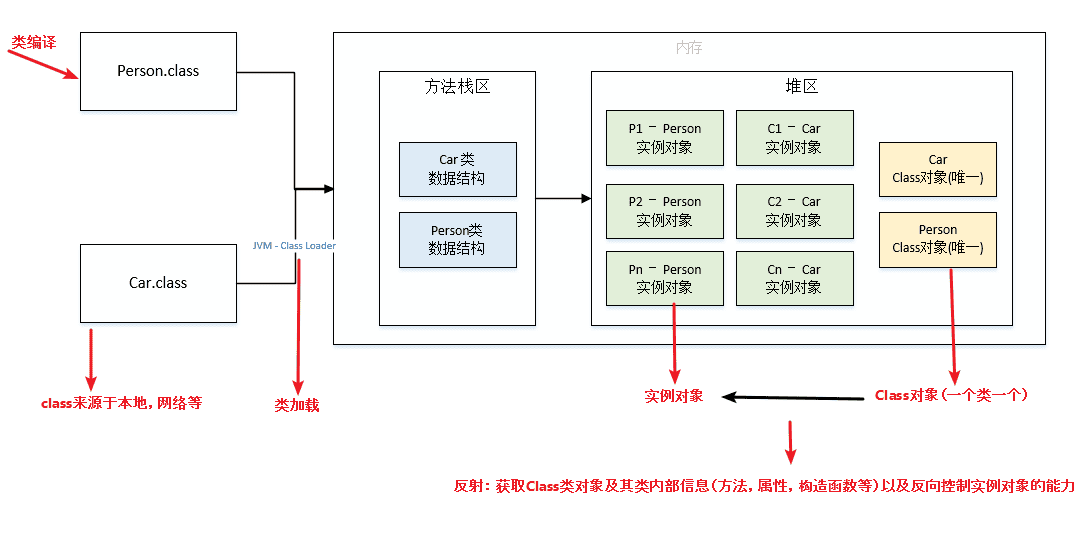
java面试题-泛型异常反射
泛型1.什么是泛型?Java是一种强类型语言,数据类型在编译时必须确定。如果我们想要在代码中使用不同类型的数据,那么就需要为每种类型分别写出相应的代码。这样会导致代码冗长、重复,也不便于维护。为了解决这个问题,Ja…...

详细解读ChatGPT:如何调用ChatGPT的API接口到官方例子的说明以及GitHub上的源码应用和csdn集成的ChatGPT
文章目录1. 解读ChatGPT1.1 词语解释1.2 功能解读2. GitHub上ChatGPT的应用源码3. 调用ChatGPT的API4. 官方例子说明5. 集成ChatGPT自ChatGPT出来到如今,始终走在火热的道路上,如今日活用户破亿,他为何有如此大的魅力,深受广大用户…...

九龙证券|最新评级情况出炉,机构扎堆这一板块!聚氨酯龙头获得最多关注
本周算计254家上市公司获组织“买入型”评级。 电子板块评级组织扎堆 证券时报数据宝计算,2月13日至17日,A股市场53家组织算计进行347次评级,254家上市公司获“买入型”评级(包含买入、增持、强烈推荐、推荐)。 从申…...
考研复试机试 | C++ | 尽量不要用python,很多学校不支持
目录1.1打印日期 (清华大学上机题)题目:代码:1.2改一改:上一题反过来问题代码:2.Day of Week (上交&&清华机试题)题目:代码:3.剩下的树(清…...

ChatGPT时代,别再折腾孩子了
今天这篇完全是从两件事儿有感而发。昨天在文印店,在复印机上看到装订好的几页纸,我瞥了一眼,是历史知识点:隋朝大运河分为四段,分别是___ ___ ___ ___,连接了五大河___ ___ ___ ___ ______ 年ÿ…...

万字干货 | 荔枝魔方基于云原生的架构设计与实践
近年来,荔枝集团在国内和海外的业务迅速发展,业务数据规模也是成几何式地增长,海量数据的计算分析场景、业务智能算法应用需求随之而生,为了快速地满足业务发展的需要,我们面临着诸多的技术挑战。技术挑战工程问题资源…...

#科研筑基# python初学自用笔记 第九篇 面向对象编程
面向对象编程 Object Oriented Programming ,简称OOP,是一种程序设计思想,这种思想把对象作为程序的基本单元。类是抽象的,对象是具体的,一种类包括其特定的数据或属性,以及操作数据的函数(方法…...

Python快速上手系列--邮件发送--详解篇
本章就来一起学习一下跑完自动化脚本后如何自动的发送邮件到指定的邮箱。zmail操作:1. 导包 import zmail2. 邮件内容,包含:主题(subject)、正文(content_text)、附件(attachments)3. 发件人信息,包含:发件人账号&…...
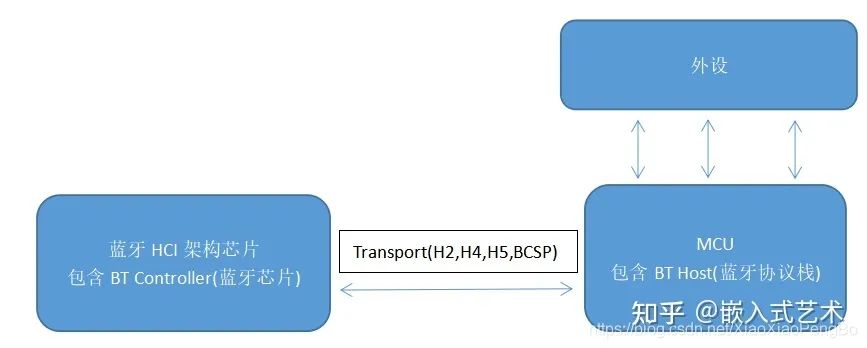
【Bluetooth开发】蓝牙开发入门
BLE 蓝牙设备在生活中无处不在,但是我们也只是将其作为蓝牙模块进行使用,发送简单的AT命令实现数据收发。 那么,像对于一些复杂的使用场合:“车载蓝牙”、"智能手表"、“蓝牙音箱”等,我们不得不去了解底层…...

07:进阶篇 - 在程序中嵌入 CTK Plugin Framework
作者: 一去、二三里 个人微信号: iwaleon 微信公众号: 高效程序员 如果已经创建了一个应用程序,现在要将 CTK Plugin Framework 嵌入其中,该如何进行呢? 下面,以《06:进阶篇 - Hello,CTK!》中的插件为例,来演示如何使用 CTK Plugin Framework 来加载插件并获取特定…...

快速低成本动画视频课
快速低成本动画视频课Character Animator能做什么如何用character animator制作动画视频Animate能做什么Adobe Animate和Character Animator结合,如何快速制作低成本动画视频课Character Animator能做什么 Character Animator是Adobe公司的一个动画制作软件&#x…...
)
大数据平台测试-软件测试常见面试回答(持续更新)
面试造航母,入职拧螺丝。面试,讲点面试官想听的。。。 1、你有过漏测的经历吗? 答:这道题肯定是回答有。然后展开描述。就类似面试官问 你印象比较深的一个bug。。。 测试无穷尽,质量也并非测试一个岗位的责任&…...

链表学习之反转链表
链表解题技巧 额外的数据结构(哈希表);快慢指针;虚拟头节点; 反转链表 分别实现单向链表和双向链表的反转。 要求:长度为N的链表,时间复杂度为O(N),额外空间复杂度为O(1)。 反转…...
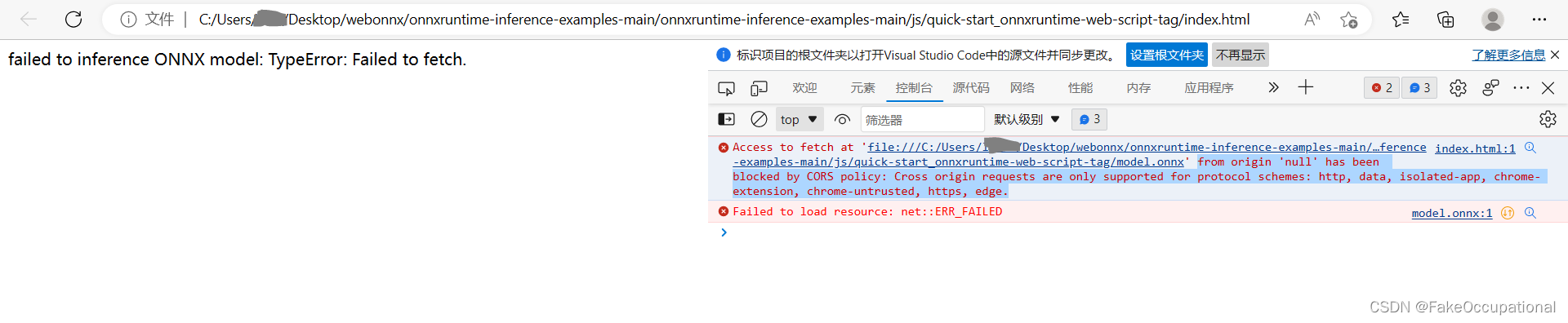
ONNXRUNTUIME实例分割网络说明
ONNXRUNTUIME c使用(分割网络)与相关资料(暂记) initiate a env with an id name(使用id名称启动env) create session (创建会话 ) onnxenv -> sessioninputname [“x”] ,outputname [“t”]inputnodedim [[1,1,192,192…...

几行代码,就写完懒加载啦?
Ⅰ、前言 「懒加载」是网页中非常 常见的;为了减少系统的压力,对于一些电商系统出场频率非常高;那么大家一般用什么方式去实现 「懒加载」 呢 ? ① 通过 scroll 的形式: 通过 滚动「scroll」事件,然后去判…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...
