链表学习之反转链表
链表解题技巧
- 额外的数据结构(哈希表);
- 快慢指针;
- 虚拟头节点;
反转链表
分别实现单向链表和双向链表的反转。
要求:长度为N的链表,时间复杂度为O(N),额外空间复杂度为O(1)。
反转单向链表:
方法1(使用栈,时:O(N),空:O(N)):
- 第一次遍历将数据添加至栈中;
- 定义一个空节点,tmp记录,cur指向该节点;
- 栈不为空开始循环出栈:
- cur的next指向的栈顶元素;
- 栈顶元素出栈;
- cur移动到next的位置;
- cur现在在最后一个位置,将其next赋值为nullptr;
- cur指向tmp(空节点)的next位置,并删除tmp;
- 返回cur(新的头节点);
LinkedNode* LinkedList::reverseWithStack(LinkedNode *head) {if (head == nullptr || head->next == nullptr) {return head;}std::stack<LinkedNode*> stk;LinkedNode* cur = head;while (cur) {stk.push(cur);cur = cur->next;}LinkedNode* tmp = new LinkedNode();cur = tmp;while (!stk.empty()) {cur->next = stk.top();stk.pop();cur = cur->next;}cur->next = nullptr;cur = tmp->next;delete tmp;return cur;
}
方法2(双指针,时:O(N),空:O(1)):
双指针解法:
- 定义两个指针new_head,cur,初始new_head指向head,cur指向head的next;
- cur不为nullptr则开始循环:
- head的next赋值为cur的next;
- cur的next赋值为new_head;
- new_head移动到cur;
- cur移动到head的next;
- 最后返回new_head即可。
LinkedNode* LinkedList::reverse(LinkedNode *head) {if (head == nullptr || head->next == nullptr) {return head;}LinkedNode *new_head = head;LinkedNode *cur = head->next;while (cur) {head->next = cur->next;cur->next = new_head;new_head = cur;cur = head->next;}return new_head;
}
反转双链表
DoubleLinkedNode* LinkedList::reverseDoubleLinkedList(DoubleLinkedNode *head) {if (head == nullptr || head->next == nullptr) {return head;}DoubleLinkedNode *pre = head;DoubleLinkedNode *cur = head->next;while (cur) {DoubleLinkedNode *tmp = pre->next;pre->next = pre->pre;pre->pre = tmp;pre = cur;cur = cur->next;}return pre;
}
相关文章:

链表学习之反转链表
链表解题技巧 额外的数据结构(哈希表);快慢指针;虚拟头节点; 反转链表 分别实现单向链表和双向链表的反转。 要求:长度为N的链表,时间复杂度为O(N),额外空间复杂度为O(1)。 反转…...
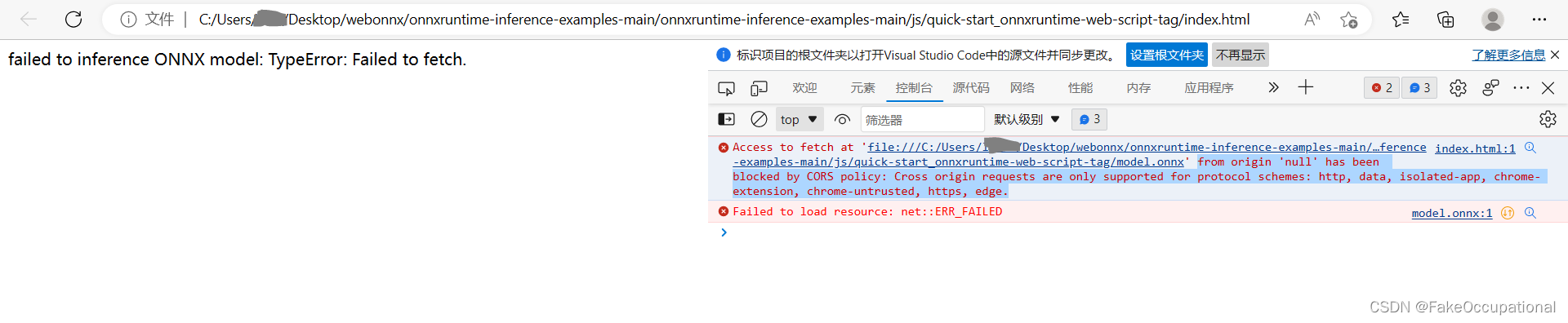
ONNXRUNTUIME实例分割网络说明
ONNXRUNTUIME c使用(分割网络)与相关资料(暂记) initiate a env with an id name(使用id名称启动env) create session (创建会话 ) onnxenv -> sessioninputname [“x”] ,outputname [“t”]inputnodedim [[1,1,192,192…...

几行代码,就写完懒加载啦?
Ⅰ、前言 「懒加载」是网页中非常 常见的;为了减少系统的压力,对于一些电商系统出场频率非常高;那么大家一般用什么方式去实现 「懒加载」 呢 ? ① 通过 scroll 的形式: 通过 滚动「scroll」事件,然后去判…...
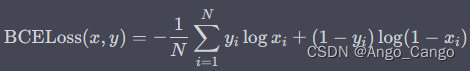
PyTorch常用的损失函数(ChatGPT)
L1Loss nn.L1Loss 也称为平均绝对误差(Mean Absolute Error,MAE)。它计算预测值与真实值之间的差异(即误差),然后取绝对值并求和,最后除以样本数量得到平均误差。具体来说,对于一批…...

LeetCode——1237. 找出给定方程的正整数解
一、题目 来源:力扣(LeetCode) 链接:https://leetcode.cn/problems/find-positive-integer-solution-for-a-given-equation/description/ 翻译一下题目 意思是,这是一个二维单调递增的函数,函数一共有 9 …...

系统编程中的进程的概念No.3【进程状态】
引言: 北京时间:2023/2/17/8:17,目前听着超能陆战队主题曲《Immortals》,感觉又要螺旋式升天,并且为我今天上午没课感到happy,所以继我们很久以前的关于进程的博客,今天我们就再来学习一下有关…...

推荐 3 款 Golang 语义化版本库
文章目录1.什么是语义化版本 2.0.02.Golang 语义化版本库比较3.小结参考文献1.什么是语义化版本 2.0.0 语义化版本 2.0.0(Semantic Versioning 2.0.0)是一种用于标识软件版本的约定和规范。它包含三个数字组成的版本号,格式为“MAJOR.MINOR.…...
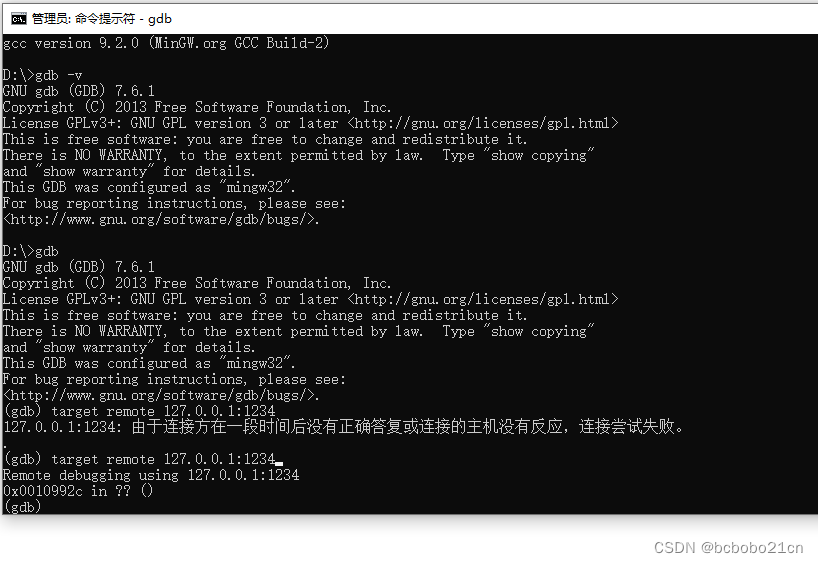
Windows平台使用gdb连接qemu虚拟机上的系统
先安装MinGW; 除了gcc、g,把gdb也选上;可能选第一个就可以了,不清楚把后面几个也选上; 安装完成看一下gcc, g,gdb,编译工具和调试器都有了; 把bin目录加到环境变量; 看一…...
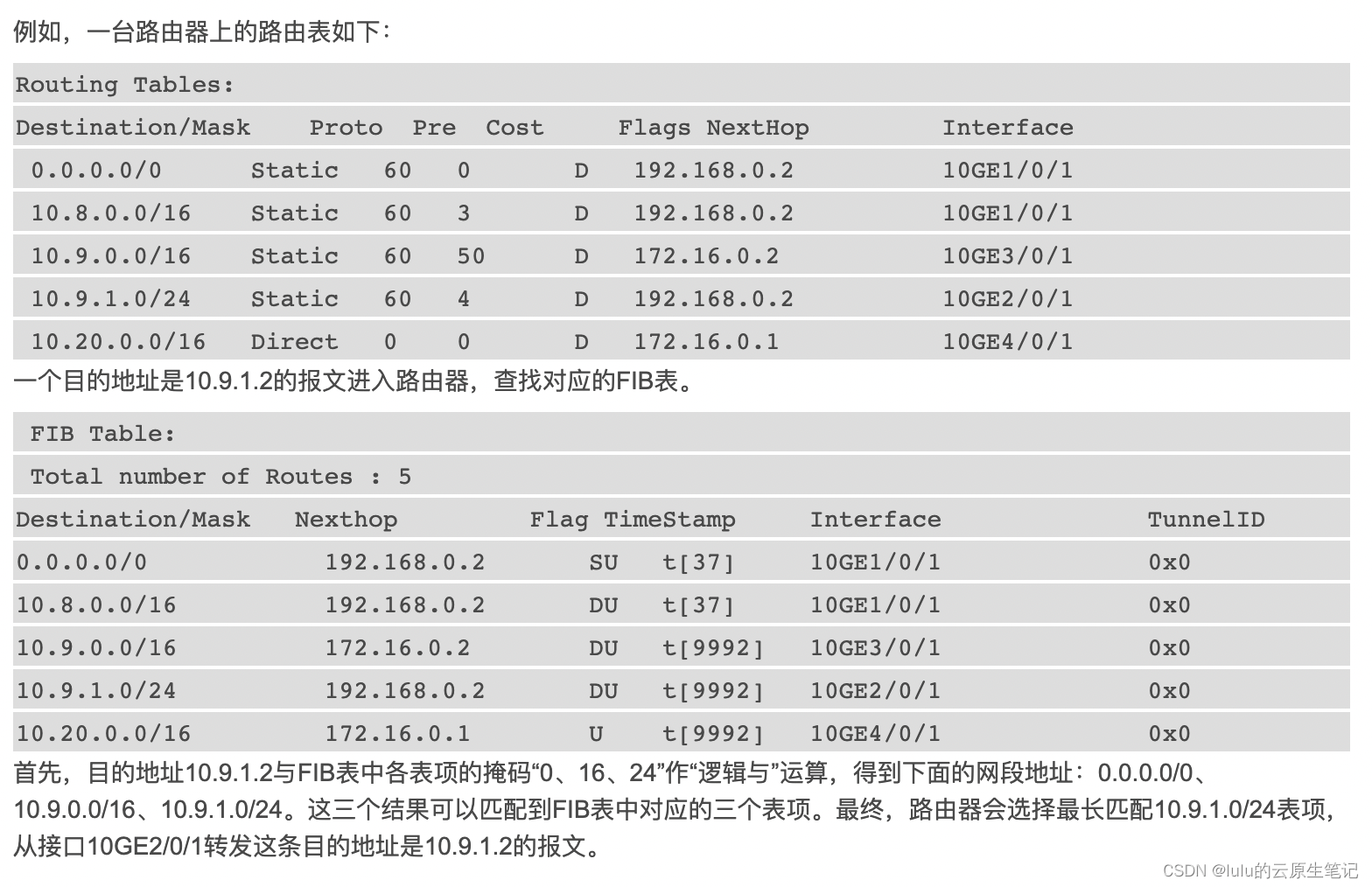
【博客624】MAC地址表、ARP表、路由表(RIB表)、转发表(FIB表)
MAC地址表、ARP表、路由表(RIB表/FIB表) MAC地址表 MAC地址表是交换机等网络设备记录MAC地址和端口的映射关系,代表了交换机从哪个端口学习到了某个MAC地址,交换机把这个信息记录下来,后续交换机需要转发数据的时候就可以根据报文的目的MAC地…...

【蓝桥日记⑤】2014第五届省赛(软件类)JavaA组❆答案解析
【蓝桥日记⑤】2014第五届省赛(软件类)JavaA组☃答案解析 文章目录【蓝桥日记⑤】2014第五届省赛(软件类)JavaA组☃答案解析1、猜年龄2、李白打酒3、神奇算式4、写日志5、锦标赛6、六角填数7、绳圈8、兰顿蚂蚁9、斐波那契10、波动…...

Leetcode.1139 最大的以 1 为边界的正方形
题目链接 Leetcode.1139 最大的以 1 为边界的正方形 Rating : 1744 题目描述 给你一个由若干 0 和 1 组成的二维网格 grid,请你找出边界全部由 1 组成的最大 正方形 子网格,并返回该子网格中的元素数量。 如果不存在,则返回 0。…...

Bing+ChatGPT 对传统搜索引擎的降维打击
早些时候申请了新版 Bing 的内测资格,终于收到了通过的邮件。 一天的体验之后,我的感受是:当新版 Bing 具备了 ChatGPT 的聊天能力之后,它的能力不论是对传统搜索引擎,还是 ChatGPT 自身,都将是降维打击。 …...
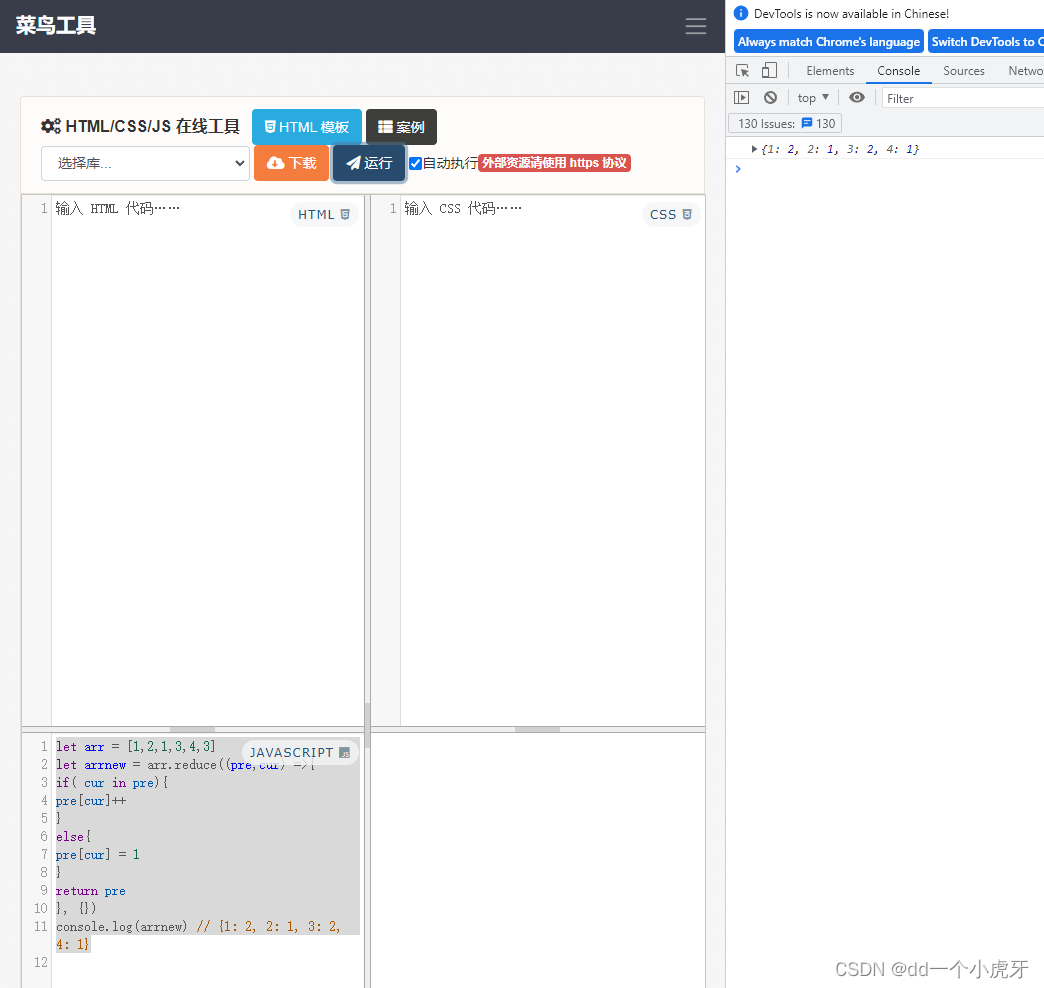
【JS】数组常用方法总结-功能、参数、返回值
数组常用方法总结-功能、参数、返回值 用简单的js示例 运行在线工具:链接: 菜鸟工具 菜鸟工具示意图: pu…...

pytest 单元测试前后置处理
文章目录方法1 setup/teardown方法2 fixture 夹具方法3 conftest.py测试用例执行前后的一些处理动作,也叫夹具。以下介绍使用前后置操作的几种方法。方法1 setup/teardown setup,每个测试用例执行前要进行的处理。 teardown,每个测试用例执行…...
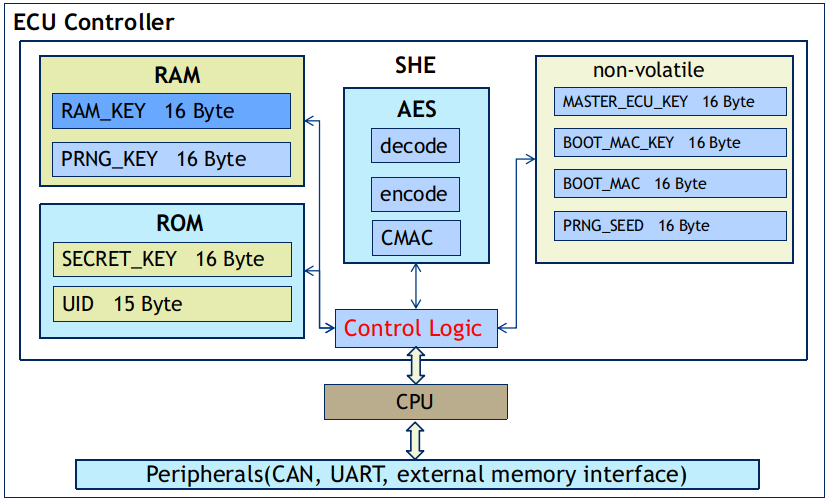
汽车安全硬件扩展 AUTOSAR SHE SecureHardwareExtensions
SHE(Secure Hardware Extension)在车联网中,被应用在车端ECU中负责安全存储与安全计算。是由HIS(由Audi、BMW、Porsche、Volkswagen组成)制定的标准,中文意思“安全硬件扩展”,是对任何给定微控…...
2023年美国大学生数学建模C题:预测Wordle结果建模详解+模型代码
目录 前言 一、题目理解 背景 解析 字段含义: 建模要求 二、建模思路 灰色预测: 编辑 二次指数平滑法: person相关性 只希望各位以后遇到建模比赛可以艾特认识一下我,我可以提供免费的思路和部分源码,以后…...

5、HAL库驱动W25Qxx
一、 SPI通信驱动W25Qxx 1、使用驱动文件快速配置工程代码驱动W25Qxx (此驱动文件只适合W25Qxx 16M及以下型号,因为访问地址位数不同) 注:本次使用SPI的方式进行访问W25Qxx Flash进行数据读写,关于W25Qxx芯片不会做…...
)
git rebase 洐合(变基)
洐合 把一个分支整合到另一个分支的办法有两种:merge(合并) 和 rebase(衍合) 为什么使用? 使提交记录更简洁 三种情况 第一种: 合并多条commit记录 git rebase -i HEAD~合并数量 HEAD~3&a…...

Kubernetes 1.18学习笔记
文章目录一、Kubernetes 概述和架构1、kubernetes 基本介绍2、Kubernetes 功能3、Kubernetes 架构组件4、Kubernetes 核心概念5、Kubernetes 工作原理二、Kubernetes 集群搭建1、系统环境准备1.1 安装要求1.2 系统初始化2、客户端工具kubeadm搭建2.1 安装步骤2.2 安装组件2.3 集…...

AJAX技术
AJAX技术 浏览器是多进程的,简单的说就是,浏览器每打开一个标签页,就相当于创建了一个独立的浏览器进程。但是js是基于单线程的,而这个线程就是浏览器的js引擎,浏览器无论在什么时候都只且只有一个线程在运行JavaScri…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...
