奶牛排队 java 思维题
👨🏫 5133. 奶牛排队
题目描述
约翰的农场有 n n n 头奶牛,每一头奶牛都有一个正整数编号。
不同奶牛的编号不同。
现在,这 n n n 头牛按某种顺序排成一队,每头牛都拿出一张纸条写下了其前方相邻牛的编号以及其后方相邻牛的编号。
注意:
- 这些奶牛并没有记下自己的编号。
- 位于队首的奶牛前方没有牛,所以它在前方相邻牛处写下的是数字 0 0 0。
- 位于队尾的奶牛后方没有牛,所有它在后方相邻牛处写下的是数字 0 0 0。
将所有奶牛写下的纸条收集起来并打乱顺序后交给你。
你的任务是根据这些纸条信息,推导出完整的奶牛队列。
输入格式
第一行包含整数 n n n,表示奶牛数量。
接下来 n n n 行,每行包含两个整数 a _ i , b _ i a\_i,b\_i a_i,b_i,表示其中一头奶牛写下的其前方相邻牛的编号以及其后方相邻牛的编号。
注意, a _ i a\_i a_i 或 b _ i b\_i b_i 可能为 0 0 0,这表示该奶牛没有前方相邻牛或后方相邻牛。
输出格式
输出共一行, n n n 个整数,按照从前到后的顺序输出队列中每头奶牛的编号。
数据范围
前 5 5 5 个测试点满足 2 ≤ n ≤ 5 2 \le n \le 5 2≤n≤5。
所有测试点满足 2 l e n ≤ 2 × 1 0 5 2 \\le n \le 2 \times 10^5 2len≤2×105, 0 ≤ a _ i , b _ i ≤ 1 0 6 0 \le a\_i,b\_i \le 10^6 0≤a_i,b_i≤106。
输入样例:
4
92 31
0 7
31 0
7 141
输出样例:
92 7 31 141
时间复杂度
O(n)
🍺 AC code
import java.util.Scanner;public class Main
{static int N = 1000010;static int[] a = new int[N];static int[] b = new int[N];static int[] mp = new int[N];static int[] cnt = new int[N];// 记录每个数出现的次数,出现在前面 +1,出现在后面 -1public static void main(String[] args){Scanner sc = new Scanner(System.in);int n = sc.nextInt();int idx = 0;// idx 记录当前牛在 a[i] 时 的下标 ifor (int i = 0; i < n; i++){a[i] = sc.nextInt();b[i] = sc.nextInt();cnt[a[i]]++;cnt[b[i]]--;mp[a[i]] = i;if (a[i] == 0)// 说明是第一头牛idx = i;}int val = 0;// val记录当前的值for (int i = 0; i < N; i++)if (cnt[i] == 1)val = i;//for (int i = 0; i < n; i++){System.out.print(val + " ");int nextVal = b[idx];// 当前牛的下标 idx 的 b(后一位)int nextIdx = mp[val];// 找到 (下一头牛的编号 == a[i]) 的 下标 ival = nextVal;idx = nextIdx;}}
}相关文章:

奶牛排队 java 思维题
👨🏫 5133. 奶牛排队 题目描述 约翰的农场有 n n n 头奶牛,每一头奶牛都有一个正整数编号。 不同奶牛的编号不同。 现在,这 n n n 头牛按某种顺序排成一队,每头牛都拿出一张纸条写下了其前方相邻牛的编号以及其…...

uniapp 微信小程序 判断数据返回的是jpg还是pdf,以及pdf预览
<template> <view class"approval-notice"><block v-for"(imgItem, idx) in drivingLicense" :key"idx">//如果是非图片,那就走pdf预览<view class"pdf-item" v-if"Object.keys(thumbnail).incl…...
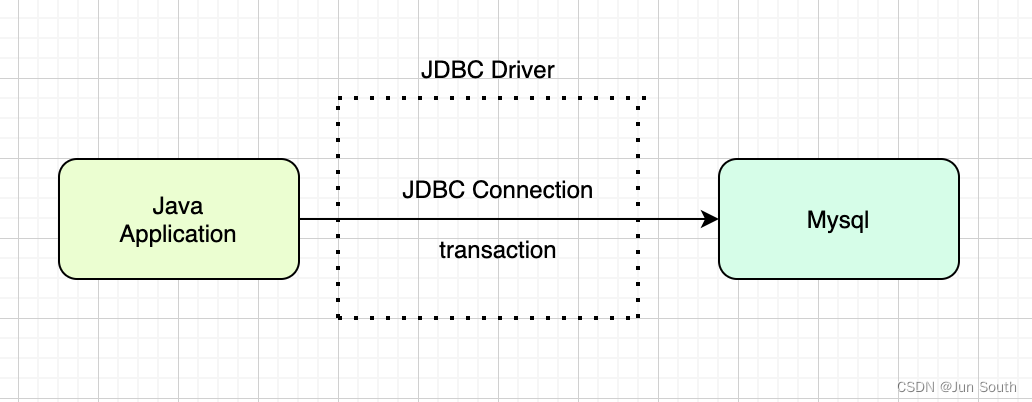
SpringBoot 的事务及使用
一、事务的常识 1、事务四特性(ACID) A 原子性:事务是最小单元,不可再分隔的一个整体。C 一致性:事务中的方法要么同时成功,要么都不成功,要不都失败。I 隔离性:多个事务操作数据库中同一个记录或多个记录时,对事务进…...

Android中的ABI
Android中的ABI ABI是Application Binary Interface的缩写。 ABI常表示两个程序模块之间的接口,且其中一个模块常为机器码级别的library或操作系统。 ABI定义了函数库的调用、应用的二进制文件(尤其是.so)如何运行在相应的系统平台上等细节…...

Python爬虫在用户行为模型构建中的应用与挑战
嗨,大家好!作为一名专业的爬虫代理,我今天要和大家分享一些关于爬虫与人类行为分析的知识。在数字化时代,我们每天都在互联网上留下大量的数据痕迹,通过分析这些数据,我们可以理解用户行为、性偏好和需求&a…...

LangChain与大模型的学习
这里写目录标题 问题记录1、库的版本问题 实例记录1、公司名生成2 提示模板的使用3LLM Chain 参考资料 问题记录 1、库的版本问题 openai.error.APIConnectionError: Error communicating with OpenAI: HTTPSConnectionPool(hostapi.openai.com, port443): Max retries excee…...

C语言标准定义的32个关键字
欢迎关注博主 Mindtechnist 或加入【智能科技社区】一起学习和分享Linux、C、C、Python、Matlab,机器人运动控制、多机器人协作,智能优化算法,滤波估计、多传感器信息融合,机器学习,人工智能等相关领域的知识和技术。 …...

PE半透明屏是怎么制造的?工艺、材料、应用
PE半透明屏是一种新型的屏幕材料,具有半透明的特点。 它由聚乙烯(PE)材料制成,具有良好的透明度和柔韧性。PE半透明屏广泛应用于建筑、广告、展览等领域,具有很高的市场潜力。 PE半透明屏的特点之一是其半透明性。 它…...

linux文本三剑客---grep,sed,awk
目录 grep 什么是grep? grep实例演示 命令参数: 案例演示: sed 概念: 常用选项: 案例演示: awk 概念: awk常用命令选项: awk变量: 内置变量 自定义变量 a…...
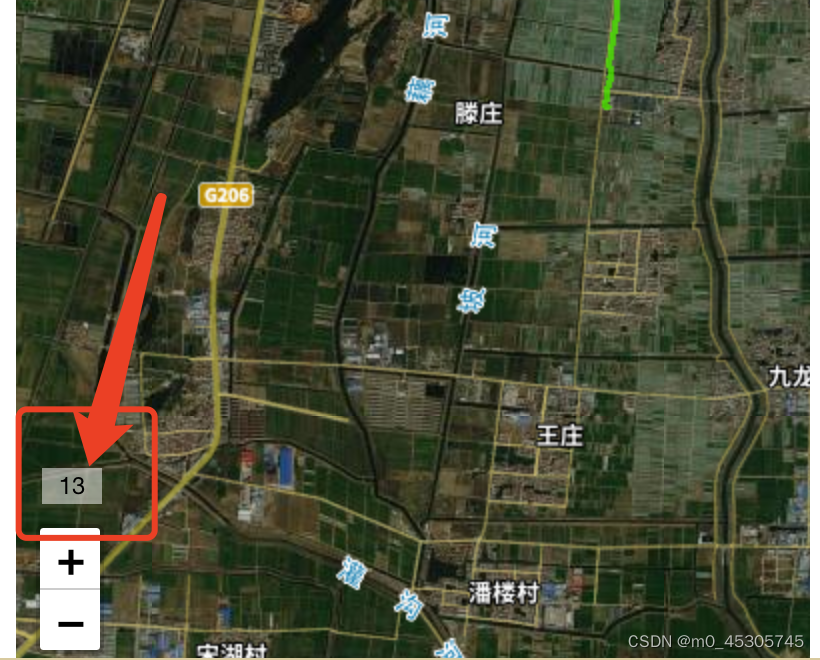
leaflet-uniapp 缩放地图的同时 显示当前缩放层级
记录实现过程: 需求为移动端用户在使用地图时,缩放地图的同时,可以获知地图此时缩放的级别。 效果图如下:此时缩放地图级别为13 map.on() 有对应的诸多行为 查看官网即可,这里根据需要为--zoomstart zoom zoomend 代…...
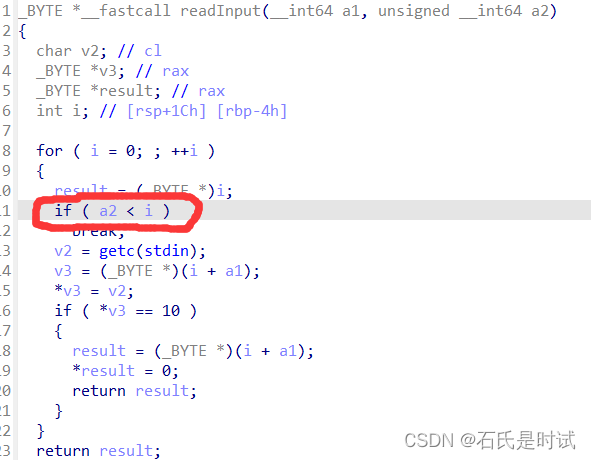
[Securinets CTF Quals 2023] Admin Service,ret2libc,One is enough
只作了3个pwn,第4个附件没下下来,第5个不会 Admin Service 这是个最简单的题,最后来弄出来。原来只是看过关于maps文件的,一直没什么印象。 题目一开始设置seccomp禁用execv等,看来是用ORW,然后建了个mm…...
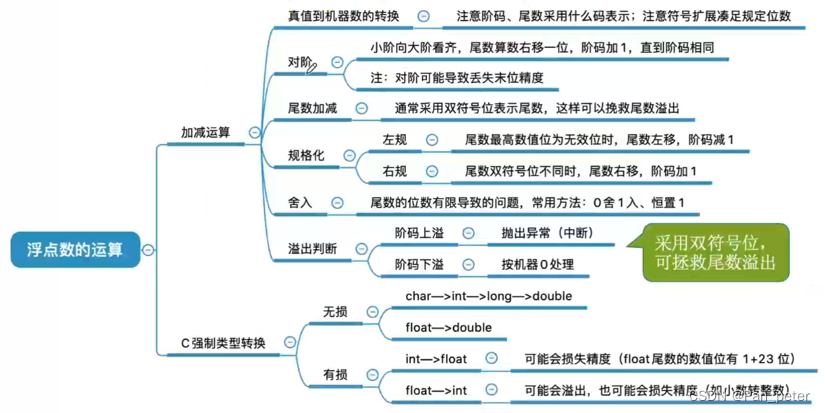
计算机组成原理-笔记-第二章
二、第二章——数据的表示和运算 1、进位制度(二进制、十进制) 2、BCD码(余三码、2421码) 编码方式 功能 好处 弊处 BCD码 将每个十进制数码转换为4位二进制码 精度高,适合直接用于数码管或LED等显示设备 编码…...

mysql大量数据导入记要
需求描述 在工作中经历过两个项目要对数据库中的数据做大量数据的导出,转换和导入的工作。对于不涉及数据格式转换的导出导入工作,一般都是数据的备份。这个工作一般都由DBA搞定。对于要进行格式转换的工作,一般还是要由程序员参与。除非DBA…...
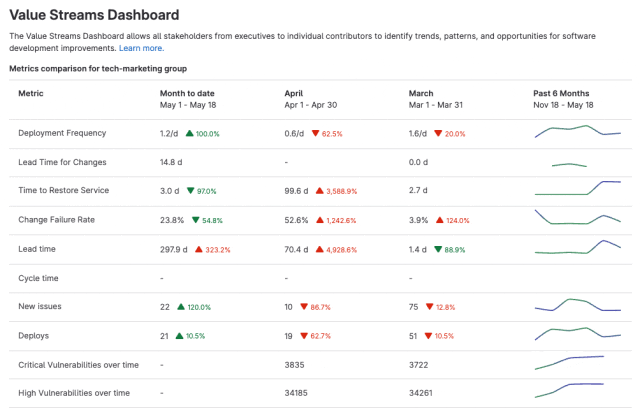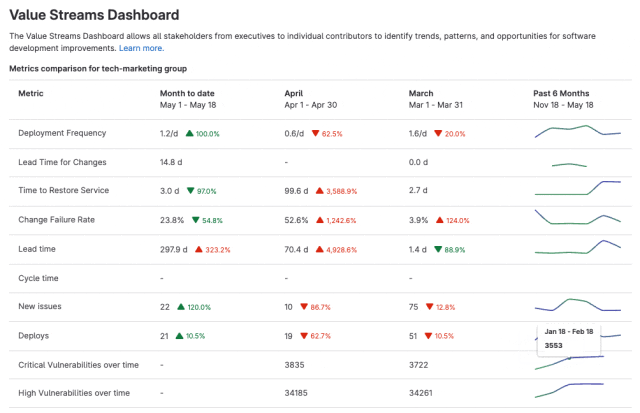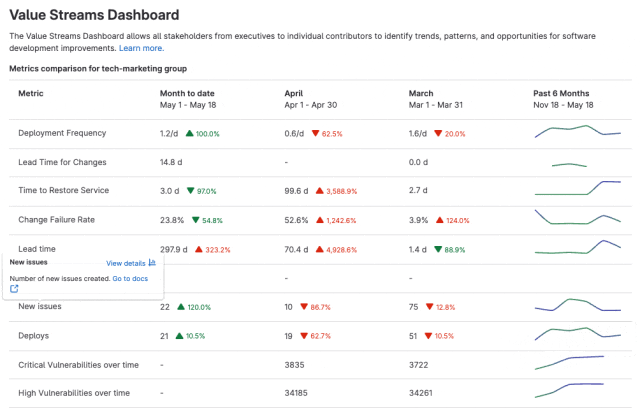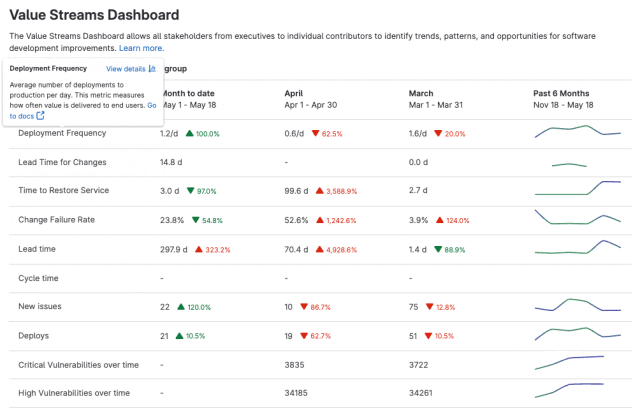
极狐GitLab 全新「价值流仪表盘」使用指南
本文来源:about.gitlab.com 作者:Haim Snir 译者:极狐(GitLab) 市场部内容团队 GitLab / 极狐GitLab 价值流仪表盘的使用相对简单,这种可以定制化的仪表盘能够让决策者识别数字化转型进程中的趋势及机遇。 如果你已经在用 GitLab…...

通过logrotate实现nginx容器内日志按天存储
场景 最近底层api需要上集群,于是用nginx做了转发,但是随着时间的增长,nginx的日志越来越大,磁盘空间也顶不住了,于是需要对日志进行分割,由于nginx原生是不支持日志按天存储和分割的,网上也介…...

广东珠海电子行业导入MES系统需要注意什么
一、电子行业工厂的生产特征 1.高度自动化: 电子行业的生产车间大多采用高度自动化的生产设备制造工艺。自动化流水线能够实现高效、精准和连续的生产过程,提升产品完整性和生产率。 2.多样化和个性化定制需求: 电子产品市场的需求多样化&…...

小红书2023/08/06Java后端笔试 AK
T1(模拟、哈希表) #include <bits/stdc.h>using namespace std;typedef long long LL; typedef pair<string, int> PSI;const int N 1e5 10;void solve() {string line, t;getline(cin, line);line ;vector<PSI> ans;unordered_m…...

3、有序数组的平方
有一个有序数组从大到小排列:-10 -5 1 2 3 4,将他们的每一项平方,然后再形成新的有序数组。 解法:双指针 因为前面是负数,后面是正数,平方和的最大值一定是从两端取得,所以可以定义一个头指针和…...
 的 MLOps)
用于自然语言处理 (NLP) 的 MLOps
介绍 自然语言处理( NLP )的人工智能关注的是计算机和人们如何用日常语言进行交流。鉴于 NLP 模型在生产系统中的部署,我们需要简化 NLP 应用程序的不断使用,从而使 MLOps(机器学习操作)对 NLP 有所帮助。在生产系统中自动创建、训练、测试和部署 NLP 模型是 MLOps for …...

C#抽象静态方法
抽象静态方法 在C# 11中,引入了对抽象静态接口成员的支持。这个特性可以让你在接口中定义静态抽象方法、属性、或事件。具体来说,一个接口可以定义一个或多个抽象静态成员,这些成员没有具体的实现。任何实现该接口的类或结构必须提供这些成员…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...

【iOS】 Block再学习
iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...

高效的后台管理系统——可进行二次开发
随着互联网技术的迅猛发展,企业的数字化管理变得愈加重要。后台管理系统作为数据存储与业务管理的核心,成为了现代企业不可或缺的一部分。今天我们要介绍的是一款名为 若依后台管理框架 的系统,它不仅支持跨平台应用,还能提供丰富…...

python基础语法Ⅰ
python基础语法Ⅰ 常量和表达式变量是什么变量的语法1.定义变量使用变量 变量的类型1.整数2.浮点数(小数)3.字符串4.布尔5.其他 动态类型特征注释注释是什么注释的语法1.行注释2.文档字符串 注释的规范 常量和表达式 我们可以把python当作一个计算器,来进行一些算术…...
