订单系统就该这么设计,稳的一批~
订单功能作为电商系统的核心功能,由于它同时涉及到前台商城和后台管理系统,它的设计可谓是非常重要的。就算不是电商系统中,只要是涉及到需要交易的项目,订单功能都具有很好的参考价值,说它是通用业务功能也不为过。今天就以mall项目中的订单功能为例,来聊聊订单功能的设计与实现。
mall项目简介
这里还是简单介绍下mall项目吧,mall项目是一套基于 SpringBoot + Vue + uni-app 的电商系统,目前在Github已有60K的Star,包括前台商城项目和后台管理系统,能支持完整的订单流程!涵盖商品、订单、购物车、权限、优惠券、会员等功能,功能很强大!
- 项目地址:https://github.com/macrozheng/mall
- 学习文档:https://www.macrozheng.com
功能设计
首先我们来看下mall项目中订单功能的设计,由于订单功能同时涉及到前台商城和后台管理系统,这里将分别讲解。
后台管理系统
后台管理系统的订单模块主要包括订单管理、订单设置、退货原因设置、退货申请设置功能。
订单管理
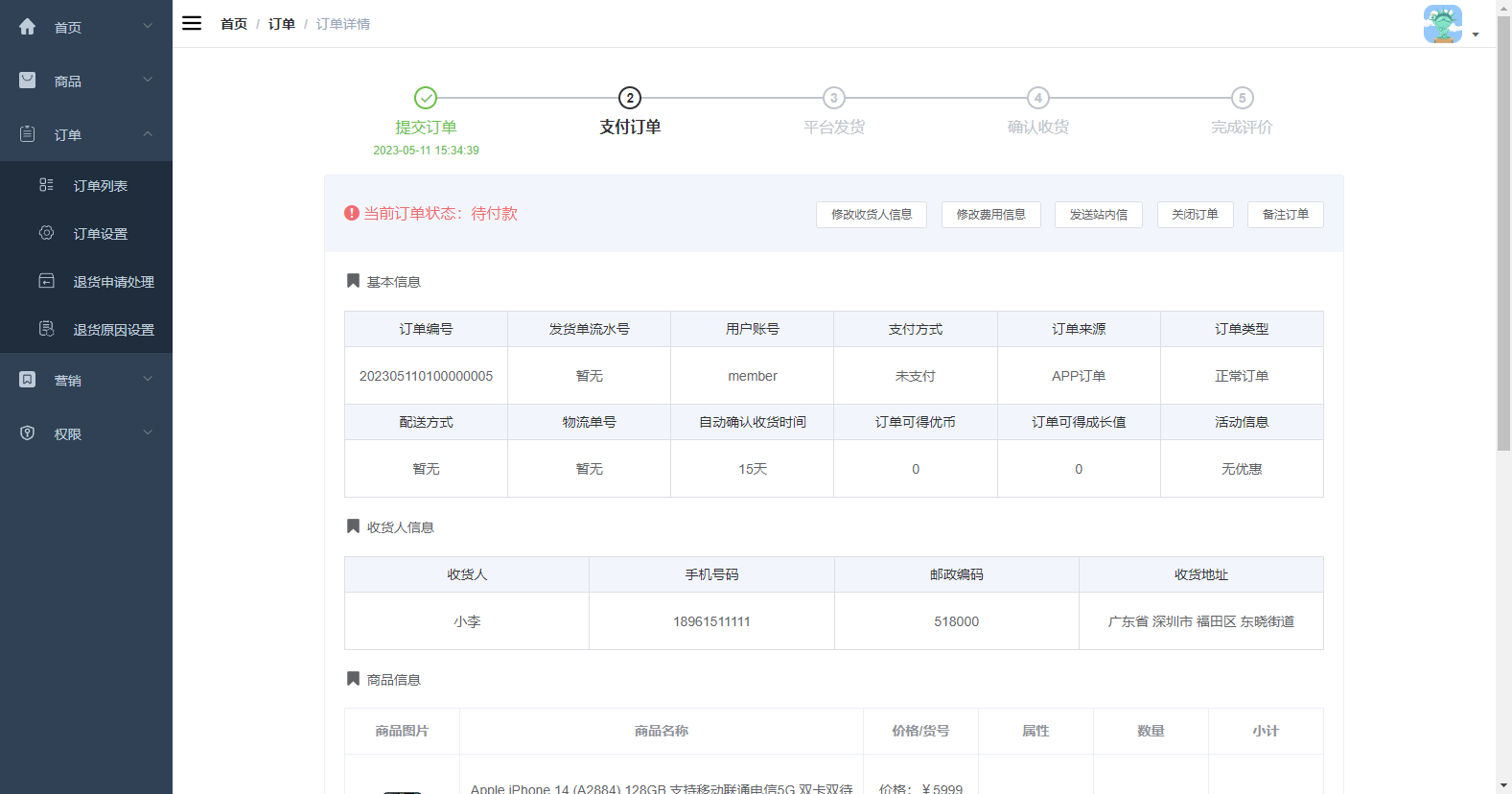
后台管理员在订单列表中可以实现查看订单、删除订单、订单发货、订单跟踪等操作。

针对不同状态下的订单,后台管理员在订单详情页还可以实现修改收货人信息、修改费用信息、关闭订单、备注订单等操作
订单设置
后台管理员可以对订单实现一些基础设置,例如订单超过多少时间自动关闭等等。

退货申请处理
后台管理员可以对退货申请进行处理,比如说确认退货或拒绝退货。

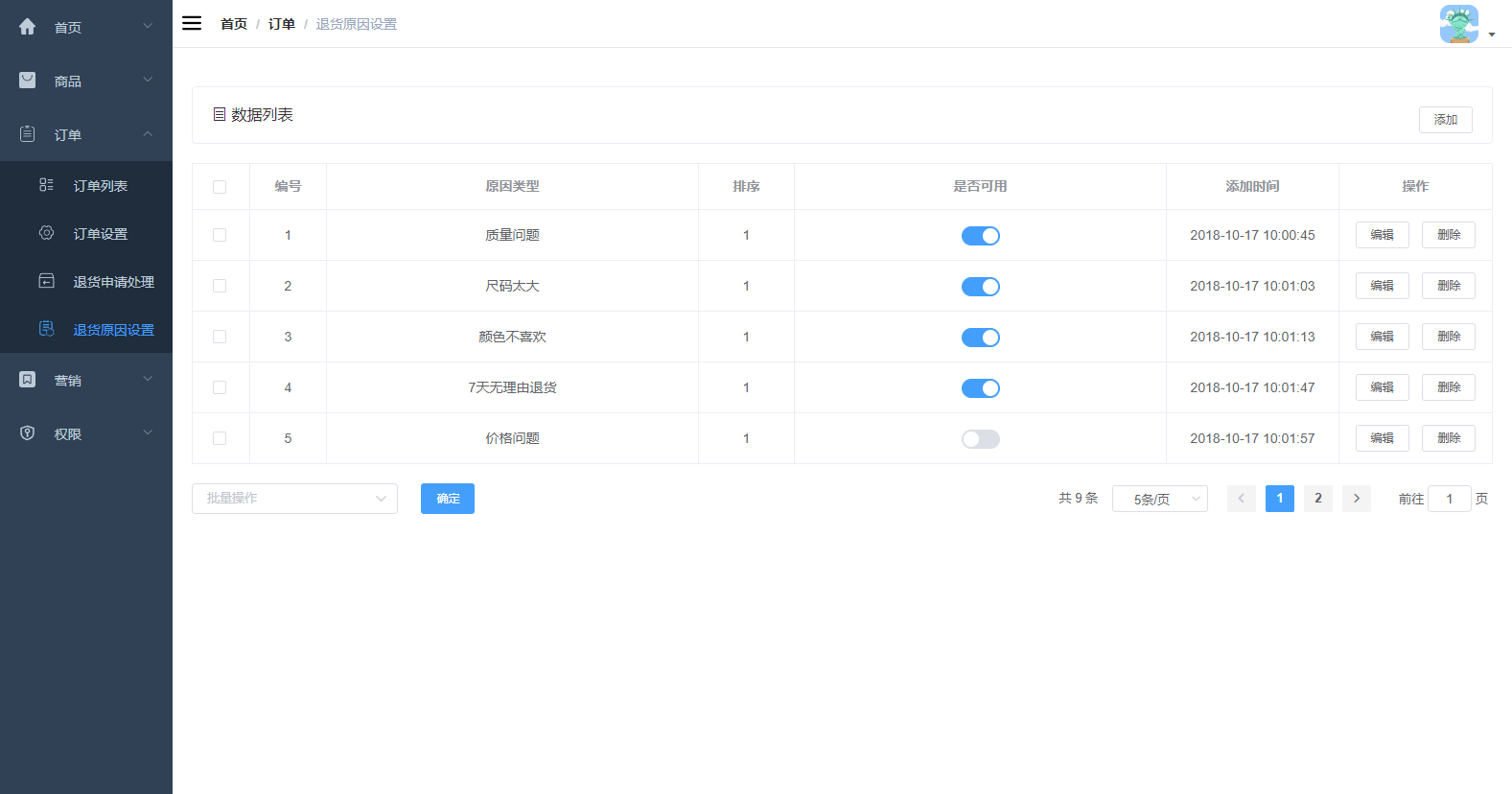
退货原因设置
后台管理员还可以对退货的原因进行设置,以便前台用户退货是进行选择。
前台商城系统
我们将以mall项目的核心订单流程为例,来介绍下前台商城系统中的订单功能。
流程示意图
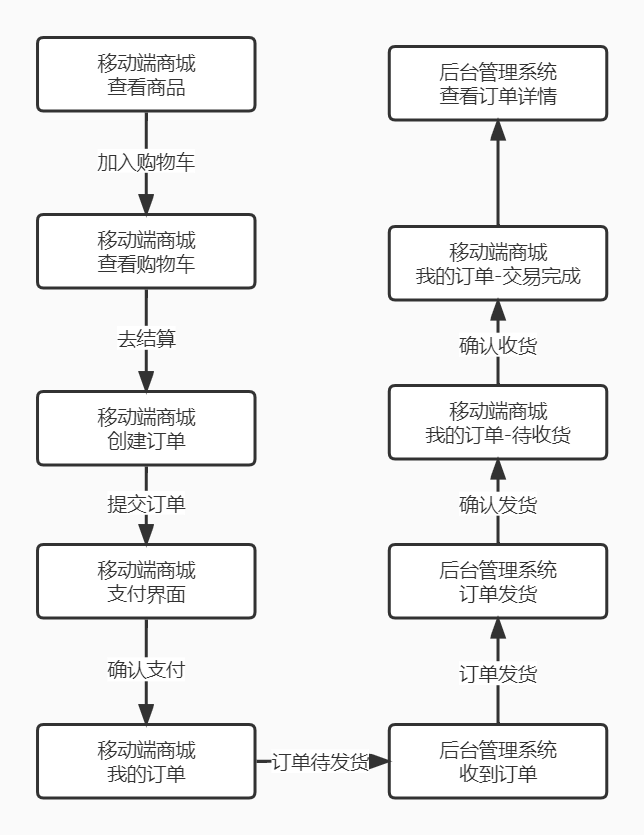
前台商城系统从加入购物车到完成订单的整个流程可以参考下图。
订单流程
- 前台会员可以在前台商城中查看商品;

- 前台会员点击加入购物车后查看购物车;

- 前台会员点击去结算后创建订单;

- 前台会员点击去结算后跳转到支付界面;

- 前台会员确认支付后跳转到我的订单界面;

- 后台管理系统收到订单;

- 后台管理员点击订单发货进行发货操作;

- 确认发货后,前台商城订单状态变为待收货;

- 前台会员确认收货后,订单状态变为交易完成;

- 后台管理系统可查看订单详情。

功能整理
对于订单模块的功能,我这里整理了一张思维导图方便大家查看,主要是整理了下有哪些功能以及功能需要涉及哪些字段。

数据库设计
根据我们的功能设计和整理好的思维导图,就可以进行数据库设计了,这里是mall项目订单模块的数据库设计图。

接口设计
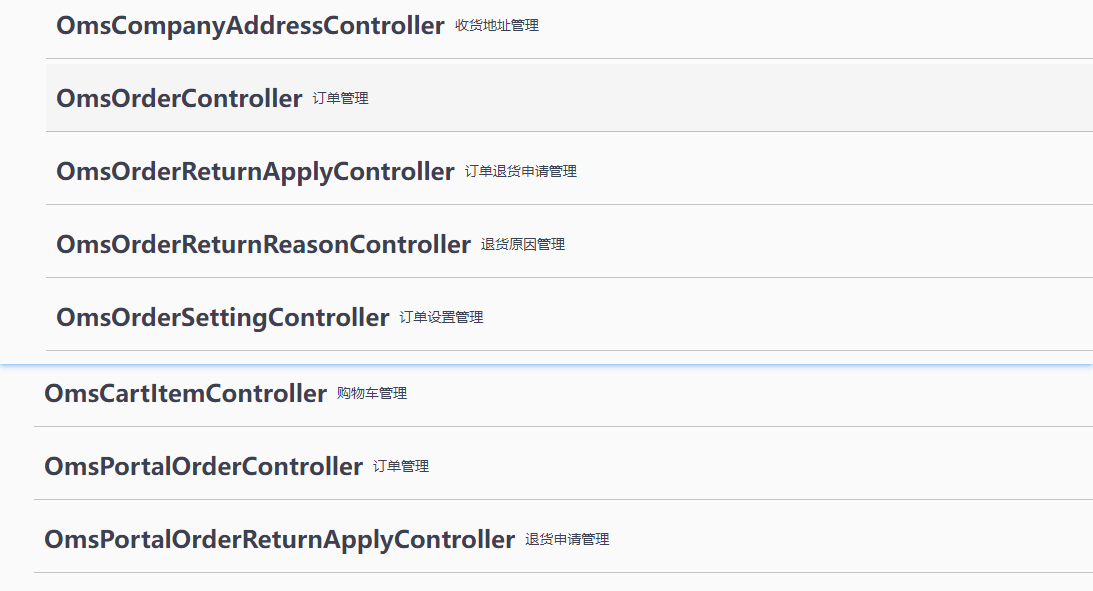
对于mall项目中订单模块的接口设计,大家可以参考项目的Swagger接口文档,以Oms开头的接口就是订单模块对应的接口。
总结
今天介绍了下mall项目中订单模块的功能设计、数据库设计和接口设计,由于很多项目中都会涉及到订单功能,掌握订单功能的设计还是非常有必要的!
项目源码地址
https://github.com/macrozheng/mall
相关文章:

订单系统就该这么设计,稳的一批~
订单功能作为电商系统的核心功能,由于它同时涉及到前台商城和后台管理系统,它的设计可谓是非常重要的。就算不是电商系统中,只要是涉及到需要交易的项目,订单功能都具有很好的参考价值,说它是通用业务功能也不为过。今…...

Agents改变游戏规则,亚马逊云科技生成式AI让基础模型加速工作流
最近,Stability AI正式发布了下一代文生图模型——Stable Diffusion XL 1.0这次的1.0版本是Stability AI的旗舰版生图模型,也是最先进的开源生图模型。 在目前的开放式图像模型中,SDXL 1.0是参数数量最多的。官方表示,这次采用的…...
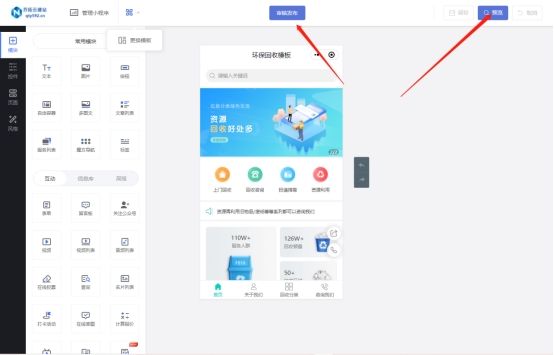
详细教程:如何搭建废品回收小程序
废品回收是一项环保举措,通过回收和再利用废弃物品,可以减少资源浪费和环境污染。近年来,随着智能手机的普及,小程序成为了推广和运营的重要工具。本文将详细介绍如何搭建一个废品回收小程序。 1. 进入乔拓云网后台 首先…...

什么是双亲委派机制?
什么是双亲委派机制? Parent Delegation Model ,直译过来可能叫做父级委托模型更容易理解 类的加载过程 Java 编译器将 Java源文件编译成.class 文件再由 JVM 加载 .class 文件到内存中JVM 装载完成后得到一个 Class 字节码对象拿到字节码对象之后 &a…...

Mageia 9 RC1 正式发布,Mandriva Linux 发行版的社区分支
导读Mageia 9 首个 RC 已发布。公告写道,自 2023 年 5 月发布 beta 2 以来,Mageia 团队一直致力于解决许多顽固问题并提供安全修复和新特性。 新版本的控制中心添加了用于删除旧内核的新功能,该功能在 Mageia 9 中默认自动启用,用…...

ChatGPT: 人机交互的未来
ChatGPT: 人机交互的未来 ChatGPT背景ChatGPT的特点ChatGPT的应用场景结论 ChatGPT ChatGPT是一种基于大数据和机器学习的人工智能聊天机器人模型。它由国内团队发明、开发,并被命名为Mental AI。ChatGPT的目标是通过模拟自然对话的方式,提供高效、智能…...
Linux 常用操作命令
Linux简介及Ubuntu安装 Linux,免费开源,多用户多任务系统。基于Linux有多个版本的衍生。RedHat、Ubuntu、Debian 安装VMware或VirtualBox虚拟机。具体安装步骤,找百度。 再安装Ubuntu。具体安装步骤,找百度。 常用指令 ls …...

24届近5年重庆邮电大学自动化考研院校分析
今天给大家带来的是重庆邮电大学控制考研分析 满满干货~还不快快点赞收藏 一、重庆邮电大学 学校简介 重庆邮电大学简称"重邮",坐落于直辖市-重庆市,入选国家"中西部高校基础能力建设工程”、国家“卓越工程师教育培养计划…...

如何对oracle和mysql进行 分区分表
前提:使用自带的分区和分表机制进行操作 oracle,mysql分区分表 分区 分区是一种将一个大的表或索引分割成多个小的部分的技术,每个部分称为一个分区。分区可以提高数据的管理和查询效率,因为可以根据不同的条件对不同的分区进行操作&#x…...
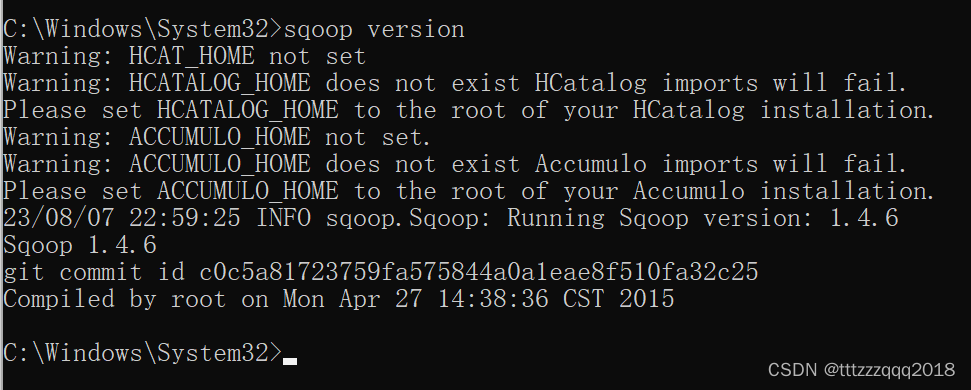
Windows下安装Sqoop
Windows下安装Sqoop 一、Sqoop简介二、Sqoop安装2.1、Sqoop官网下载2.2、Sqoop网盘下载2.3、Sqoop安装(以version:1.4.7为例)2.3.1、解压安装包到 D:\bigdata\sqoop\1.4.7 目录2.3.2、新增环境变量 SQOOP_HOME2.3.3、环境变量 Path 添加 %SQO…...
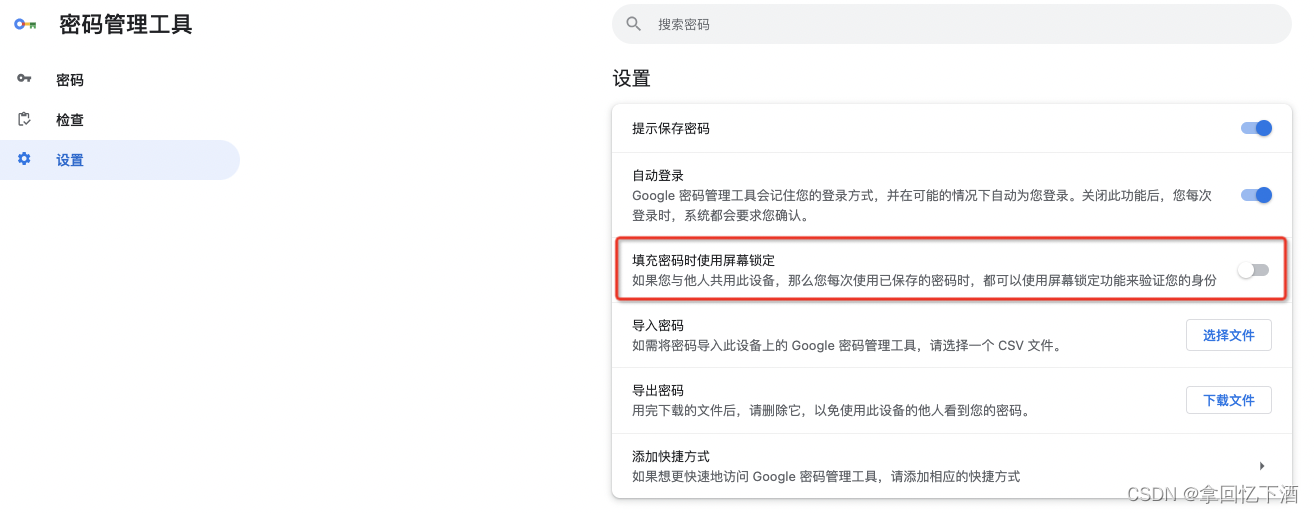
Chrome 谷歌浏览器,自动填充密码,提示需要输入电脑开机密码问题
我们在使用浏览器访问各个网站时,经常会保存密码。在下一次访问时,直接使用保存的密码填充,简单方便。 但是突然有一天(怀疑是谷歌浏览器更新导致的),每次使用密码填充时,都有如下拦截 拦截提…...
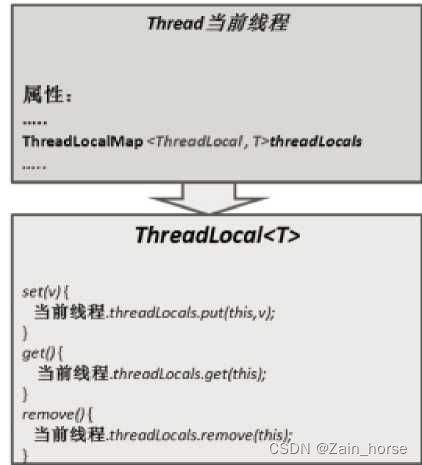
Java技术整理(3)—— 多线程并发篇
1、Java 线程实现/创建方式 (1)继承Thread类 Thread类本质上是实现了Runnable接口的实例,代表一个线程的实例,通过start()启动,自动执行run()方法。 (2)实现Runnable接口 Runnable是一个没有…...

2023热门跨境电商平台哪个入驻条件适合新手?
一、 Shopee 1.平台简介:东南亚最大跨境电商平台,覆盖新加坡、马来西亚、菲律宾、泰国、越南、巴西等十余个市场。 2.平台优势:流量大、物流快、东南亚市场前景好 3.入驻要求:企业或个体营业执照其他电商平台经验 4.平台费用&…...

【MFC】05.MFC第一大机制:程序启动机制-笔记
MFC程序开发所谓是非常简单,但是对于我们逆向人员来说,如果想要逆向MFC程序,那么我们就必须了解它背后的机制,这样我们才能够清晰地逆向出MFC程序,今天这篇文章就来带领大家了解MFC的第一大机制:程序启动机…...

小程序动画 animation 的常规使用
公司小程序项目比较多,最近正好有时间看一下小程序的动画,同时记录一下我的学习过程;看到这个文章的,我建议你之间去小程序后台:https://developers.weixin.qq.com/miniprogram/dev/api/ui/animation/wx.createAnimati…...

Swift 周报 第三十四期
文章目录 前言新闻和社区iPhone Pro 要提价!新款 iPhone 或会使用 USB-C 充电器,边框更薄与 App Store 专家会面交流让你的 App 和游戏在 visionOS 模拟器外更进一步 提案通过的提案正在审查的提案 Swift论坛推荐博文话题讨论关于我们 前言 本期是 Swif…...
[虚幻引擎] UE DTBase64 插件说明 使用蓝图对字符串或文件进行Base64加密解密
本插件可以在虚幻引擎中使用蓝图对字符串,字节数组,文件进行Base64的加密和解密。 目录 1. 节点说明 String To Base64 Base64 To String Binary To Base64 Base64 To Binary File To Base64 Base64 To File 2. 案例演示 3. 插件下载 1. 节点说…...

Jmeter组件作用域及执行顺序
目录 一、Jmeter八大可执行元件 二、组件执行顺序 三、组件作用域 四、特殊说明 一、Jmeter八大可执行元件 配置元件---Config Element 用于初始化默认值和变量,以便后续采样器使用。配置元件大其作用域的初始阶段处理,配置元件仅对其所在的测试树分…...

题目:2309.兼具大小写的最好英文字母
题目来源: leetcode题目,网址:2309. 兼具大小写的最好英文字母 - 力扣(LeetCode) 解题思路: 遍历字符串以获得兼具大小写的英文字母,然后返回最大者或空串即可。 解题代码: c…...
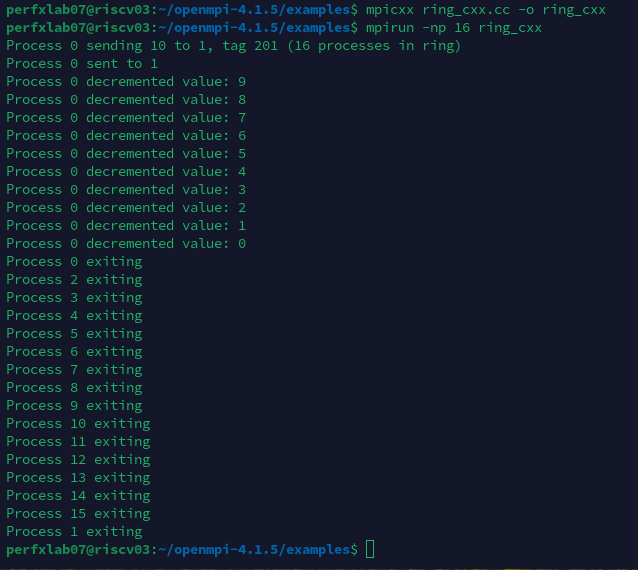
RISC-V公测平台发布:如何在SG2042上玩转OpenMPI
About HS-2 HS-2 RISC-V通用主板是澎峰科技与合作伙伴共同研发的一款专为开发者设计的标准mATX主板,它预装了澎峰科技为RISC-V高性能服务器定制开发的软件包,包括各种标准bencmark、支持V扩展的GCC编译器、计算库、中间件以及多种典型服务器应用程序。…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...
