扩展卡尔曼滤波器代码
文章目录
- 前言
- 问题
- 状态向量和观测向量
- 加性噪声的形式
- 状态方程及求导
- 观测方程及求导
- 状态初始化
- 过程噪声和观测噪声
- 卡尔曼滤波过程
- code
前言
卡尔曼滤波器在1960年被卡尔曼发明之后,被广泛应用在动态系统预测。在自动驾驶、机器人、AR领域等应用广泛。卡尔曼滤波器使用类似马尔可夫链的性质,假设系统状态只与上一时刻的系统状态有关。基础的卡尔曼滤波器使用线型方程对系统状态进行建模。为了能够应用到非线性系统,扩展卡尔曼滤波器利用泰勒展开,并只保留一次项,抛弃高次项,将非线性关系近似为线性关系。
问题
假设有一个小车从原点出发,每个时间间隔ΔT,车上的传感器可以输出车此时的速度ωt 和角速度ωt。同时,在原点处有一个探测器,同样可以每个ΔT的时间间隔,探测出车辆距离原点的距离dt。 我们希望能够求出小车每一时刻对应的x轴和y轴坐标at , bt
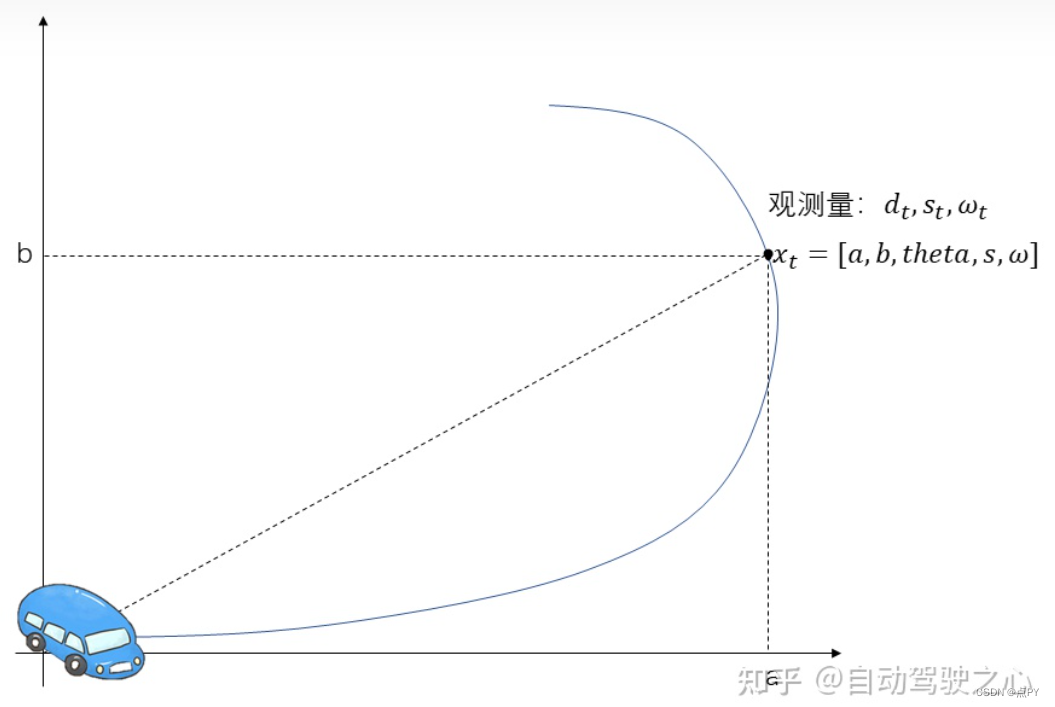
状态向量和观测向量
我们另小车每一时刻的x,y坐标、此时小车的车身角度,速度和角速度这5个状态当作状态向量,于是
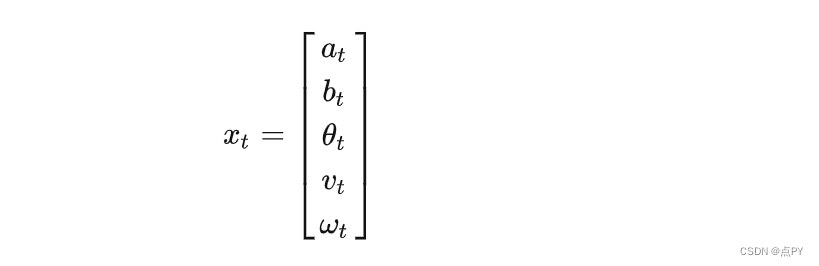
同时,另观测向量为距离原点距离的平方、速度、角速度,于是

加性噪声的形式
为了简化计算过程,我们这里将噪声项提到非线性方程外面,变成加性噪声的形式。
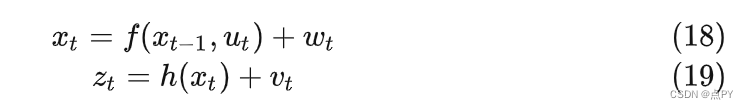
状态方程及求导
小车的x坐标等于上一时刻的x坐标以及这个时间段小车行使过的距离在x轴的投影。小车在每个时间段形式的距离为
v*ΔT;距离在x轴的投影相当于乘上cos(θ)。y坐标同理。角度则是每一时刻的角速度积分。于是,我们可以写出状态方程: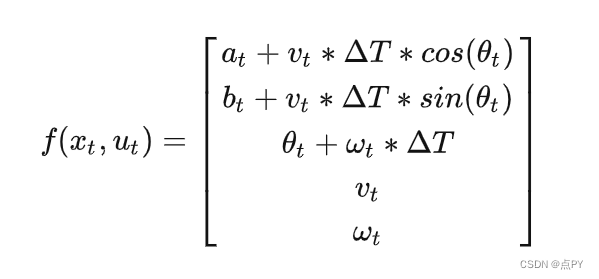
将函数f相对于状态向量xt求偏导数,可以得到
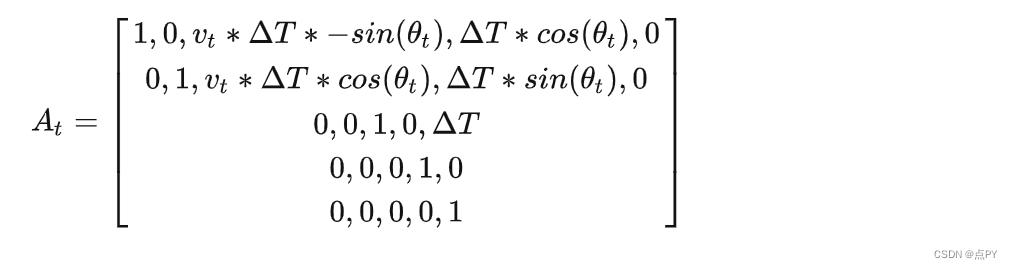
观测方程及求导
我们将小车与原点距离的平方、速度、角速度作为观测向量,即
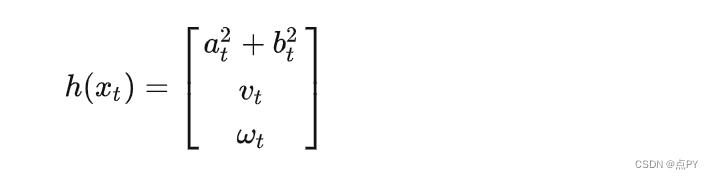
将上述方程对状态方程求偏导数可以得到
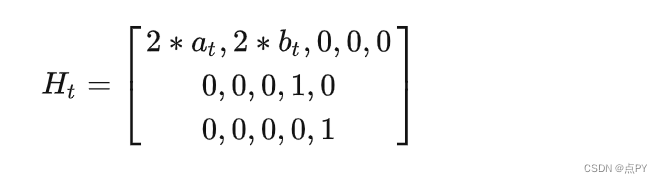
状态初始化
系统状态我们可以简单以全0向量作为初始值,即

另一个需要初始化的值是状态向量协方差矩阵P0。经过实验发现在滤波过程对P0的值似乎有点敏感,主要是不能只有对角线有值。实际上,如果在实际应用中,可以先采集一段数据计算出各个变量的初始值。这里将P0设为如下值

过程噪声和观测噪声
过程噪声的协方差和观测噪声的协方差矩阵我们设置为一个较小的值即可。只不过这里的Q矩阵似乎比较敏感。而且由于我们用了速度和角速度做积分,而另外一个观测量距离并不能为角度提供更多的信息。因此,对于角度,这里并不能得到比简单的积分好很多的结果。
# 过程噪声的协方差,需要调整的参数
Q = np.array([[0.01, 0, 0, 0, 0],[0, 0.01, 0, 0, 0],[0, 0, 0.0001, 0, 0],[0, 0, 0, 0.01, 0],[0, 0, 0, 0, 0.01]
])# 观测噪声协方差矩阵
R = np.array([[0.0001, 0, 0],[0., 0.0001, 0],[0, 0, 0.0001]
]) # 观测噪声的协方差,需要调整的参数
卡尔曼滤波过程
有了上面的雅各比矩阵推导,就可以利用公式(13-17)进行滤波过程。过程只用了到一些矩阵乘法,十分简单。具体可以看代码。

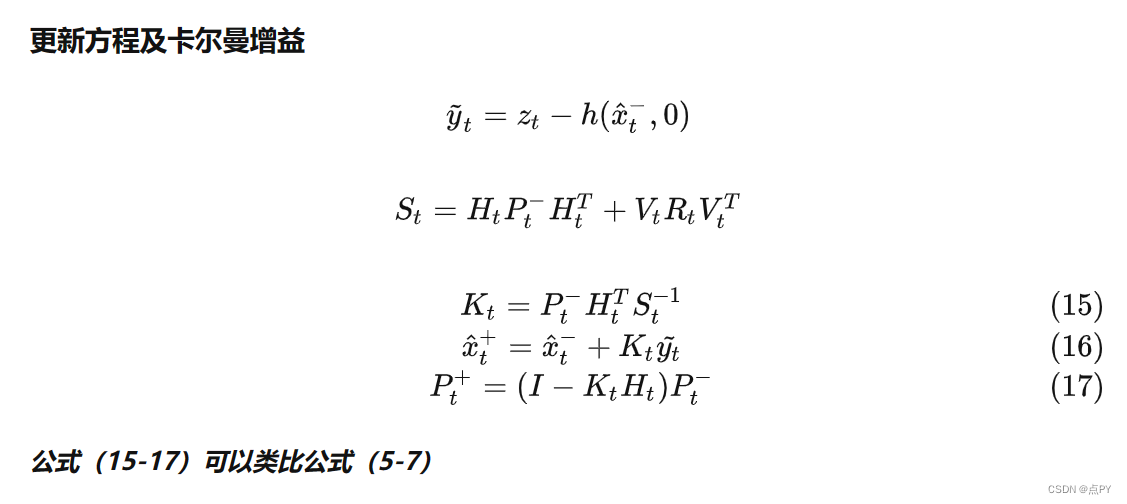
code
https://github.com/zeal-up/KalmanFilterTutorial
相关文章:
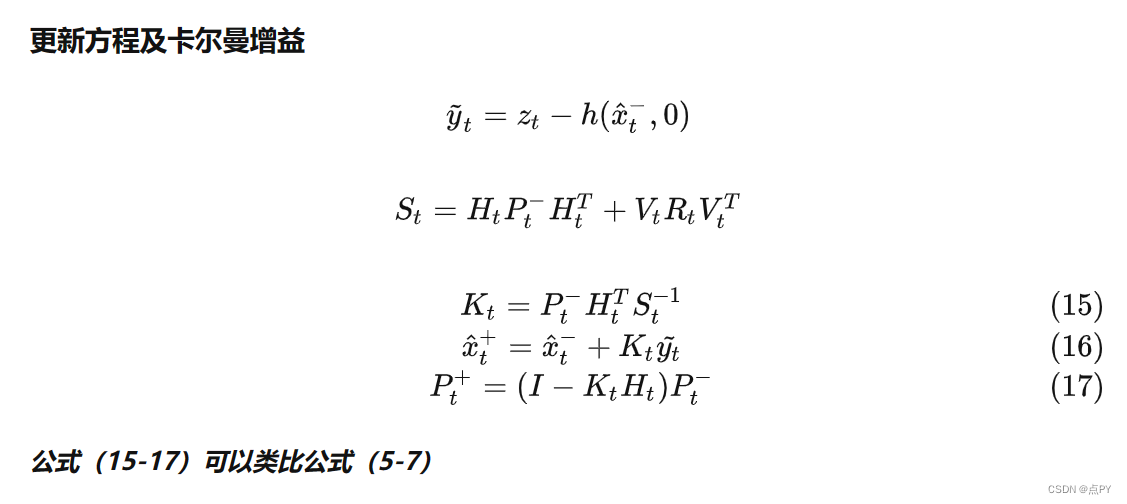
扩展卡尔曼滤波器代码
文章目录 前言问题状态向量和观测向量加性噪声的形式状态方程及求导观测方程及求导状态初始化过程噪声和观测噪声卡尔曼滤波过程code 前言 卡尔曼滤波器在1960年被卡尔曼发明之后,被广泛应用在动态系统预测。在自动驾驶、机器人、AR领域等应用广泛。卡尔曼滤波器使…...

9:00开始面试,9:08就出来了,这问题问的实在是····
外包工作3年,今年裸辞跳槽,很幸运的是找到了下家,不过 自从加入到这家公司,每天不是在加班就是在加班的路上,薪资倒是给的不少,所以我也就忍了。没想到6月一纸通知,所有人都不许加班࿰…...

揭秘:5个美国程序员与日本程序员的差异
大家好,这里是程序员晚枫。想了解更多精彩内容,快来关注程序员晚枫 今天以美国和日本程序员为例,给大家分享一下国外程序员的生活。 以下是五个美国程序员和日本程序员的的区别: 工作方式:美国程序员通常更注重自由和…...

Springboot实现简单JWT登录鉴权
登录为啥需要鉴权? 登录需要鉴权是为了保护系统的安全性和用户的隐私。在一个 Web 应用中,用户需要提供一定的身份信息(例如用户名和密码)进行登录,登录后系统会为用户生成一个身份令牌(例如 JWT Token&am…...

C++设计模式创建型之工厂模式整理
一、工厂模式分类 工厂模式属于创建型模式,一般可以细分为简单工厂模式、工厂模式和抽象工厂模式。每种都有不同的特色和应用场景。 二、工厂模式详情 1、简单工厂模式 1)概述 简单工厂模式相对来说,在四人组写的《设计模式------可复用面…...
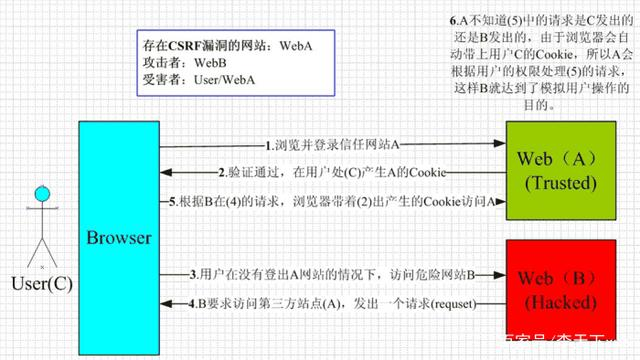
前端安全XSS和CSRF讲解
文章目录 XSSXSS攻击原理常见的攻击方式预防措施 CSRFCSRF攻击原理常见攻击情景预防措施: CSRF和XSS的区别 XSS 全称Cross Site Scripting,名为跨站脚本攻击。为啥不是单词第一个字母组合CSS,大概率与样式名称css进行区分。 XSS攻击原理 不…...

本地化部署自建类ChatGPT服务远程访问
本地化部署自建类ChatGPT服务远程访问 文章目录 本地化部署自建类ChatGPT服务远程访问前言系统环境1. 安装Text generation web UI2.安装依赖3. 安装语言模型4. 启动5. 安装cpolar 内网穿透6. 创建公网地址7. 公网访问8. 固定公网地址 🍀小结🍀 前言 Te…...
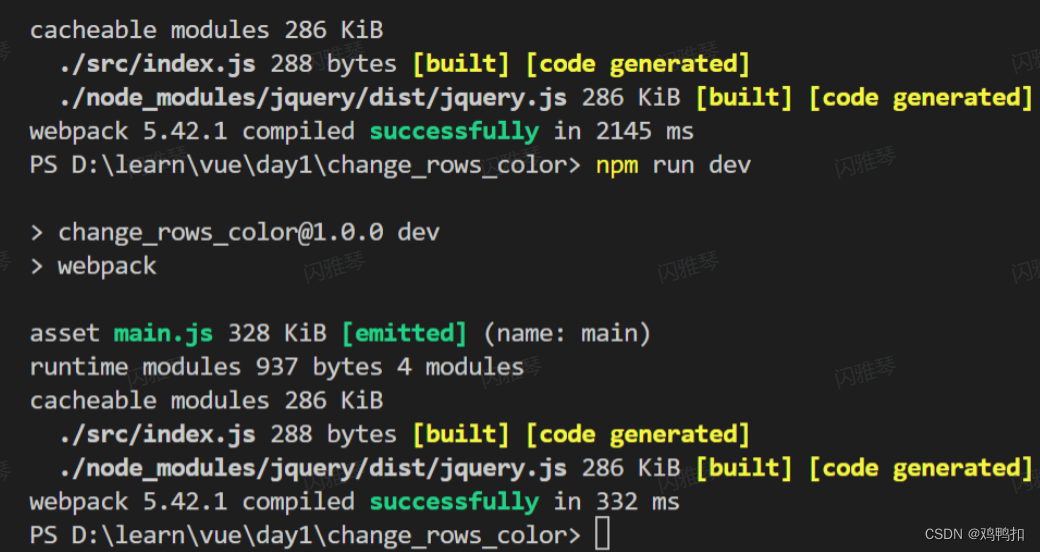
一、Webpack相关(包括webpack-dev-server用以热更新和html-webpack-plugin)
概念与功能: webpack是前端项目工程化的具体解决方案。它提供了友好的前端模块化开发支持,以及代码压缩混淆、处理浏览器端JavaScript的兼容性、性能优化等强大的功能。 快速上手:隔行变色 -S实际是--save的简写,表示安装的第三方…...
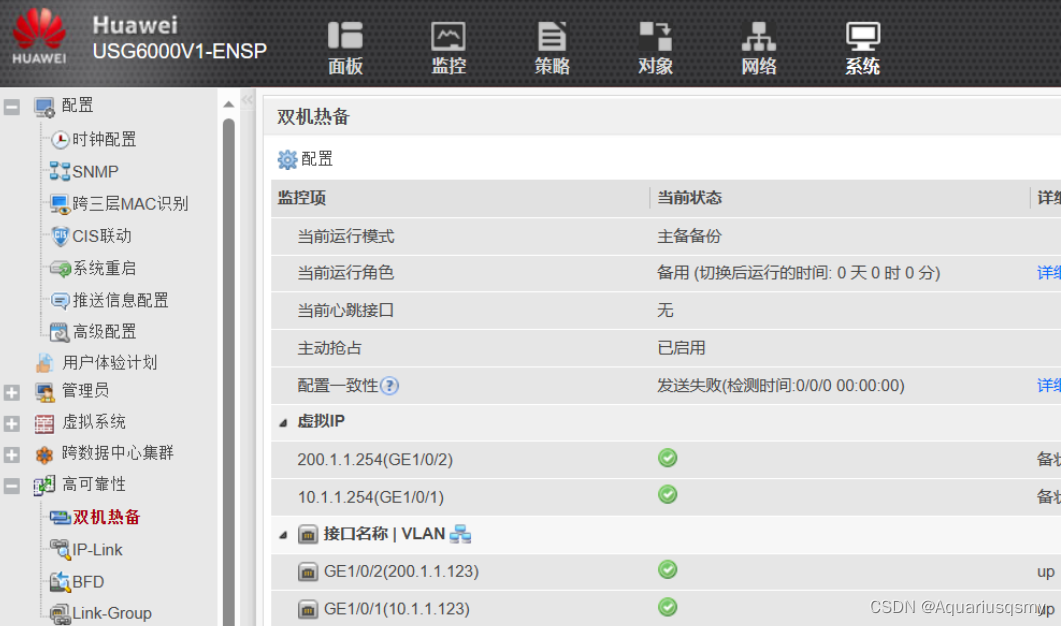
安全防御(3)
1.总结当堂NAT与双机热备原理,形成思维导图 2.完成课堂nat与双机热备试验 引用IDS是指入侵检测系统,它可以在网络中检测和防御入侵行为。IDS的签名是指根据已知入侵行为的特征制定的规则,用于检测和警告可能存在的入侵行为。签名过滤器可以根…...

AR远程专家指导在汽车改装上的应用有哪些?
随着科技的不断发展,AR增强现实技术逐渐走进了我们的生活。加上商贸国际化,远程协同纵深到制造生产的更多环节,研发协同、工艺优化等场景复杂、跨层级、需要频繁沟通确认的流程正通过AR应用实现全面远程化的过渡,在汽车行业&#…...
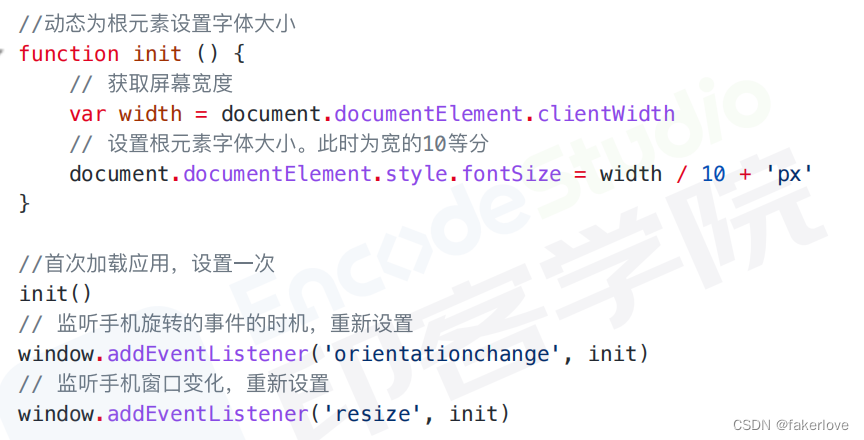
css-3:什么是响应式设计?响应式的原理是什么?如何做?
1、响应式设计是什么? 响应式网站设计(Responsive WEB desgin)是一个网络页面设计布局,页面的设计与开发应当根据用户行为以及设备环境(系统平台、屏幕尺寸、屏幕定向等)进行相应的相应和调整。 描述响应式…...

Armstrong数,n位数等于其各位数的n次方之和。
//Armstrong数具有以下特征:一个n位数等于其各位数的n次方之和。 //例如:1531^35^33^3 16341^46^43^44^4 #include<stdio.h> #include<math.h> //实在不知道的暴力求解方法 int main() {//Armstrong数具有以下特征:一个…...

blender的下载安装和配置中文环境
引言 在3D建模和动画设计领域,Blender 作为一款强大且免费的开源软件,一直以优秀的性能和对众多技术的支持赢得了大批用户的喜爱。然而,对于刚接触这款软件的用户而言,其安装和配置过程可能会带来一定困扰,尤其是在设…...
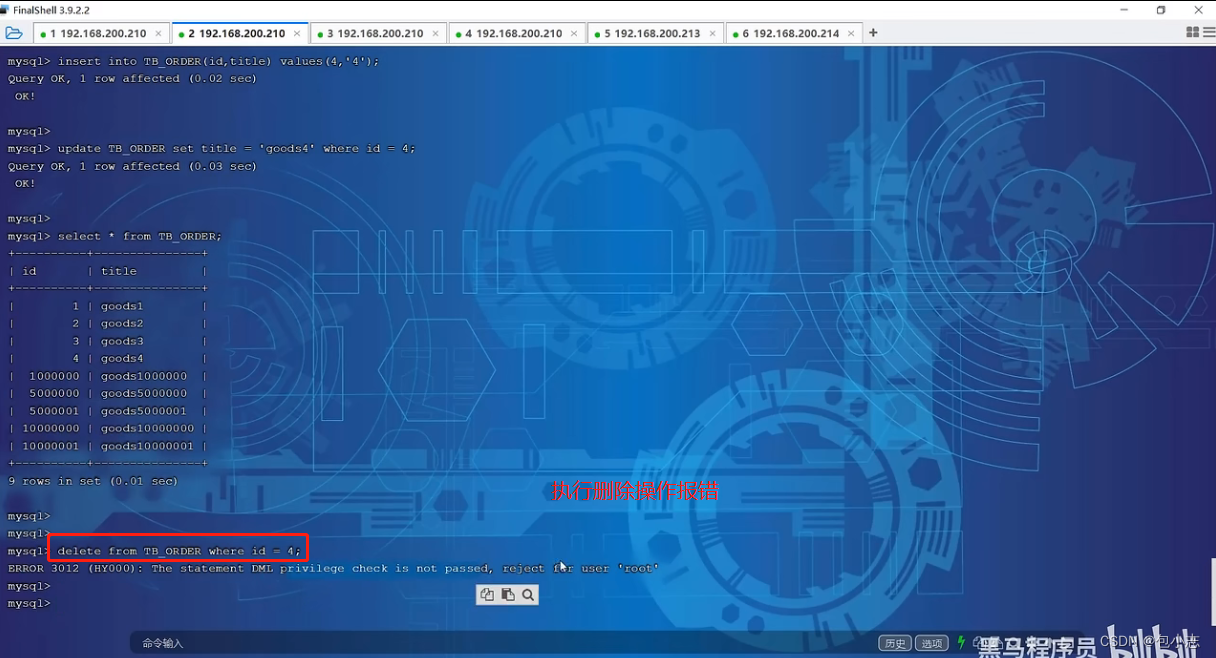
MyCat配置rule.xml、server.xml讲解
1. rule.xml分片规则配置文件 rule.xml中配置的主要就是拆分表的规则,rule.xml中主要包含两类标签 tableRule 和Function。 tableRule标签里面主要配置我们的分片规则,Function里面涉及的是分片规则里面所涉及的java类,都是在function中配置…...
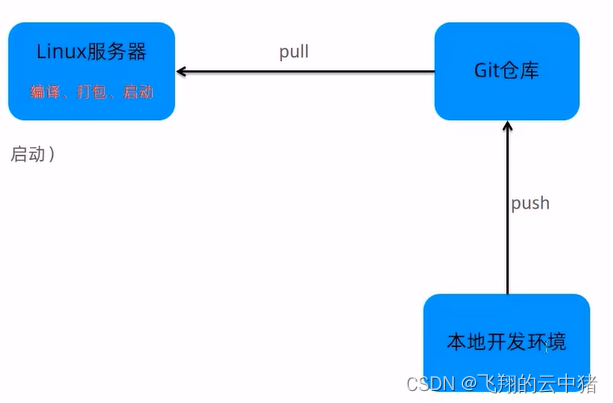
Linux项目部署
目录 一JAVAWeb环境的部署【安装JDK,MySQL数据库,Tomcat】 二.手工部署SpringBoot项目(写的最好的) 1.在IDEA中开发SpringBoot项目并打成jar包--点击右侧的Maven执行package命令 2.将jar包上传到Linux服务器 3.执行以下命令&a…...

案例:Docker 镜像的创建及使用(commit与dockerfile方式)
文章目录 1、commit方式创建镜像1.1、前期准备1.2、制成镜像1.3、启动镜像1.3.1、启动镜像启动nginx1.3.2、一个命令直接全部启动1.3.3、两种方式区别 1.4、commit创建镜像方式的本质 2、Dockerfile的使用2.1、Dockerfile指令2.2、nginx镜像制作案例2.3、查看构建历史ÿ…...
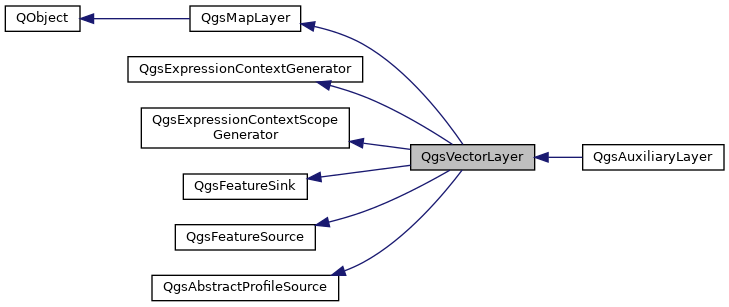
QGIS二次开发三:显示Shapefile
Shapefile 为 OGR 所支持的最重要的数据格式之一,自然可以被 QGIS 加载。那么该如何显示Shapefile呢? 一、先上代码 #include <qgsapplication.h> #include <qgsproviderregistry.h> #include <qgsmapcanvas.h> #include <qgsvec…...

FFmpeg中相关结构体介绍
AVFormatContext:此结构体存储音视频封装格式中包含的信息,并且这个结构体是贯穿整个播放流程的。在这个结构体中主要包含AVInputFormat,AVOutputFormat、AVStream等。 struct AVInputFormat *iformat; // 输入数据的封装格式 AVIOContext *…...
Llama 2 云端部署与API调用【AWS SageMaker】
Meta 刚刚发布了 Llama 2 大模型。如果你和我们一样,你一定会迫不及待地想要亲自动手并用它来构建。 推荐:用 NSDT设计器 快速搭建可编程3D场景。 使用任何类型的 LLM 进行构建的第一步是将其托管在某处并通过 API 使用它。 然后你的开发人员可以轻松地将…...
根文件系统制作
1.官网下载工具 制作工具:busybox https://busybox.net/downloads/ 2.制作根文件系统 2.1准备工作 a.把压缩包放在FSP1M目录下,并解压 2.2正式开始 2.2.1配置交叉编译工具链 1. 打开Makefile文件 2. 修改ARCH ?$(SUBARCH) …...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...
