LeetCode 130. 被围绕的区域
题目链接:130. 被围绕的区域
题目描述
给你一个 m x n 的矩阵 board ,由若干字符 ‘X’ 和 ‘O’ ,找到所有被 ‘X’ 围绕的区域,并将这些区域里所有的 ‘O’ 用 ‘X’ 填充。
示例1:

输入:board = [[“X”,“X”,“X”,“X”],[“X”,“O”,“O”,“X”],[“X”,“X”,“O”,“X”],[“X”,“O”,“X”,“X”]]
输出:[[“X”,“X”,“X”,“X”],[“X”,“X”,“X”,“X”],[“X”,“X”,“X”,“X”],[“X”,“O”,“X”,“X”]]
解释:被围绕的区间不会存在于边界上,换句话说,任何边界上的 ‘O’ 都不会被填充为 ‘X’。 任何不在边界上,或不与边界上的 ‘O’ 相连的 ‘O’ 最终都会被填充为 ‘X’。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。
示例2:
输入:board = [[“X”]]
输出:[[“X”]]
题目分析
可以先处理从边界向内蔓延的O,将这些O替换成其他字符,没有没替换的O就是被X围绕的O,然后整个遍历,将特殊字符替换为O,将被围绕的O替换为X。
代码
class Solution {public void solve(char[][] board) {if (board.length == 0) {return;}// 初始化长宽int m = board.length, n = board[0].length;// 遍历左右两边的边界for (int i = 0; i < m; i++) {dfs(board, i, 0);dfs(board, i, n - 1);}// 遍历上下边界,四个端点上次已经遍历过了for (int j = 1; j < n - 1; j++) {dfs(board, 0, j);dfs(board, m - 1, j);}// 遍历将 A 染为 O ,将 O 染为 Xfor (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (board[i][j] == 'A') {board[i][j] = 'O';} else if (board[i][j] == 'O') {board[i][j] = 'X';}}}}void dfs(char[][] board, int i, int j) {// 处理边界情况,如果为 O 则染为 Aif (i >= 0 && j >= 0 && i < board.length && j < board[0].length && board[i][j] == 'O') {board[i][j] = 'A';// 染色上下左右dfs(board, i + 1, j);dfs(board, i - 1, j);dfs(board, i, j + 1);dfs(board, i, j - 1);}}
}
相关文章:

LeetCode 130. 被围绕的区域
题目链接:130. 被围绕的区域 题目描述 给你一个 m x n 的矩阵 board ,由若干字符 ‘X’ 和 ‘O’ ,找到所有被 ‘X’ 围绕的区域,并将这些区域里所有的 ‘O’ 用 ‘X’ 填充。 示例1: 输入:board [[“…...
python中2等于2.0吗,python中【1:2】
本篇文章给大家谈谈python中2等于2.0吗,以及python中【1:2】,希望对各位有所帮助,不要忘了收藏本站喔。 变量和赋值 Python中的变量不需要声明, 直接定义即可. 会在初始化的时候决定变量的 “类型” 使用 来进行初始化和赋值操作 定义变量时…...
》)
【2023年11月第四版教材】《第2章-信息技术发展(第一部分)》
《第2章-信息技术发展(第一部分)》 章节说明1 计算机软硬件2 计算机网络2.1 网络的作用范围2.2 OSI模型2.3 广域网协议2.4 网络协议2.5 TCP/IP2.6 软件定义网络(SDN)2.7 第五代移动通信技术 章节说明 大部分为新增内容࿰…...

【CSS】说说对BFC的理解
目录 一、概念 二、BFC的布局规则 三、设置BFC的常用方式 四、BFC的应用场景 1、解决浮动元素令父元素高度坍塌的问题 2、解决非浮动元素被浮动元素覆盖问题 3、解决外边距垂直方向重合的问题 五、总结 一、概念 我们在页面布局的时候,经常出现以下情况&am…...

ES6学习-Class类
class constructor 构造方法 this 代表实例对象 方法之间不需要逗号分隔,加了会报错。 typeof Point // "function" Point Point.prototype.constructor // true类的数据类型就是函数,类本身就指向构造函数。 类的所有方法都定义在类的pr…...

C语言经典小游戏之扫雷(超详解释+源码)
“少年气,是历尽千帆举重若轻的沉淀,也是乐观淡然笑对生活的豁达!” 今天我们学习一下扫雷游戏怎么用C语言来实现! 扫雷小游戏 1.游戏介绍2.游戏准备3.游戏实现3.1生成菜单3.2游戏的具体实现3.2.1初始化棋盘3.2打印棋盘3.3布置雷…...
)
算法leetcode|67. 二进制求和(rust重拳出击)
文章目录 67. 二进制求和:样例 1:样例 2:提示: 分析:题解:rust:go:c:python:java: 67. 二进制求和: 给你两个二进制字符串 a 和 b &a…...
【ASP.NET MVC】第一个登录页面(8)
一、准备工作 先从网上(站长之家、模板之家,甚至TB)下载一个HTML模板,要求一整套的CSS和必要的JS,比如下图: 登录页面的效果是: 首页: 利用这些模板可以减少前台网页的设计——拿来…...

使用Openoffice或LibreOffice实现World、Excel、PPTX在线预览
使用Openoffice或LibreOffice实现World、Excel、PPTX在线预览 预览方案使用第三方服务使用前端库转换格式 jodconverterjodconverter概述主要特性OpenOfficeLibreOffice jodconverter的基本使用添加依赖配置创建DocumentConverter实例上传与转换预览启动上传与预览World 与Spri…...
没有object的rust怎么面向对象?)
20天学会rust(三)没有object的rust怎么面向对象?
面向对象我们都很熟悉,可以说它是一种软件开发最重要的编程范式之一,它将程序中的数据和操作数据的方法组织成对象。面向对象有几个重要特性: 封装、继承和多态,基于这些特性带来了在可重用性、可维护性、扩展性、可靠性的优点。 …...
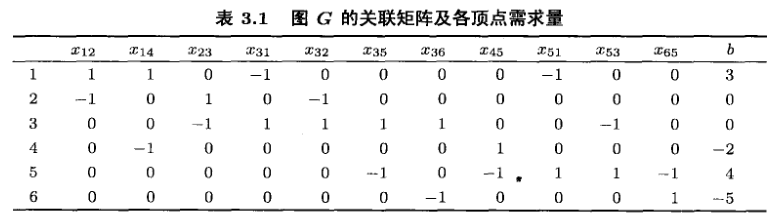
整数规划——第三章 全单模矩阵
整数规划——第三章 全单模矩阵 若线性规划问题的约束矩阵为全单模矩阵,则该问题可行域的顶点都是整数点,从而线性规划与整数规划的最优解相同。 3.1 全单模性与最优性 考虑线性整数规划问题: (IP) min c T x , s . t . A x ≤ b , x …...

数据结构和算法
数据结构和算法目录表 CCJava线性结构 1. 数组、单链表和双链表 2. Linux内核中双向链表的经典实现 数组、单链表和双链表 数组、单链表和双链表 栈 栈 栈 队列 队列 队列树形结构 二叉查找树 二叉查找树 二叉查找树 AVL树 AVL树 AVL树 伸展树 伸展树 伸展树 1. 红黑树(一)之…...
[Vulnhub] matrix-breakout-2-morpheus
目录 <1> 信息收集 <2> getshell <3> Privilege Escalation(提权) <1> 信息收集 nmap -sP 192.168.236.0/24 扫描一下靶机ip 靶机ip: 192.168.236.154 nmap -A -p 1-65535 192.168.236.154 扫描一下靶机开放哪些服务 开放…...
JDK, JRE和JVM之间的区别和联系
JDK, JRE和JVM是与Java编程语言相关的三个重要的概念,它们分别代表Java Development Kit(Java开发工具包)、Java Runtime Environment(Java运行时环境)和Java虚拟机(Java Virtual Machine)。它们…...
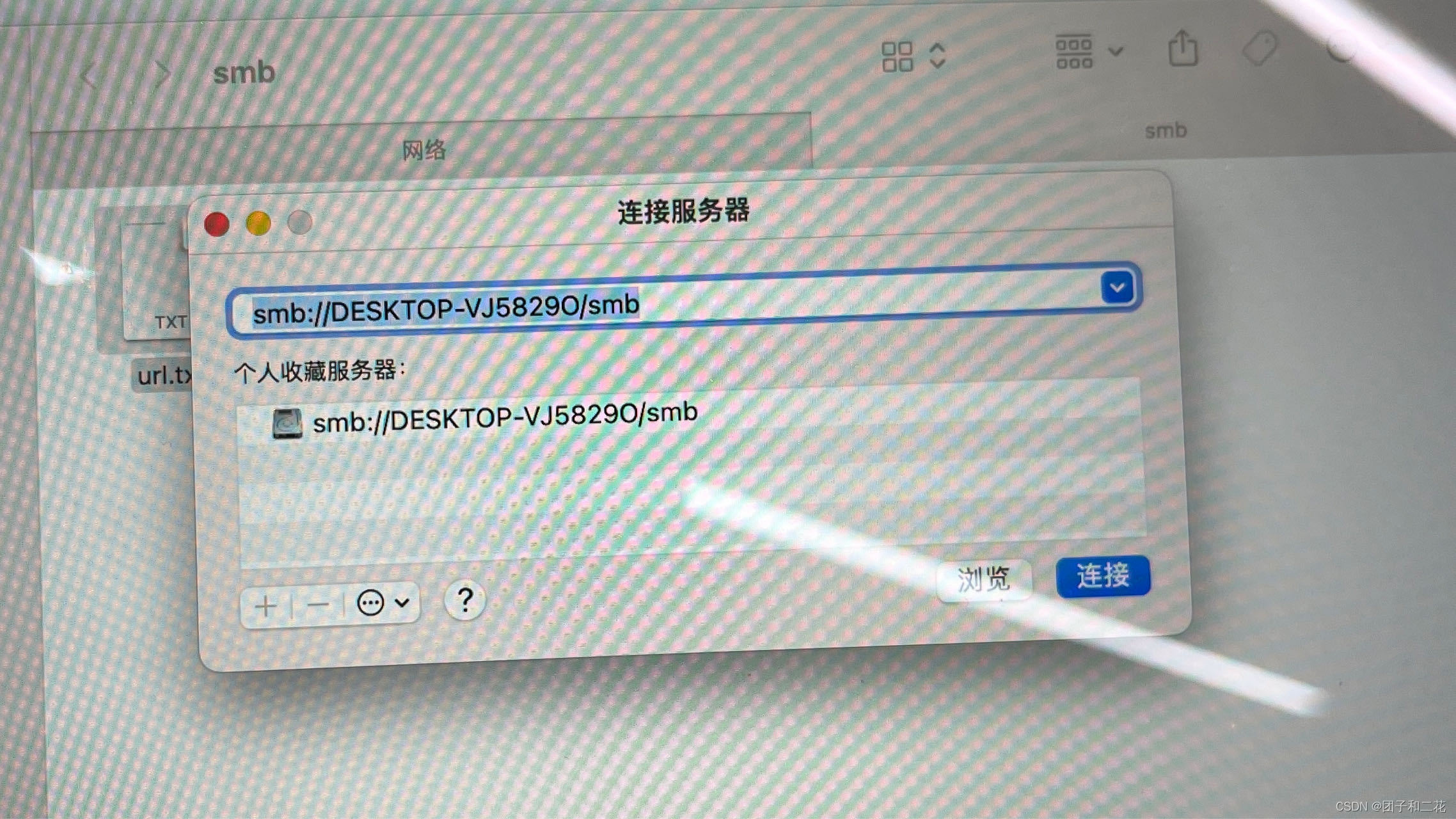
mac电脑访问windows共享文件夹连接不上(设置445端口)
前提:首先需要保证mac和windows都在同一局域网内,如果不在肯定是连不上的,就不用往下看了。 事情是这样的,公司入职发了mac电脑,但是我是window重度用户,在折腾mac的过程中,有许多文件需要从wi…...

metersphere性能压测执行过程
(1) 首先在controller层,通过RunTestPlanRequest接收请求参数 PostMapping("/run")public String run(RequestBody RunTestPlanRequest request) (2) 在PerformanceTestService中的run中进行具体的逻辑处理, 首先根据请求中ID来获取库中存储…...

揭秘Word高级技巧:事半功倍的文字处理策略
Microsoft Word是一款广泛使用的文字处理软件,几乎每个人都有使用过它的经历。但是,你是否知道Word中隐藏着许多高级技巧和功能,可以帮助你事半功倍地处理文字?在本文中,我们将揭秘一些Word的高级技巧,让你…...
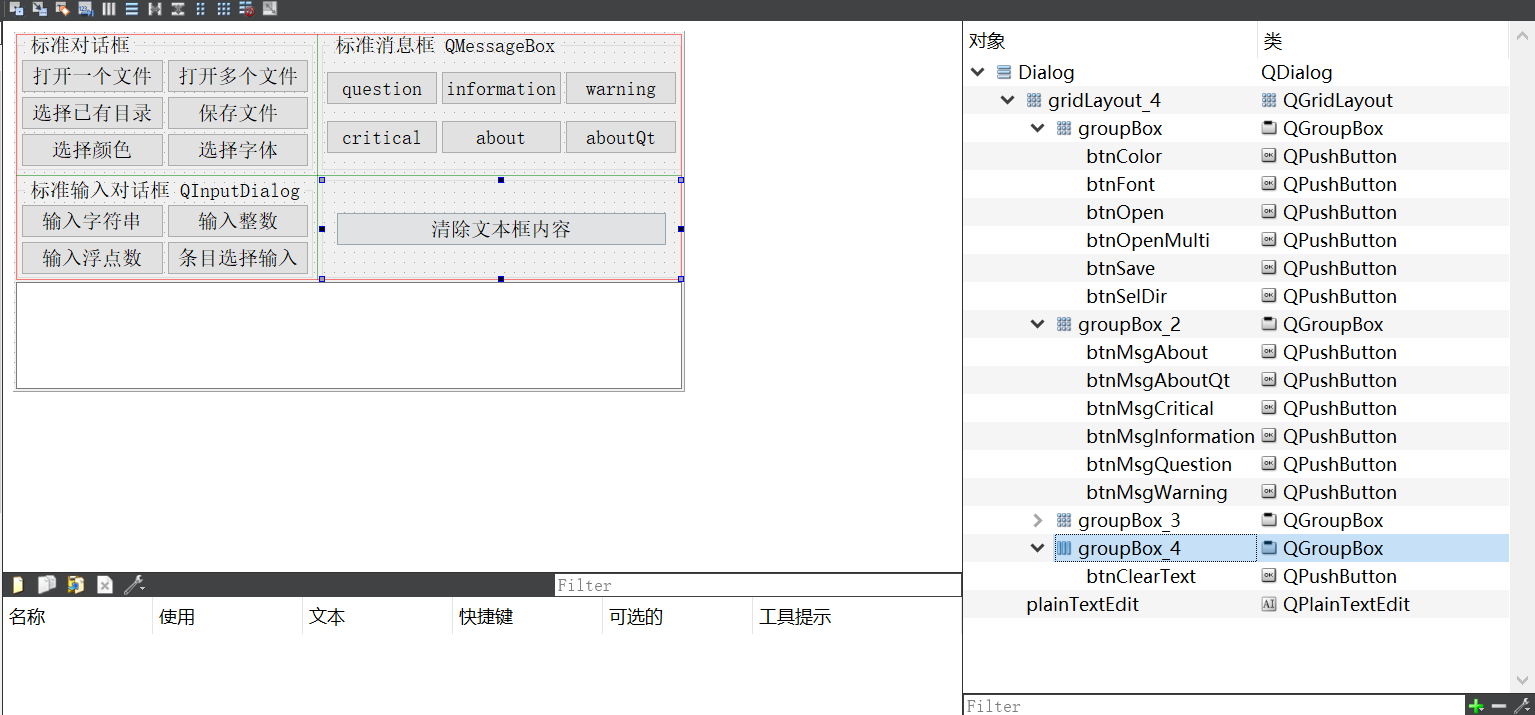
06-1_Qt 5.9 C++开发指南_对话框与多窗体设计_标准对话框
在一个完整的应用程序设计中,不可避免地会涉及多个窗体、对话框的设计和调用,如何设计和调用这些对话框和窗体是搞清楚一个庞大的应用程序设计的基础。本章将介绍对话框和多窗体设计、调用方式、数据传递等问题,主要包括以下几点。 Qt 提供的…...

模拟实现消息队列项目(系列7) -- 实现BrokerServer
目录 前言 1. 创建BrokerServer类 1.1 启动服务器 1.2 停止服务器 1.3 处理一个客户端的连接 1.3.1 解析请求得到Request对象 1.3.2 根据请求计算响应 1.3.3 将响应写回给客户端 1.3.4 遍历Session的哈希表,把断开的Socket对象的键值对进行删除 2. 处理订阅消息请求详解(补充) …...
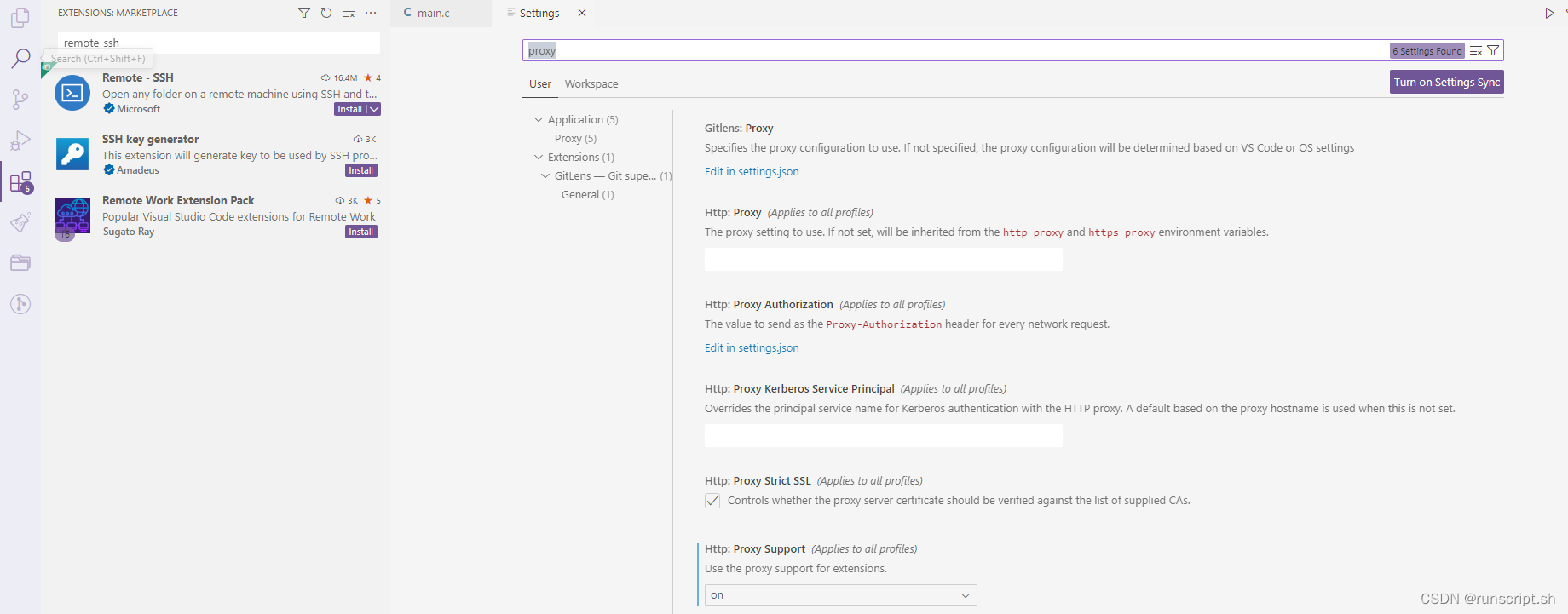
vscode插件不能搜索安装
1 现象 vscode搜索自己的插件,报错: Error while fetching extensions. HXR failed2 原因 之前用vscode开发golang语言,设置了proxy代理,所以导致错误,删除即可 重启vscode 3 结果...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...
