当前位置： 首页 > news >正文

在线高精地图生成算法调研

news 2026/3/27 6:05:21

1.HDMapNet

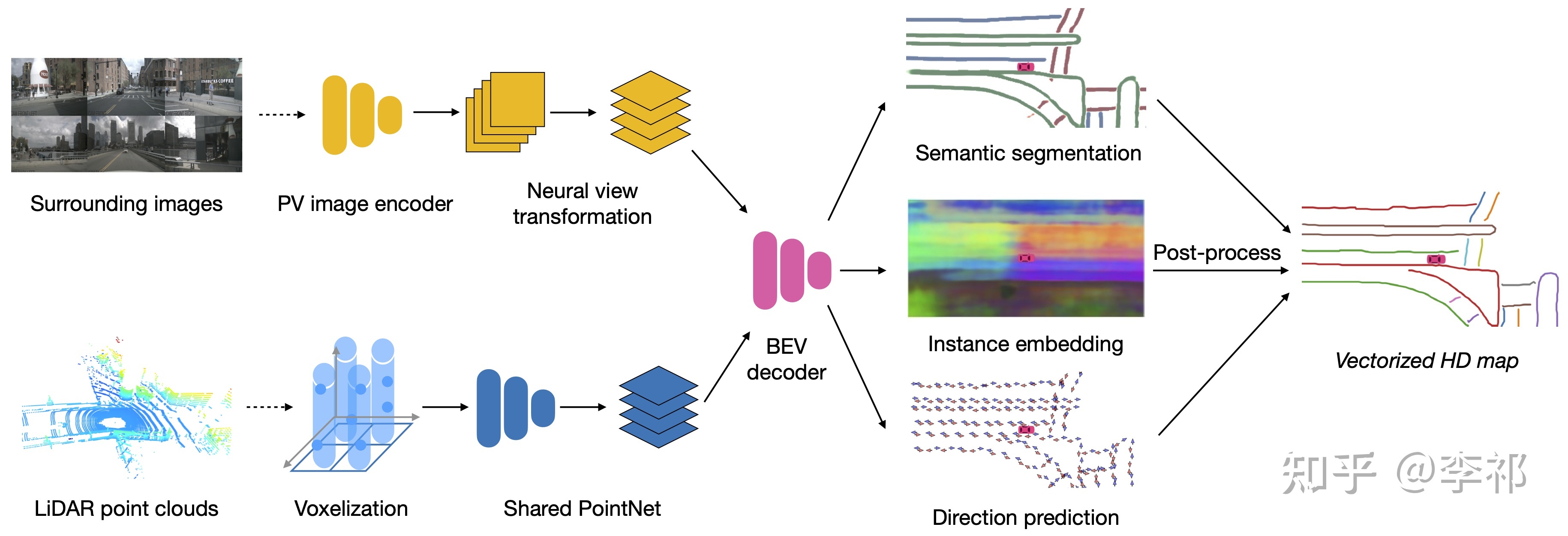
 整体的网络架构如图所示，最终的Decoder输出三个分支，一个语义分割，一个embedding嵌入分支，一个方向预测。然后通过后处理将这些信息处理成向量化的道路表示。

img2bev的方式之前有IPM，通过假设地面的高度都为0来完成转换，但是因为存在地面倾斜和车的颠簸，我们并不能保证车道线被正确投影到BEV上。而LSS的话，由于没有显式的深度作为监督，所以效果也不是很好。这里我们采用VPN的方式，使用全连接网络来学习如何进行视角变换。

埋坑：这里的后处理是如何进行一个向量化的道路表示？

2.MapTR

使用纯相机来生成在线高精地图，img2bev使用的地平线提出的GKT方法，对于BEV query，先通过内外参得到其在图像上的先验位置(可能对应多张图)，并提取附近w*h核区域的特征，然后和bev query做交叉注意力机制。

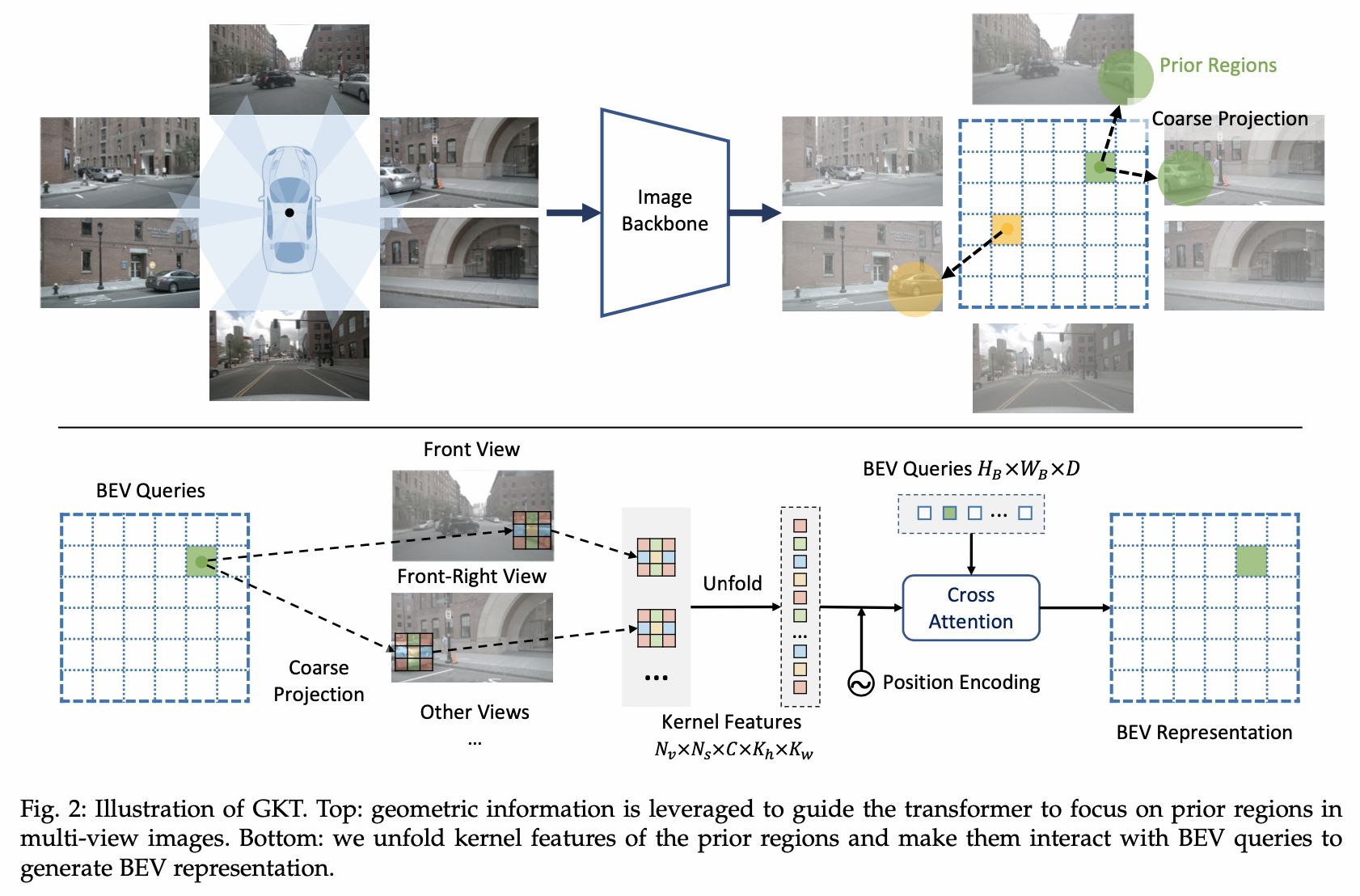
3.SuperFusion

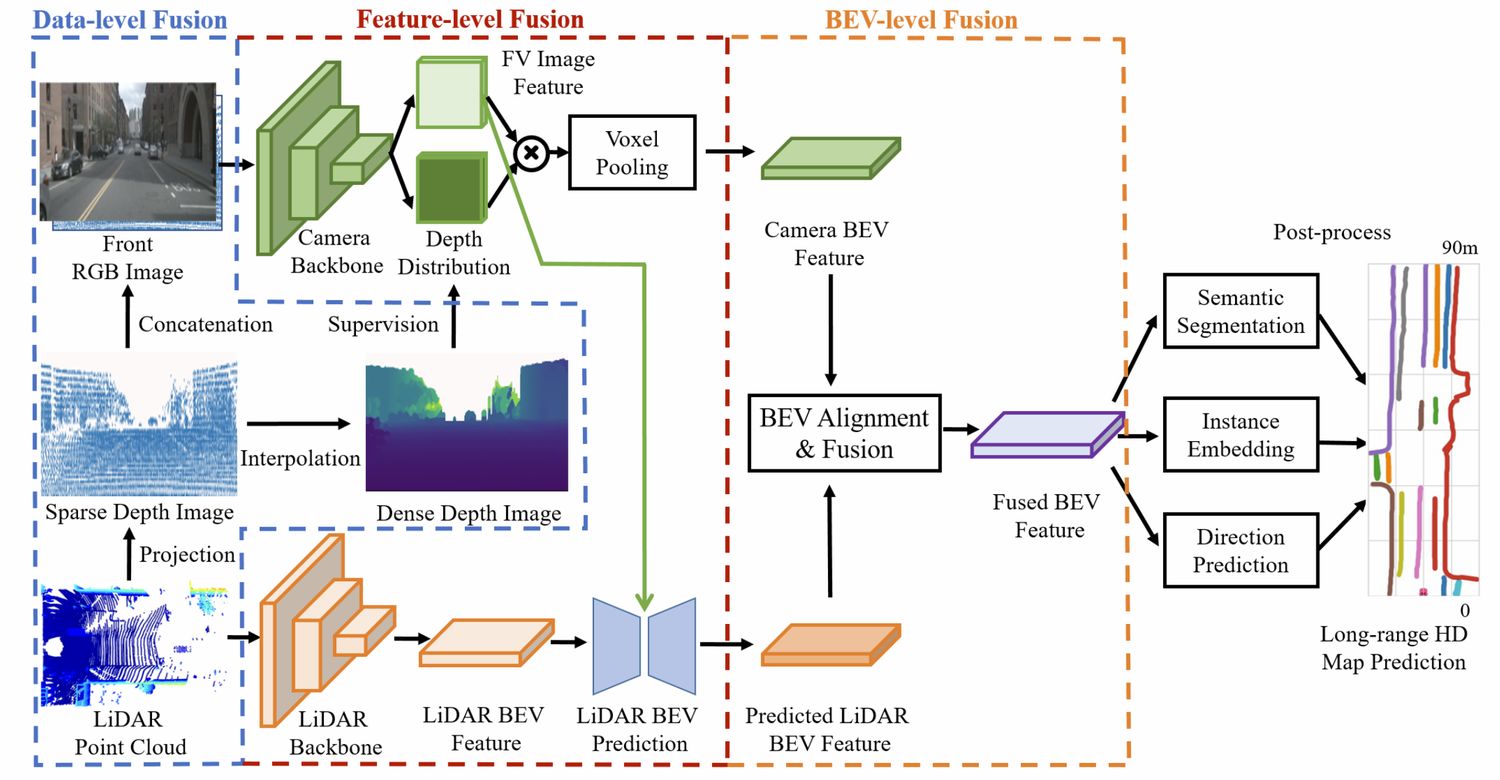
采用多层级的图像点云特征融合来做。

首先是数据层面的融合，先将点云投影到图像，然后稀疏深度与图像进行concate，同时利用双线性插值得到密集深度图，对LSS的深度估计进行监督。

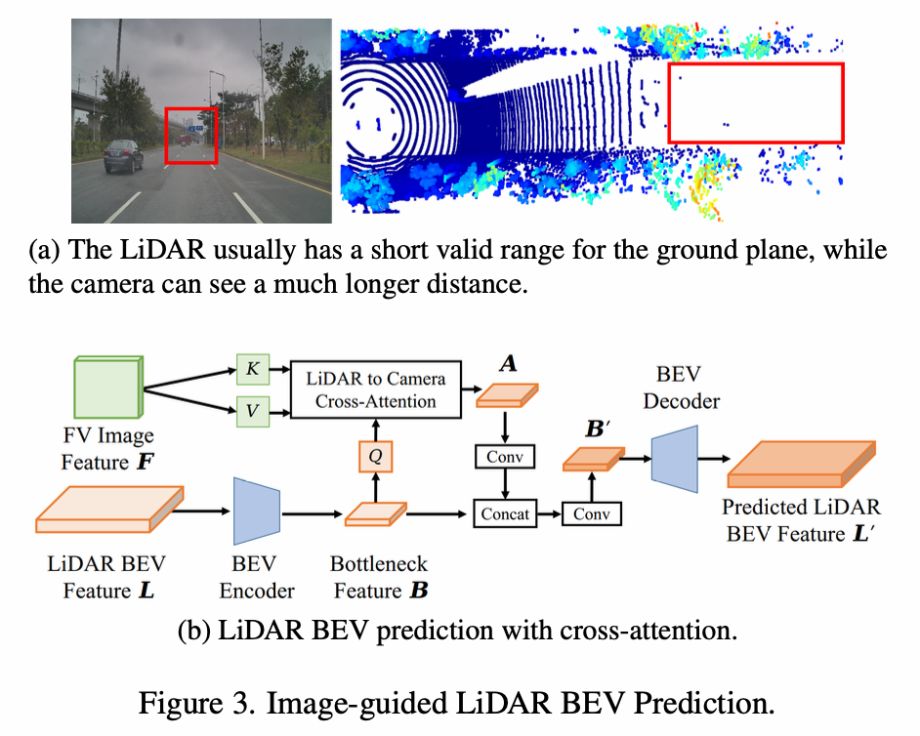
特征层面的融合，将点云的BEV特征作为Q去查询图像的特征，做cross-attention得到新的BEV特征，并通过一系列的卷积融合。得到点云BEV最终特征。

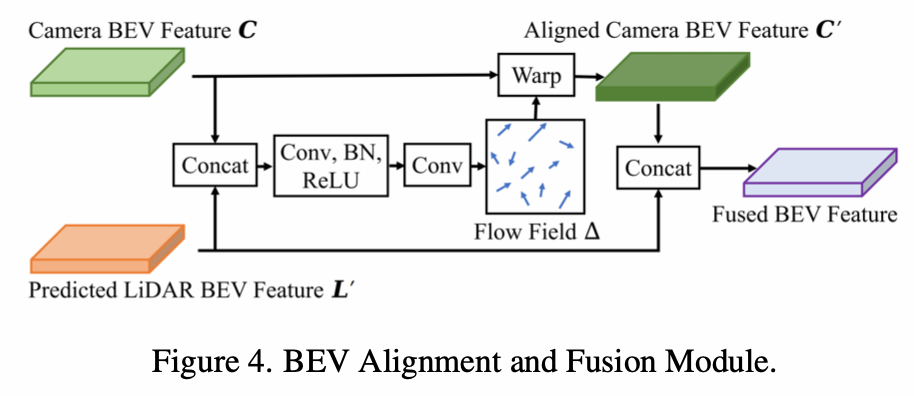
BEV层面的融合，将图像特征通过LSS转到BEV后，与点云BEV特征融合，但是由于内外参以及深度估计误差，所以直接concate会导致特征对不齐。所以它先concate然后学习一个flow field，根据据flow field对图像BEV特征进行重新计算(每个位置一个流动方向，然后双线性插值得到流动后的特征来作为当前图像BEV特征)，然后再将两者concate。

4.MachMap

相关文章：

在线高精地图生成算法调研

1.HDMapNet 整体的网络架构如图所示，最终的Decoder输出三个分支，一个语义分割，一个embedding嵌入分支，一个方向预测。然后通过后处理将这些信息处理成向量化的道路表示。 img2bev的方式之前有IPM，通过假设地面的高度都…...

编程日记 2023/8/9 4:31:54

【干货】商城系统的重要功能特性介绍

电子商务的快速发展，商城系统成为了企业开展线上销售的重要工具。一款功能强大、用户友好的商城系统能够有效提升企业的销售业绩，提供良好的购物体验。下面就商城系统的重要功能特性作一些简单介绍，帮助企业选择合适的系统，打造成…...

编程日记 2023/8/9 4:30:53

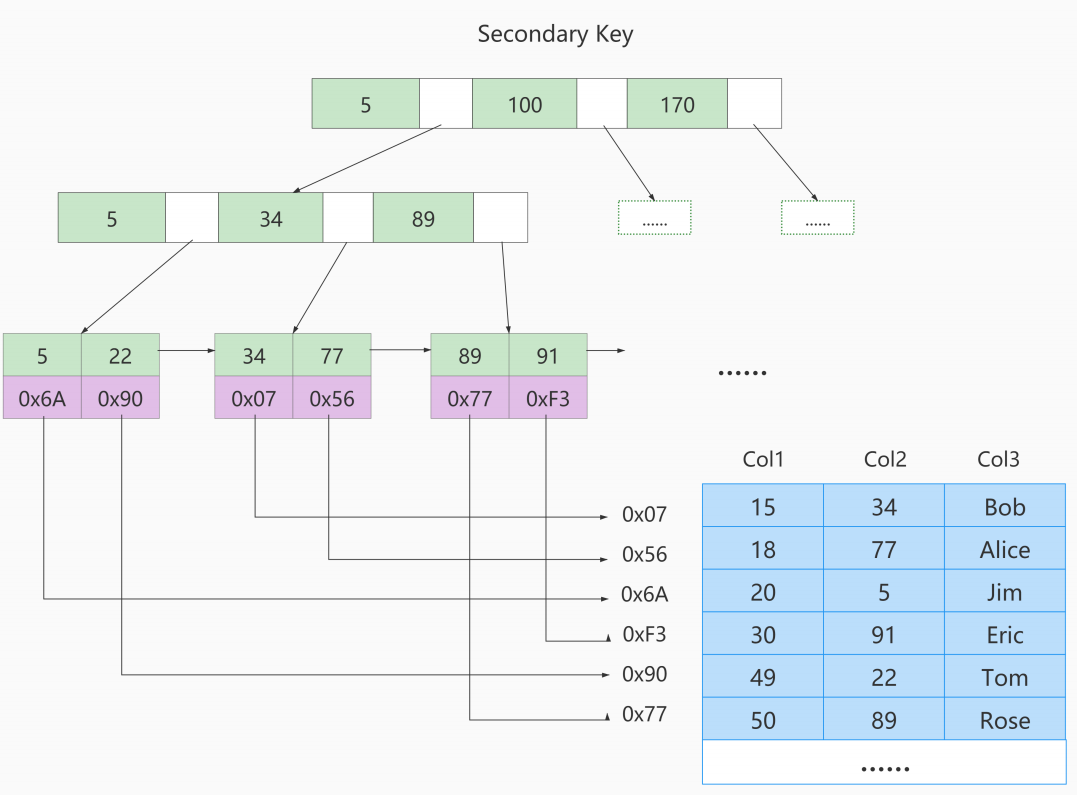
MYSQL06高级_为什么使用索引、优缺点、索引的设计、方案、聚簇索引、联合索引、注意事项

文章目录 ①. 为什么使用索引②. 索引及其优缺点③. InnoDb - 索引的设计④. InnoDb中的索引方案⑤. 索引 - 聚簇索引⑥. 索引 - 二级索引⑦. B树索引的注意事项⑧. MyISAM中索引方案 ①. 为什么使用索引 ①. 索引是存储引擎用于快速找到数据记录的一种数据结构,就好比去图书馆…...

编程日记 2023/8/9 4:29:51

LeetCode 130. 被围绕的区域

题目链接：130. 被围绕的区域 题目描述 给你一个 m x n 的矩阵 board ，由若干字符 ‘X’ 和 ‘O’ ，找到所有被 ‘X’ 围绕的区域，并将这些区域里所有的 ‘O’ 用 ‘X’ 填充。 示例1： 输入：board [[“…...

编程日记 2023/8/9 4:28:50

python中2等于2.0吗,python中【1:2】

本篇文章给大家谈谈python中2等于2.0吗，以及python中【1:2】，希望对各位有所帮助，不要忘了收藏本站喔。 变量和赋值 Python中的变量不需要声明, 直接定义即可. 会在初始化的时候决定变量的 “类型” 使用 来进行初始化和赋值操作 定义变量时…...

编程日记 2023/8/9 4:27:48

【2023年11月第四版教材】《第2章-信息技术发展（第一部分）》

《第2章-信息技术发展（第一部分）》 章节说明1 计算机软硬件2 计算机网络2.1 网络的作用范围2.2 OSI模型2.3 广域网协议2.4 网络协议2.5 TCP/IP2.6 软件定义网络（SDN）2.7 第五代移动通信技术 章节说明 大部分为新增内容&#xff0…...

编程日记 2023/8/9 4:26:48

【CSS】说说对BFC的理解

目录 一、概念 二、BFC的布局规则 三、设置BFC的常用方式 四、BFC的应用场景 1、解决浮动元素令父元素高度坍塌的问题 2、解决非浮动元素被浮动元素覆盖问题 3、解决外边距垂直方向重合的问题 五、总结 一、概念 我们在页面布局的时候，经常出现以下情况&am…...

编程日记 2023/8/9 4:25:47

ES6学习-Class类

class constructor 构造方法 this 代表实例对象 方法之间不需要逗号分隔，加了会报错。 typeof Point // "function" Point Point.prototype.constructor // true类的数据类型就是函数，类本身就指向构造函数。 类的所有方法都定义在类的pr…...

编程日记 2023/8/9 4:24:45

C语言经典小游戏之扫雷（超详解释+源码）

“少年气，是历尽千帆举重若轻的沉淀，也是乐观淡然笑对生活的豁达！” 今天我们学习一下扫雷游戏怎么用C语言来实现！ 扫雷小游戏 1.游戏介绍2.游戏准备3.游戏实现3.1生成菜单3.2游戏的具体实现3.2.1初始化棋盘3.2打印棋盘3.3布置雷…...

编程日记 2023/8/9 4:23:44

算法leetcode｜67. 二进制求和（rust重拳出击）

文章目录 67. 二进制求和：样例 1：样例 2：提示： 分析：题解：rust：go：c：python：java： 67. 二进制求和： 给你两个二进制字符串 a 和 b &a…...

编程日记 2023/8/9 4:22:44

【ASP.NET MVC】第一个登录页面（8）

一、准备工作 先从网上（站长之家、模板之家，甚至TB）下载一个HTML模板，要求一整套的CSS和必要的JS，比如下图： 登录页面的效果是： 首页： 利用这些模板可以减少前台网页的设计——拿来…...

编程日记 2023/8/9 4:21:43

使用Openoffice或LibreOffice实现World、Excel、PPTX在线预览

使用Openoffice或LibreOffice实现World、Excel、PPTX在线预览 预览方案使用第三方服务使用前端库转换格式 jodconverterjodconverter概述主要特性OpenOfficeLibreOffice jodconverter的基本使用添加依赖配置创建DocumentConverter实例上传与转换预览启动上传与预览World 与Spri…...

编程日记 2023/8/9 4:20:42

20天学会rust（三）没有object的rust怎么面向对象？

面向对象我们都很熟悉，可以说它是一种软件开发最重要的编程范式之一，它将程序中的数据和操作数据的方法组织成对象。面向对象有几个重要特性： 封装、继承和多态，基于这些特性带来了在可重用性、可维护性、扩展性、可靠性的优点。 …...

编程日记 2023/8/9 4:19:41

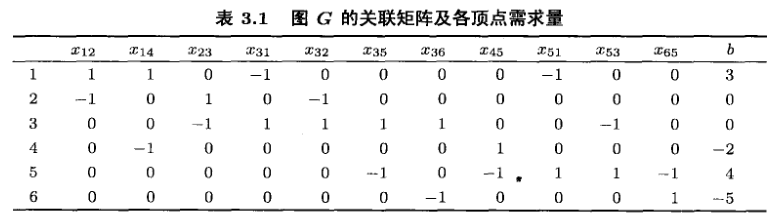
整数规划——第三章 全单模矩阵

整数规划——第三章 全单模矩阵 若线性规划问题的约束矩阵为全单模矩阵，则该问题可行域的顶点都是整数点，从而线性规划与整数规划的最优解相同。 3.1 全单模性与最优性 考虑线性整数规划问题： (IP) min ⁡ c T x , s . t . A x ≤ b , x …...

编程日记 2023/8/9 4:18:40

数据结构和算法

数据结构和算法目录表 CCJava线性结构 1. 数组、单链表和双链表 2. Linux内核中双向链表的经典实现 数组、单链表和双链表 数组、单链表和双链表 栈 栈 栈 队列 队列 队列树形结构 二叉查找树 二叉查找树 二叉查找树 AVL树 AVL树 AVL树 伸展树 伸展树 伸展树 1. 红黑树(一)之…...

编程日记 2023/8/9 4:17:39

[Vulnhub] matrix-breakout-2-morpheus

目录 <1> 信息收集 <2> getshell <3> Privilege Escalation&#xff08;提权&#xff09; <1> 信息收集 nmap -sP 192.168.236.0/24 扫描一下靶机ip 靶机ip: 192.168.236.154 nmap -A -p 1-65535 192.168.236.154 扫描一下靶机开放哪些服务 开放…...

编程日记 2023/8/9 4:16:37

JDK, JRE和JVM之间的区别和联系

JDK, JRE和JVM是与Java编程语言相关的三个重要的概念&#xff0c;它们分别代表Java Development Kit&#xff08;Java开发工具包&#xff09;、Java Runtime Environment&#xff08;Java运行时环境&#xff09;和Java虚拟机&#xff08;Java Virtual Machine&#xff09;。它们…...

编程日记 2023/8/9 4:15:36

mac电脑访问windows共享文件夹连接不上（设置445端口）

前提&#xff1a;首先需要保证mac和windows都在同一局域网内&#xff0c;如果不在肯定是连不上的&#xff0c;就不用往下看了。 事情是这样的&#xff0c;公司入职发了mac电脑&#xff0c;但是我是window重度用户&#xff0c;在折腾mac的过程中&#xff0c;有许多文件需要从wi…...

编程日记 2023/8/9 4:14:36

metersphere性能压测执行过程

(1) 首先在controller层&#xff0c;通过RunTestPlanRequest接收请求参数 PostMapping("/run")public String run(RequestBody RunTestPlanRequest request) (2) 在PerformanceTestService中的run中进行具体的逻辑处理&#xff0c; 首先根据请求中ID来获取库中存储…...

编程日记 2023/8/9 4:13:30

揭秘Word高级技巧：事半功倍的文字处理策略

Microsoft Word是一款广泛使用的文字处理软件&#xff0c;几乎每个人都有使用过它的经历。但是&#xff0c;你是否知道Word中隐藏着许多高级技巧和功能&#xff0c;可以帮助你事半功倍地处理文字&#xff1f;在本文中&#xff0c;我们将揭秘一些Word的高级技巧&#xff0c;让你…...

编程日记 2023/8/9 4:12:27

Science重磅指南：如何打造高影响力论文摘要？附Abstract写作黄金法则！

1. 科学论文摘要的黄金结构 写论文摘要就像给陌生人讲一个精彩的故事——要在短短200字内让人眼前一亮。我在Nature和Science上发过几篇论文&#xff0c;也审过上百篇投稿&#xff0c;发现顶级期刊的摘要其实有套"万能公式"。这个公式的核心是把摘要拆解成7个关键部分…...

编程新知 2026/3/27 5:24:45

dfs：飞机降落

题目&#xff1a;P9241 [蓝桥杯 2023 省 B] 飞机降落 - 洛谷 做题目之前一定要先看数据范围。这道题的数据范围&#xff0c;T,N均<10&#xff0c;可以用暴力搜索。 这道题是排序&#xff0c;假设有3辆飞机。顺序可以是123&#xff0c;132&#xff0c;213&#xff0c;231&am…...

编程新知 2026/3/27 5:24:45

异步AI流式响应总出错？FastAPI 2.0架构设计图首次公开：EventSource vs Server-Sent Events vs WebSockets选型决策树

第一章&#xff1a;FastAPI 2.0异步AI流式响应架构设计图全景概览FastAPI 2.0 引入了原生增强的异步流式响应支持&#xff0c;为大语言模型&#xff08;LLM&#xff09;推理、实时语音转写、多模态生成等AI场景提供了低延迟、高吞吐的基础设施能力。其核心在于将 ASGI 生命周期…...

编程新知 2026/3/27 5:08:43

革新性PDF打印解决方案：PDFtoPrinter全场景应用指南

革新性PDF打印解决方案&#xff1a;PDFtoPrinter全场景应用指南 【免费下载链接】PDFtoPrinter .Net Wrapper over PDFtoPrinter util allows to print PDF files. 项目地址: https://gitcode.com/gh_mirrors/pd/PDFtoPrinter 价值定位&#xff1a;重新定义PDF打印体验…...

编程新知 2026/3/27 4:46:02

Mojo+Python混合项目部署失败全记录（含完整错误日志溯源与跨运行时调试手册）

第一章&#xff1a;MojoPython混合项目部署失败全记录&#xff08;含完整错误日志溯源与跨运行时调试手册&#xff09;在将 Mojo 模块嵌入 Python 3.11 环境的 CI/CD 流水线中&#xff0c;首次构建即触发运行时崩溃。核心现象为 mojo_runtime_init() 在 Python 进程内调用后立即…...

编程新知 2026/3/27 4:23:50

手把手教你用PHPStudy部署彩虹云商城二开版（2025修复完整版，含自动对接与漏洞修复）

零基础实战&#xff1a;PHPStudy环境下的彩虹云商城完整部署指南&#xff08;2025安全强化版&#xff09; 在个人站长和电商创业者的圈子里&#xff0c;彩虹云商城系统一直以其轻量化和易用性备受青睐。最近接触到的这个2025修复版&#xff0c;不仅保留了原系统的核心优势&…...

编程新知 2026/3/27 4:07:40

百度网盘提速全攻略：从限速对抗到效能优化的实战指南

百度网盘提速全攻略&#xff1a;从限速对抗到效能优化的实战指南 【免费下载链接】baidu-wangpan-parse 获取百度网盘分享文件的下载地址 项目地址: https://gitcode.com/gh_mirrors/ba/baidu-wangpan-parse 诊断限速瓶颈&#xff1a;从协议层破解速度封印 原理图解&am…...

编程新知 2026/3/27 4:05:39

大一大二最容易忽视的一张“证书”，却悄悄决定了很多人的未来

很多大学生到了大三才突然发现一件事&#xff1a;有些机会&#xff0c;原来早在大一大二就已经埋好了门槛。比如——英语四六级。保研、考研复试、国企网申、研究生免修英语、甚至一些实习岗位筛选&#xff0c;很多时候都会看到同一行字&#xff1a;CET-4 / CET-6 成绩这张证书…...

编程新知 2026/3/27 4:01:38

3大核心能力重新定义macOS炉石传说对战体验：HSTracker全方位辅助系统解析

3大核心能力重新定义macOS炉石传说对战体验&#xff1a;HSTracker全方位辅助系统解析 【免费下载链接】HSTracker A deck tracker and deck manager for Hearthstone on macOS 项目地址: https://gitcode.com/gh_mirrors/hs/HSTracker HSTracker是一款专为macOS平台设计…...

编程新知 2026/3/27 3:35:08

const 变量的存储位置

const 变量的存储位置&#xff1a;不是绝对的只读区&#xff01;这是 C/C 面试/学习高频易错点&#xff0c;核心结论&#xff1a;const 只修饰「只读权限」&#xff0c;不直接决定存储位置&#xff0c;变量放哪里&#xff0c;由变量的「作用域/生命周期」决定。一、分情况讲清楚…...

编程新知 2026/3/27 2:56:48