PHP8定义字符串的方法-PHP8知识详解
字符串,顾名思义,就是将一堆字符串联在一起。字符串简单的定义方法是使用英文单引号(' ')或英文双引号(" ")包含字符。另外,还可以使用定界符定义字符串。本文还介绍了字符串的连接符。

一、使用单引号或双引号定义字符串
字符串是指一连串不中断的字符。这里的字符主要包括以下几种类型。
1.1、字母类型,如a、b、c、d等。
1.2、数字类型,如1、2、3、4等。
1.3、特殊字符型,如!、@、#、¥、%、&等。
1.4、不可见字符型,如回车符、tab符、换行符等。
下面所有单引号和双引号,来定义一个普通字符,并注意单双号的区别:
<?PHP
$a = "PHP8"; //定义变量$a,使用双引号定义
$b = 'PHP8'; //定义变量$b,使用单引号定义
$c = "我们正在学习的是$a"; //定义变量$c,使用双引号定义
$d = '我们正在学习的是$a'; //定义变量$d,使用单引号定义
echo $a; //输出变量$a
echo "<br>"; //输出换行
echo $b; //输出变量$b
echo "<br>"; //输出换行
echo $c; //输出变量$c
echo "<br>"; //输出换行
echo $d; //输出变量$d
?>
以上PHP8代码执行结果为:
PHP8
PHP8
我们正在学习的是PHP8
我们正在学习的是$a
从以上的运行结果可以得出:
1、仅仅输出字符串的时候,双引号和单引号是没有区别的。
2、当在字符串中输出变量的时候,就不一样了,双引号会输出变量的值,单引号则把变量当成普通的字符串原封不动的输出。
二、使用定界符定义字符串
定界符(<<<)用于定义格式化的大文本,这里的格式化是指文本中的格式被保留,所以文本中不需要转义字符。使用定界符的语法格式如下:
<?php
$string = <<< str
字符串的具体内容
str;
?>这里的str为指定的标识符,标识符可以自己设定,记得要前后保持一致。
使用定界符和双引号一样,包含的变量也会替换成实际的值。
参考案例如下:
<?php
$a = "PHP8";
$b = "我们正在学习的是$a";
$c = <<< str
我们正在学习的是$a
str;
echo $b;
echo "<br>";
echo $c;
?>
上面代码在PHP8中,运行结果如下:
我们正在学习的是PHP8
我们正在学习的是PHP8
三、字符串的连接符
字符串的连接符使用非常的频繁,在前面的学习中,我们学习了使用英文的“.”(点号)来链接,还可以使用{}来连接字符串。
3.1、使用“.”连接字符串。
它可以连接两个字符串,也可以连接两个字符串变量,还可以连接字符串和字符串变量。
示范代码如下:
<?php
$a = "我们正在学习的是";
$b = "PHP8";
echo $a.$b;
?>
在PHP8中运行的结果如下:
我们正在学习的是PHP8
3.2、使用“{}”连接字符串。
在PHP编程中,{}也是我们经常使用的连接字符的语法,特别是在各种cms中,我们经常看见,某些变量就是使用{}来链接的,下面是一个使用{}连接字符串的示范:
<?php
$a = "PHP";
$b = "PHP8";
$c = "我是一名{$a}程序员,我正在学习的是{$b}";
echo $c;
?>
在PHP8中运行的结果为:
我是一名PHP程序员,我正在学习的是PHP8
到此为止,使用单引号或双引号定义字符串、使用定界符定义字符串和字符串的连接符就讲解完毕了。欢迎你学习《PHP8知识详解》系列教程的其他知识点。
相关文章:

PHP8定义字符串的方法-PHP8知识详解
字符串,顾名思义,就是将一堆字符串联在一起。字符串简单的定义方法是使用英文单引号( )或英文双引号(" ")包含字符。另外,还可以使用定界符定义字符串。本文还介绍了字符串的连接符。…...

分享21年电赛F题-智能送药小车-做题记录以及经验分享
这里写目录标题 前言一、赛题分析1、车型选择2、巡线1、OpenMv循迹2、灰度循迹 3、装载药品4、识别数字5、LED指示6、双车通信7、转向方案1、开环转向2、位置环速度环闭环串级转向3、MPU6050转向 二、调试经验分享1、循迹2、识别数字3、转向4、双车通信5、逻辑处理6、心态问题 …...

字符串统计-C语言/Java
描述 计算字符串中含有的不同字符的个数。字符在 ASCII 码范围内( 0~127 ,包括 0 和 127 ),换行表示结束符,不算在字符里。不在范围内的不作统计。多个相同的字符只计算一次。数据范围: 1≤n≤500 例如,对于字符串 ab…...

Styled-components,另一种css in js的方案
介绍 Styled-components是一种流行的CSS-in-JS库,它为React和React Native应用程序提供了一种优雅的方式来管理组件的样式。它的设计理念是将CSS样式与组件逻辑紧密绑定在一起,从而使样式在组件层级中作用更加清晰和可维护 使用 安装Styled-components…...
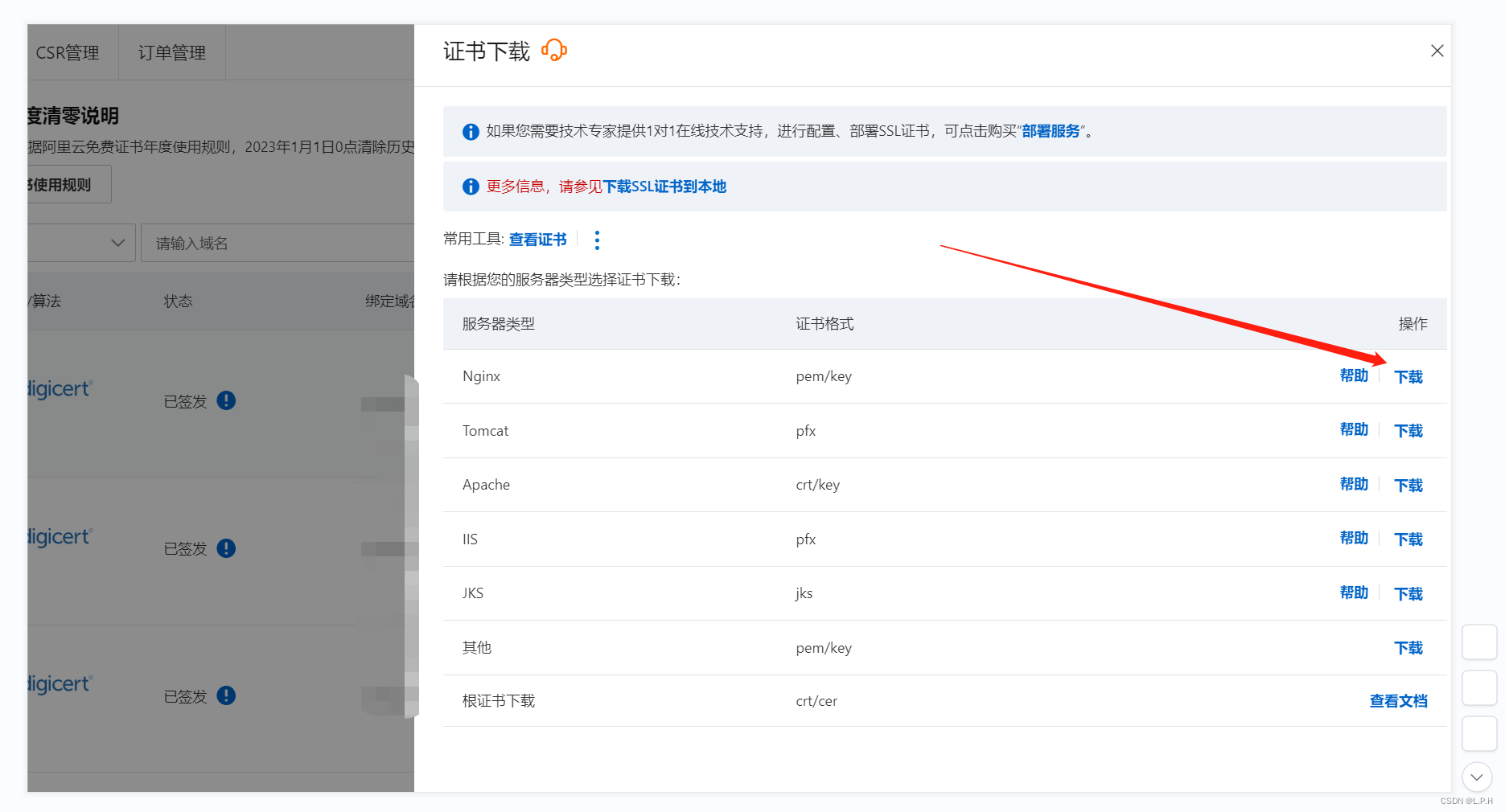
nginx部署以及反向代理多域名实现HTTPS访问
nginx部署以及反向代理多域名实现 1.nginx部署 1.1 编写nginx部署文件 docker-compose.yml version: 3 services: nginx:restart: always image: nginx:1.20container_name: nginx-mainports:- 80:80- 443:443volumes: # 基础配置- /opt/nginx_main/nginx-info/nginx.conf:/…...

24届近5年东华大学自动化考研院校分析
今天给大家带来的是东华大学控制考研分析 满满干货~还不快快点赞收藏 一、东华大学 学校简介 东华大学(Donghua University),地处上海市,是教育部直属全国重点大学,国家“双一流”、“211工程”建设高校…...

nacos伪集群启动成功,但是服务注册不上的问题
项目场景: nacos 伪集群启动成功,但是服务未注册上的问题: 问题描述 在学习nacos中,我买了一台阿里云服务器,在其上部署了nginx及三个nacos 端口分别是 8848 8868 8888 我按照正常的流程 解压nacos修改application.p…...
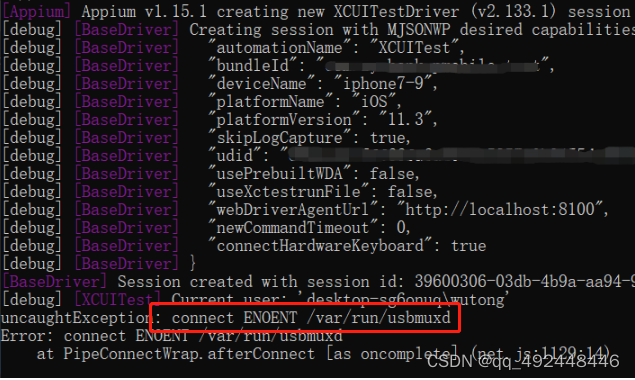
tidevice+appium在windows系统实施iOS自动化
之前使用iOS手机做UI自动化都是在Mac电脑上进行的,但是比较麻烦,后来看到由阿里开源的tidevice工具可以实现在windows上启动WDA,就准备试一下,记录一下过程。 tidevice的具体介绍可以参考一下这篇文章:tidevice 开源&…...
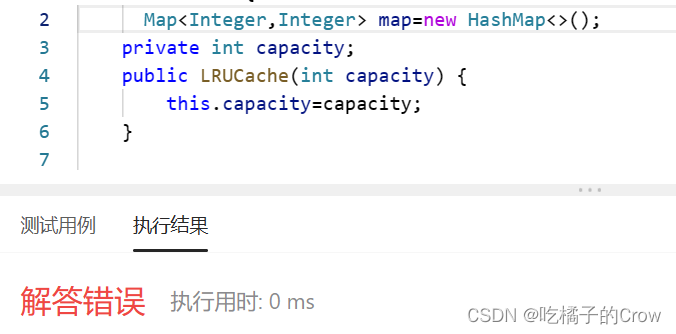
面试热题(LRU缓存)
请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。 实现 LRUCache 类: LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 …...
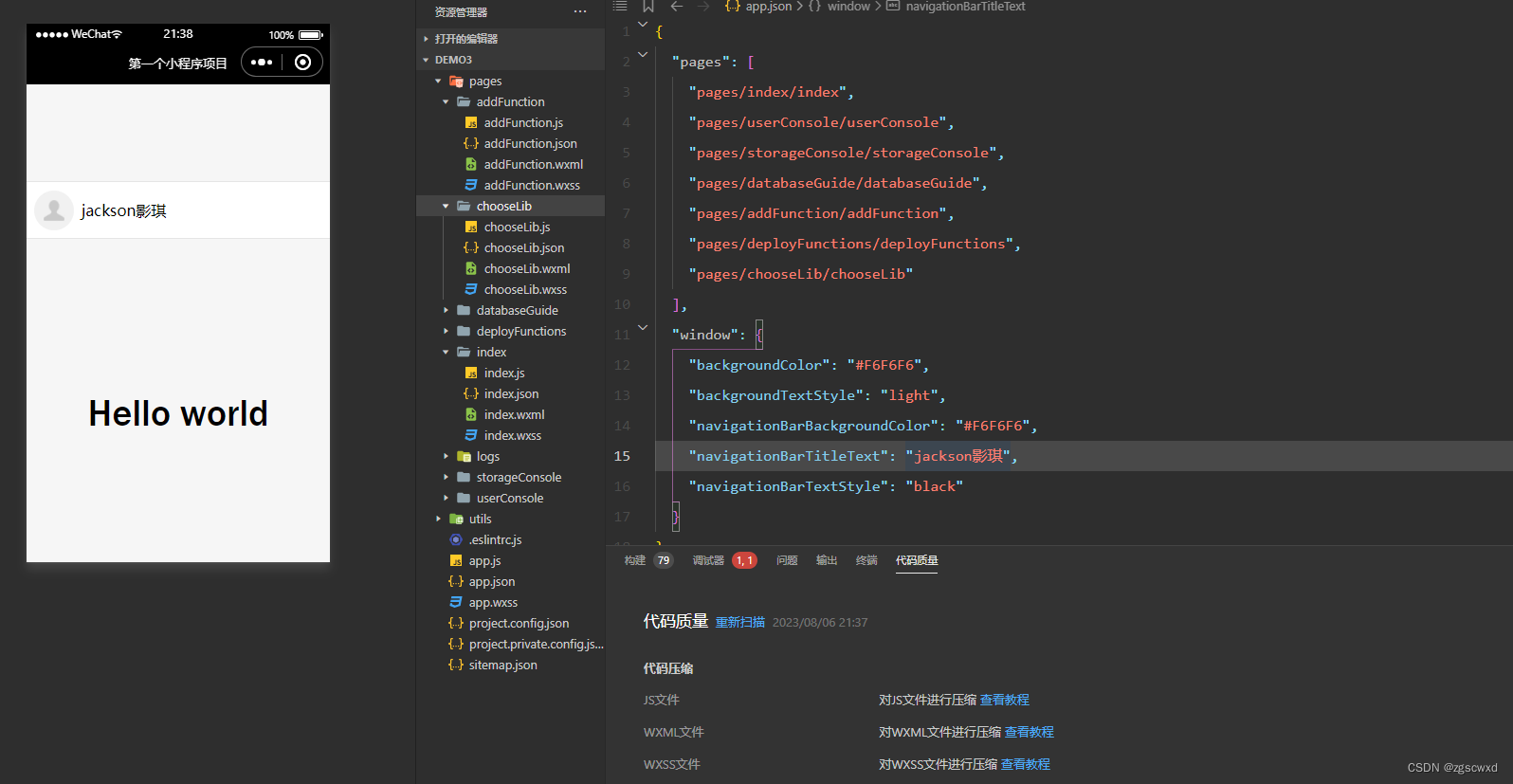
微信小程序开发【从0到1~入门篇】2023.08
一个小程序主体部分由三个文件组成,必须放在项目的根目录,如下: 文件必须作用app.js是小程序逻辑app.json是小程序公告配置app.wxss否小程序公告样式表 3. 小程序项目结构 一个小程序页面由四个文件组成,分别是: 文…...

P1398 [NOI2013] 书法家
题目描述 输入 #1 3 13 1 1 -1 -1 1 -1 1 1 1 -1 1 1 1 1 -1 1 -1 1 -1 1 -1 1 -1 -1 1 -1 1 -1 -1 1 1 -1 1 1 1 -1 1 1 1 输出 #1 24 输入 #2 3 13 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1…...
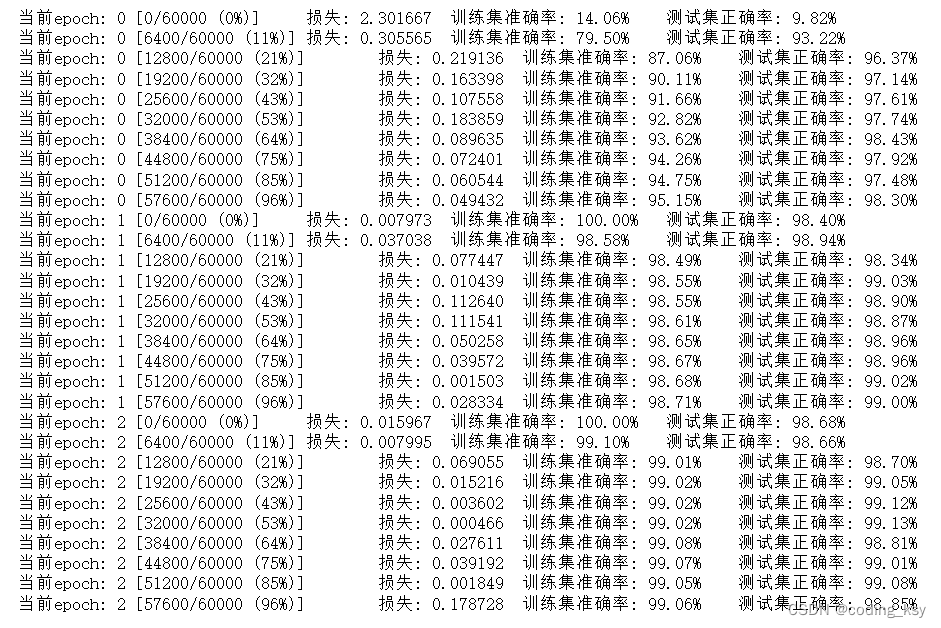
【构建卷积神经网络】
构建卷积神经网络 卷积网络中的输入和层与传统神经网络有些区别,需重新设计,训练模块基本一致 全连接层:batch784,各个像素点之间都是没有联系的。 卷积层:batch12828,各个像素点之间是有联系的。 impor…...

SSH 认证原理
SSH协议登录服务器: $ ssh userhost 主要有两种登录方式:第一种为密码口令登录,第二种为公钥登录 密码口令登录 通过密码进行登录,主要流程为: 1、客户端连接上服务器之后,服务器把自己的公钥传给客户端…...

基于DETR (DEtection TRansformer)开发构建MSTAR雷达影像目标检测系统
关于DETR相关的实践在之前的文章中很详细地介绍过,感兴趣的话可以自行移步阅读即可: 《DETR (DEtection TRansformer)基于自建数据集开发构建目标检测模型超详细教程》 《书接上文——DETR评估可视化》 基于MSTAR雷达影像数据开发构建目标检测系统&am…...

Java分布式微服务1——注册中心(Eureka/Nacos)
文章目录 基础知识注册中心Eureka注册中心与Ribbon负载均衡1、Eureka注册中心2、Eureka的搭建3、Eureka服务注册4、复制服务实例5、拉取服务6、Ribbon负载均衡的流程及Eureka规则调整:7、Ribbon负载均衡饥饿加载 Nacos注册中心1、服务端Nacos安装与启动2、客户端Nac…...

(文章复现)建筑集成光储系统规划运行综合优化方法matlab代码
参考文献: [1]陈柯蒙,肖曦,田培根等.一种建筑集成光储系统规划运行综合优化方法[J].中国电机工程学报,2023,43(13):5001-5012. 1.基本原理 本文建立的双层耦合模型内、外层分别对应求解容量配置与能量调度问题。外层模型设置光伏与储能容量备选集并将容量配置组合…...
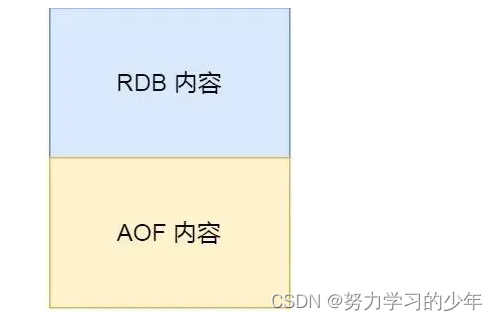
【Redis】——RDB快照
Redis 是内存数据库,但是它为数据的持久化提供了两个技术,一个是AOF日志,另一个是RDB快照: AOF 文件的内容是操作命令;RDB 文件的内容是二进制数据。 RDB 快照就是记录某一个瞬间的内存数据,记录的是实际…...
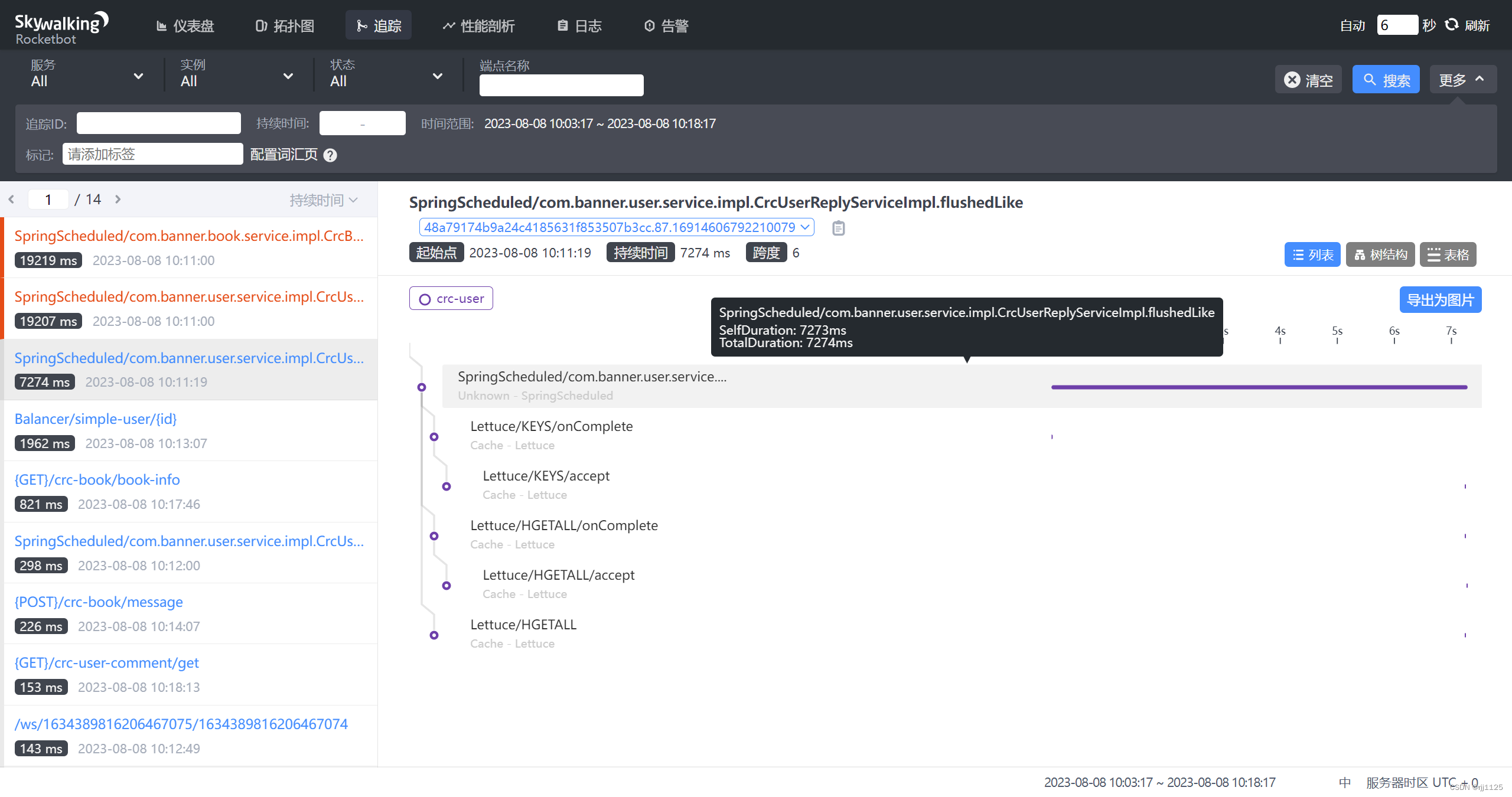
微服务监控技术skywalking的部署与使用(亲测无坑)
微服务监控技术skywalking的部署与使用 1. 前期准备2. skywalking安装部署2.1 Java Agent2.2 apache/skywalking-oap-server2.3 apache/skywalking-ui 3. 项目启动4.效果展示 1. 前期准备 注:本篇文章采用docker部署,采用8.2.0版本,版本一定…...
DLA 神经网络的极限训练方法:gradient checkpointing
gradient checkpointing 一般来说,训练的过程需要保存中间结果(不管是GPU还是CPU)。前向传播根据输入(bottom_data)计算输出(top_data),后向传播由top_diff计算bottom_diff(如果某个变量打开梯度进行训练的话ÿ…...

python excel 操作
excel文件内容如下: 一、xlrd 读Excel 操作 1、打开Excel文件读取数据 filexlrd.open_workbook(filename)#文件名以及路径,如果路径或者文件名有中文给前面加一个 r 2、常用函数 (1)获取一个sheet工作表 table file.sheets(…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...
