P1398 [NOI2013] 书法家
题目描述 

输入 #1
3 13
1 1 -1 -1 1 -1 1 1 1 -1 1 1 1
1 -1 1 -1 1 -1 1 -1 1 -1 -1 1 -1
1 -1 -1 1 1 -1 1 1 1 -1 1 1 1 输出 #1
24输入 #2
3 13
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1输出 #2
-20 
解析与代码







#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
#define MAXN 150
#define MAXM 500
#define INF 0x3fffffff
int a[MAXN+10][MAXM+10],n,m,blk[MAXM+10][2],f[2][10][MAXN+10][MAXN+10],s[MAXN+10][MAXM+10],tmp[MAXN+10][MAXN+10],ans=-INF;
void Read(int &x){static char c;bool f(0);while(c=getchar(),c!=EOF){if(c=='-')f=1;else if(c>='0'&&c<='9'){x=c-'0';while(c=getchar(),c>='0'&&c<='9')x=x*10+c-'0';ungetc(c,stdin);if(f)x=-x;return;}}
}
void read(){Read(n),Read(m);int i,j;for(i=1;i<=n;i++)for(j=1;j<=m;j++){Read(a[i][j]);s[i][j]=s[i-1][j]+a[i][j];}
}
void dp(){int i,j,k;memset(f[1],0xb0,sizeof f[1]);for(i=1;i<=n;i++)for(j=i;j<=n;j++)f[1][1][i][j]=s[j][1]-s[i-1][1];blk[1][0]=blk[1][1]=-INF;for(k=2;k<=m;k++){memset(f[k&1],0xb0,sizeof f[k&1]);//N的第一部分for(i=1;i<=n;i++)for(j=i;j<=n;j++)f[k&1][1][i][j]=max(s[j][k]-s[i-1][k],f[(k&1)^1][1][i][j]+s[j][k]-s[i-1][k]);//N的第二部分for(i=1;i<=n;i++){tmp[i][n+1]=-INF;for(j=n;j>=i;j--)tmp[i][j]=max(tmp[i][j+1],f[(k&1)^1][1][i][j]);}for(i=1;i<=n;i++)for(j=i;j<=n;j++){f[k&1][2][i][j]=max(f[k&1][2][i][j],tmp[i][j+1]+s[j][k]-s[i-1][k]);tmp[i][j]=-INF;}for(i=1;i<=n;i++)for(j=i;j<=n;j++)tmp[j+1][j+1]=max(tmp[j+1][j+1],f[(k&1)^1][2][i][j]);for(i=1;i<=n;i++)for(j=i+1;j<=n;j++)tmp[i][j]=max(tmp[i][j],tmp[i][j-1]);for(i=1;i<=n;i++)for(j=i;j<=n;j++)f[k&1][2][i][j]=max(f[k&1][2][i][j],tmp[i][j]+s[j][k]-s[i-1][k]);for(i=1;i<=n;i++)for(j=i;j<=n;j++)tmp[i][j]=f[(k&1)^1][2][i][j];for(j=1;j<=n;j++)for(i=1;i<j;i++)tmp[i+1][j]=max(tmp[i+1][j],tmp[i][j]);for(i=1;i<=n;i++)for(j=i;j<n;j++)tmp[i][j+1]=max(tmp[i][j+1],tmp[i][j]);for(i=1;i<=n;i++)for(j=i;j<=n;j++)f[k&1][2][i][j]=max(f[k&1][2][i][j],tmp[i][j]+s[j][k]-s[i-1][k]);//N的第三部分for(i=1;i<=n;i++)for(j=i;j<=n;j++)tmp[i][j]=f[(k&1)^1][2][i][j];for(j=1;j<=n;j++)for(i=j;i>1;i--)tmp[i-1][j]=max(tmp[i-1][j],tmp[i][j]);for(i=1;i<=n;i++)for(j=i+1;j<=n;j++)f[k&1][3][i][j]=max(f[k&1][3][i][j],max(tmp[i+1][j],f[(k&1)^1][3][i][j])+s[j][k]-s[i-1][k]);//NO之间空白blk[k][0]=blk[k-1][0];for(i=1;i<=n;i++)for(j=i;j<=n;j++)blk[k][0]=max(blk[k][0],f[(k&1)^1][3][i][j]);//O的第一部分for(i=1;i<=n;i++)for(j=i+2;j<=n;j++)f[k&1][4][i][j]=blk[k-1][0]+s[j][k]-s[i-1][k];//O的第二部分for(i=1;i<=n;i++)for(j=i+2;j<=n;j++)f[k&1][5][i][j]=max(f[(k&1)^1][4][i][j],f[(k&1)^1][5][i][j])+a[i][k]+a[j][k];//O的第三部分for(i=1;i<=n;i++)for(j=i+2;j<=n;j++)f[k&1][6][i][j]=f[(k&1)^1][5][i][j]+s[j][k]-s[i-1][k];//OI之间空白blk[k][1]=blk[k-1][1];for(i=1;i<=n;i++)for(j=i;j<=n;j++)blk[k][1]=max(blk[k][1],f[(k&1)^1][6][i][j]);//I的第一部分for(i=1;i<=n;i++)for(j=i+2;j<=n;j++)f[k&1][7][i][j]=max(blk[k-1][1],f[(k&1)^1][7][i][j])+a[i][k]+a[j][k];//I的第二部分for(i=1;i<=n;i++)for(j=i+2;j<=n;j++)f[k&1][8][i][j]=max(f[(k&1)^1][7][i][j],f[(k&1)^1][8][i][j])+s[j][k]-s[i-1][k];//I的第三部分for(i=1;i<=n;i++)for(j=i+2;j<=n;j++){f[k&1][9][i][j]=max(f[(k&1)^1][8][i][j],f[(k&1)^1][9][i][j])+a[i][k]+a[j][k];ans=max(ans,f[k&1][9][i][j]);} }
}
int main()
{read();dp();printf("%d\n",ans);
} 谢谢观看,希望对您有帮助![]()
相关文章:

P1398 [NOI2013] 书法家
题目描述 输入 #1 3 13 1 1 -1 -1 1 -1 1 1 1 -1 1 1 1 1 -1 1 -1 1 -1 1 -1 1 -1 -1 1 -1 1 -1 -1 1 1 -1 1 1 1 -1 1 1 1 输出 #1 24 输入 #2 3 13 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1…...
【构建卷积神经网络】
构建卷积神经网络 卷积网络中的输入和层与传统神经网络有些区别,需重新设计,训练模块基本一致 全连接层:batch784,各个像素点之间都是没有联系的。 卷积层:batch12828,各个像素点之间是有联系的。 impor…...

SSH 认证原理
SSH协议登录服务器: $ ssh userhost 主要有两种登录方式:第一种为密码口令登录,第二种为公钥登录 密码口令登录 通过密码进行登录,主要流程为: 1、客户端连接上服务器之后,服务器把自己的公钥传给客户端…...

基于DETR (DEtection TRansformer)开发构建MSTAR雷达影像目标检测系统
关于DETR相关的实践在之前的文章中很详细地介绍过,感兴趣的话可以自行移步阅读即可: 《DETR (DEtection TRansformer)基于自建数据集开发构建目标检测模型超详细教程》 《书接上文——DETR评估可视化》 基于MSTAR雷达影像数据开发构建目标检测系统&am…...

Java分布式微服务1——注册中心(Eureka/Nacos)
文章目录 基础知识注册中心Eureka注册中心与Ribbon负载均衡1、Eureka注册中心2、Eureka的搭建3、Eureka服务注册4、复制服务实例5、拉取服务6、Ribbon负载均衡的流程及Eureka规则调整:7、Ribbon负载均衡饥饿加载 Nacos注册中心1、服务端Nacos安装与启动2、客户端Nac…...

(文章复现)建筑集成光储系统规划运行综合优化方法matlab代码
参考文献: [1]陈柯蒙,肖曦,田培根等.一种建筑集成光储系统规划运行综合优化方法[J].中国电机工程学报,2023,43(13):5001-5012. 1.基本原理 本文建立的双层耦合模型内、外层分别对应求解容量配置与能量调度问题。外层模型设置光伏与储能容量备选集并将容量配置组合…...
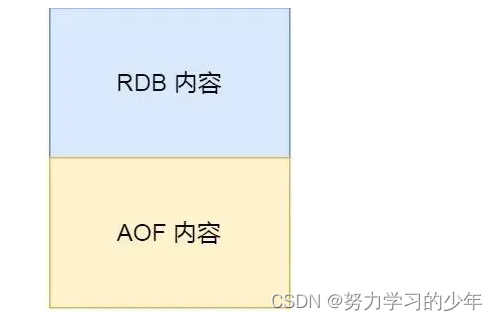
【Redis】——RDB快照
Redis 是内存数据库,但是它为数据的持久化提供了两个技术,一个是AOF日志,另一个是RDB快照: AOF 文件的内容是操作命令;RDB 文件的内容是二进制数据。 RDB 快照就是记录某一个瞬间的内存数据,记录的是实际…...
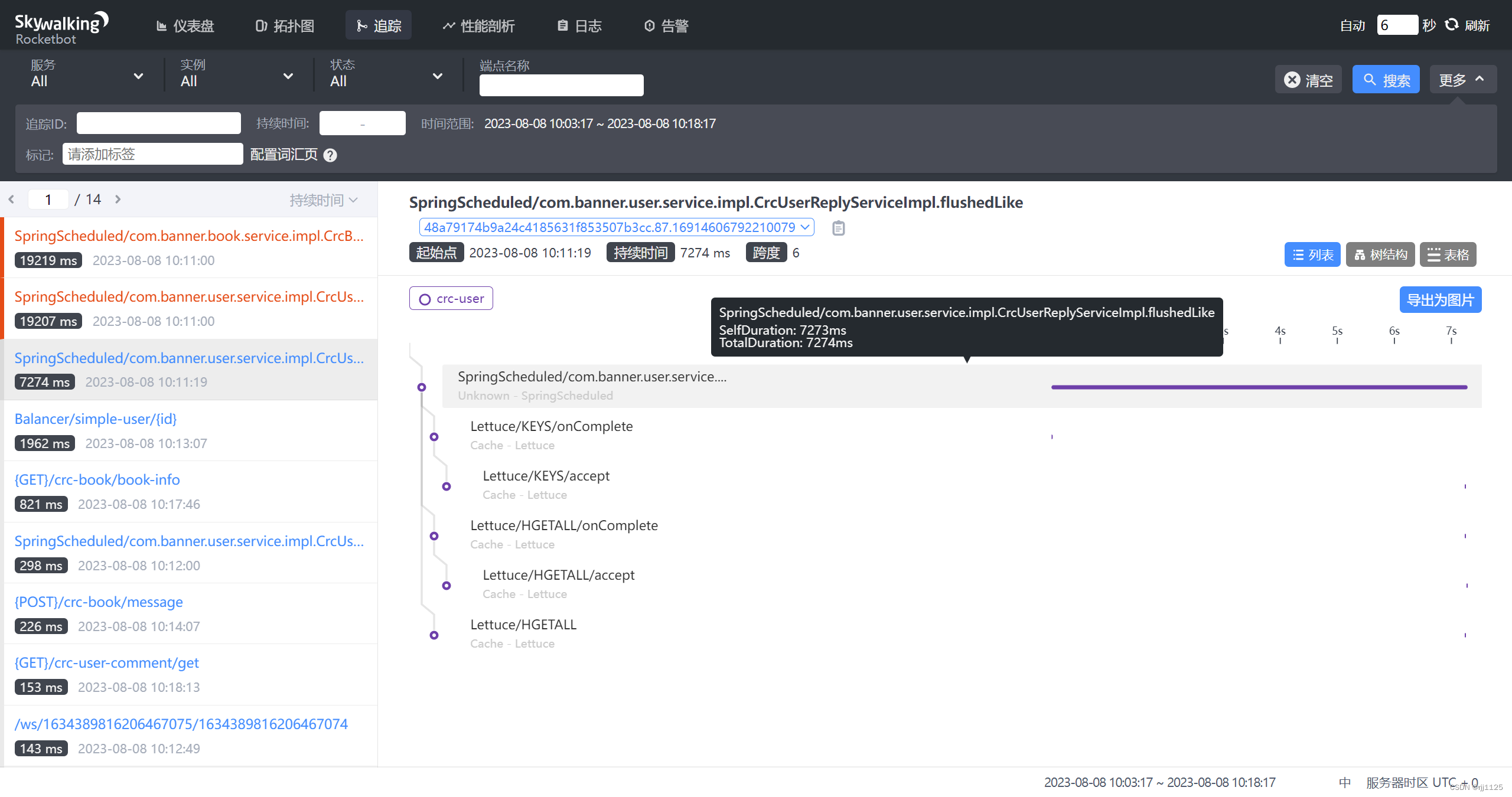
微服务监控技术skywalking的部署与使用(亲测无坑)
微服务监控技术skywalking的部署与使用 1. 前期准备2. skywalking安装部署2.1 Java Agent2.2 apache/skywalking-oap-server2.3 apache/skywalking-ui 3. 项目启动4.效果展示 1. 前期准备 注:本篇文章采用docker部署,采用8.2.0版本,版本一定…...
DLA 神经网络的极限训练方法:gradient checkpointing
gradient checkpointing 一般来说,训练的过程需要保存中间结果(不管是GPU还是CPU)。前向传播根据输入(bottom_data)计算输出(top_data),后向传播由top_diff计算bottom_diff(如果某个变量打开梯度进行训练的话ÿ…...

python excel 操作
excel文件内容如下: 一、xlrd 读Excel 操作 1、打开Excel文件读取数据 filexlrd.open_workbook(filename)#文件名以及路径,如果路径或者文件名有中文给前面加一个 r 2、常用函数 (1)获取一个sheet工作表 table file.sheets(…...

记一次Linux启动Mysql异常解决
文章目录 第一步: netstat -ntlp 查看端口情况2、启动Mysql3、查看MySQL日志 tail -100f /var/log/mysqld.log4、查看磁盘占用情况:df -h5、思路小结 第一步: netstat -ntlp 查看端口情况 并没有发现3306数据库端口 2、启动Mysql service …...
ATFX汇市:美联储年内或仍将加息依次,美指向下空间不大
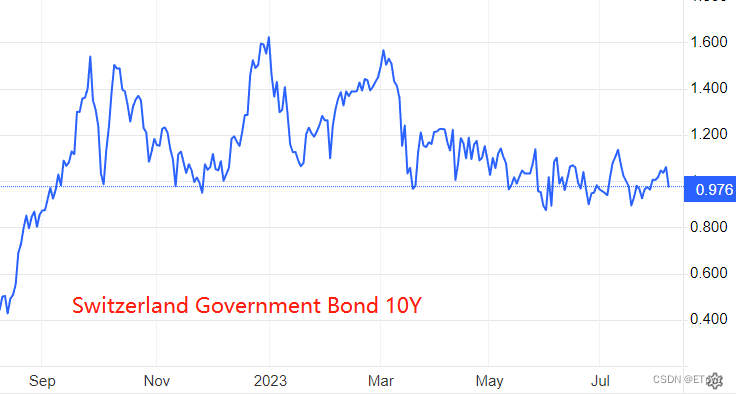
环球汇市行情摘要—— 昨日,美元指数上涨0.08%,收盘在102.08点, 欧元贬值0.07%,收盘价1.1003点; 日元贬值0.51%,收盘价142.47点; 英镑升值0.28%,收盘价1.2784点; 瑞…...

【博客687】k8s informer的list-watch机制剖析
k8s informer的list-watch机制剖析 1、list-watch场景: client-go中的reflector模块首先会list apiserver获取某个资源的全量信息,然后根据list到的rv来watch资源的增量信息。希望使用client-go编写的控制器组件在与apiserver发生连接异常时,…...
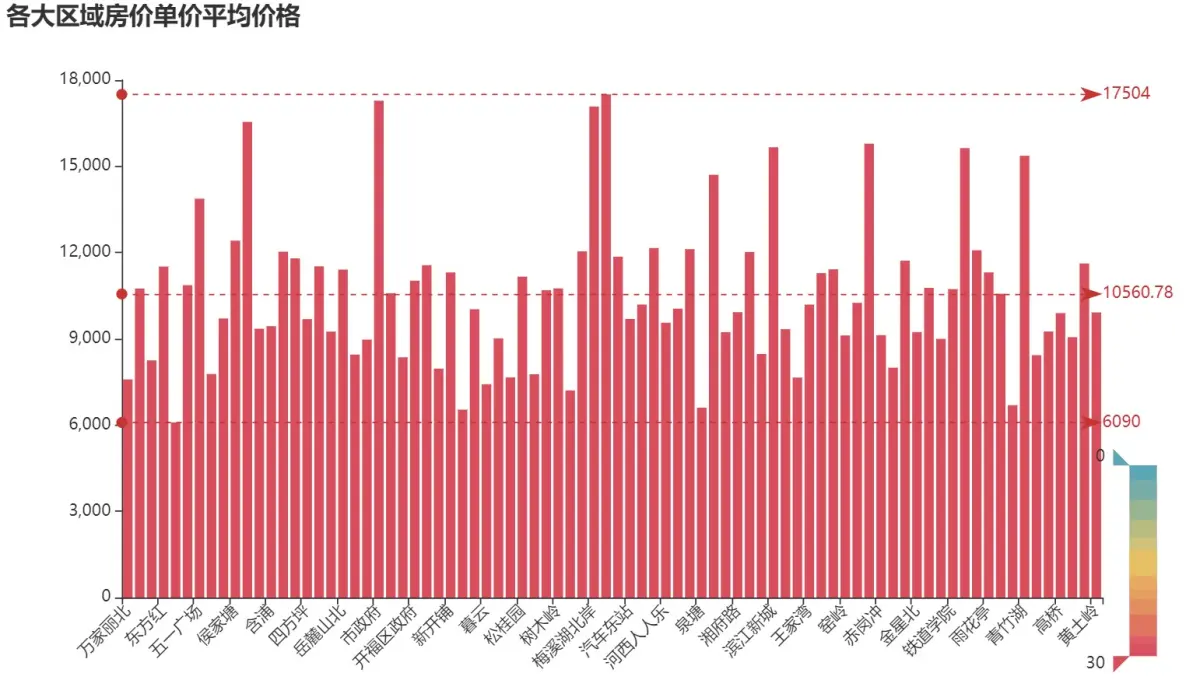
用Python获取链家二手房房源数据,做可视化图分析数据
前言 数据采集的步骤是固定: 发送请求, 模拟浏览器对于url地址发送请求获取数据, 获取网页数据内容 --> 请求那个链接地址, 返回服务器响应数据解析数据, 提取我们需要的数据内容保存数据, 保存本地文件 所需模块 win R 输入cmd 输入安装命令 pip install 模块名 (如果你…...

Yield Guild Games:社区更新 — 2023 年第二季度
本文重点介绍了 Yield Guild Games (YGG) 2023 年第二季度社区更新中涵盖的关键主题,包括公会发展计划 (GAP) 第 3 季的总结、YGG 领导团队的新成员以及 YGG 的最新消息地区公会网络和广泛的游戏合作伙伴生态系统。 在 YGG 品牌焕然一新的基础上,第二季…...

Stable Diffusion - 运动服 (Gymwear Leggings) 风格服装与背景的 LoRA 配置
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://spike.blog.csdn.net/article/details/132179050 测试模型:DreamShaper 8 运动裤 (Gymwear Leggings) 是紧身的裤子,通常用于健身、瑜伽、跑步等运动。运动裤的…...

js-7:javascript原型、原型链及其特点
1、原型 JavaScript常被描述为一种基于原型的语言-每个对象拥有一个原型对象。 当试图访问一个对象的属性时,它不仅仅在该对象上搜寻,还会搜寻该对象的原型,以及该对象的原型的原型,依次层层向上搜索,直到找到一个名字…...

无涯教程-Perl - continue 语句函数
可以在 while 和 foreach 循环中使用continue语句。 continue - 语法 带有 while 循环的 continue 语句的语法如下- while(condition) {statement(s); } continue {statement(s); } 具有 foreach 循环的 continue 语句的语法如下- foreach $a (listA) {statement(s); } co…...
【贪心算法】leetcode刷题
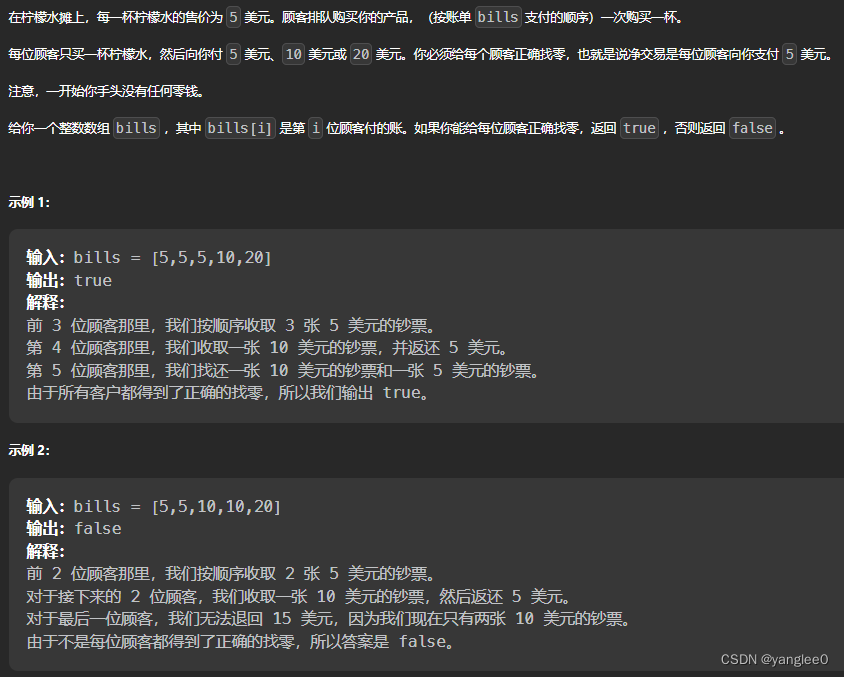
贪心算法无固定套路。 核心思想:先找局部最优,再扩展到全局最优。 455.分发饼干 两种思路: 1、从大到小。局部最优就是大饼干喂给胃口大的,充分利用饼干尺寸喂饱一个,全局最优就是喂饱尽可能多的小孩。先遍历的胃口&a…...

PyMySQL库版本引起的python执行sql编码错误
前言 长话短说,之前在A主机(centos7.9)上运行的py脚本拿到B主机上(centos7.9)运行报错: UnicodeEncodeError: latin-1 codec cant encode characters in position 265-266: ordinal not in range(256)两个…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...
