【贪心算法】leetcode刷题
贪心算法无固定套路。
核心思想:先找局部最优,再扩展到全局最优。
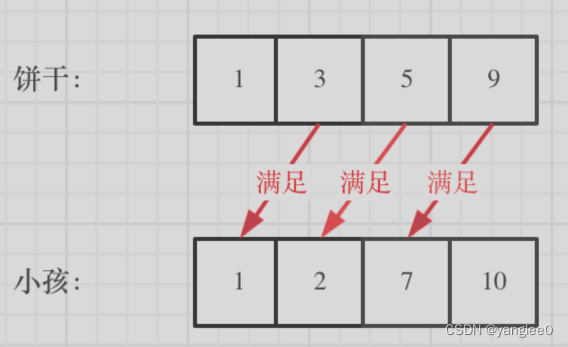
455.分发饼干

两种思路:
1、从大到小。局部最优就是大饼干喂给胃口大的,充分利用饼干尺寸喂饱一个,全局最优就是喂饱尽可能多的小孩。先遍历的胃口,在遍历的饼干
class Solution:def findContentChildren(self, g: List[int], s: List[int]) -> int:g = sorted(g,reverse=True)s = sorted(s,reverse=True)count = 0si = 0for gi in g:if si<len(s) and s[si]>=gi: # 饼干要大于胃的容量,才能喂饱count+=1si+=1 return count
2、从小到大。小饼干先喂饱小胃口。两个循环的顺序改变了,先遍历的饼干,在遍历的胃口,这是因为遍历顺序变了,我们是从小到大遍历。
class Solution:def findContentChildren(self, g: List[int], s: List[int]) -> int:g = sorted(g)s = sorted(s)count = 0gi = 0for si in s:if gi<len(g) and g[gi]<=si: # 胃的容量要小于等于饼干大小才能喂饱count+=1gi+=1 return count
376. 摆动序列

具体实例:
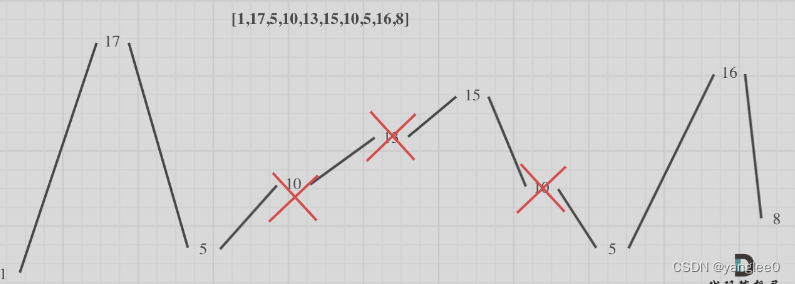
局部最优:删除单调坡度上的节点(不包括单调坡度两端的节点),那么这个坡度就可以有两个局部峰值。
**整体最优:**整个序列有最多的局部峰值,从而达到最长摆动序列。
考虑几种情况:
- 情况一:上下坡中有平坡
- 情况二:数组首尾两端
- 情况三:单调坡中有平坡
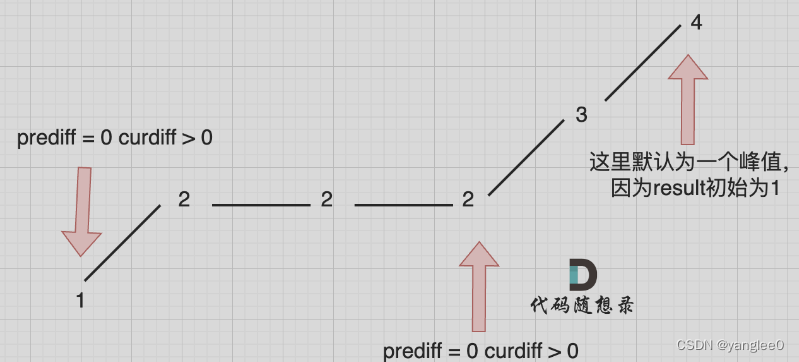
情况一:上下坡中有平坡
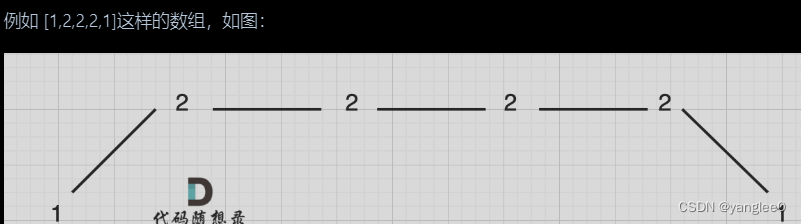
它的摇摆序列长度是多少呢? 其实是长度是 3,也就是我们在删除的时候 要不删除左面的三个 2,要不就删除右边的三个 2。
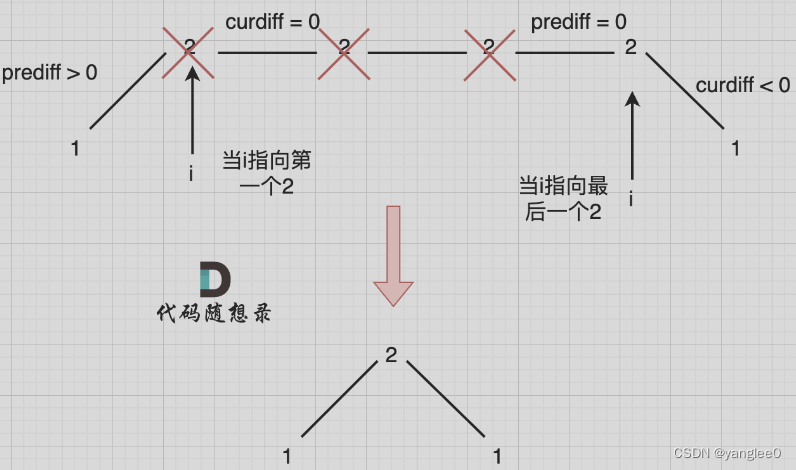
在图中,当 i 指向第一个 2 的时候,prediff > 0 && curdiff = 0 ,当 i 指向最后一个 2 的时候 prediff = 0 && curdiff < 0。
如果我们采用,删左面三个 2 的规则,那么 当 prediff = 0 && curdiff < 0 也要记录一个峰值,因为他是把之前相同的元素都删掉留下的峰值。
所以我们记录峰值的条件应该是: (preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0),为什么这里允许 prediff == 0 ,就是为了 上面我说的这种情况。
情况二:数组首尾两端
例如序列[2,5],如果靠统计差值来计算峰值个数就需要考虑数组最左面和最右面的特殊情况。
因为我们在计算 prediff(nums[i] - nums[i-1]) 和 curdiff(nums[i+1] - nums[i])的时候,至少需要三个数字才能计算,而数组只有两个数字。
这里我们可以写死,就是 如果只有两个元素,且元素不同,那么结果为 2。
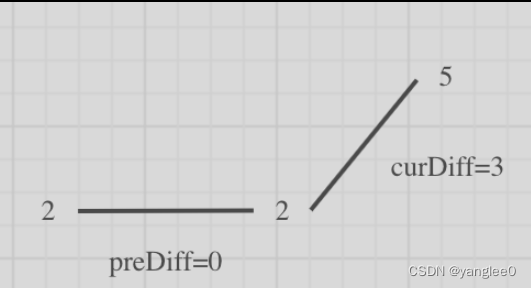
情况三:单调坡度有平坡
class Solution:def wiggleMaxLength(self, nums: List[int]) -> int:count = 1# 情况二,小于等于2的情况,可以写死if len(nums)<2:return len(nums)if len(nums)==2:if nums[-1]-nums[0]==0:return 1return len(nums)# 情况一以及情况三:prediff = 0for i in range(0,len(nums)-1):# if i>0:# prediff = nums[i-1]-nums[i]curdiff = nums[i]-nums[i+1]if (prediff<=0 and curdiff>0) or (prediff>=0 and curdiff<0):count+=1prediff = curdiff # 更新prediffreturn count
122.买卖股票的最佳时机 II

如果想到其实最终利润是可以分解的,那么本题就很容易了!
如何分解呢?
假如第 0 天买入,第 3 天卖出,那么利润为:prices[3] - prices[0]。
相当于==(prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0])==。
此时就是把利润分解为每天为单位的维度,而不是从 0 天到第 3 天整体去考虑!
那么根据 prices 可以得到每天的利润序列:(prices[i] - prices[i - 1])…(prices[1] - prices[0])。
- 局部最优:收集每天的正利润,全局最优:求得最大利润。
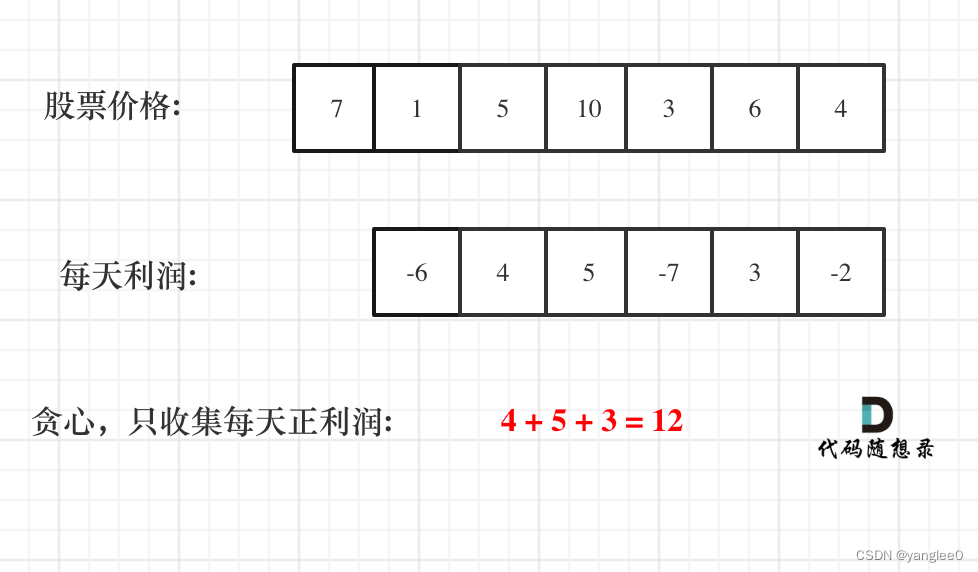
class Solution:def maxProfit(self, prices: List[int]) -> int:n = len(prices)dp = [0]*(n-1)for i in range(1,n):dp[i-1] = prices[i]-prices[i-1]res = 0for i in dp:if i>0:res+=ireturn res
55. 跳跃游戏

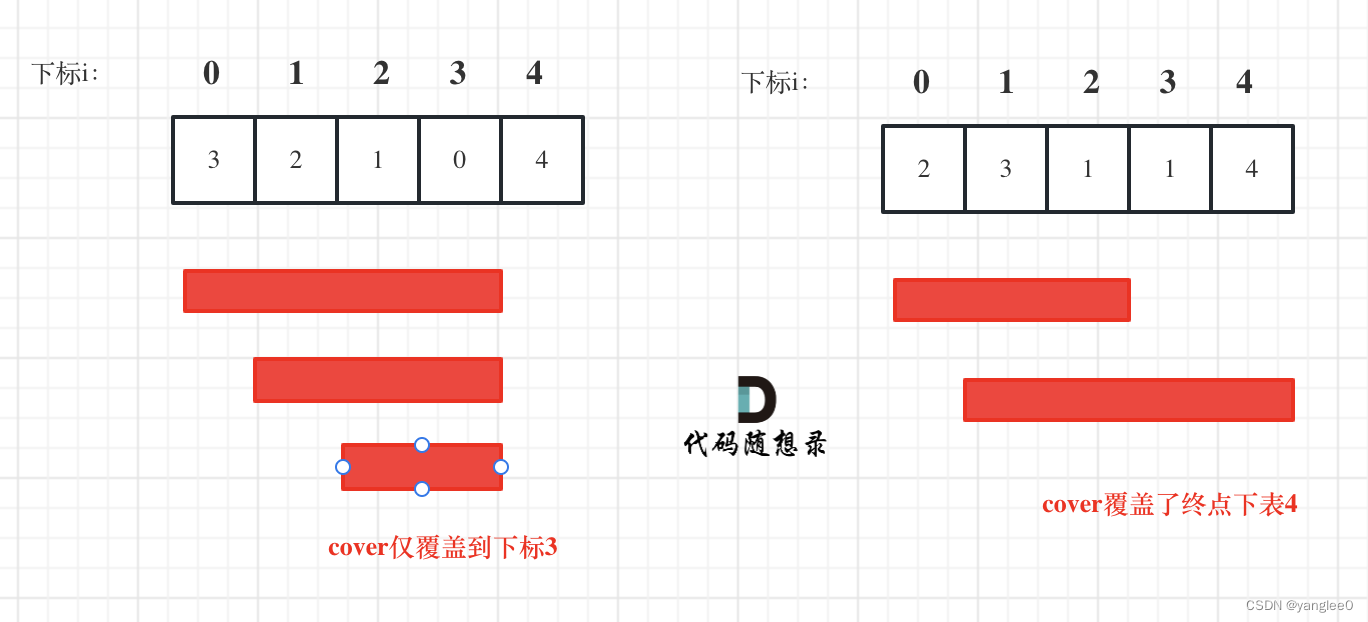
每次移动取最大跳跃步数(得到最大的覆盖范围),每移动一个单位,就更新最大覆盖范围。
贪心算法局部最优解:每次取最大跳跃步数(取最大覆盖范围),整体最优解:最后得到整体最大覆盖范围,看是否能到终点。
i 每次移动只能在 cover 的范围内移动,每移动一个元素,cover 得到该元素数值(新的覆盖范围)的补充,让 i 继续移动下去。
而 cover 每次只取 max(该元素数值补充后的范围, cover 本身范围)。
如果 cover 大于等于了终点下标,直接 return true 就可以了。
class Solution:def canJump(self, nums: List[int]) -> bool:n = len(nums)cover = 0if n<2:return Truefor i in range(n-1):if cover>=i:cover = max(cover,i+nums[i])if cover>=n-1:return Truereturn False
45.跳跃游戏 II

如果移动下标等于当前覆盖最大距离下标, 需要再走一步(即 ans++),因为最后一步一定是可以到的终点。(题目假设总是可以到达数组的最后一个位置),如图:
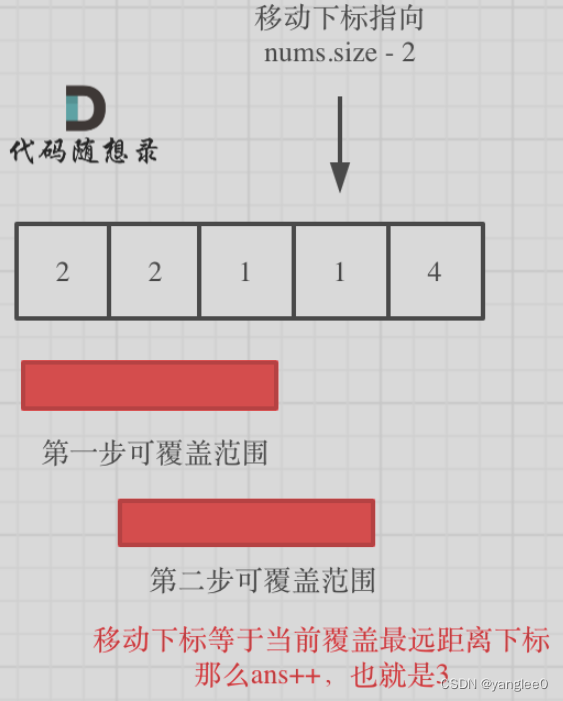
如果移动下标不等于当前覆盖最大距离下标,说明当前覆盖最远距离就可以直接达到终点了,不需要再走一步。如图:
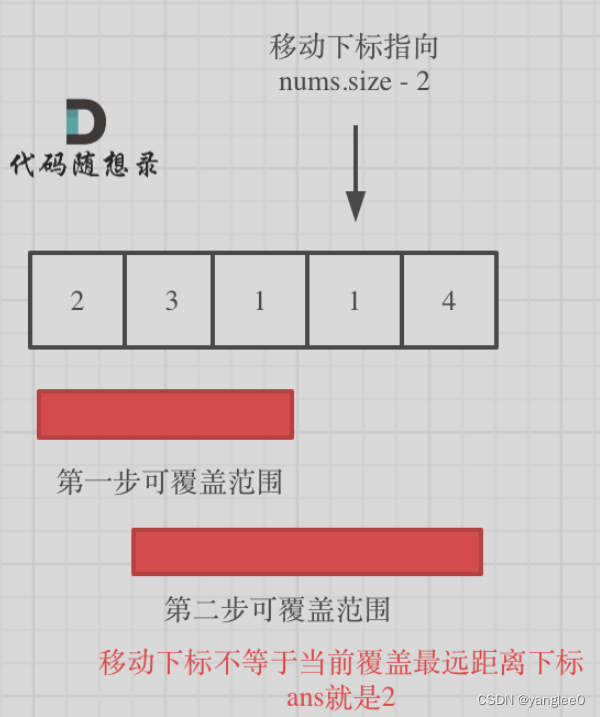
class Solution:def jump(self, nums: List[int]) -> int:cur_distance = 0 # 当前覆盖的最远距离下标ans = 0 # 记录走的最大步数next_distance = 0 # 下一步覆盖的最远距离下标for i in range(len(nums) - 1): # 注意这里是小于len(nums) - 1,这是关键所在next_distance = max(nums[i] + i, next_distance) # 更新下一步覆盖的最远距离下标if i == cur_distance: # 遇到当前覆盖的最远距离下标cur_distance = next_distance # 更新当前覆盖的最远距离下标ans += 1return ans1005.K次取反后最大化的数组和

class Solution:def largestSumAfterKNegations(self, nums: List[int], k: int) -> int:nums.sort(key=lambda x:abs(x),reverse=True) # 按照绝对值的个数排序,且从大到小,为了后面先将前k个大负数进行翻转为正数,保证和最大for i in range(len(nums)):if nums[i]<0 and k>0: # 将负数都翻转为正数k-=1nums[i] = -nums[i]# 现在全部都是正数了if k%2==1: # 如果还剩奇数个,则将最小的正数翻转nums[-1] = -nums[-1]# 如果是偶数,其实不用管,因为随便翻转个正数偶数次就可以了,不影响最后结果return sum(nums)
134. 加油站
135.分发糖果

- 从左到右:
如果ratings[i] > ratings[i - 1] 那么[i]的糖 一定要比[i - 1]的糖多一个,所以贪心:candyVec[i] = candyVec[i - 1] + 1
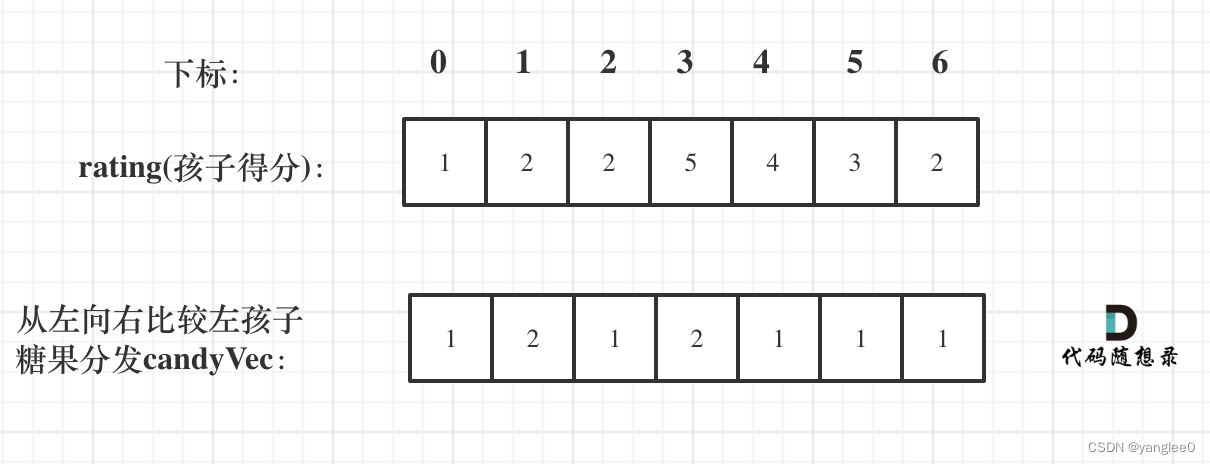
- 从右到左考虑:
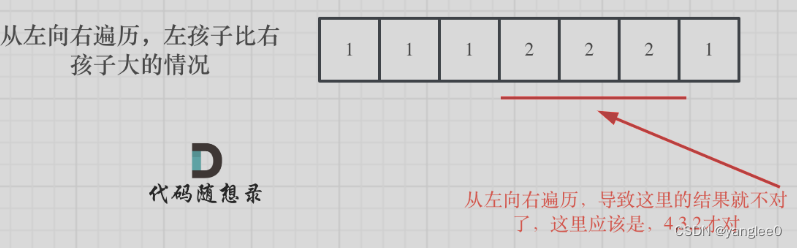
再确定左孩子大于右孩子的情况(从后向前遍历)
遍历顺序这里有同学可能会有疑问,为什么不能从前向后遍历呢?
因为 rating[5]与rating[4]的比较 要利用上 rating[5]与rating[6]的比较结果,所以 要从后向前遍历。
如果从前向后遍历,rating[5]与rating[4]的比较 就不能用上 rating[5]与rating[6]的比较结果了 。如图:
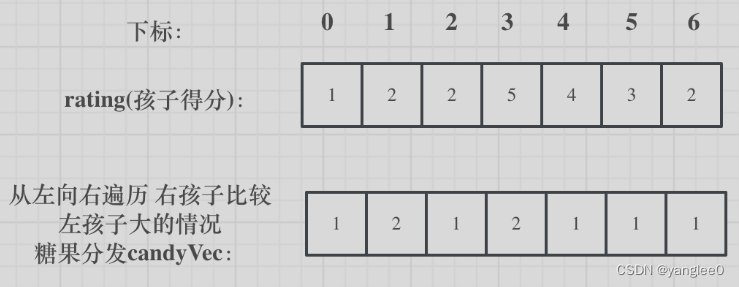
如果 ratings[i] > ratings[i + 1],此时candyVec[i](第i个小孩的糖果数量)就有两个选择了,一个是candyVec[i + 1] + 1(从右边这个加1得到的糖果数量),一个是candyVec[i](之前比较右孩子大于左孩子得到的糖果数量)。
那么又要贪心了,局部最优:取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量,保证第i个小孩的糖果数量既大于左边的也大于右边的。全局最优:相邻的孩子中,评分高的孩子获得更多的糖果。
所以就取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量,candyVec[i]只有取最大的才能既保持对左边candyVec[i - 1]的糖果多,也比右边candyVec[i + 1]的糖果多。
class Solution:def candy(self, ratings: List[int]) -> int:k = len(ratings)dp = [1]*k# 从左到右for i in range(k):if i>0 and ratings[i]>ratings[i-1]:dp[i] = dp[i-1]+1# 从右到左for i in range(k-2,-1,-1):if ratings[i]>ratings[i+1]:dp[i] = max(dp[i+1]+1,dp[i]) # 关键点 见解析return sum(dp)
860. 柠檬水找零
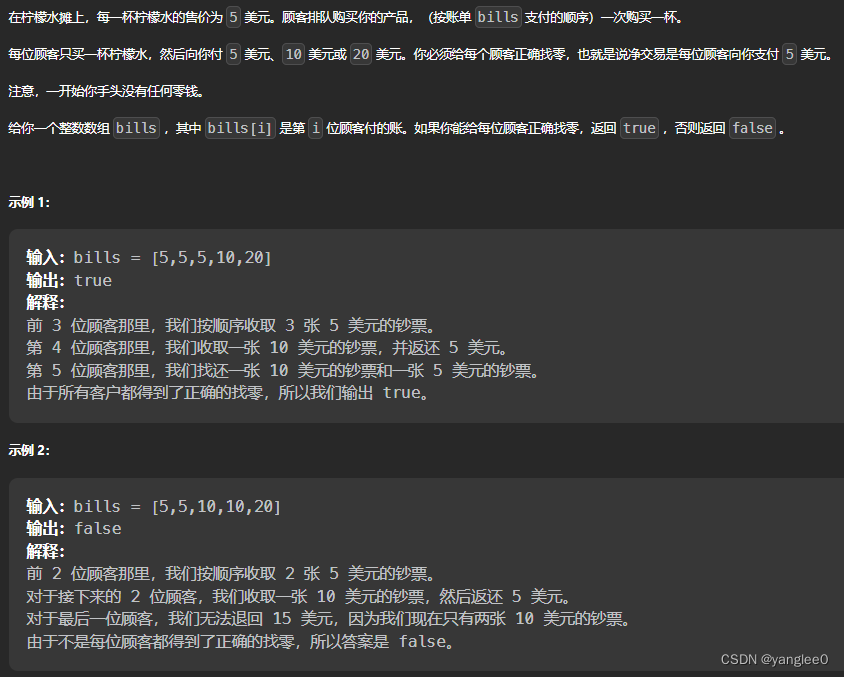
class Solution:def lemonadeChange(self, bills: List[int]) -> bool:if bills[0] != 5:return Falsen = len(bills)counter = {5: 0}for i in range(n):remain = bills[i]# 添加if remain in counter.keys():counter[remain] += 1else:counter[remain] = 1# 删除 # 若有20的,先找10元的。if remain // 10 > 1 and 10 in counter.keys():if counter[10] >= (remain // 10) - 1: # 先找10元的。counter[10] = counter[10] - ((remain // 10) - 1)remain = ((remain // 10) - 1) * 10# 删除 若是10/20,则进行删除操作if remain // 5 > 1:if counter[5] >= (remain // 5) - 1: # 再找5元的。剩余的5个数,大于需要找回的。counter[5] = counter[5] - ((remain // 5) - 1)else:return Falsereturn True
相关文章:

【贪心算法】leetcode刷题
贪心算法无固定套路。 核心思想:先找局部最优,再扩展到全局最优。 455.分发饼干 两种思路: 1、从大到小。局部最优就是大饼干喂给胃口大的,充分利用饼干尺寸喂饱一个,全局最优就是喂饱尽可能多的小孩。先遍历的胃口&a…...

PyMySQL库版本引起的python执行sql编码错误
前言 长话短说,之前在A主机(centos7.9)上运行的py脚本拿到B主机上(centos7.9)运行报错: UnicodeEncodeError: latin-1 codec cant encode characters in position 265-266: ordinal not in range(256)两个…...

第二章-算法
第二章-算法 数据结构和算法的关系 算法是解决特定问题求解步骤的描述,在计算机中表现为指令的有限序列,并且每条指令表示一个或多个操作。 算法的特性 算法有五个基本特征:输入、输出、有穷性、确定性和可行性。 输入:算法具…...
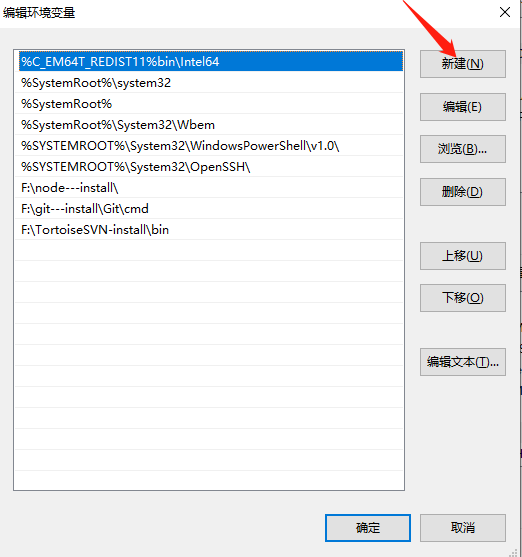
‘vue’不是内部或外部命令,也不是可运行的程序或批处理文件的原因及解决方法
今天我在用node.js的时候,结果出现如下错误: C:\Users\xiesj> vue -v vue不是内部或外部命令,也不是可运行的程序或批处理文件。 原因: 1、确定npm是否已正确安装? 2、确定vue以及vue-cli已正确安装?…...
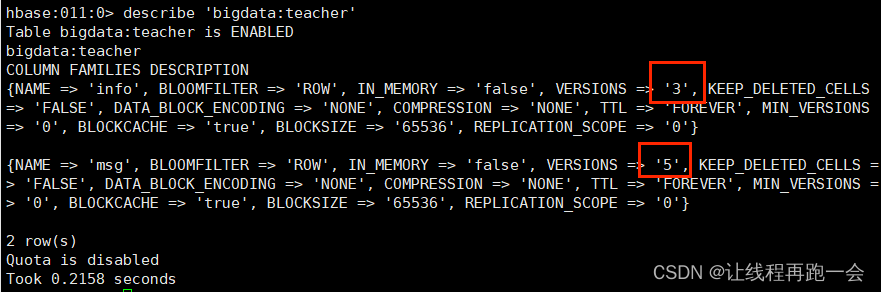
HBase API
我们之后的实际开发中不可能在服务器那边直接使用shell命令一直敲的,一般都是通过API进行操作的。 环境准备 新建Maven项目,导入Maven依赖 <dependencies><dependency><groupId>org.apache.hbase</groupId><artifactId>…...
Qt6之QListWidget——Qt仿ToDesk侧边栏(1)
一、 QLitWidget概述 注意:本文不是简单翻译Qt文档或者接口函数,而侧重于无代码Qt设计器下演示使用。 QListWidget也称列表框类,它提供了一个类似于QListView提供的列表视图,但是它具有一个用于添加和删除项的经典的基于项的接口…...
Prometheus技术文档--基本安装-docker安装并挂载数据卷-《十分钟搭建》
一、查看可安装的版本 docker search prom/prometheus 二、拉取镜像 docker pull prom/prometheus 三、查看镜像 docker images 四、书写配置文件-以及创建挂载目录 宿主机挂载目录位置: 以及准备对应的挂载目录: /usr/local/docker/promethues/se…...
Android 数据库之GreenDAO
GreenDAO 是一款开源的面向 Android 的轻便、快捷的 ORM 框架,将 Java 对象映射到 SQLite 数据库中,我们操作数据库的时候,不再需要编写复杂的 SQL语句, 在性能方面,greenDAO 针对 Android 进行了高度优化,…...
使用recyclerView显示forecast内容)
kotlin 编写一个简单的天气预报app(六)使用recyclerView显示forecast内容
要使用RecyclerView显示天气预报的内容 先在grandle里添加recyclerView的引用 implementation androidx.recyclerview:recyclerview:1.3.1创建一个RecyclerView控件:在布局文件中,添加一个RecyclerView控件,用于显示天气预报的列表。 这是一…...
jpa Page 1 of 0 containing UNKNOWN instances错误关于like问题的解决记录
导致这个问题的原因很多,这里记录一下我碰到的问题和解决方法。 网上有说时 pageNo要从0开始,我的不是这个问题。 在使用springboot jpa时,发现使用 t.ip like %?5% 语句,如果数据库记录的ip is null时,将查询不到该…...

Python实战之使用Python进行数据挖掘详解
一、Python数据挖掘 1.1 数据挖掘是什么? 数据挖掘是从大量的、不完全的、有噪声的、模糊的、随机的实际应用数据中,通过算法,找出其中的规律、知识、信息的过程。Python作为一门广泛应用的编程语言,拥有丰富的数据挖掘库&#…...

scala 加载properties文件
利用java.util.Properties加载 import java.io.FileInputStream import java.util.Properties object LoadParameter {//动态获取properties文件可配置参数val props new Properties()def getParameter(s:String,filePath:String): String {props.load(new FileInputStream(f…...
备战秋招012(20230808)
文章目录 前言一、今天学习了什么?二、动态规划1.概念2.题目 总结 前言 提示:这里为每天自己的学习内容心情总结; Learn By Doing,Now or Never,Writing is organized thinking. 提示:以下是本篇文章正文…...

QT中定时器的使用
文章目录 概述步骤 概述 Qt中使用定时器大致有两种,本篇暂时仅描述使用QTimer实现定时器 步骤 // 1.创建定时器对象 QTimer *timer new QTimer(this);// 2.开启一个定时器,5秒触发一次 timer->start(5000); // 3.建立信号槽连接&am…...
【UE4】多人联机教程(重点笔记)
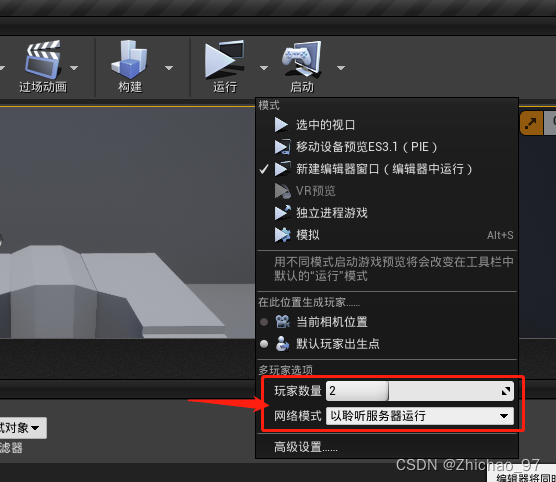
效果 1. 创建房间、搜索房间功能 2. 根据指定IP和端口加入游戏 步骤 1. 新建一个第三人称角色模板工程 2. 创建一个空白关卡,这里命名为“InitMap” 3. 新建一个控件蓝图,这里命名为“UMG_ConnectMenu” 在关卡蓝图中显示该控件蓝图 打开“UMG_Connec…...

【go】GIN参数重复绑定报错EOF问题
文章目录 1 问题描述2 解决:替换为ShouldBindBodyWith 1 问题描述 在 Gin 框架中,当多次调用 ShouldBind() 或 ShouldBindJSON() 方法时,会导致请求体的数据流被读取多次,从而出现 “EOF” 错误。 例如在api层绑定了参数&#x…...
关于MySQL中的binlog
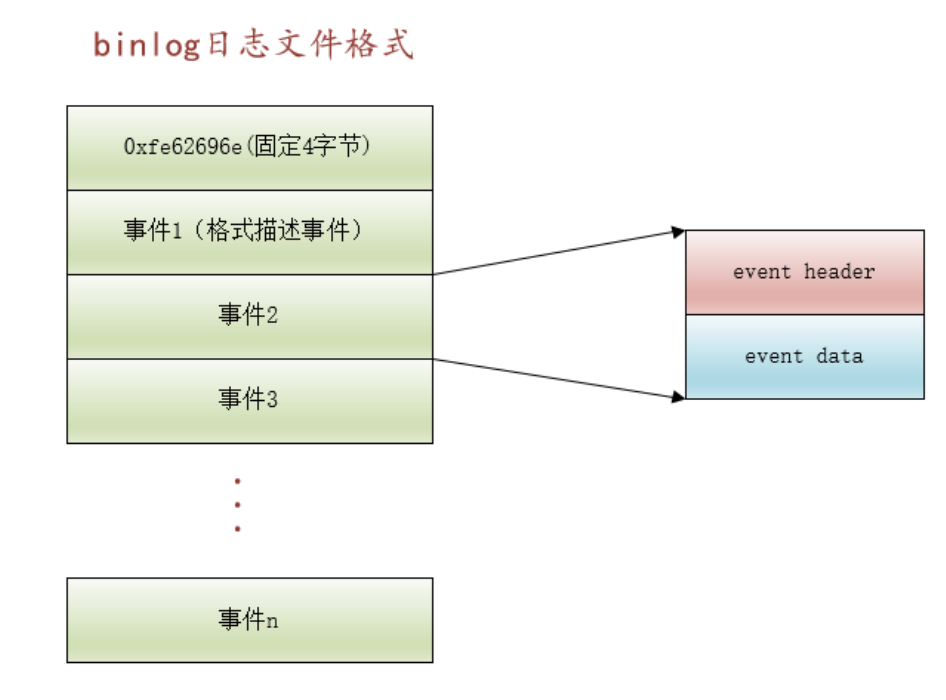
介绍 undo log 和 redo log是由Inno DB存储引擎生成的。 在MySQL服务器架构中,分为三层:连接层、服务层(server层)、执行层(存储引擎层) bin log 是 binary log的缩写,即二进制日志。 MySQL…...

我维护电脑的方法
无论是学习还是工作,电脑都是IT人必不可少的重要武器,一台好电脑除了自身配置要经得起考验,后期主人对它的维护也是决定它寿命的重要因素! 你日常是怎么维护你的“战友”的呢,维护电脑运行你有什么好的建议吗ÿ…...
AP51656 电流采样降压恒流驱动IC RGB PWM深度调光 LED电源驱动
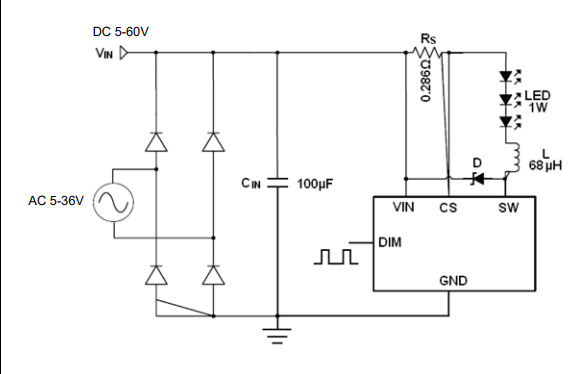
产品描述 AP51656是一款连续电感电流导通模式的降压恒流源,用于驱动一颗或多颗串联LED 输入电压范围从 5 V 到 60V,输出电流 可达 1.5A 。根据不同的输入电压和 外部器件, 可以驱动高达数十瓦的 LED。 内置功率开关,采用电流采样…...
Python爬虫的解析(学习于b站尚硅谷)
目录 一、xpath 1.xpath插件的安装 2. xpath的基本使用 (1)xpath的使用方法与基本语法(路径查询、谓词查询、内容查询(使用text查看标签内容)、属性查询、模糊查询、逻辑运算) (2&a…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
