现代C++中的从头开始深度学习【1/8】:基础知识
一、说明
提及机器学习框架与研究和工业的相关性。现在很少有项目不使用Google TensorFlow或Meta PyTorch,在于它们的可扩展性和灵活性。也就是说,花时间从头开始编码机器学习算法似乎违反直觉,即没有任何基本框架。然而,事实并非如此。自己对算法进行编码可以清晰而扎实地理解算法的工作原理以及模型真正在做什么。
在本系列中,我们将学习如何仅使用普通和现代C++编写必须知道的深度学习算法,例如卷积、反向传播、激活函数、优化器、深度神经网络等。

我们将通过学习一些现代 C++ 语言功能和相关编程细节来编码深度学习和机器学习模型,开始我们的故事之旅。
查看其他故事:
1 — Coding 2D convolutions in C++
2 — Cost Functions using Lambdas
3 — Implementing Gradient Descent
4 — Activation Functions
...更多内容即将推出。
我无法创造的,我不明白。— 理查德·费曼
二、新式C++、 和 标头<algorithm><numeric>
C++曾经是一种古老的语言,在过去十年中发生了翻天覆地的变化。主要变化之一是对函数式编程的支持。但是,还引入了其他几项改进,帮助我们开发更好、更快、更安全的机器学习代码。
为了我们在这里的任务,C++ 和 标头中包含一组方便的通用例程。作为一个说明性的例子,我们可以通过以下方式获得两个向量的内积:<numeric><algorithm>
#include <numeric>
#include <iostream>int main()
{std::vector<double> X {1., 2., 3., 4., 5., 6.};std::vector<double> Y {1., 1., 0., 1., 0., 1.};auto result = std::inner_product(X.begin(), X.end(), Y.begin(), 0.0);std::cout << "Inner product of X and Y is " << result << '\n';return 0;
}
并使用如下函数:accumulatereduce
std::vector<double> V {1., 2., 3., 4., 5.};double sum = std::accumulate(V.begin(), V.end(), 0.0);std::cout << "Summation of V is " << sum << '\n';double product = std::accumulate(V.begin(), V.end(), 1.0, std::multiplies<double>());std::cout << "Productory of V is " << product << '\n';double reduction = std::reduce(V.begin(), V.end(), 1.0, std::multiplies<double>());std::cout << "Reduction of V is " << reduction << '\n';
标头是大量有用的例程,例如,, , , ,等。让我们看一个说明性的例子:algorithmstd::transformstd::for_eachstd::countstd::uniquestd::sort
#include <algorithm>
#include <iostream>double square(double x) {return x * x;}int main()
{std::vector<double> X {1., 2., 3., 4., 5., 6.};std::vector<double> Y(X.size(), 0);std::transform(X.begin(), X.end(), Y.begin(), square);std::for_each(Y.begin(), Y.end(), [](double y){std::cout << y << " ";});std::cout << "\n";return 0;
}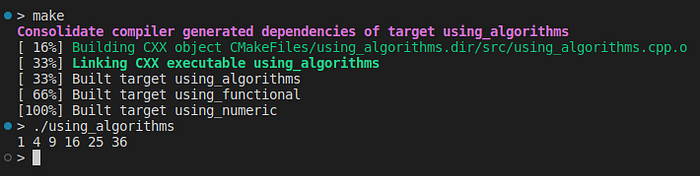
事实证明,在现代C++中,我们可以使用 、、 等函数,将函子、lambda 甚至香草函数作为参数传递,而不是显式使用 or 循环。forwhilestd::transformstd::for_eachstd::generate_n
上面的示例可以在 GitHub 上的此存储库中找到。
顺便说一下,是一个lambda。现在让我们谈谈函数式编程和lambda。[](double v){...}
三、函数式编程
C++是一种多范式编程语言,这意味着我们可以使用它来创建使用不同“样式”的程序,例如OOP,过程式和最近的功能。
对函数式编程的C++支持始于标头:<functional>
#include <algorithm> // std::for_each
#include <functional> // std::less, std::less_equal, std::greater, std::greater_equal
#include <iostream> // std::coutint main()
{std::vector<std::function<bool(double, double)>> comparators {std::less<double>(), std::less_equal<double>(), std::greater<double>(), std::greater_equal<double>()};double x = 10.;double y = 10.;auto compare = [&x, &y](const std::function<bool(double, double)> &comparator){bool b = comparator(x, y);std::cout << (b?"TRUE": "FALSE") << "\n";};std::for_each(comparators.begin(), comparators.end(), compare);return 0;
}
在这里,我们使用、、、和作为多态调用的示例,而不使用指针。std::functionstd::lessstd::less_equalstd::greaterstd::greater_equal
正如我们已经讨论过的,C++ 11 包括语言核心的更改以支持函数式编程。到目前为止,我们已经看到了其中之一:
auto compare = [&x, &y](const std::function<bool(double, double)> &comparator)
{bool b = comparator(x, y);std::cout << (b?"TRUE": "FALSE") << "\n";
};此代码定义一个 lambda,一个 lambda 定义一个函数对象,即可调用对象。
请注意 ,这不是 lambda 名称,而是 lambda 分配到的变量的名称。事实上,lambda 是匿名对象。
compare
此 lambda 由 3 个子句组成:捕获列表 ( )、参数列表 () 和正文(大括号之间的代码)。[&x, &y]const std::function<boll(double, double)> &comparator{...}
参数列表和 body 子句的工作方式与任何常规函数类似。捕获子句指定可在 lambda 主体中寻址的外部变量集。
Lambda 非常有用。我们可以像旧式函子一样声明和传递它们。例如,我们可以定义一个 L2 正则化 lambda:
auto L2 = [](const std::vector<double> &V)
{double p = 0.01;return std::inner_product(V.begin(), V.end(), V.begin(), 0.0) * p;
};并将其作为参数传递回我们的层:
auto layer = new Layer::Dense();
layer.set_regularization(L2)默认情况下,lambda 不会引起副作用,即它们不能更改外部内存空间中对象的状态。但是,如果需要,我们可以定义一个 lambda。考虑以下动量实现:mutable
#include <algorithm>
#include <iostream>using vector = std::vector<double>;int main()
{auto momentum_optimizer = [V = vector()](const vector &gradient) mutable {if (V.empty()) V.resize(gradient.size(), 0.);std::transform(V.begin(), V.end(), gradient.begin(), V.begin(), [](double v, double dx) {double beta = 0.7;return v = beta * v + dx; });return V;};auto print = [](double d) { std::cout << d << " "; };const vector current_grads {1., 0., 1., 1., 0., 1.};for (int i = 0; i < 3; ++i) {vector weight_update = momentum_optimizer(current_grads);std::for_each(weight_update.begin(), weight_update.end(), print);std::cout << "\n";}return 0;
}
每次调用都会产生不同的值,即使我们传递的值与参数相同。发生这种情况是因为我们使用关键字 .momentum_optimizer(current_grads)mutable
对于我们现在的目的,函数式编程范式特别有价值。通过使用功能特性,我们将编写更少但更健壮的代码,更快地执行更复杂的任务。
四、矩阵和线性代数库
好吧,当我说“纯C++”时,这并不完全正确。我们将使用可靠的线性代数库来实现我们的算法。
矩阵和张量是机器学习算法的构建块。C++中没有内置矩阵实现(也不应该有)。幸运的是,有几个成熟且优秀的线性代数库可用,例如 Eigen 和 Armadillo。
多年来,我一直在使用Eigen。Eigen(在Mozilla公共许可证2.0下)是仅标头的,不依赖于任何第三方库。因此,我将使用本征作为这个故事及以后的线性代数后端。
五、常见矩阵运算
最重要的矩阵运算是逐矩阵乘法:
#include <iostream>
#include <Eigen/Dense>int main(int, char **)
{Eigen::MatrixXd A(2, 2);A(0, 0) = 2.;A(1, 0) = -2.;A(0, 1) = 3.;A(1, 1) = 1.;Eigen::MatrixXd B(2, 3);B(0, 0) = 1.;B(1, 0) = 1.;B(0, 1) = 2.;B(1, 1) = 2.;B(0, 2) = -1.;B(1, 2) = 1.;auto C = A * B;std::cout << "A:\n" << A << std::endl;std::cout << "B:\n" << B << std::endl;std::cout << "C:\n" << C << std::endl;return 0;
}
通常称为 ,此操作的计算复杂度为 O(N³)。由于广泛用于机器学习,我们的算法受到矩阵大小的强烈影响。mulmatmulmat
让我们谈谈另一种类型的逐矩阵乘法。有时,我们只需要系数矩阵乘法:
auto D = B.cwiseProduct(C);
std::cout << "coefficient-wise multiplication is:\n" << D << std::endl;当然,在系数乘法中,参数的维度必须匹配。以同样的方式,我们可以添加或减去矩阵:
auto E = B + C;
std::cout << "The sum of B & C is:\n" << E << std::endl;
最后,让我们讨论三个非常重要的矩阵运算:、 和 :transposeinversedeterminant
std::cout << "The transpose of B is:\n" << B.transpose() << std::endl;
std::cout << "The A inverse is:\n" << A.inverse() << std::endl;
std::cout << "The determinant of A is:\n" << A.determinant() << std::endl;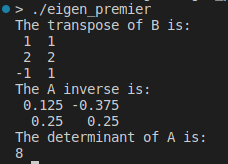
逆向、转置和行列式是实现我们的模型的基础。另一个关键点是将函数应用于矩阵的每个元素:
auto my_func = [](double x){return x * x;};
std::cout << A.unaryExpr(my_func) << std::endl;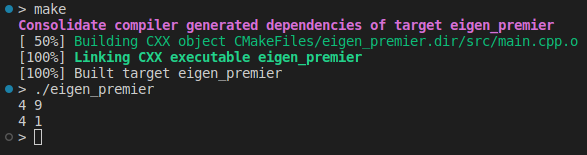
上面的例子可以在这里找到。
六、关于矢量化的一句话
现代编译器和计算机体系结构提供了称为矢量化的增强功能。简而言之,矢量化允许使用多个寄存器并行执行独立的算术运算。例如,以下 for 循环:
for (int i = 0; i < 1024; i++)
{A[i] = A[i] + B[i];
}以静默方式替换为矢量化版本:
for(i=0; i < 512; i += 2)
{ A[i] =A[i] + B[i];
A[i + 1] = A[i + 1] + B[i + 1 ];
} 由编译器。诀窍是指令与指令同时运行。这是可能的,因为两条指令彼此独立,并且底层硬件具有重复的资源,即两个执行单元。A[i + 1] = A[i + 1] + B[i + 1]A[i] = A[i] + B[i]
如果硬件有四个执行单元,编译器将按以下方式展开循环:
for(i=0; i < 256; i += 4)
{ A[i] =A[i] + B[i] ;
A[i + 1] = A[i + 1] + B[i + 1]; A[i + 2] = A[i + 2] + B[i + 2]; A[i + 3] = A[i + 3] + B[i + 3];
}与原始版本相比,此矢量化版本使程序运行速度提高了 4 倍。值得注意的是,这种性能提升不会影响原始程序的行为。
尽管矢量化是由编译器、操作系统和硬件在木头下执行的,但我们在编码时必须注意允许矢量化:
- 启用编译程序所需的矢量化标志
- 在循环开始之前,必须知道循环边界,动态或静态
- 循环体指令不应引用以前的状态。例如,诸如此类的事情可能会阻止矢量化,因为在某些情况下,编译器无法安全地确定在当前指令调用期间是否有效。
A[i] = A[i — 1] + B[i]A[i-1] - 循环体应由简单和直线代码组成。 还允许函数调用和先前矢量化的函数。但复杂的逻辑、子例程、嵌套循环和函数调用通常会阻止矢量化工作。
inline
在某些情况下,遵循这些规则并不容易。考虑到复杂性和代码大小,有时很难说编译器何时对代码的特定部分进行了矢量化处理。
根据经验,代码越精简和直接,就越容易被矢量化。因此,使用 、、 和 STL 容器的标准功能表示更有可能被矢量化的代码。<numeric>algorithmfunctional
七、机器学习中的矢量化
矢量化在机器学习中起着重要作用。例如,批次通常以矢量化方式处理,使具有大批次的火车比使用小批次(或不批处理)的火车运行得更快。
由于我们的矩阵代数库详尽地使用了矢量化,因此我们通常将行数据聚合成批次,以便更快地执行操作。请考虑以下示例:

与其在六个向量和一个向量中的每一个之间执行 6 个内积以获得 6 个输出 , 等等,我们可以堆叠输入向量以挂载一个包含六行的矩阵并使用单个乘法运行一次。XiVY0Y1MmulmatY = M*V
输出是一个向量。我们最终可以解绑它的元素以获得所需的 6 个输出值。Y
八、结论和下一步
这是一个关于如何使用现代C++编写深度学习算法的介绍性演讲。我们涵盖了高性能机器学习程序开发中非常重要的方面,例如函数式编程、代数演算和矢量化。
这里没有涉及现实世界 ML 项目的一些相关编程主题,例如 GPU 编程或分布式训练。我们将在以后的故事中讨论这些主题。
在下一个故事中,我们将学习如何编写2D卷积代码,这是深度学习中最基本的操作。
九、引用
C++参考资料
特征线性代数库
C++中的 Lambda 表达式
英特尔矢量化要点
相关文章:

现代C++中的从头开始深度学习【1/8】:基础知识
一、说明 提及机器学习框架与研究和工业的相关性。现在很少有项目不使用Google TensorFlow或Meta PyTorch,在于它们的可扩展性和灵活性。也就是说,花时间从头开始编码机器学习算法似乎违反直觉,即没有任何基本框架。然而,事实并非…...
Jwt(Json web token)——使用token的权限验证方法 用户+角色+权限表设计 SpringBoot项目应用
目录 引出使用token的权限验证方法流程 用户、角色、权限表设计权限表角色表角色-权限关联表用户表查询用户的权限(四表联查)数据库的视图 项目中的应用自定义注解拦截器controller层DTO返回给前端枚举类型的json化日期json问题 实体类-DAO 总结 引出 1.…...

SpringWeb项目核心功能总结
SpringWeb项目核心功能总结 文章目录 SpringWeb项目核心功能总结1.浏览器与Java程序的连接(个人偏好使用RequestMapping)2.参数的传入3.结果的返回请求转发和请求重定向的区别 核心功能用到的注解: RestControllerControllerResponseBodyRequ…...

Django------信号
Django 框架包含了一个信号机制,它允许若干个发送者(sender)通知一组接收者(receiver)某些特定操作或事件(events)已经发生了, 接收者收到指令信号(signals)后再去执行特定的操作。本文主要讲解Django信号(…...

HTML5 中新增了哪些表单元素?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ HTML5 中新增了的表单元素⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅!这个专栏是为那些对Web开发感兴趣、刚…...

[考研机试] KY20 完数VS盈数 清华大学复试上机题 C++实现
描述 一个数如果恰好等于它的各因子(该数本身除外)子和,如:6321。则称其为“完数”;若因子之和大于该数,则称其为“盈数”。 求出2到60之间所有“完数”和“盈数”。 输入描述: 题目没有任何输入。 输出描述&#…...
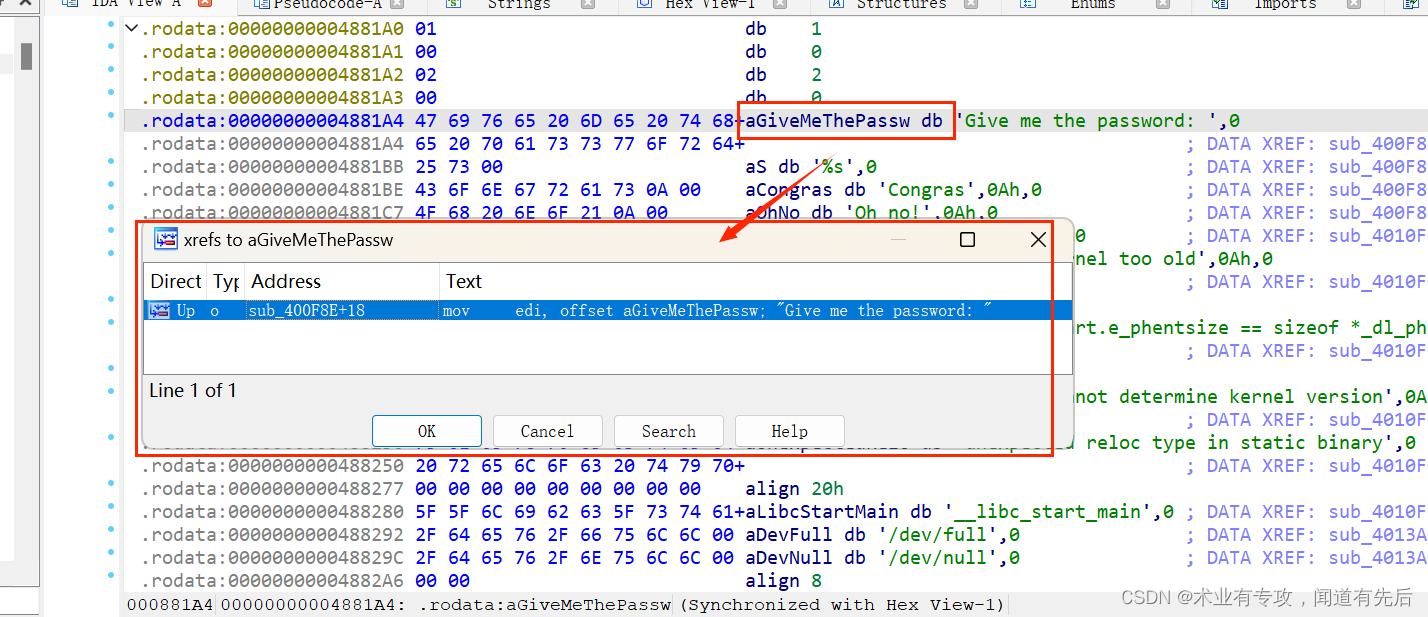
re学习(30)攻防世界-hackme(代码复原2)
思路: 1.输出成功,v26不为0,说明关系式:v21((unsigned __int8)v24 ^ v20) →2.在汇编代码第37行,输入v16v20,所以求的值为v20 →3.根据关系式,求的值v20v21^v24 →4.v21在第汇编代码第36行也可以提取出来…...
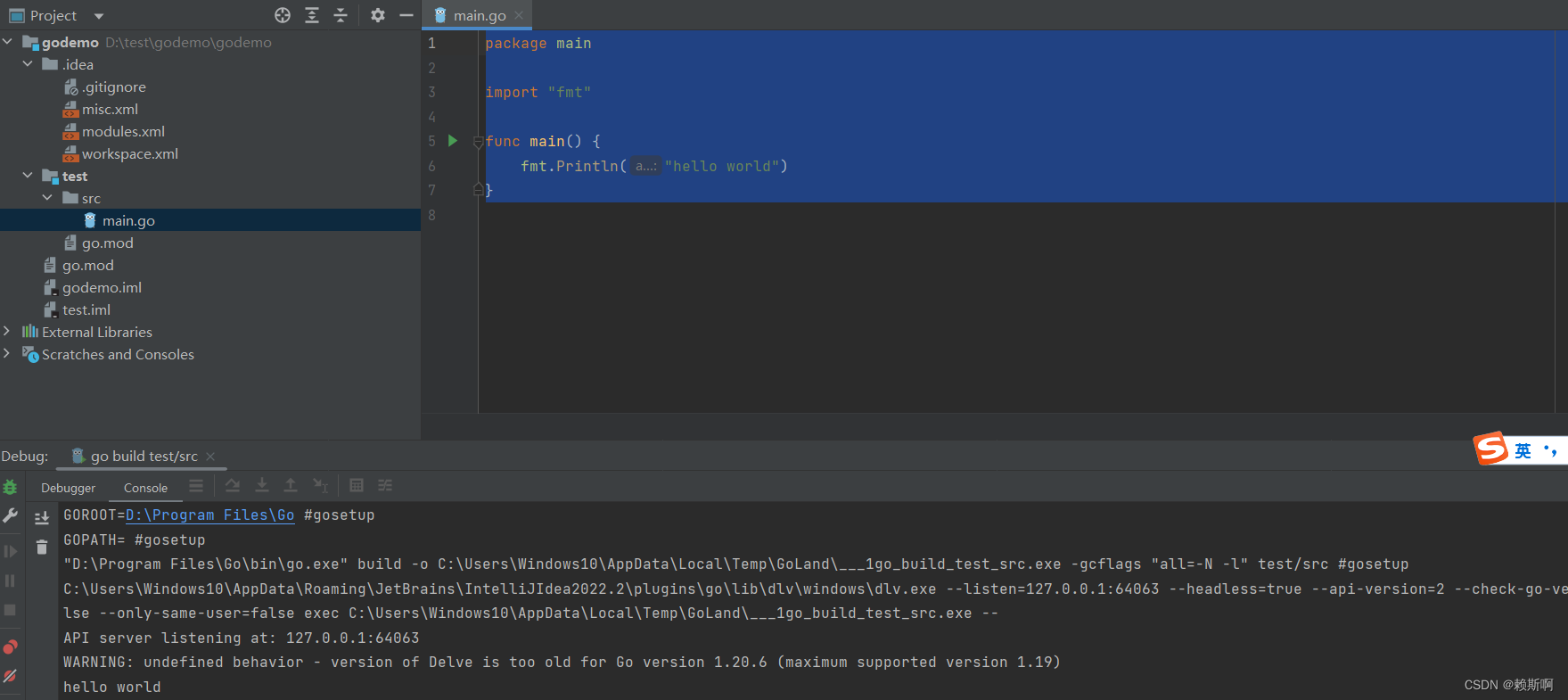
Go Windows下开发环境配置(图文)
Go Windows下开发环境配置 下载 安装 点击下载的安装包进行安装。安装路径可以选择到自己的目录。 环境变量配置 GOROOT:(指定到安装目录下) GOPATH:(是工作空间) path:在安装时已经添加了…...
)
【人工智能概述】python妙用 __str__()
【人工智能概述】python妙用 str() 文章目录 【人工智能概述】python妙用 __str__()一.python内置函数__str__() 一.python内置函数__str__() 通过自定义__str__()函数可以打印对象中相关的内容。 class Person(object):def __init__(self, name tom, age 10):self.name n…...

android kernel移植5-RK3568
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言1.添加开发板默认配置文件2.添加开发板默认设备树2.1复制设备树2.2指定设备树前言 前面我们已经学会了移植uboot,其实就是把瑞芯微的关于uboot的一些文件的名字和编译指定的文件改为自己定义…...

C++——string类介绍
我们知道在C语言里,字符串是以\0结尾的一些字符的集合,为了操作方便,C标准库中提供了一些str系列的库函数, 但是这些库函数与字符串是分离开的,而且底层空间需要用户自己管理,可 能还会越界访问。 但是在C…...
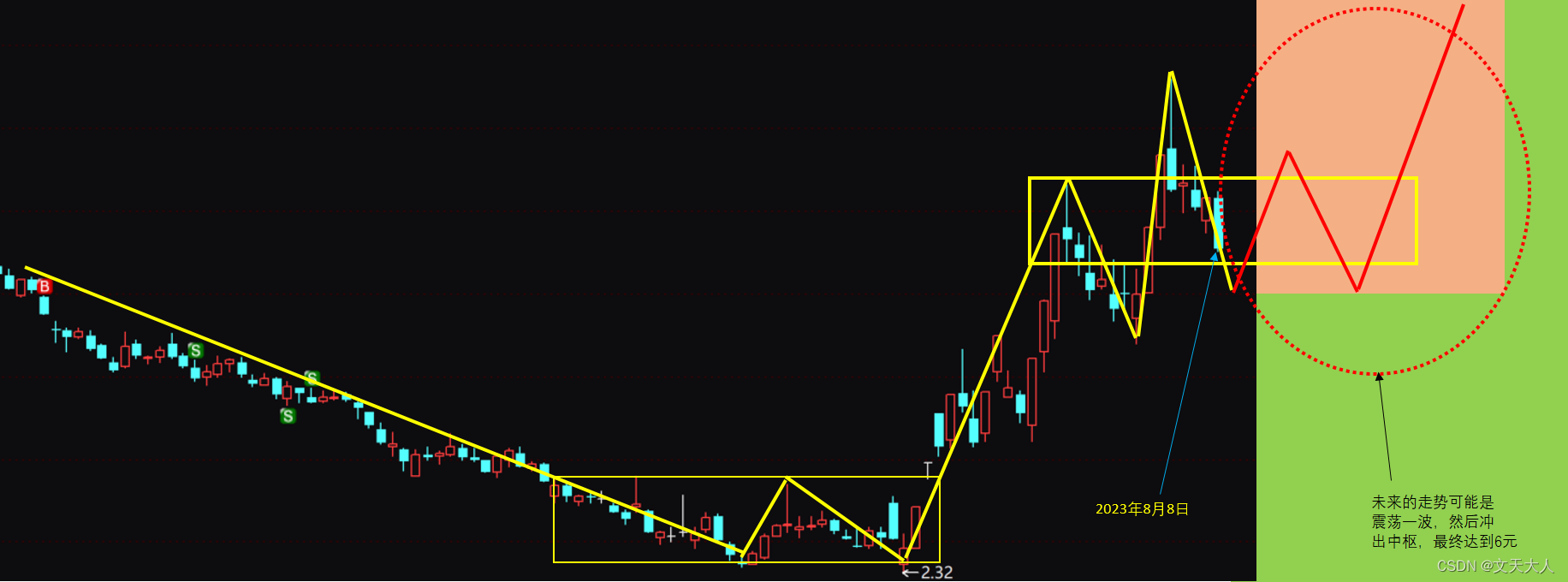
教雅川学缠论07-中枢实战众泰汽车000980
本文实战众泰汽车 下面是2023年11月14-2023年8月8众泰汽车日K图 先画日K 接下来处理包含,就变成下面这个样子 下面在套上缠论的理论,未来股价的走势应该是红色椭圆形虚线里面的样子 好了,文章就到这里,如果众泰最终不是这个走势…...

REDIS主从配置
目录 前言 一、概述 二、作用 三、缺点 四、redis主从复制的流程 五、搭建redis主从复制 总结 前言 Redis的主从配置是指在Redis集群中,将一个Redis节点配置为主节点(master),其他节点配置为从节点(slave)…...
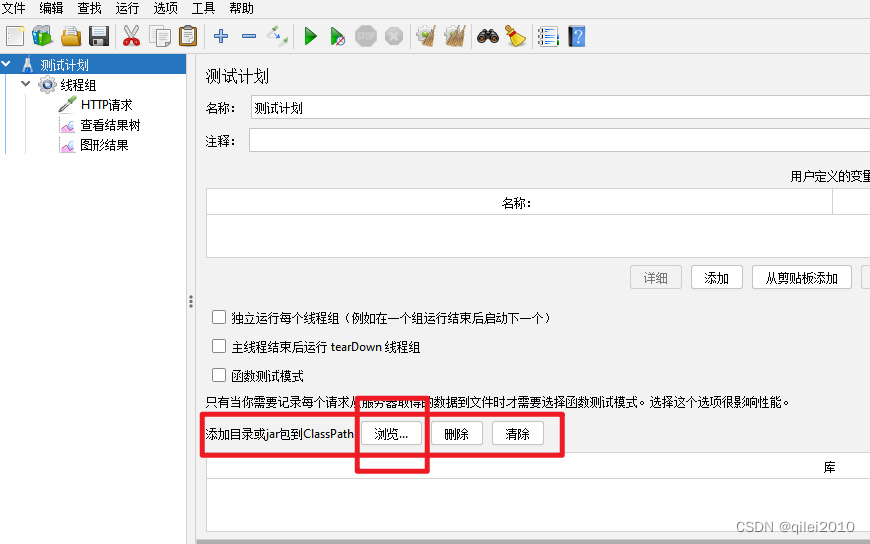
【测试】软件测试工具JMeter简单用法
简明扼要,点到为止。 1. JMeter介绍 JMeter的全称是Apache JMeter,是一款用于软件测试的工具软件,其是开源免费的,由Apache基金会运营。 官网:Apache JMeter - Apache JMeter™ 2. 下载安装及运行 2.1 安装 Java8…...

五个授权关键,为智能驾驶量产赋能
站在风口浪尖的智能驾驶行业? 智能汽车是指通过搭载先进传感器等装置,运用人工智能等新技术,具有自动驾驶功能,逐步成为智能移动空间和应用终端的新一代汽车。集中运用了计算机、现代传感、信息融合、通讯、人工智能及自动控制等技…...

【代码随想录-Leetcode第三题:977. 有序数组的平方】
题目 给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。 示例 1: 输入:nums [-4,-1,0,3,10] 输出:[0,1,9,16,100] 解释:平方后,数组…...
)
[运维|中间件] Apache APISIX Dashboard部署(持续踩坑更新。。。)
参考文献 Apache APISIX v2.6 官方文档 APISIX、APISIX Dashboard搭建、路由配置及插件使用 安装apisix和apisix-dashboard,访问方式,测试路由转发,反向代理等 文档地址 Dashboard Doc 下载地址 Apache APISIX Dashboard下载地址 部署 …...

Vue中watch监听属性新旧值相同问题解决方案
侦听器 _watch: 作用:可以侦听data和computed中数据的变化. 语法 watch: { "被侦听的属性名" (newVal, oldVal){ } } 监听简单数据类型时可以直接使用,而监听复杂数据类型时,例如当我们只需要监听data或者computed中对象的某个属性时,可以使用字符串的形式进行监听…...

awk案例练习
目录 一、awk练习 1.1筛选ip地址 1.2字段去重 1.3次数统计 1.4统计TCP连接状态 1.5处理字段缺失的数据 1.6筛选给定时间范围内的日志 一、awk练习 1.1筛选ip地址 ifconfig命令查看IP 利用awk进行筛选 ifconfig | awk BEGIN{RS""}NR2{print $6} RS指定输入记…...

Debian 12.1 正式发布
导读Debian 12.1 现已发布,这是对稳定发行版 Debian 12(代号 Bookworm )的首次更新。本次发布主要增加了安全问题的修正,并对严重问题进行了一些调整。 一些更新内容包括: 妥善处理系统用户的创建;修复 eq…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...
