leetcode做题笔记62
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
思路一:动态规划
int uniquePaths(int m, int n){int dp[m][n];int i,j=0;for(i=0;i<m;++i){for(j=0;j<n;++j){if(i==0||j==0){dp[i][j]=1;}else{dp[i][j]=dp[i-1][j]+dp[i][j-1];}}}return dp[m-1][n-1];
}时间复杂度O(mn),空间复杂度O(mn)
分析:
本题要求从左上角到右下角共有多少条不同路径,可利用动态规划,到每个格子的不同路径等于到左边前一个路径数加上边前一个路径数,最后返回dp[m-1][n-1]
思路二:组合排列
int Combinations(int up, int down){long prod = 1;int left = down - up + 1, right = 1;while(right <= up){prod *= left;prod /= right;left++;right++;}return prod;
}int uniquePaths(int m, int n){int para = (m - 1 < n - 1) ? m - 1 : n - 1;return Combinations(para, m + n - 2);
}时间复杂度O(n),空间复杂度O(1)
分析:
本题同时可直接用排列组合进行计算,因为机器人需要向下走n-1步,向右走m-1步,即共走m+n-2步中间有n-1步向下走,计算即可得到答案。
比较:
两个思路比较,组合排列的方式可直接计算结果,避免构造数组,在内存方面占优,且组合排列计算的时间复杂度为O(n)优于第一种不断向后递推的思路,运行速度更快。
总结:
本题考察动态规划的应用,每个格子考虑左边前一个和上边前一个的值,或直接使用组合排列的方法得到答案。
相关文章:

leetcode做题笔记62
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。 问总共有多少条不同的路径? 思路一…...

图论 <最短路问题>模板
图论 <最短路问题> 有向图 1.邻接矩阵,稠密图 2.邻接表 (常用)单链表,每一个点都有一个单链表 ,插入一般在头的地方插, 图的邻接表的存储方式 树的深度优先遍历 特殊的深度优先搜索,…...
计算机网络性能指标
比特:数据量的单位 KB 2^10B 2^13 bit 比特率:连接在计算机网络上的主机在数字通道上传送比特的速率 kb/s 10^3b/s 带宽:信号所包含的各种频率不同的成分所占据的频率范围 Hz 表示在网络中的通信线路所能传送数据的能力(…...

vue + elementUI 实现下拉树形结构选择部门,支持多选,支持检索
vue elementUI 实现下拉树形结构选择部门,支持多选,支持检索 <template><div><el-select v-model"multiple?choosedValue:choosedValue[0]" element-loading-background"rgba(0,0,0,0.8)":disabled"disableFl…...
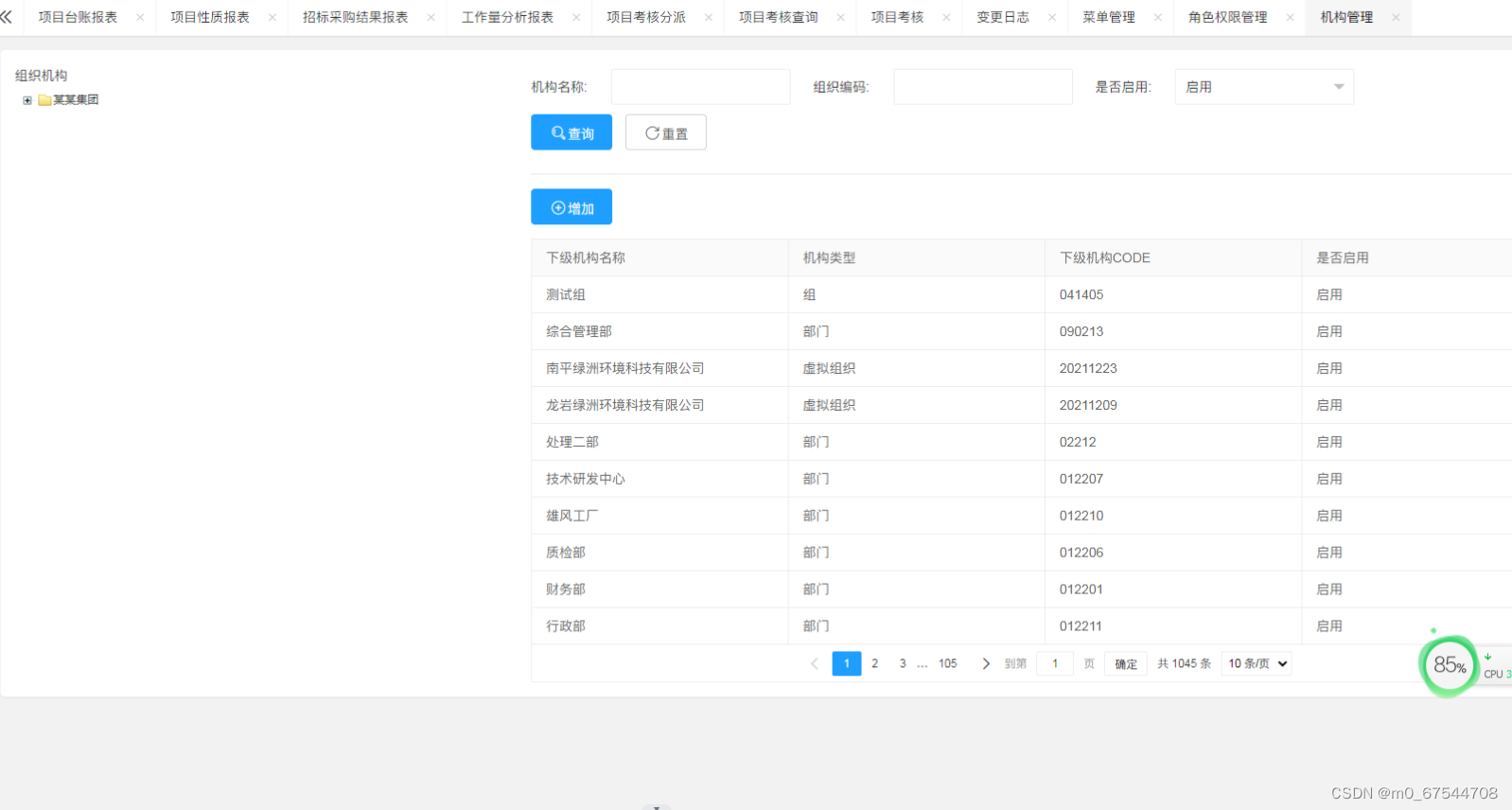
招投标系统简介 企业电子招投标采购系统源码之电子招投标系统 —降低企业采购成本 tbms
功能模块: 待办消息,招标公告,中标公告,信息发布 描述: 全过程数字化采购管理,打造从供应商管理到采购招投标、采购合同、采购执行的全过程数字化管理。通供应商门户具备内外协同的能力,为外…...
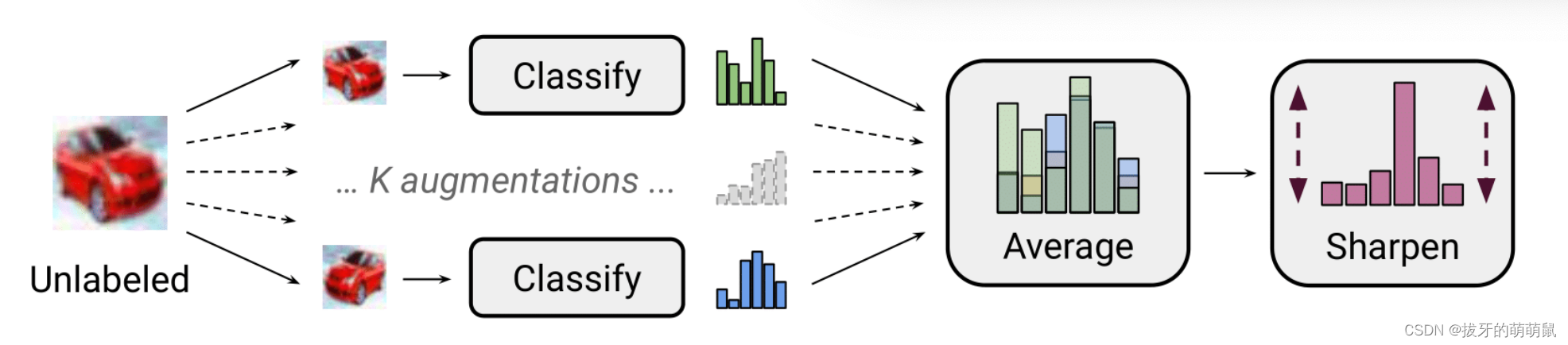
半监督学习(主要伪标签方法)
半监督学习 1. 引言 应用场景:存在少量的有标签样本和大量的无标签样本的场景。在此应用场景下,通常标注数据是匮乏的,成本高的,难以获取的,与之相对应的是却存在大量的无标注数据。半监督学习的假设:决策…...
)
datePicker一个或多个日期组件,如何快捷选择多个日期(时间段)
elementUI的组件文档中没有详细说明type"dates"如何快捷选择一个时间段的日期,我们可以通过picker-options参数来设置快捷选择: <div class"block"><span class"demonstration">多个日期</span><el…...

【语音合成】微软 edge-tts
目录 1. edge-tts 介绍 2. 代码示例 1. edge-tts 介绍 https://github.com/rany2/edge-tts 在Python代码中使用Microsoft Edge的在线文本到语音服务 2. 代码示例 import asyncio # pip install edge_tts import edge_tts TEXT """给我放首我喜欢听的歌曲…...

elevation mapping学习笔记3之使用D435i相机离线或在线订阅点云和tf关系生成高程图
文章目录 0 引言1 数据1.1 D435i相机配置1.2 协方差位姿1.3 tf 关系2 离线demo2.1 yaml配置文件2.2 launch启动文件2.3 数据录制2.4 离线加载点云生成高程图3 在线demo3.1 launch启动文件3.2 CMakeLists.txt3.3 在线加载点云生成高程图0 引言 elevation mapping学习笔记1已经成…...
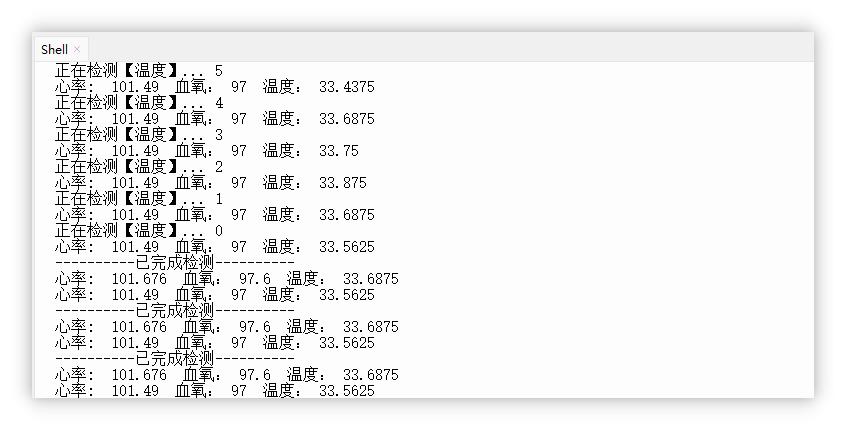
ESP32 Max30102 (3)修复心率误差
1. 运行效果 2. 新建修复心率误差.py 代码如下: from machine import sleep, SoftI2C, Pin, Timer from utime import ticks_diff, ticks_us from max30102 import MAX30102, MAX30105_PULSE_AMP_MEDIUM from hrcalc import calc_hr_and_spo2BEATS = 0 # 存储心率 FINGER_F…...

16-4_Qt 5.9 C++开发指南_Qt 应用程序的发布
文章目录 1. 应用程序发布方式2. Windows 平台上的应用程序发布 1. 应用程序发布方式 用 Qt 开发一个应用程序后,将应用程序提供给用户在其他计算机上使用就是应用程序的发布。应用程序发布一般会提供一个安装程序,将应用程序的可执行文件及需要的运行库…...

oracle容灾备份怎么样Oracle容灾备份
随着科学技术的发展和业务的增长,数据安全问题越来越突出。为了保证数据的完整性、易用性和保密性,公司需要采取一系列措施来防止内容丢失的风险。 Oracle是一个关系数据库管理系统(RDBMS),OracleCorporation是由美国软件公司开发和维护的。该系统功能…...

AcWing 4957:飞机降落
【题目来源】https://www.acwing.com/problem/content/4960/【题目描述】 有 N 架飞机准备降落到某个只有一条跑道的机场。 其中第 i 架飞机在 Ti 时刻到达机场上空,到达时它的剩余油料还可以继续盘旋 Di 个单位时间,即它最早可以于 Ti 时刻开始降落&…...

强化学习研究 PG
由于一些原因, 需要学习一下强化学习。用这篇博客来学习吧, 用的资料是李宏毅老师的强化学习课程。 深度强化学习(DRL)-李宏毅1-8课(全)_哔哩哔哩_bilibili 这篇文章的目的是看懂公式, 毕竟这是我的弱中弱。 强化…...

uniapp微信小程序 401时重复弹出登录弹框问题
APP.vue 登陆成功后,保存登陆信息 if (res.code 200) {uni.setStorageSync(loginResult, res)uni.setStorageSync(token, res.token);uni.setStorageSync(login,false);uni.navigateTo({url: "/pages/learning/learning"}) }退出登录 toLogout: func…...
Cloud Studio实战——热门视频Top100爬虫应用开发
最近Cloud Studio非常火,我也去试了一下,感觉真的非常方便!我就以Python爬取B站各区排名前一百的视频,并作可视化来给大家分享一下Cloud Studio!应用链接:Cloud Studio实战——B站热门视频Top100爬虫应用开…...

php 去除二维数组重复
在 PHP 中,我们常常需要对数组进行处理和操作。有时候,我们需要去除数组中的重复元素,这里介绍一种针对二维数组的去重方法。 以下是列举一些常见的方法: 方法一:使用 array_map 和 serialize 函数 array_map 函数可以…...
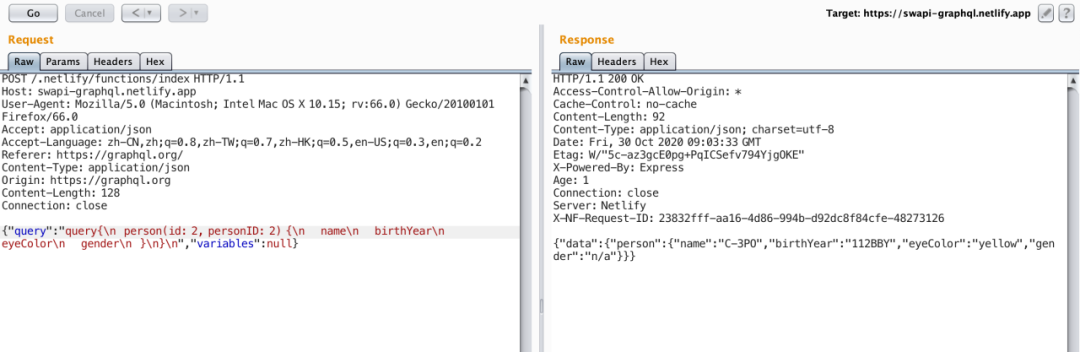
玩转graphQL
转载至酒仙桥的玩转graphQL - SecPulse.COM | 安全脉搏 前言 在测试中我发现了很多网站开始使用GraphQL技术,并且在测试中发现了其使用过程中存在的问题,那么,到底GraphQL是什么呢?了解了GraphQL后能帮助我们在渗透测试中发现哪些…...
.__init__()的含义)
神经网络super(XXX, self).__init__()的含义
学习龙良曲老师的课程,在77节有这样一段代码 import torch from torch import nnclass Lenet5(nn.Module):def __init__(self):super(Lenet5,self).__init__()那么,super(XXX, self).init()的含义是什么? Python中的super(Net, self).init()…...
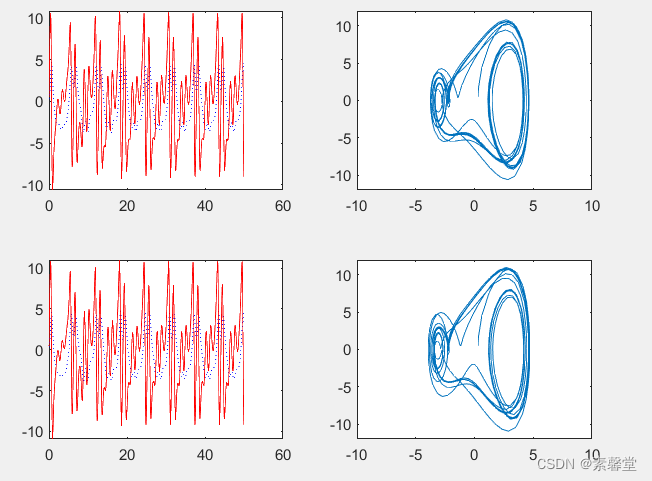
45.杜芬方程解仿真解曲线(matlab程序)
1.简述 Dufing方程是一种重要的动力系统山,是反映工程物理系统中非线性现象和混沌动力学行为的极其重要的方程式。通过Duffing方程可以探讨铁磁谐振电路中的分岔、拟周期运动、子谐波振荡。而在非线性与混沌系统的研究中,Duffing方程展示了丰富的混沌动力…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...
