无涯教程-Perl - fcntl函数
描述
该函数是系统fcntl()函数的Perl版本。使用FILEHANDLE上的SCALAR执行FUNCTION指定的功能。 SCALAR包含函数要使用的值,或者是任何返回信息的位置。
语法
以下是此函数的简单语法-
fcntl FILEHANDLE, FUNCTION, SCALAR
返回值
该函数返回0,但如果fcntl()的返回值为0,则返回true,系统返回该值,失败则返回undef。
Perl 中的 fcntl函数 - 无涯教程网无涯教程网提供描述该函数是系统fcntl()函数的Perl版本。使用FILEHANDLE上的SCALAR执行FUNCTION指定...
https://www.learnfk.com/perl/perl-fcntl.html
相关文章：
无涯教程-Perl - fcntl函数
描述 该函数是系统fcntl()函数的Perl版本。使用FILEHANDLE上的SCALAR执行FUNCTION指定的功能。 SCALAR包含函数要使用的值,或者是任何返回信息的位置。 语法 以下是此函数的简单语法- fcntl FILEHANDLE, FUNCTION, SCALAR返回值 该函数返回0,但如果fcntl()的返回值为0,则返…...
docker 命令解析
docker命令解析的文章参考 build 和 commit build适合从头创建一个清晰干净的镜像。 build是从Dockfile产生新的镜像，对于使用者能清晰的知道镜像中包含了哪些内容。commit适合将已有的容器打包提供给其他使用者。 commit是从已经存在的容器产生镜像，这…...
Map集合 实体类对象的相互转换
一、Map转实体类 1. fastjson工具类 导入依赖 <dependency><groupId>com.alibaba</groupId><artifactId>fastjson</artifactId><version>1.2.54</version> </dependency>代码实现 Map<String, Object> authorMap n…...
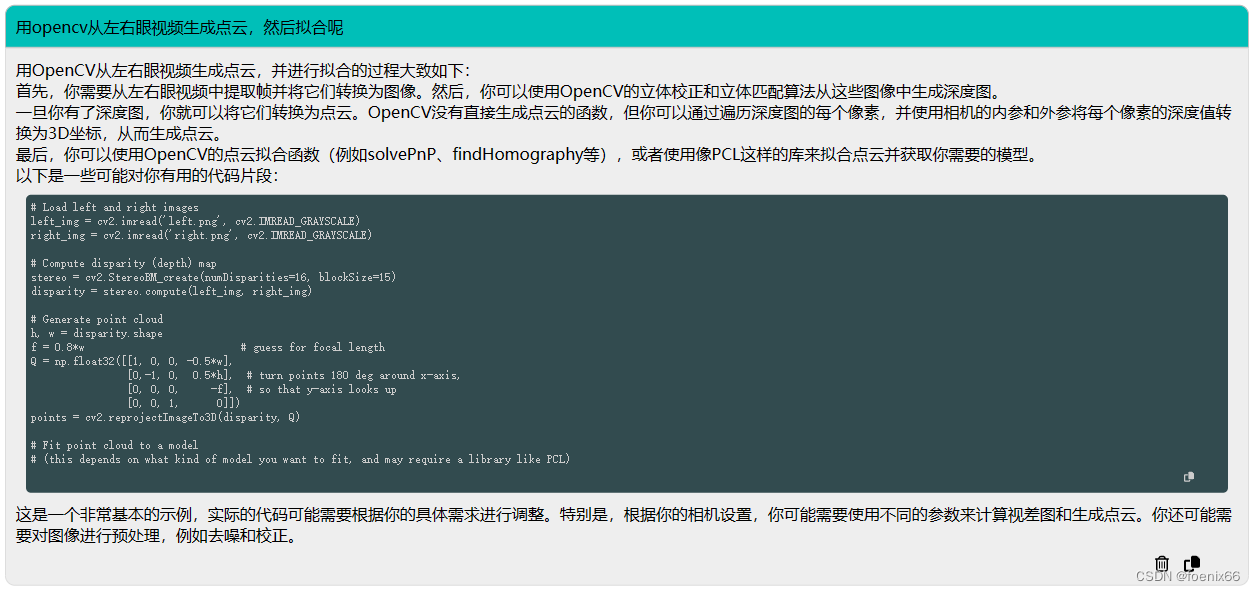
用chatGPT从左右眼图片生成点云数据
左右眼图片 需求 需要将左右眼图像利用视差生成三维点云数据 先问问chatGPT相关知识 进一步问有没有现成的软件 chatGPT提到了OpenCV，我们让chatGPT用OpenCV写一个程序来做这个事情 当然，代码里面会有一些错误，chatGPT写的代码并不会做模…...
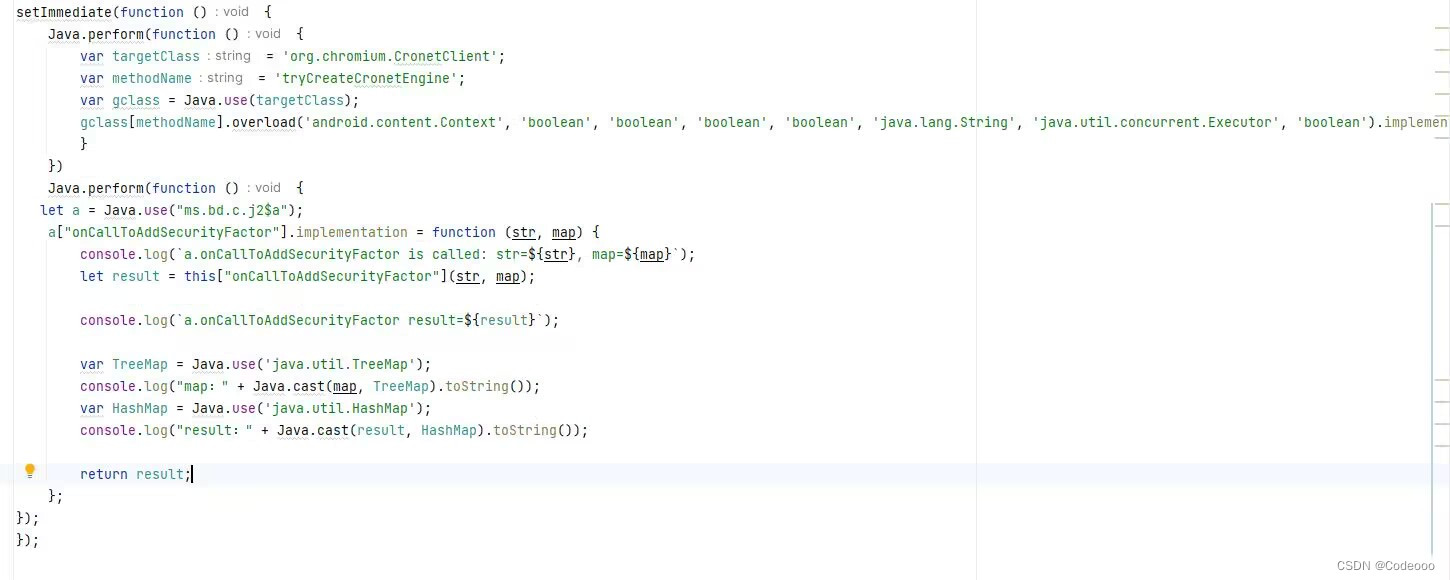
dy六神参数记录分析（立秋篇）
version： 23.9 X-SSSTUB: 搜索：x-tt-dt var hashMap Java.use("java.util.HashMap");hashMap.put.implementation function (a, b) {console.log("hashMap.put: ", a, b);return this.put(a, b);}https://codeooo.blog.csdn.n…...
微信-jssdk使用
需求: h5中使用微信的jsSDK,后续实现微信定位以及多图上传 微信文档 申请测试公众号 1.测试公众号进行配置 其中的域名是本地的ip地址 config接口进行权限配置，动态获取JS-SDK权限验证的签名 获取公众号accessToken以及jsTicket public static String WeChatAppId="wx…...
guava-retry使用笔记
guava-retry使用笔记 xml依赖 <dependency><groupId>com.github.rholder</groupId><artifactId>guava-retrying</artifactId><version>2.0.0</version> </dependency>使用案例 重试3次，每次间隔3秒 /*** 重试…...
P1226 【模板】快速幂 | 取余运算
【模板】快速幂 | 取余运算 题目描述 给你三个整数 a , b , p a,b,p a,b,p，求 a b m o d p a^b \bmod p abmodp。 输入格式 输入只有一行三个整数，分别代表 a , b , p a,b,p a,b,p。 输出格式 输出一行一个字符串 a^b mod ps，其中 …...
常用开源的弱口令检查审计工具
常用开源的弱口令检查审计工具 1、SNETCracker 1.1、超级弱口令检查工具 SNETCracker超级弱口令检查工具是一款开源的Windows平台的弱口令安全审计工具，支持批量多线程检查，可快速发现弱密码、弱口令账号，密码支持和用户名结合进行检查&am…...
云监控插件cloudmonitor安装保姆级教程
1、 需要isv把这些域名和ip加入到hosts中； 192.168.31.61 update.aegis.cloud.jiashan.gov.cn； 192.168.31.61 update.aegis.aliyun.com； 192.168.31.61 update2.aegis.cloud.jiashan.gov.cn； 192.168.31.61 update2.aegis.aliyun…...
借用和引用
文章目录 所有权引用和借用可变引用悬垂引用 所有权 Rust通过所有权来管理内存，最妙的是，这种检查只发生在编译期，因此对于程序运行期，不会有任何性能上的损失。 使用堆和栈的性能区别： 写入方面：入栈比在…...
WPF上位机9——Lambda和Linq
Lambda Linq 操作集合 使用类sql形式查询 Linq To SQL...
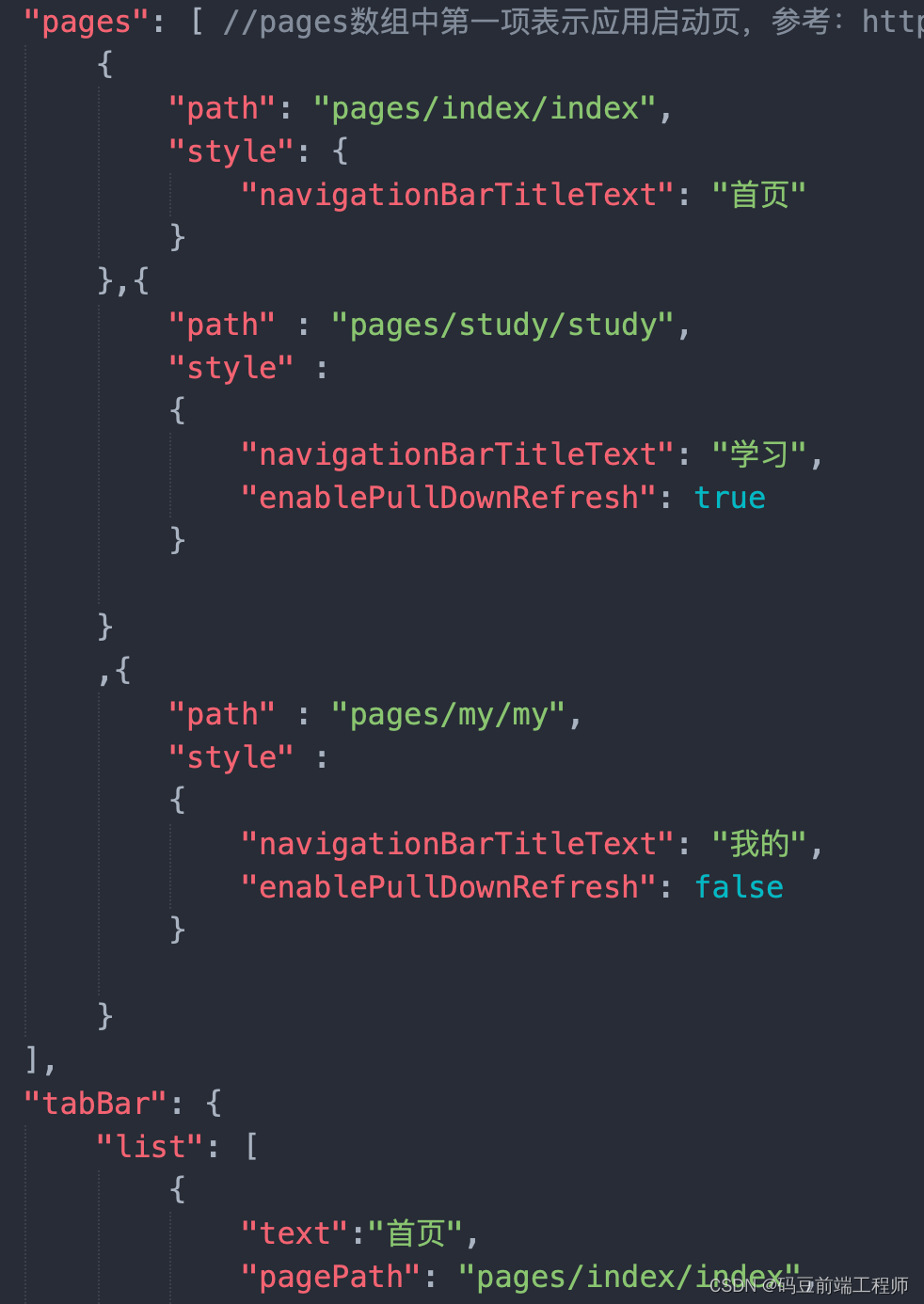
从0到1搭建uniapp
一、什么是uniapp UniApp是一款基于Vue.js框架的全端开发工具，可以实现同时开发多个平台（包括H5、小程序、APP等）应用的能力。使用UniApp，开发者只需要编写一份代码就可以快速地发布到多个平台，极大地提高了开发效率和…...
安全杂记 - Linux文本三剑客之awk
目录 1.什么是AWK2.正则表达式3.语法4.内置变量示例printf命令5.复现awk经典实例(1).插入几个新字段(2).格式化空白(3).筛选IPv4地址(4).筛选给定时间范围内的日志 1.什么是AWK awk、grep、sed是linux操作文本的三大利器，合称文本三剑客。三者的功能都是处理文本&a…...
Android 开发者选项日志存储路径
android开发者选项中存在两个item是关于系统日志的。 1.日志记录器缓冲区大小 2.在设备上永久存储日志记录器数据 一个是用来设置缓冲区大小，一个是用来日志存储开关及过滤。 通过分析 system/core/logcat/logcatd.rc mkdir /data/misc/logd 0770 logd log 日志的…...
jupyter lab build失败，提示需要安装版本＞=12.0.0的nodejs但其实已从官网安装18.17.0版本 的解决方法
出现的问题如题目所示，这个问题差点要把我搞死了。。。但还是在没有重装的情况下解决了😘。 问题来源 初衷是想安装lsp扩展，直接在jupyter lab网页界面的extensions中搜索lsp并点击install krassowski/jupyterlab-lsp，会提示需要…...
【set】个人练习-Leetcode-817. Linked List Components
题目链接：https://leetcode.cn/problems/linked-list-components/description/ 题目大意：给出一个vector<int> nums，其中有一些数字。再给出一个链表的头指针head，链表内的元素各不相同。如果链表中有某一段（长…...
Linux IPIP隧道连通两个局域网
拓扑结构 现有两台主机，它们具有两个网口分别接入到不同网络中。 主机A： eth0：处于 10.0.1.2/24 网段eth1： 处于192.168.1.100/24 网段 主机B： eth0：处于10.0.2.3/24 网段eth1： 处于192.168.2…...
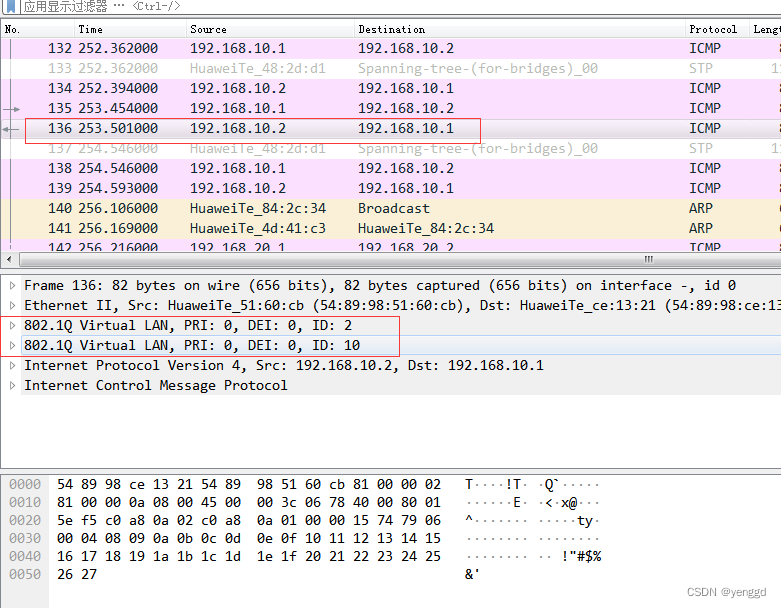
华为QinQ技术的基本qinq和灵活qinq 2种配置案例
基本qinq配置： 运营商pe设备在收到同一个公司的ce发来的的包，统一打上同样的vlan ，如上图，同一个家公司两边统一打上vlan 2，等于在原内网vlan 10或20过来的包再统一打上vlan 2的标签，这样传输就不会和其它…...
python爬虫1：基础知识
python爬虫1：基础知识 前言 python实现网络爬虫非常简单，只需要掌握一定的基础知识和一定的库使用技巧即可。本系列目标旨在梳理相关知识点，方便以后复习。 目录结构 文章目录 python爬虫1：基础知识1. 基础认知1.1 什么是爬虫&…...
Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中，接口是一种抽象类型，它定义了一组方法的集合： // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的： // 矩形结构体…...
【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类：块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...
CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库，而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例，演示如何： 使用 FetchContent 从 GitH…...
使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型（LLM）的广泛应用，开发者常面临多个挑战： 各大模型（OpenAI、Claude、Gemini、Ollama）接口风格不统一；缺乏一个统一平台进行模型调用与测试；本地模型 Ollama 的集成与前…...
以光量子为例，详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学（silicon photonics）的光波导（optical waveguide）芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中，光既是波又是粒子。光子本…...
七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...
Proxmox Mail Gateway安装指南：从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客，很高兴能够在这里和您见面！希望您在这里可以感受到一份轻松愉快的氛围，不仅可以获得有趣的内容和知识，也可以畅所欲言、分享您的想法和见解。 推荐：「storms…...
五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏，有着深厚的文化底蕴。通过将五子棋制作成网页游戏，可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家，都可以通过网页五子棋感受到东方棋类…...
热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日，在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上，可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞，强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...
【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖，添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...