现代C++中的从头开始深度学习:【5/8】卷积
一、说明
现在,让我们通过使用 2D 卷积实现实际编码深度学习模型来开始我们的道路。让我们开始吧。
二、关于本系列
我们将学习如何仅使用普通和现代C++对必须知道的深度学习算法进行编码,例如卷积、反向传播、激活函数、优化器、深度神经网络等。

查看其他故事:
0 — 现代C++深度学习编程基础
2 — 使用 Lambda 的成本函数
3 — 实现梯度下降
4 — 激活函数
...更多内容即将推出。
三、卷 积
卷积是信号处理领域的老朋友。最初,它的定义如下:

在机器学习术语中:
- 我(...通常称为输入
- K(...作为内核,以及
- F(...)作为给定 K 的 I(x) 的特征映射。
考虑一个多维离散域,我们可以将积分转换为以下求和:
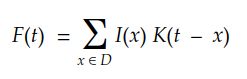
最后,对于2D数字图像,我们可以将其重写为:

理解卷积的一种更简单的方法是下图:
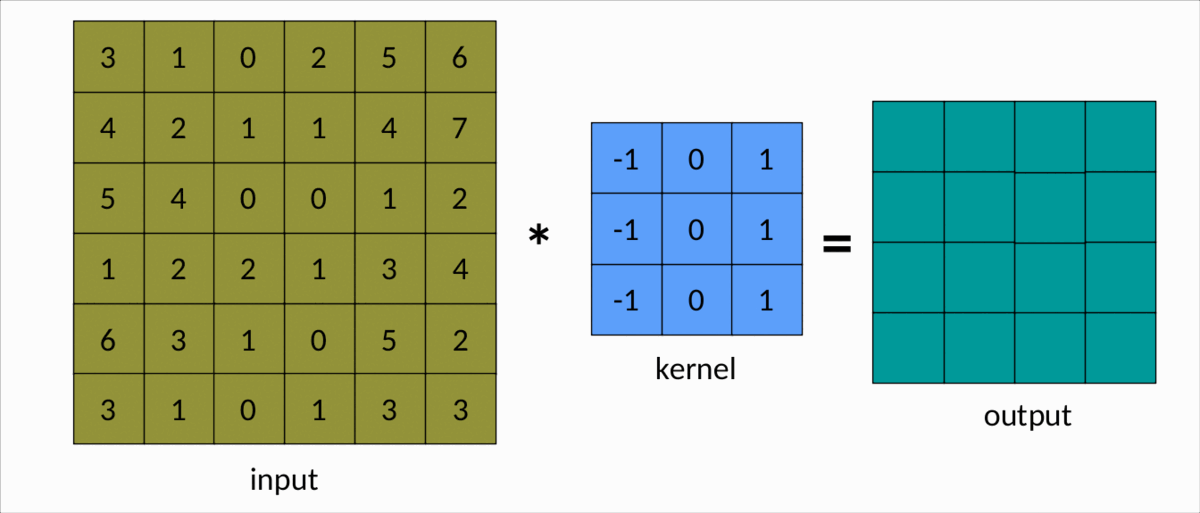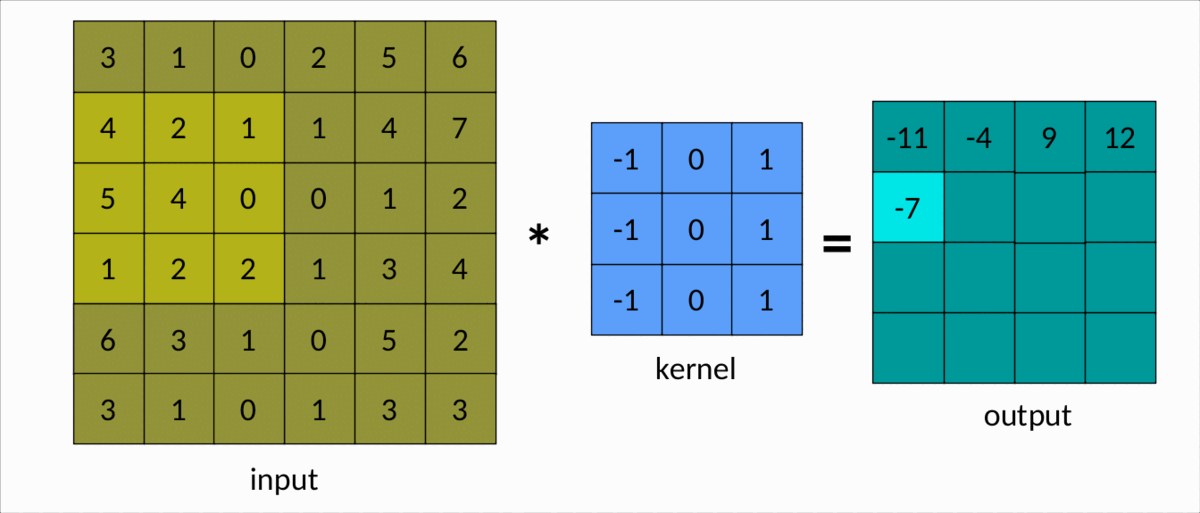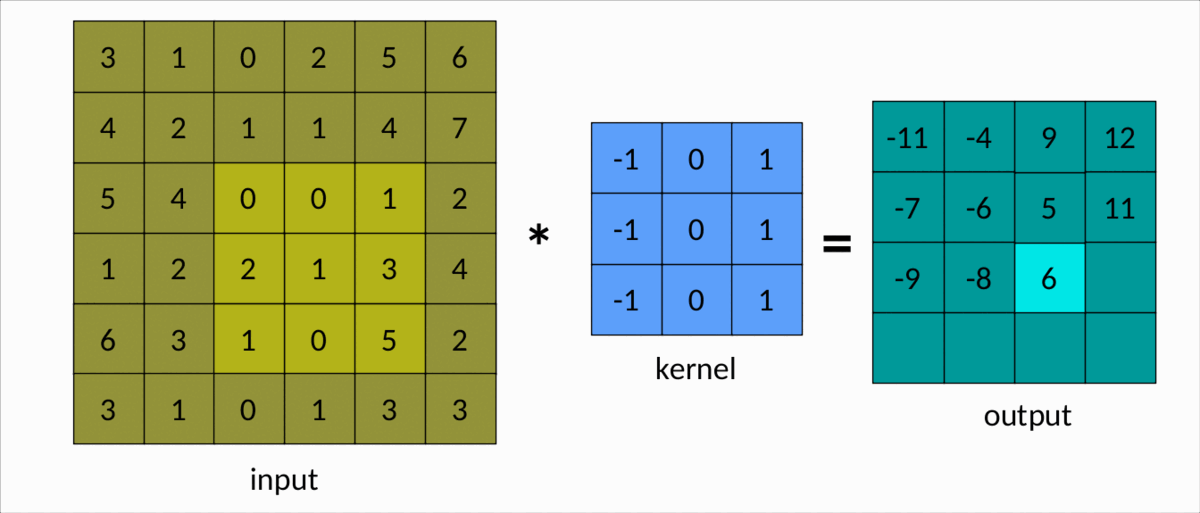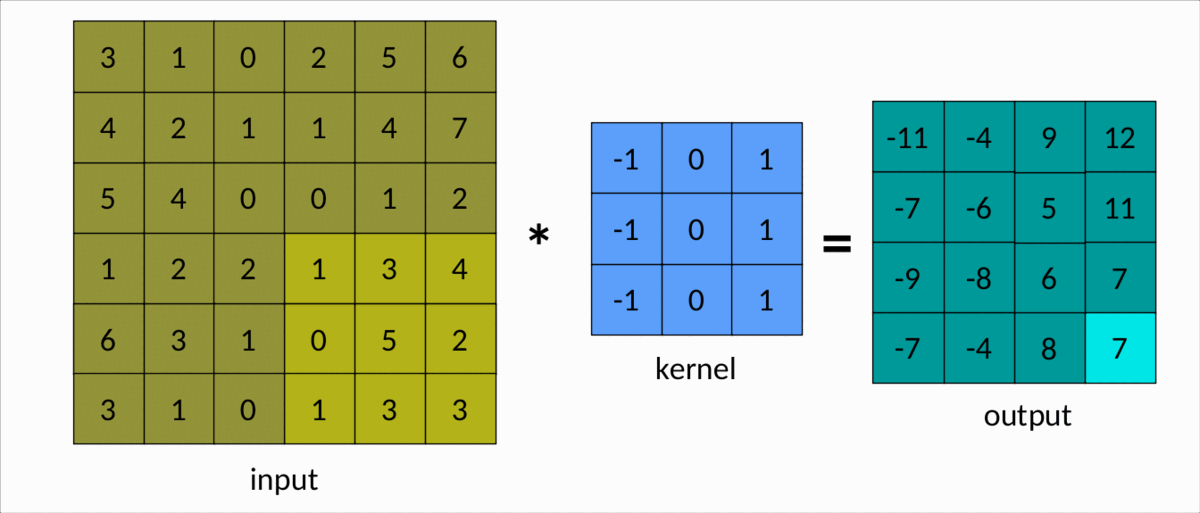
我们可以很容易地看到内核在输入矩阵上滑动,生成另一个矩阵作为输出。这是卷积的简单情况,称为有效卷积。在这种情况下,矩阵的维度由下式给出:Output
dim(Output) = (m-k+1, n-k+1)
这里:
m分别是输入矩阵中的行数和列数,以及nk是平方核的大小。
现在,让我们对第一个 2D 卷积进行编码。
四、使用循环对 2D 卷积进行编码
实现卷积的最直观方法是使用循环:
auto Convolution2D = [](const Matrix &input, const Matrix &kernel)
{const int kernel_rows = kernel.rows();const int kernel_cols = kernel.cols();const int rows = (input.rows() - kernel_rows) + 1;const int cols = (input.cols() - kernel_cols) + 1;Matrix result = Matrix::Zero(rows, cols);for (int i = 0; i < rows; ++i) {for (int j = 0; j < cols; ++j) {double sum = input.block(i, j, kernel_rows, kernel_cols).cwiseProduct(kernel).sum();result(i, j) = sum;}}return result;
};这里没有秘密。我们将内核滑过列和行,为每个步骤应用内积。现在,我们可以像以下那样简单地使用它:
#include <iostream>
#include <Eigen/Core>using Matrix = Eigen::MatrixXd;auto Convolution2D = ...;int main(int, char **)
{Matrix kernel(3, 3);kernel << -1, 0, 1,-1, 0, 1,-1, 0, 1;std::cout << "Kernel:\n" << kernel << "\n\n";Matrix input(6, 6);input << 3, 1, 0, 2, 5, 6,4, 2, 1, 1, 4, 7,5, 4, 0, 0, 1, 2,1, 2, 2, 1, 3, 4,6, 3, 1, 0, 5, 2,3, 1, 0, 1, 3, 3;std::cout << "Input:\n" << input << "\n\n";auto output = Convolution2D(input, kernel);std::cout << "Convolution:\n" << output << "\n";return 0;
}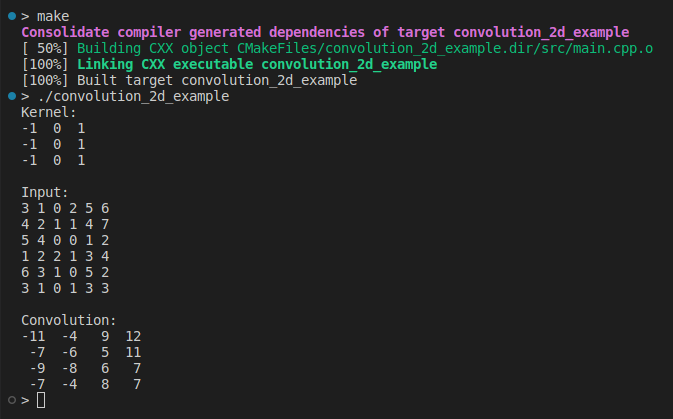
这是我们第一次实现卷积 2D,设计为易于理解。有一段时间,我们不关心性能或输入验证。让我们继续前进以获得更多见解。
在接下来的故事中,我们将学习如何使用快速傅立叶变换和托普利兹矩阵来实现卷积。
五、填充
在前面的示例中,我们注意到输出矩阵始终小于输入矩阵。有时,这种减少是好的,有时是坏的。我们可以通过在输入矩阵周围添加填充来避免这种减少:

填充为 1 的输入图像
卷积中填充的结果如下所示:
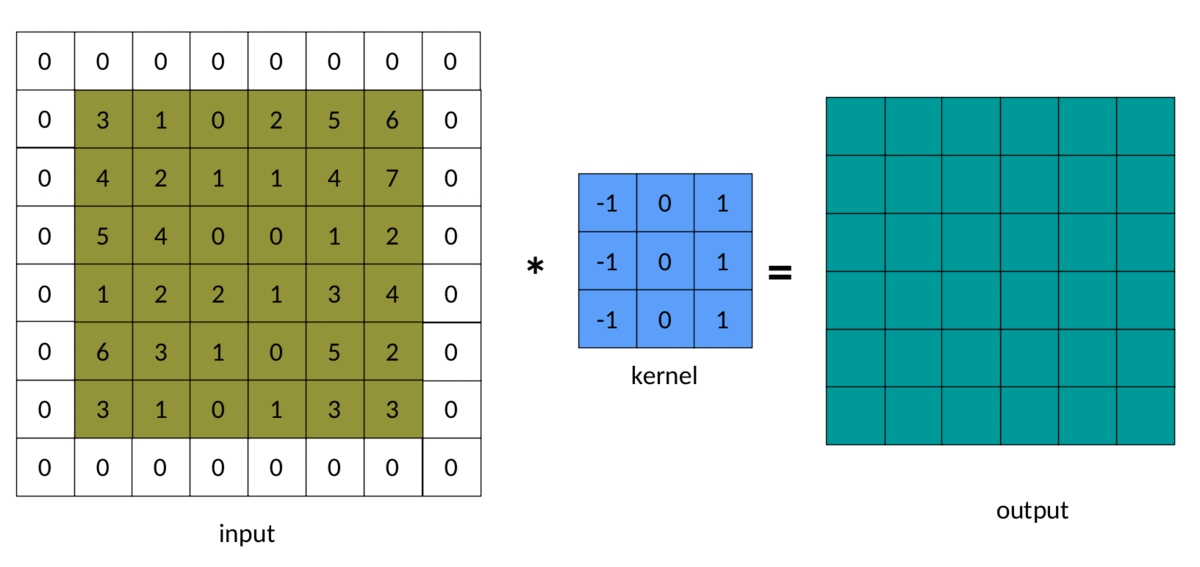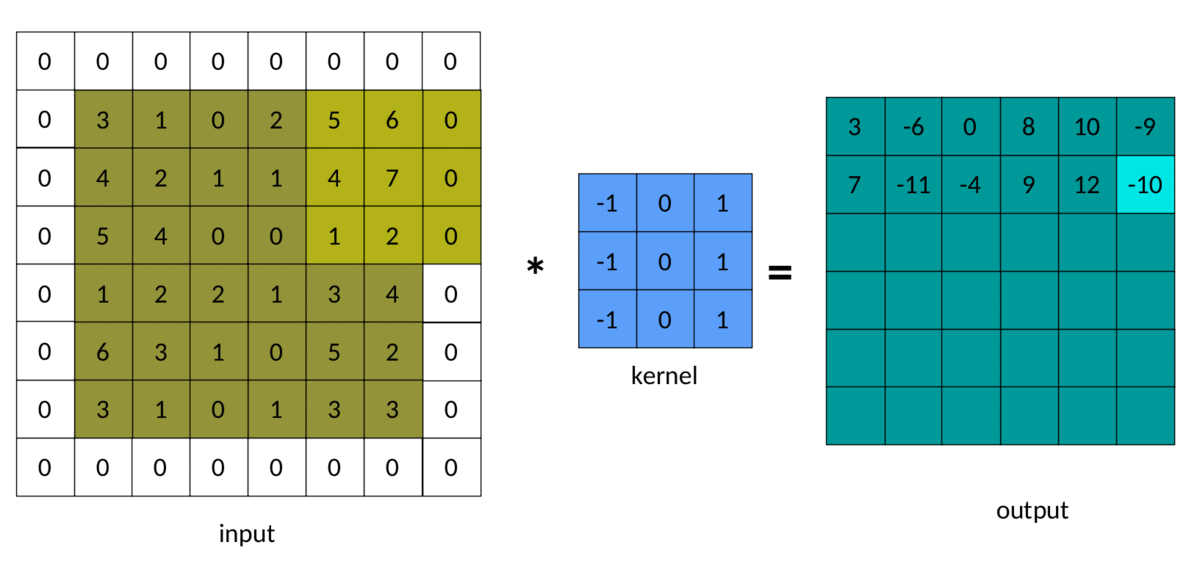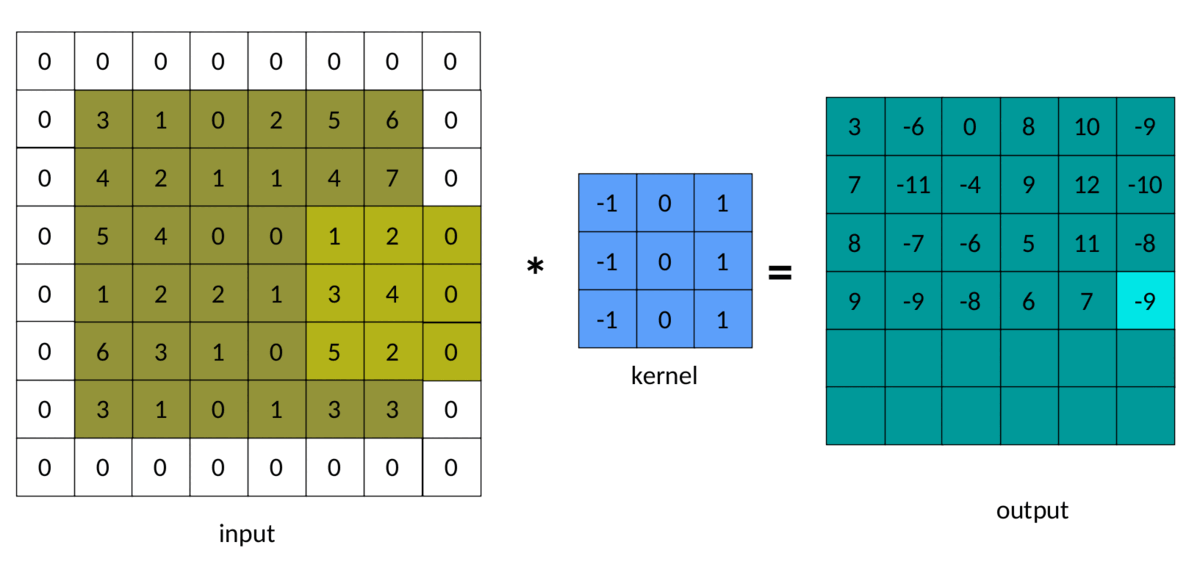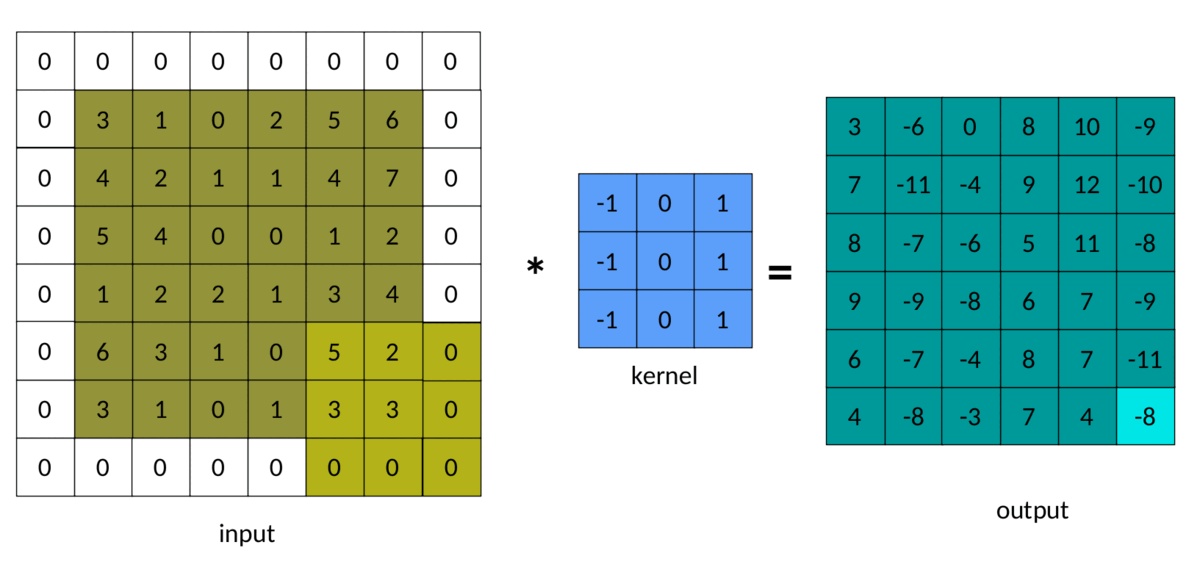
填充卷积 — 作者图片
实现填充卷积的一种简单(和蛮力)方法如下:
auto Convolution2D = [](const Matrix &input, const Matrix &kernel, int padding)
{int kernel_rows = kernel.rows();int kernel_cols = kernel.cols();int rows = input.rows() - kernel_rows + 2*padding + 1;int cols = input.cols() - kernel_cols + 2*padding + 1;Matrix padded = Matrix::Zero(input.rows() + 2*padding, input.cols() + 2*padding);padded.block(padding, padding, input.rows(), input.cols()) = input;Matrix result = Matrix::Zero(rows, cols);for(int i = 0; i < rows; ++i) {for(int j = 0; j < cols; ++j) {double sum = padded.block(i, j, kernel_rows, kernel_cols).cwiseProduct(kernel).sum();result(i, j) = sum;}}return result;
};此代码很简单,但在内存使用方面非常昂贵。请注意,我们正在制作输入矩阵的完整副本以创建填充版本:
Matrix padded = Matrix::Zero(input.rows() + 2*padding, input.cols() + 2*padding);
padded.block(padding, padding, input.rows(), input.cols()) = input;更好的解决方案可以使用指针来控制切片和内核边界:
auto Convolution2D_v2 = [](const Matrix &input, const Matrix &kernel, int padding)
{const int input_rows = input.rows();const int input_cols = input.cols();const int kernel_rows = kernel.rows();const int kernel_cols = kernel.cols();if (input_rows < kernel_rows) throw std::invalid_argument("The input has less rows than the kernel");if (input_cols < kernel_cols) throw std::invalid_argument("The input has less columns than the kernel");const int rows = input_rows - kernel_rows + 2*padding + 1;const int cols = input_cols - kernel_cols + 2*padding + 1;Matrix result = Matrix::Zero(rows, cols);auto fit_dims = [&padding](int pos, int k, int length) {int input = pos - padding;int kernel = 0;int size = k;if (input < 0) {kernel = -input;size += input;input = 0;}if (input + size > length) {size = length - input;}return std::make_tuple(input, kernel, size);};for(int i = 0; i < rows; ++i) {const auto [input_i, kernel_i, size_i] = fit_dims(i, kernel_rows, input_rows);for(int j = 0; size_i > 0 && j < cols; ++j) {const auto [input_j, kernel_j, size_j] = fit_dims(j, kernel_cols, input_cols);if (size_j > 0) {auto input_tile = input.block(input_i, input_j, size_i, size_j);auto input_kernel = kernel.block(kernel_i, kernel_j, size_i, size_j);result(i, j) = input_tile.cwiseProduct(input_kernel).sum();}}}return result;
}; 这个新代码要好得多,因为这里我们没有分配一个临时内存来保存填充的输入。但是,它仍然可以改进。调用和内存成本也很高。input.block(…)kernel.block(…)
调用的一种解决方案是使用 CwiseNullaryOp 替换它们。
block(…)
我们可以通过以下方式运行填充卷积:
#include <iostream>#include <Eigen/Core>
using Matrix = Eigen::MatrixXd;
auto Convolution2D = ...; // or Convolution2D_v2int main(int, char **)
{Matrix kernel(3, 3);kernel << -1, 0, 1,-1, 0, 1,-1, 0, 1;std::cout << "Kernel:\n" << kernel << "\n\n";Matrix input(6, 6);input << 3, 1, 0, 2, 5, 6,4, 2, 1, 1, 4, 7,5, 4, 0, 0, 1, 2,1, 2, 2, 1, 3, 4,6, 3, 1, 0, 5, 2,3, 1, 0, 1, 3, 3;std::cout << "Input:\n" << input << "\n\n";const int padding = 1;auto output = Convolution2D(input, kernel, padding);std::cout << "Convolution:\n" << output << "\n";return 0;
}
请注意,现在,输入和输出矩阵具有相同的维度。因此,它被称为填充。默认填充模式,即无填充,通常称为填充。我们的代码允许 ,或任何非负填充。samevalidsamevalid
六、内核
在深度学习模型中,核通常是奇次矩阵,如、等。有些内核非常有名,比如 Sobel 的过滤器:3x35x511x11
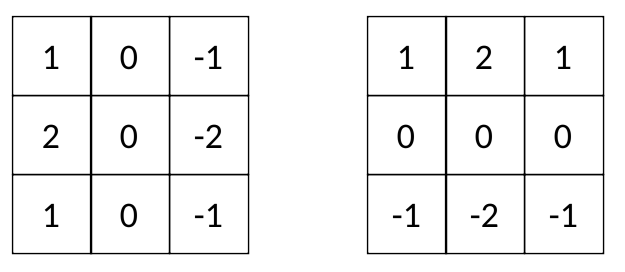
更容易看到每个 Sobel 滤镜对图像的影响:

使用 Sobel 过滤器的代码在这里。
Gy 突出显示水平边缘,Gx 突出显示垂直边缘。因此,Sobel 内核 Gx 和 Gy 通常被称为“边缘检测器”。
边缘是图像的原始特征,例如纹理、亮度、颜色等。现代计算机视觉的关键点是使用算法直接从数据中自动查找内核,例如Sobel过滤器。或者,使用更好的术语,通过迭代训练过程拟合内核。
事实证明,训练过程教会计算机程序实现如何执行复杂的任务,例如识别和检测物体、理解自然语言等......内核的训练将在下一个故事中介绍。
七、结论和下一步
在这个故事中,我们编写了第一个2D卷积,并使用Sobel滤波器作为将此卷积应用于图像的说明性案例。卷积在深度学习中起着核心作用。它们被大量用于当今每个现实世界的机器学习模型中。我们将重新审视卷积,以学习如何改进我们的实现,并涵盖一些功能,如步幅。
在下一个故事中,我们将讨论机器学习中最核心的问题:成本函数。
引用
用于深度学习的卷积算法指南
深度学习之书,古德费罗
神经网络和深度学习:教科书,Aggarwal
计算机视觉:算法和应用,Szeliski。
信号和系统,罗伯茨
相关文章:

现代C++中的从头开始深度学习:【5/8】卷积
一、说明 在上一个故事中,我们介绍了机器学习的一些最相关的编码方面,例如 functional 规划、矢量化和线性代数规划。 现在,让我们通过使用 2D 卷积实现实际编码深度学习模型来开始我们的道路。让我们开始吧。 二、关于本系列 我们将学习如何…...
以太网帧格式与吞吐量计算
以太网帧结构 帧大小的定义 以太网单个最大帧 6(目的MAC地址) 6(源MAC地址) 2(帧类型) 1500{IP数据包[IP头(20)DATA(1480)]} 4(CRC校验ÿ…...

vue中install方法
1:语法 vue提供install可供我们开发新的插件及全局注册组件等 install方法第一个参数是vue的构造器,第二个参数是可选的选项对象 export default {install(Vue,option){组件指令混入挂载vue原型} }2:注册组件 一:注册单个组件 1…...

Flutter:文件读取—— video_player、chewie、image_picker、file_picker
前言 简单学习一下几个比较好用的文件读取库 video_player 简介 用于视频播放 官方文档 https://pub-web.flutter-io.cn/packages/video_player 安装 flutter pub add video_player加载网络视频 class _MyHomePageState extends State<MyHomePage> {// 控制器late…...

vim的使用
vim文本编辑器 vim介绍命令模式光标移动选中内容复制内容粘贴内容删除撤销/恢复字符转换 编辑模式末行模式保存/退出查找行号显示文件切换 扩展 vim介绍 vim是Linux自带的文本编辑器,具有命令模式、编辑模式、末行模式三种模式。 模式间的切换: 命令模…...
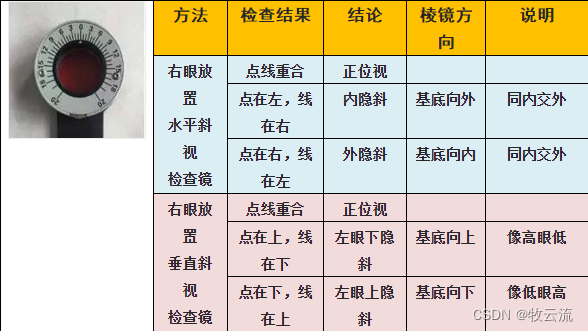
马氏杆法检查斜视
使用 检查水平向斜视时,使用水平向马氏杆检查;重直向斜视时,使用重直问马氏杆;检查旋转斜视时,使用双马氏杆. 检查水平向斜视 双眼屈光不正全矫 双眼同时打开,右眼前加水平向马氏杆,左眼前不加 双眼同时观察点光源&…...
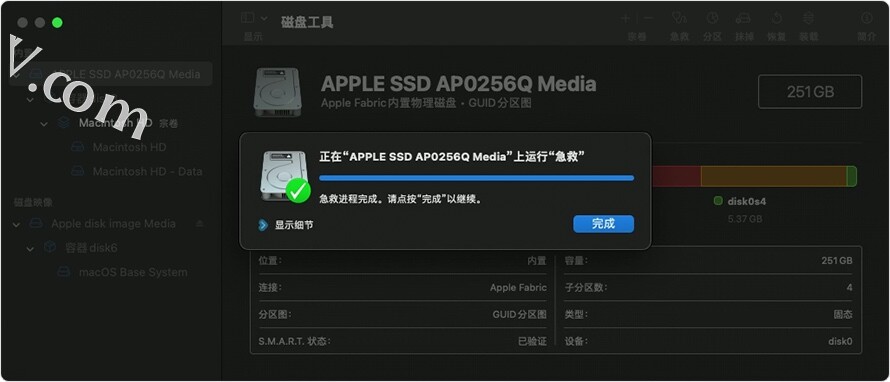
Mac电脑怎么使用“磁盘工具”修复磁盘
我们可以使用“磁盘工具”的“急救”功能来查找和修复磁盘错误。 “磁盘工具”可以查找和修复与 Mac 磁盘的格式及目录结构有关的错误。使用 Mac 时,错误可能会导致意外行为,而重大错误甚至可能会导致 Mac 彻底无法启动。 继续之前,请确保您…...
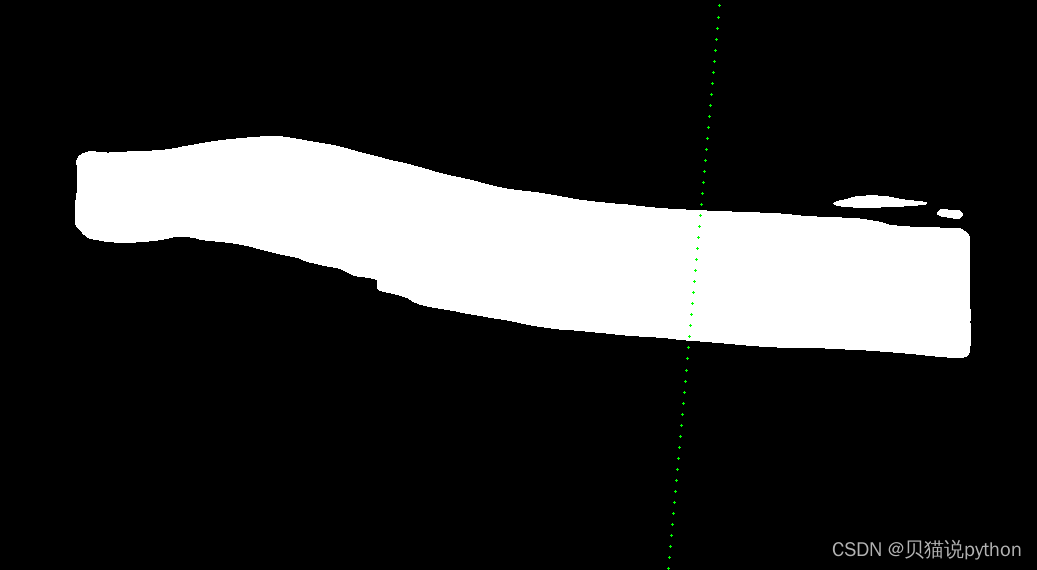
c++画出分割图像,水平线和垂直线
1、pca 找到图像某个区域的垂直线,并画出来 // 1、 斑块的框 血管二值化图,pca 找到垂直血管壁的直线, 还是根据斑块找主轴方向吧// Step 1: 提取斑块左右范围内的血管像素点坐标,std::vector<cv::Point> points;for (int y 0; y <…...
—— enumerate() 函数的用法)
Python 程序设计入门(015)—— enumerate() 函数的用法
Python 程序设计入门(015)—— enumerate() 函数的用法 目录 Python 程序设计入门(015)—— enumerate() 函数的用法一、enumerate() 函数的语法二、为可迭代对象创建索引三、将字符串、列表等转换为字典1、将字符串转换为字典2、…...

__dict__属性
__dict__ 是 Python 中的一个特殊属性,通常存在于大多数 Python 对象中,用于存储该对象的可变属性。 以下是关于 __dict__ 的一些关键点和详细信息: 存储属性:对于大多数自定义的 Python 对象,__dict__ 属性包含了这个…...
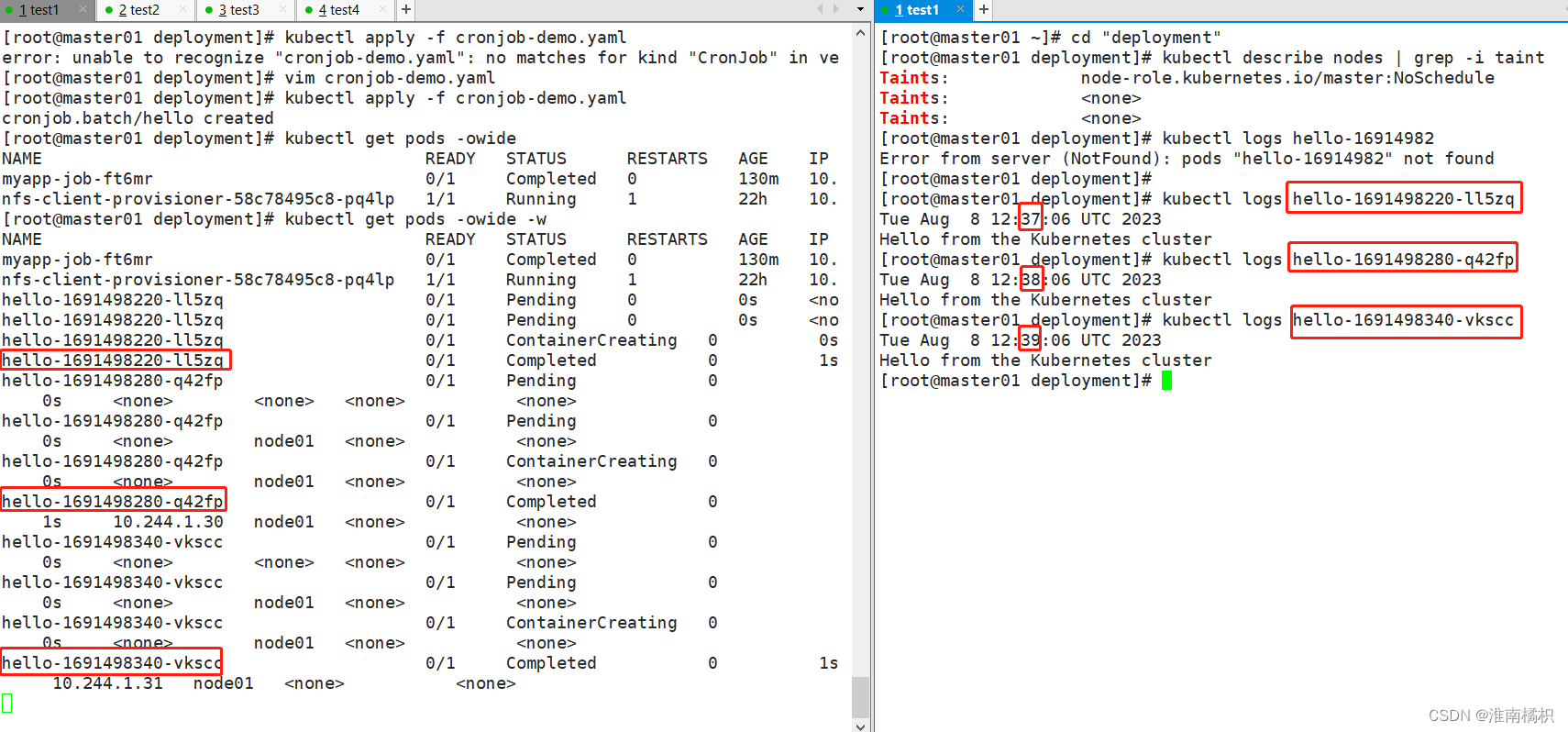
k8s之Pod控制器
目录 一、Pod控制器及其功用二、pod控制器的多种类型2.1 pod容器中的有状态和无状态的区别 三、Deployment 控制器四、SatefulSet 控制器4.1 StatefulSet由以下几个部分组成4.2 为什么要有headless?4.3 为什么要有volumeClaimTemplate?4.4 滚动更新4.5 扩…...
)
逆元(求乘法逆元的几种方法)
目录 逆元 加法逆元 乘法逆元 如何求 快速幂 扩展欧几里得 O(n)求1到n的乘法逆元 逆元 数学中,逆元素(英语:Inverse element)推广了加法中的加法逆元和乘法中的倒数。直观地说,它是一个可以取消另一给定元素运…...

没点本事,还真做不好数字化转型
数字化转型逐渐成为企业业务增长的利器 然而,在此过程中 企业最应该注重哪些? 效率?质量? 但还有一个至关重要的点不容忽视 那就是安全 有一家硬核企业通过技术与狠活 硬生生提升了应用安全性 保障了产业与数字化的安全融合…...
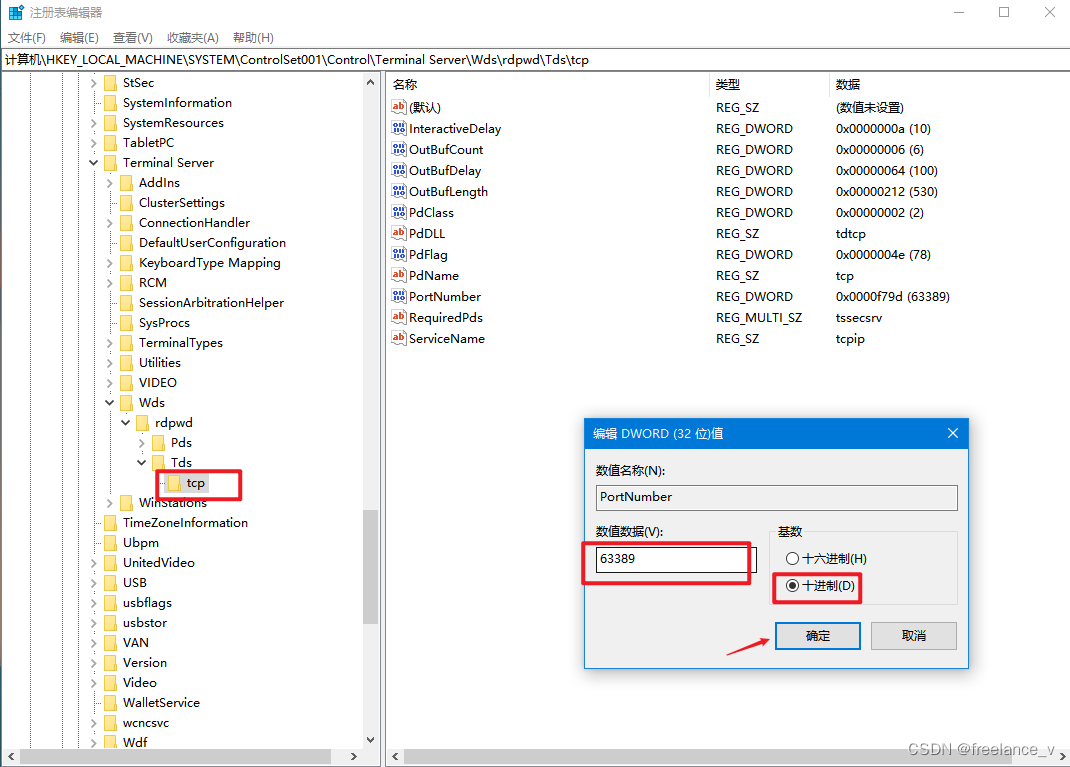
windows 10 远程桌面配置
1. 修改远程桌面端口(3389) 打开注册表(winr), 输入regedit 找到配置项【计算机\HKEY_LOCAL_MACHINE\SYSTEM\ControlSet001\Control\Terminal Server\Wds\rdpwd\Tds\tcp】 , 可以通过搜索“Wds”快速定位。 修改端口配…...

OpenStreetMap 上基于A*搜索算法的C ++路线规划项目
引言 在现代的地理信息系统(GIS)中,路线规划是一个重要的组成部分。它涉及到从一个地点到另一个地点的最优路径的确定。在这篇文章中,我们将探讨如何在OpenStreetMap数据上实现一个基于A*搜索算法的C路线规划项目。 OpenStreetM…...
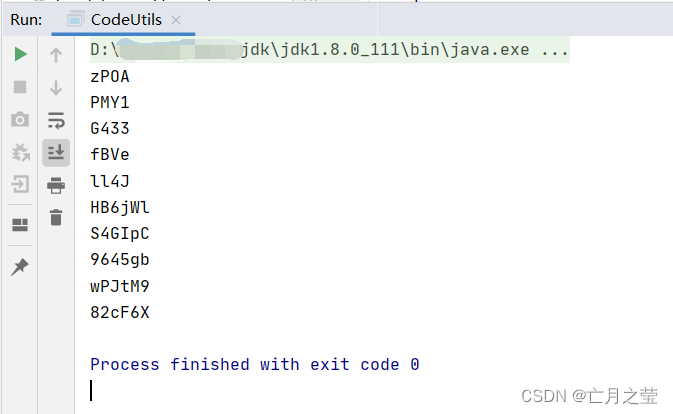
java实现随机生成验证码
import java.util.concurrent.ThreadLocalRandom;/* 生成验证码的工具 可动态配置验证码长度*/ public class CodeUtils {public static void main(String[] args) {//随机生成5个长度为4的验证码for (int i 0; i < 5; i) {System.out.println(CodeUtils.getCode(4));}for …...
Positive证书是什么?
Positive SSL是全球著名CA Sectigo的子品牌, 也是目前全球签发量最高的商业SSL证书。价格低,安全性高,在个人网站和中小型企业网站中拥有极高的占有率。 Positive SSL证书包括DV SSL, EV SSL,也是唯一支持IP地址加密的…...

vulnhub靶场-y0usef笔记
vulnhub靶场-y0usef笔记 信息收集 首先fscan找到目标机器ip http://192.168.167.70/ nmap扫描端口 Host is up (0.00029s latency). Not shown: 998 closed tcp ports (reset) PORT STATE SERVICE VERSION 22/tcp open ssh OpenSSH 6.6.1p1 Ubuntu 2ubuntu2.13 (Ub…...
华为智选首款纯电轿跑“LUXEED”能大卖吗?
监制 | 何玺 排版 | 叶媛 华为智选纯电轿跑来袭! 8月7日,华为常务董事余承东在社交媒体上发文,宣布华为智选即将推出首款“突破想象”的纯电轿跑车。 01 华为智选首款纯电轿跑来袭 余承东的发文引起了极大关注,在各大媒体的报…...

ArcGIS API for JavaScript 3.44 地图Demo示例合集
ArcGIS API for JavaScript 3.44 demo合集 (一)创建地图(二)基准图库(三)编辑书签(四)主页按钮(五)LayerList小部件(六)测量小工具&am…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

SQL注入篇-sqlmap的配置和使用
在之前的皮卡丘靶场第五期SQL注入的内容中我们谈到了sqlmap,但是由于很多朋友看不了解命令行格式,所以是纯手动获取数据库信息的 接下来我们就用sqlmap来进行皮卡丘靶场的sql注入学习,链接:https://wwhc.lanzoue.com/ifJY32ybh6vc…...
