逆元(求乘法逆元的几种方法)
目录
逆元
加法逆元
乘法逆元
如何求
快速幂
扩展欧几里得
O(n)求1到n的乘法逆元
逆元
数学中,逆元素(英语:Inverse element)推广了加法中的加法逆元和乘法中的倒数。直观地说,它是一个可以取消另一给定元素运算的元素。
加法逆元
对于一个任意数n,存在加法逆元(英语:Additive Inverse,又称相反数),其与nn的和为零(加法单位元)。n的加法逆元表示为-n。
乘法逆元
数学上,一个数xx的倒数(reciprocal),或称乘法逆元(multiplicative inverse),是指一个与x相乘的积为1的数。显然在实数范围内x的乘法逆元是1/x。
信息学中常用的乘法逆元是模逆元。
一整数a对同余n之模逆元是指满足以下公式的整数b
a b ≡ 1 (mod n).
整数a对模数n之模逆元存在的充分必要条件是a和n互素,若此模逆元存在,在模数n 下的除法可以用和对应模逆元的乘法来达成,此概念和实数除法的概念相同。
如何求
快速幂
对于质数pp,考虑费马小定理a^(p−1) mod p = 1,可以得到ii的逆元是pow(i, p - 2, p)。
对于合数pp,考虑欧拉定理a^(φ(p) ) mod p = 1,可以得到ii的逆元是pow(i, phi(p) - 1, p)。
但是因为对于一般的数字计算φ(p)复杂度较高,并不使用这个方法。
扩展欧几里得
因为快速幂非常好写,一般只有在模非质数,或者是卡常数的情况下使用这个算法。
解出ax+py=1的一组解(x,y),x就是a关于模n的其中一个模逆元。
需要注意求解出的xx可能是负数。
O(n)求1到n的乘法逆元
inv[1] = 1;
for (int i = 2; i <= n; i++) {inv[i] = (long long)inv[p % i] * (p - p / i) % p;
}
这个方法可以用于组合数的预处理。
这个方法还可以改写为递归版,以替代质数情况下用快速幂求逆元。
int inv(int x) {if (x == 1) {return 1;} else {return (long long)inv(p % i) * (p - p / i) % p;}
}
另一个常用与组合数预处理的做法是:
先预处理出1到n的阶乘,然后计算n阶乘的逆元,然后倒序推出n到1阶乘的逆元。
fac[0] = 1;
for (int i = 1; i <= n; i++) {fac[i] = (long long)fac[i - 1] * i % p;
}
invfac[n] = pow(fac[n], p - 2, p);
for (int i = n - 1; i >= 0; i--) {invfac[i] = (long long)invfac[i + 1] * (i + 1) % p;
}相关文章:
)
逆元(求乘法逆元的几种方法)
目录 逆元 加法逆元 乘法逆元 如何求 快速幂 扩展欧几里得 O(n)求1到n的乘法逆元 逆元 数学中,逆元素(英语:Inverse element)推广了加法中的加法逆元和乘法中的倒数。直观地说,它是一个可以取消另一给定元素运…...

没点本事,还真做不好数字化转型
数字化转型逐渐成为企业业务增长的利器 然而,在此过程中 企业最应该注重哪些? 效率?质量? 但还有一个至关重要的点不容忽视 那就是安全 有一家硬核企业通过技术与狠活 硬生生提升了应用安全性 保障了产业与数字化的安全融合…...
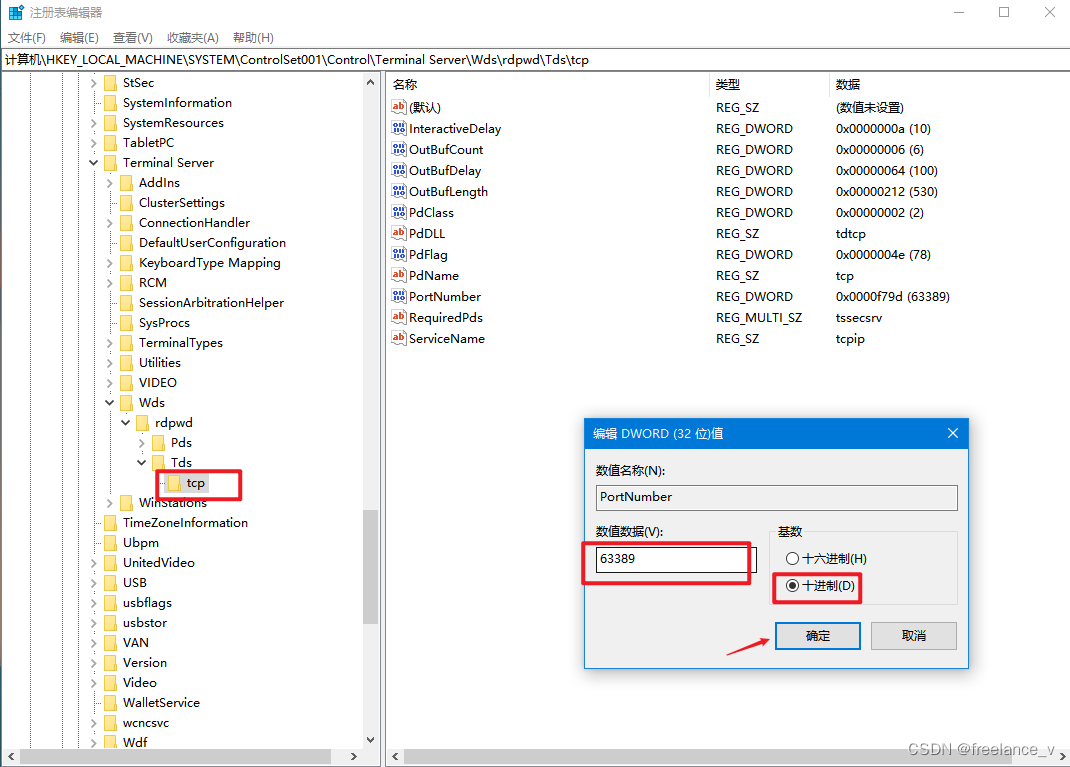
windows 10 远程桌面配置
1. 修改远程桌面端口(3389) 打开注册表(winr), 输入regedit 找到配置项【计算机\HKEY_LOCAL_MACHINE\SYSTEM\ControlSet001\Control\Terminal Server\Wds\rdpwd\Tds\tcp】 , 可以通过搜索“Wds”快速定位。 修改端口配…...

OpenStreetMap 上基于A*搜索算法的C ++路线规划项目
引言 在现代的地理信息系统(GIS)中,路线规划是一个重要的组成部分。它涉及到从一个地点到另一个地点的最优路径的确定。在这篇文章中,我们将探讨如何在OpenStreetMap数据上实现一个基于A*搜索算法的C路线规划项目。 OpenStreetM…...
java实现随机生成验证码
import java.util.concurrent.ThreadLocalRandom;/* 生成验证码的工具 可动态配置验证码长度*/ public class CodeUtils {public static void main(String[] args) {//随机生成5个长度为4的验证码for (int i 0; i < 5; i) {System.out.println(CodeUtils.getCode(4));}for …...
Positive证书是什么?
Positive SSL是全球著名CA Sectigo的子品牌, 也是目前全球签发量最高的商业SSL证书。价格低,安全性高,在个人网站和中小型企业网站中拥有极高的占有率。 Positive SSL证书包括DV SSL, EV SSL,也是唯一支持IP地址加密的…...

vulnhub靶场-y0usef笔记
vulnhub靶场-y0usef笔记 信息收集 首先fscan找到目标机器ip http://192.168.167.70/ nmap扫描端口 Host is up (0.00029s latency). Not shown: 998 closed tcp ports (reset) PORT STATE SERVICE VERSION 22/tcp open ssh OpenSSH 6.6.1p1 Ubuntu 2ubuntu2.13 (Ub…...
华为智选首款纯电轿跑“LUXEED”能大卖吗?
监制 | 何玺 排版 | 叶媛 华为智选纯电轿跑来袭! 8月7日,华为常务董事余承东在社交媒体上发文,宣布华为智选即将推出首款“突破想象”的纯电轿跑车。 01 华为智选首款纯电轿跑来袭 余承东的发文引起了极大关注,在各大媒体的报…...

ArcGIS API for JavaScript 3.44 地图Demo示例合集
ArcGIS API for JavaScript 3.44 demo合集 (一)创建地图(二)基准图库(三)编辑书签(四)主页按钮(五)LayerList小部件(六)测量小工具&am…...

RFID工业识别技术:供应链智能化的科技颠覆
RFID工业识别技术,作为物联网的先锋,正在供应链管理领域展现着前所未有的科技颠覆。从物料追踪到库存管理,再到物流配送,RFID技术以其高效的数据采集和智能的自动化处理,彻底改变着传统供应链的运营方式。 RFID在物料追…...

行列转换两例的思考
1、多行转成一列 (1)、建测试表及插入测试数据 create table t(i int,a varchar2(1)); insert into t(i,a) select 1,a from dual union all select 1,b from dual union all select 1,d from dual union all select 1,e from dual union all select 2,z from dual union all…...
高德地图 SDK 接口测试接入(AndroidTest 上手)
学习资料 官方文档 在 Android 平台上测试应用 | Android 开发者 | Android Developers 测试了解 【玩转Test】开篇-Android test 介绍 Android单元测试全解_android 单元测试_一代小强的博客-CSDN博客 Android单元测试-对Activity的测试_activitytestrule_许佳佳233的博客…...
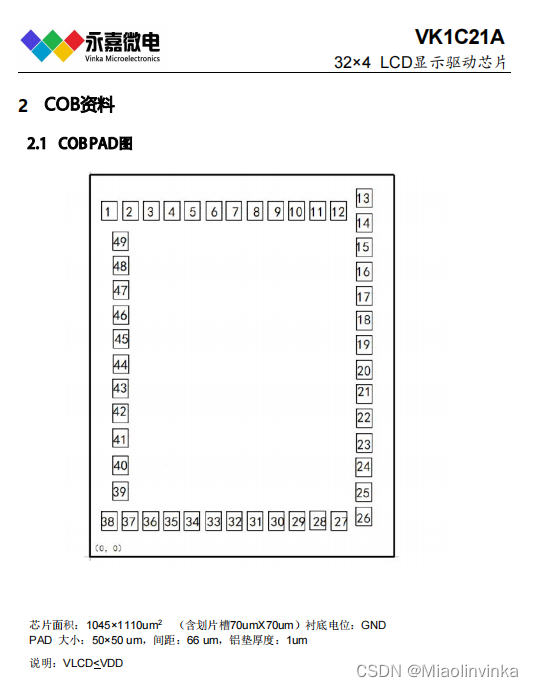
省电模式稳定电压显示IC32×4 LCD显示驱动芯片
简述 VK1C21A是一个点阵式存储映射的LCD驱动器,可支持最大128点(32SEGx4COM) 的LCD屏,也支持2COM和3COM的LCD屏。单片机可通过3/4个通信脚配置显示参数和发 送显示数据,也可通过指令进入省电模式。具备高抗干扰&a…...

分布式架构的观测
分布式架构的观测 日志日志的输出收集与缓冲加工与聚合存储与查询 追踪数据收集 度量 在一个分布式应用中,如果出现了某个异常,那我们必然不可能只依靠 awk、grep 等命令来查看日志分析问题,往往分布式架构的一个异常都贯通多个节点ÿ…...

交替方向乘子
目录 一,交替方向乘子ADMM 1,带线性约束的分离优化模型 2,常见优化模型转带线性约束的分离优化模型 3,带线性约束的分离优化模型求解 4,交替方向乘子ADMM 本文部分内容来自教材 一,交替方向乘子ADMM …...
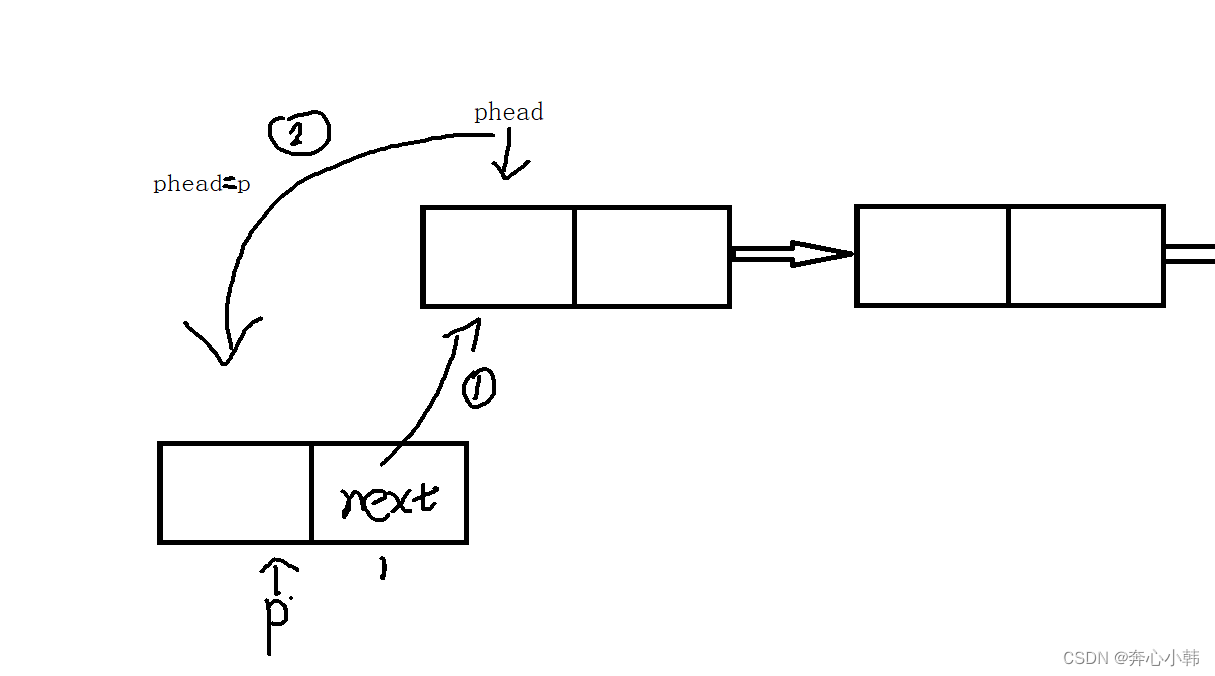
9-数据结构-栈(C语言版)
数据结构-栈(C语言版) 目录 数据结构-栈(C语言版) 1.栈的基础知识 1.入栈,出栈的排列组合 情景二:Catalan函数(计算不同出栈的总数) 2.栈的基本操作 1.顺序存储 (1)顺序栈-定义…...

C#,数值计算——用于从连续的数据值流估计任意分位数的计算方法与源程序
1 分位数Quantile 分位数(Quantile),亦称分位点,是指将一个随机变量的概率分布范围分为几个等份的数值点,常用的有中位数(即二分位数)、四分位数、百分位数等。 2 常见各类分位数 2.1 二分位…...

实践分享:小程序事件系统设计
微信小程序官方文档中解释说:事件是用于子组件向父组件传递数据,可以传递任意数据。 小程序开发中的事件是指视图层到逻辑层的通讯方式,主要是可以将用户的行为反馈到逻辑层进行处理。事件可以绑定在组件上,当达到触发事件&#…...

无涯教程-Perl - bless函数
描述 此函数告诉REF引用的实体,它现在是CLASSNAME包中的对象,如果省略CLASSNAME,则为当前包中的对象。建议使用bless的两个参数形式。 语法 以下是此函数的简单语法- bless REF, CLASSNAMEbless REF返回值 该函数返回对祝福到CLASSNAME中的对象的引用。 例 以下是显示其…...

Java关键字:final解析
目录 一、final变量 二、final方法 三、final类 final是Java语言中的一个关键字,凡是被final关键字修饰过的内容都是不可改变的。 一、final变量 final关键字可用于变量声明,一旦该变量被设定,就不可以再改变该变量的值。通常࿰…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...

HTML中各种标签的作用
一、HTML文件主要标签结构及说明 1. <!DOCTYPE html> 作用:声明文档类型,告知浏览器这是 HTML5 文档。 必须:是。 2. <html lang“zh”>. </html> 作用:包裹整个网页内容,lang"z…...

性能优化中,多面体模型基本原理
1)多面体编译技术是一种基于多面体模型的程序分析和优化技术,它将程序 中的语句实例、访问关系、依赖关系和调度等信息映射到多维空间中的几何对 象,通过对这些几何对象进行几何操作和线性代数计算来进行程序的分析和优 化。 其中࿰…...
:PyQuery 框架)
Python爬虫(四):PyQuery 框架
PyQuery 框架详解与对比 BeautifulSoup 第一部分:PyQuery 框架介绍 1. PyQuery 是什么? PyQuery 是一个 Python 的 HTML/XML 解析库,它采用了 jQuery 的语法风格,让开发者能够用类似前端 jQuery 的方式处理文档解析。它的核心特…...
