讲解密码学综合应用
密码学综合应用是指将密码学的理论和技术应用于各种场景中,以保障信息的安全性、完整性和可靠性。密码学的应用范围非常广泛,包括通信安全、网络安全、电子商务、数字签名、认证、密钥管理等。下面将简要介绍一些密码学综合应用的实例:
1. 加密通信:使用对称加密(如AES)或非对称加密(如RSA)对数据进行加密,确保在传输过程中的数据安全。例如,HTTPS协议就使用了SSL/TLS加密来保护网络传输的数据。
2. 数字签名:使用数字签名技术(如DSA、ECDSA等)对文件或数据进行签名,以验证数据的完整性和来源。例如,GPG和S/MIME协议就采用了数字签名技术来保障邮件的安全。
3. 认证和授权:利用密码学原理实现身份认证和权限控制。例如,Kerberos协议、OAuth 2.0等协议提供了认证和授权机制,用于保护系统的安全性。
4. 密钥管理:密钥管理是密码学应用中的一个重要环节。通过密钥管理系统(如KMS)对密钥进行生成、分发、存储和销毁,确保密钥的安全性。
5. 零知识证明:零知识证明是一种密码学协议,允许一方向另一方证明某个陈述是正确的,而无需透露任何其他信息。例如,Zcash和ZK-SNARKs等协议就利用了零知识证明技术来保护用户隐私。
6. 密码学应用在区块链:区块链技术中的加密算法(如SHA-256、ECC等)和共识机制(如工作量证明PoW、权益证明PoS等)都有密码学的影子,它们共同保证了区块链的安全、透明和不可篡改。
7. 隐私保护:密码学技术在隐私保护领域有广泛应用,如差分隐私、同态加密、多方计算等。这些技术在保护数据隐私的同时,允许对数据进行分析和处理。
相关文章:

讲解密码学综合应用
密码学综合应用是指将密码学的理论和技术应用于各种场景中,以保障信息的安全性、完整性和可靠性。密码学的应用范围非常广泛,包括通信安全、网络安全、电子商务、数字签名、认证、密钥管理等。下面将简要介绍一些密码学综合应用的实例: 1. 加…...

Flamingo
基于已有的图像模型和文本模型构建多模态模型。输入是图像、视频和文本,输出是文本。 Vision encoder来自预训练的NormalizerFree ResNet (NFNet),之后经过图文对比损失学习。图片经过图像模型的输出是2D grid,视频按1FPS的频率采样后经过图…...

Leetcode-每日一题【剑指 Offer 12. 矩阵中的路径】
题目 单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。 例如,在下面的 34 的矩阵中包含单词 "ABCCED"(单词中的字母…...
安全渗透知识总结二
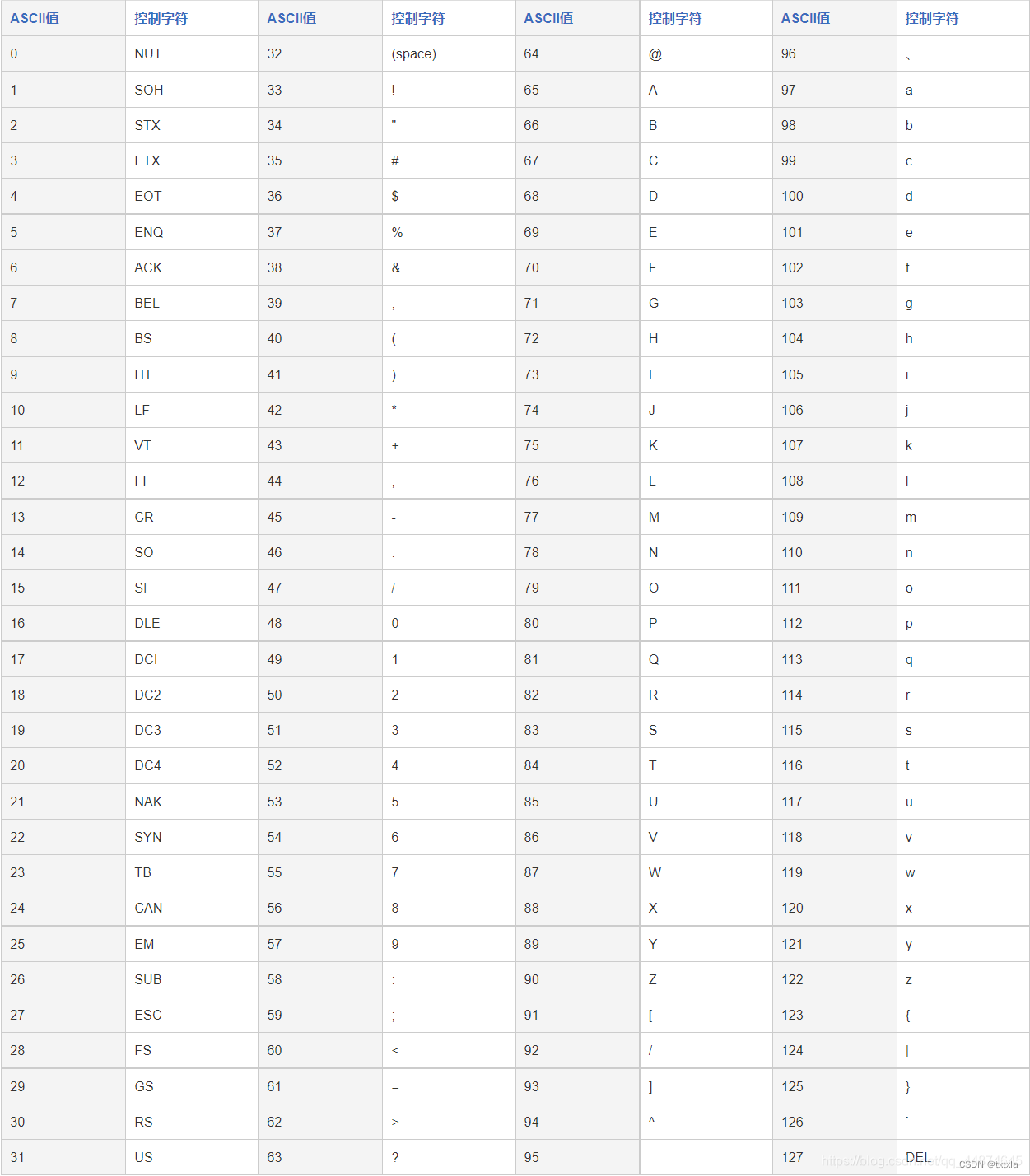
目录 一、html实体编码 1、Unicode字符编码 2、字符的数字表示 3、常见实体编码 4、url 协议 主机 http状态码 http常用的状态码 端口 常见协议端口 查询参数 锚点 url字符 urlcode字符 绝对url和相对url 二、字符编码 Ascll字符集 html字符集 html的url编码 …...
+notifyAll()实现多个线程交替遍历,输出ABCABC)
【线程】wait()+notifyAll()实现多个线程交替遍历,输出ABCABC
背景 有三个线程,每个线程分别循环输出A、B、C,各线程循环10次,要求输出结果是ABCABCABC这样的 代码 Data public class PrintThread extends Thread {private String string; // 输出的字符串private int order; …...
MyBatis 缓存机制复习及项目中的应用经历
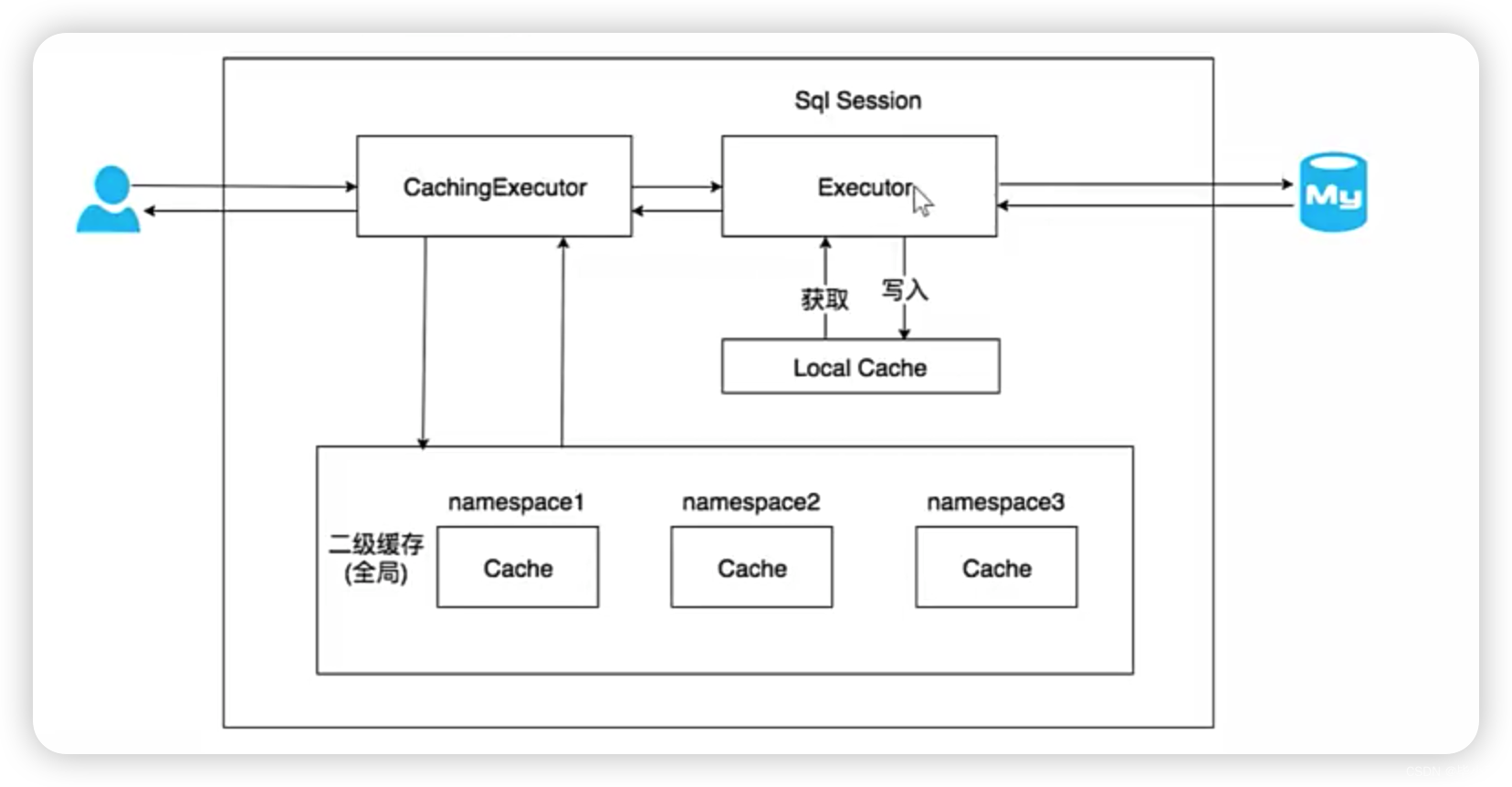
背景 想起前两年工作中因为二级缓存默认开启导致的问题,完整的看了一个介绍 MyBatis 缓存机制的视频《MyBatis 缓存基础知识讲解》。 总计知识点: 缓存的类型及开关这是个形同虚设的功能,线上环境应该禁用缓存 MyBatis 缓存分类 MyBasit…...

匈牙利算法详解
匈牙利算法(Hungarian Algorithm)是一种组合优化算法(combinatorial optimization algorithm),用于求解指派问题(assignment problem),算法时间复杂度为O(N^3)。Harold Kuhn发表于1955年,由于该算法基于两位匈牙利数学家的早期研究成果&#…...

script的三种加载模式
默认加载:阻断dom树构建(html文档解析),下载资源,然后立即执行,完毕后再进行dom树构建defer 加载:下载照旧,但执行延后。即下载资源和dom构建同时进行,但等dom树构建完再执行async:下…...

mongo 中两张表联合查询
表1:user 表 表2:dept表 需要查询user表中roleCodes 包含shr 的数据 然后联合dept表 需要部门名称 db.user.aggregate([{$match: {roleCodes: "shr" // 匹配roleCodes包含"shr"的文档}},{$lookup: {from: "dept", // 关联的集合名称loc…...

【Linux】多路转接 -- epoll
文章目录 1. 认识epoll2. epoll相关系统调用接口3. epoll工作原理4. epoll服务器5. epoll的优点6. epoll的工作方式7. epoll的使用场景 1. 认识epoll epoll系统调用和select以及poll是一样的,都是可以让我们的程序同时监视多个文件描述符上的事件是否就绪。 epoll…...
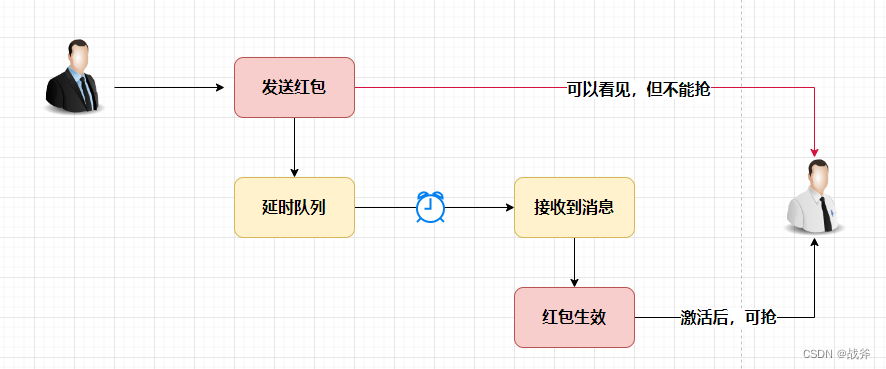
学会RabbitMQ的延迟队列,提高消息处理效率
系列文章目录 手把手教你,本地RabbitMQ服务搭建(windows) 消息队列选型——为什么选择RabbitMQ RabbitMQ灵活运用,怎么理解五种消息模型 RabbitMQ 能保证消息可靠性吗 推或拉? RabbitMQ 消费模式该如何选择 死信是什么…...
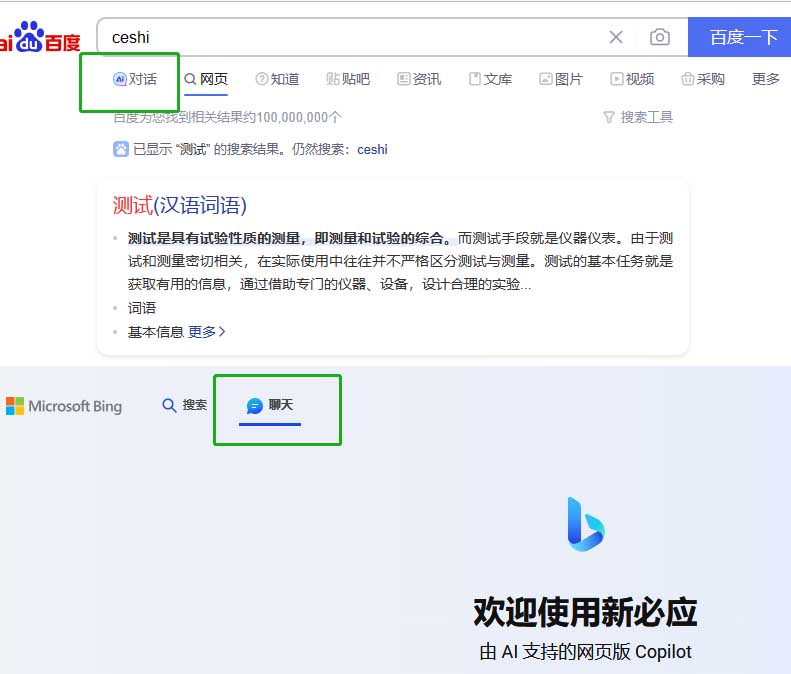
ChatGPT会取代搜索引擎吗?BingChat、GoogleBard与ChatGPT区别
目前暂时不会,ChatGPT为代表的聊天机器人很可能会直接集成到搜索中,而不是取代它。微软已经通过Bing Chat和Bing做到了这一点,它将“聊天”选项卡直接放入Bing搜索的菜单中。Google、百度也分别开始尝试通过其AI生成技术将Google Bard、文心一…...
多个QLabel中文字左右对其问题研究
众所周知,关于QLabel 中的文字对其方式,官方提供多种,具体可参考 AlignmentFlag,这里就不详细列举了。 实际开发中有这样一个需求:多个lab中,文字显示不同,长度不一,但想要实现视觉…...
链式二叉树统计结点个数的方法和bug
方法一: 分治:分而治之 int BTreeSize1(BTNode* root) {if (root NULL) return 0;else return BTreeSize(root->left)BTreeSize(root->right)1; } 方法二: 遍历计数:设置一个计数器,对二叉树正常访问&#…...
: memory corruption: 0x0000000001496d90 ***)
C语言-报错集锦-03-malloc(): memory corruption: 0x0000000001496d90 ***
一、报错信息 [2023-8]--[ Debug ]--Push Data To StAccessPath OK. [2023-8]--[ Debug ]--Judge Vertex(0) Is Not Accessed. [2023-8]--[ Debug ]--Judge Vertex(2) Is Accessed. [2023-8]--[ Debug ]--Judge Vertex(3) Is Not Accessed. [2023-8]--[ Debug ]--Judge Vertex…...

现代C++中的从头开始深度学习:【5/8】卷积
一、说明 在上一个故事中,我们介绍了机器学习的一些最相关的编码方面,例如 functional 规划、矢量化和线性代数规划。 现在,让我们通过使用 2D 卷积实现实际编码深度学习模型来开始我们的道路。让我们开始吧。 二、关于本系列 我们将学习如何…...
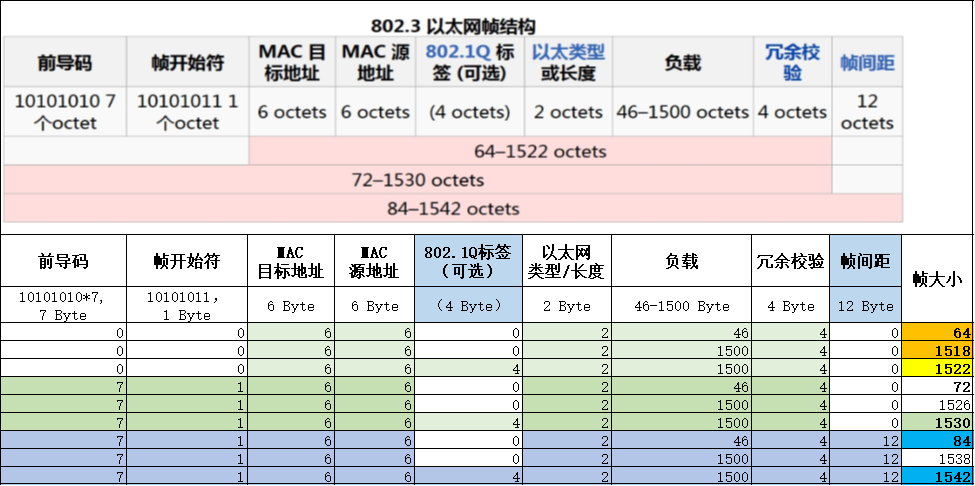
以太网帧格式与吞吐量计算
以太网帧结构 帧大小的定义 以太网单个最大帧 6(目的MAC地址) 6(源MAC地址) 2(帧类型) 1500{IP数据包[IP头(20)DATA(1480)]} 4(CRC校验ÿ…...

vue中install方法
1:语法 vue提供install可供我们开发新的插件及全局注册组件等 install方法第一个参数是vue的构造器,第二个参数是可选的选项对象 export default {install(Vue,option){组件指令混入挂载vue原型} }2:注册组件 一:注册单个组件 1…...

Flutter:文件读取—— video_player、chewie、image_picker、file_picker
前言 简单学习一下几个比较好用的文件读取库 video_player 简介 用于视频播放 官方文档 https://pub-web.flutter-io.cn/packages/video_player 安装 flutter pub add video_player加载网络视频 class _MyHomePageState extends State<MyHomePage> {// 控制器late…...

vim的使用
vim文本编辑器 vim介绍命令模式光标移动选中内容复制内容粘贴内容删除撤销/恢复字符转换 编辑模式末行模式保存/退出查找行号显示文件切换 扩展 vim介绍 vim是Linux自带的文本编辑器,具有命令模式、编辑模式、末行模式三种模式。 模式间的切换: 命令模…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...
