vuejs 设计与实现 - 简单diff算法
DOM 复用与key的作用:
DOM 复用什么时候可复用?
- key 属性就像虚拟节点的“身份证”号,只要两个虚拟节点的 type属性值和 key 属性值都相同,那么我们就认为它们是相同的,即可以进行 DOM 的复用。即 我们通过【移动】来操作dom,而不是删除dom,创建dom。这样会更节省性能。
如下图展示了有key和无key时新旧两组子节点的映射情况:
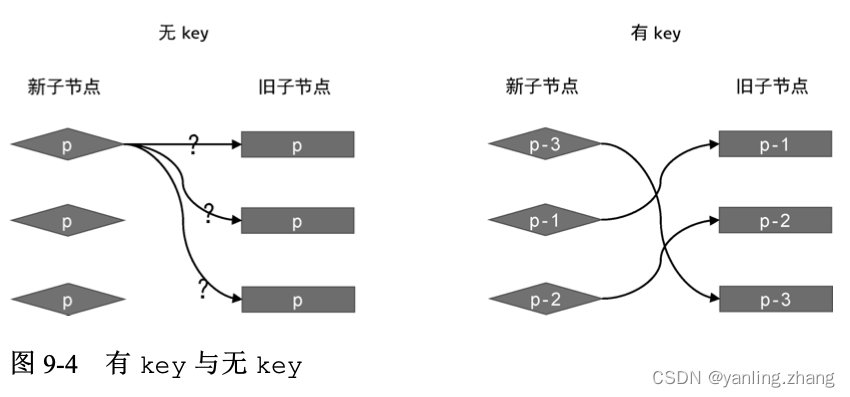
如上图可知:如果没有 key,我们无法知道新子节点与旧子节点 间的映射关系,也就无法知道应该如何移动节点。有 key 的话情况则 不同,我们根据子节点的 key 属性,能够明确知道新子节点在旧子节 点中的位置,这样就可以进行相应的 DOM 移动操作了。
强调:DOM 可复用并不意味着不需要更新.如下所示的2个虚拟节点:
const oldVNode = { type: 'p', key: 1, children: 'text 1' }
const newVNode = { type: 'p', key: 1, children: 'text 2' }
这两个虚拟节点拥有相同的 key 值和 vnode.type 属性值。这意 味着, 在更新时可以复用 DOM 元素,即只需要通过移动操作来完成更 新。但仍需要对这两个虚拟节点进行打补丁操作,因为新的虚拟节点 (newVNode)的文本子节点的内容已经改变了(由’text 1’变成 ‘text 2’)。因此,在讨论如何移动DOM之前,我们需要先完成打补丁操作.
本节以下面的节点为例,进行简单diff算法:
const oldVNode = {type: 'div',children: [{ key: 1, type: 'p', children: '1' },{ key: 2, type: 'p', children: '2' },{ key: 3, type: 'p', children: '3' },]}const newVNode = {type: 'div',children: [{ key: 3, type: 'p', children: '3' },{ key: 2, type: 'p', children: '2' },{ key: 1, type: 'p', children: '1' },]}
每一次寻找可复用的节点时,都会记录该可复用 节点在旧的一组子节点中的位置索引。
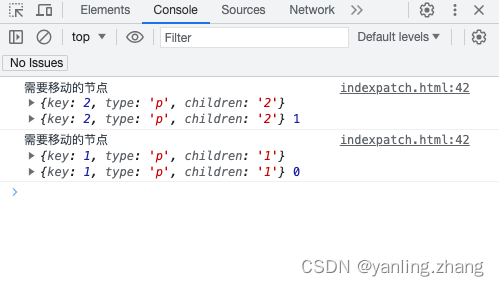
找到需要移动的元素
// 1.找到需要移动的元素
function patchChildren(n1, n2) {const oldChildren = n1.childrenconst newChildren = n2.childrenlet lastIndex = 0for (let i = 0; i < newChildren.length; i++) {const newVNode = newChildren[i]for (j = 0; j < oldChildren.length; j++) {const oldVNode = oldChildren[j]if (newVNode.key === oldVNode.key) {// 移动DOM之前,我们需要先完成打补丁操作patch(oldVNode, newVNode, container)if (j < lastIndex) {console.log('需要移动的节点', newVNode, oldVNode, j)} else {lastIndex = j}break;}}}
}
patchChildren(oldVNode, newVNode)
如何移动元素
更新的过程:
第一步:取新的一组子节点中第一个节点 p-3,它的 key 为 3,尝试在旧的一组子节点中找到具有相同 key 值的可复用节点。发现能够找到,并且该节点在旧的一组子节点中的索引为 2。此时变量 lastIndex 的值为 0,索引 2 不小于 0,所以节点 p-3 对应的真实 DOM 不需要移动,但需要更新变量 lastIndex 的值为2。
第二步:取新的一组子节点中第二个节点 p-1,它的 key 为 1,尝试在旧的一组子节点中找到具有相同 key 值的可复用节点。发
现能够找到,并且该节点在旧的一组子节点中的索引为 0。此时变量 lastIndex 的值为 2,索引 0 小于 2,所以节点 p-1 对应的真实 DOM 需要移动。
到了这一步,我们发现,节点 p-1 对应的真实 DOM 需要移动,但应该移动到哪里呢?我们知道, children的顺序其实就是更新后真实DOM节点应有的顺序。所以p-1在新children 中的位置就代表了真实 DOM 更新后的位置。由于节点p-1在新children中排在节点p-3后面,所以我们应该把节点p-1 所对应的真实DOM移到节点p-3所对应的真实DOM后面。
可以看到,这样操作之后,此时真实 DOM 的顺序为 p-2、p-3、p-1。
第三步:取新的一组子节点中第三个节点 p-2,它的 key 为 2。尝试在旧的一组子节点中找到具有相同 key 值的可复用节点。发现能够找到,并且该节点在旧的一组子节点中的索引为 1。此时变量 lastIndex 的值为 2,索引 1 小于 2,所以节点 p-2 对应的真实 DOM 需要移动。
如下图移动节点:

第三步与第二步类似,节点 p-2 对应的真实 DOM 也需要移动。 面后同样,由于节点 p-2 在新 children 中排在节点 p-1 后面,所以我们应该把节点 p-2 对应的真实 DOM 移动到节点 p-1 对应的真实DOM 后面。移动后的结果如图下图所示:
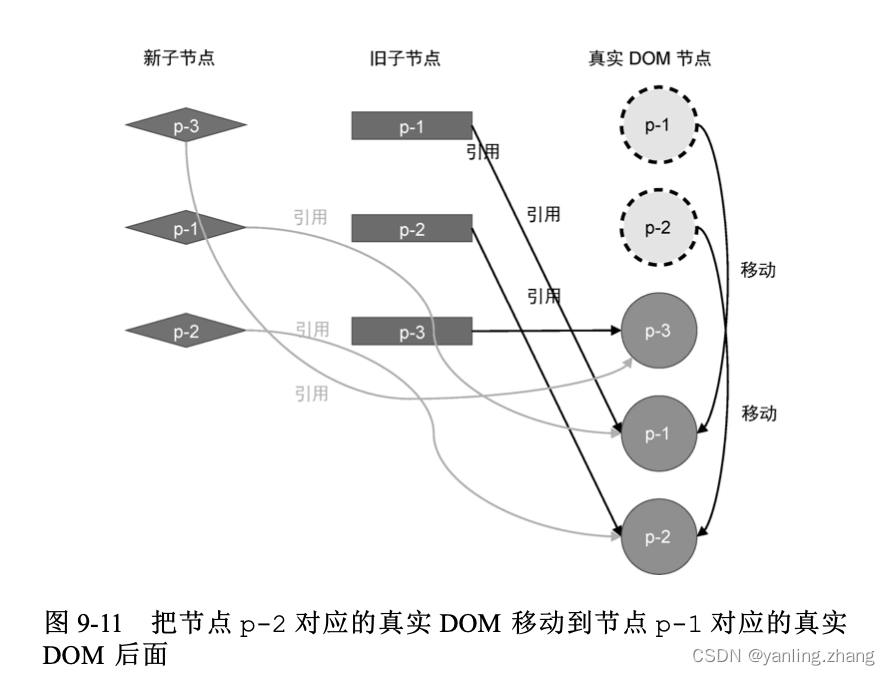
经过这一步移动操作之后,我们发现,真实 DOM 的顺序与新的一组子节点的顺序相同了:p-3、p-1、p-2。至此,更新操作完成。
function patchChildren(n1, n2) {const oldChildren = n1.childrenconst newChildren = n2.childrenlet lastIndex = 0for (let i = 0; i < newChildren.length; i++) {const newVNode = newChildren[i]for (j = 0; j < oldChildren.length; j++) {const oldVNode = oldChildren[j]if (newVNode.key === oldVNode.key) {// 移动DOM之前,我们需要先完成打补丁操作patch(oldVNode, newVNode, container)if (j < lastIndex) {// console.log('需要移动的节点', newVNode, oldVNode, j)// 如何移动元素const prevVNode = newChildren[i - 1]if (prevVNode) {// 2.找到 prevVNode 所对应真实 DOM 的下一个兄 弟节点,并将其作为锚点const anchor = prevVNode?.el?.nextSiblingconsole.log('插入', prevVNode, anchor)}} else {lastIndex = j}break;}}}
}
patchChildren(oldVNode, newVNode)
在上面这段代码中,如果条件j < lastIndex成立,则说明当 前 newVNode 所对应的真实 DOM 需要移动。根据前文的分析可知, 我们需要获取当前 newVNode 节点的前一个虚拟节点,即 newChildren[i - 1],然后使用insert函数完成节点的移动, 其中 insert 函数依赖浏览器原生的 insertBefore 函数。
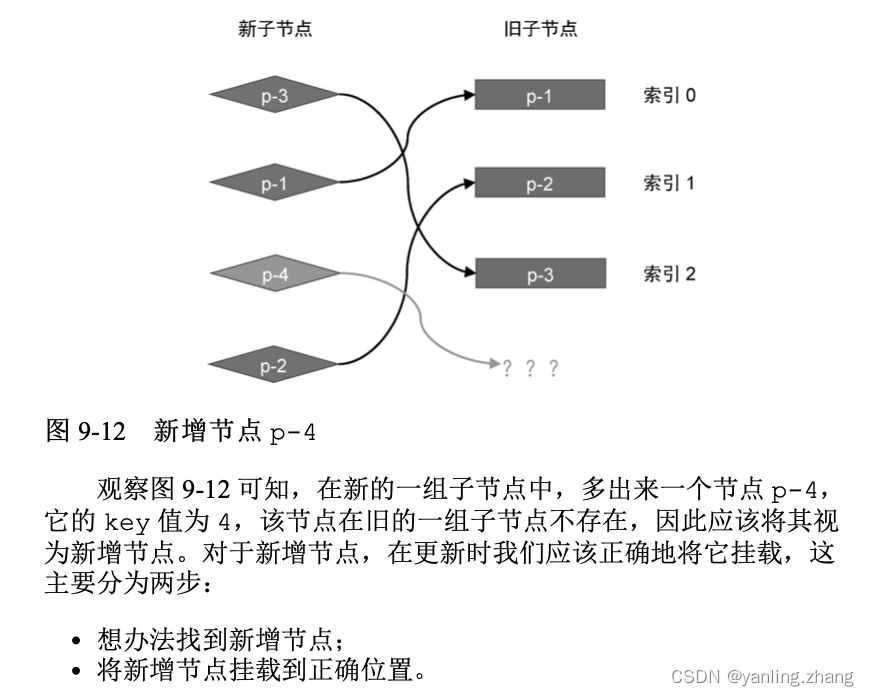
添加新元素
function patchChildren(n1, n2) {const oldChildren = n1.childrenconst newChildren = n2.childrenlet lastIndex = 0for (let i = 0; i < newChildren.length; i++) {// 在第一层循环中定义变量 find,代表是否在旧的一组子节点中找到可复用的节点let find = falseconst newVNode = newChildren[i]for (j = 0; j < oldChildren.length; j++) {const oldVNode = oldChildren[j]if (newVNode.key === oldVNode.key) {// 一旦找到可复用的节点,则将变量 find 的值设为 truefind = trueif (j < lastIndex) {// console.log('需要移动的节点', newVNode, oldVNode, j)const prevVNode = newChildren[i - 1]if (prevVNode) {// 2.找到 prevVNode 所对应真实 DOM 的下一个兄 弟节点,并将其作为锚点const anchor = prevVNode?.el?.nextSiblingconsole.log('插入', prevVNode, anchor)}} else {lastIndex = j}break;}}// 添加元素// 如果代码运行到这里,find 仍然为 false,说明当前newVNode没有在旧的一组子节点中找到可复用的节点,也就是说,当前newVNode是新增节点,需要挂载if (!find) {// 为了将节点挂载到正确位置,我们需要先获取锚点元素// 首先获取当前 newVNode 的前一个 vnode 节点const prevVNode = newChildren[i - 1] let anchor = nullif (prevVNode) {// 如果有前一个 vnode 节点,则使用它的下一个兄弟节点作为锚点元 anchor = prevVNode.el.nextSibling} else {// 如果没有前一个 vnode 节点,说明即将挂载的新节点是第一个子节// // 这时我们使用容器元素的 firstChild 作为锚点anchor = container.firstChild}// 挂载 newVNodepatch(null, newVNode, container, anchor)}}
}
patchChildren(oldVNode, newVNode)
移除不存在的元素
// 4.移除不存在的元素
function patchChildren(n1, n2) {const oldChildren = n1.childrenconst newChildren = n2.childrenlet lastIndex = 0for (let i = 0; i < newChildren.length; i++) {// 在第一层循环中定义变量 find,代表是否在旧的一组子节点中找到可复用的节点let find = falseconst newVNode = newChildren[i]for (j = 0; j < oldChildren.length; j++) {const oldVNode = oldChildren[j]if (newVNode.key === oldVNode.key) {// 一旦找到可复用的节点,则将变量 find 的值设为 truefind = trueif (j < lastIndex) {// console.log('需要移动的节点', newVNode, oldVNode, j)const prevVNode = newChildren[i - 1]if (prevVNode) {// 2.找到 prevVNode 所对应真实 DOM 的下一个兄 弟节点,并将其作为锚点const anchor = prevVNode?.el?.nextSiblingconsole.log('插入', prevVNode, anchor)}} else {lastIndex = j}break;}}// 如果代码运行到这里,find 仍然为 false,说明当前newVNode没有在旧的一组子节点中找到可复用的节点,也就是说,当前newVNode是新增节点,需要挂载if (!find) {const prevVNode = newChildren[i - 1] }}// 移除不存在的元素for (let i = 0; i < oldChildren.length; i++) {const oldVNode = oldChildren[i]const has = newChildren.find(vnode => vnode.key === oldVNode.key)// 如果没有找到具有相同 key 值的节点,则说明需要删除该节点if (!has) {// 调用 unmount 函数将其卸载unmount(oldVNode)}}
}
patchChildren(oldVNode, newVNode)
相关文章:

vuejs 设计与实现 - 简单diff算法
DOM 复用与key的作用: DOM 复用什么时候可复用? key 属性就像虚拟节点的“身份证”号,只要两个虚拟节点的 type属性值和 key 属性值都相同,那么我们就认为它们是相同的,即可以进行 DOM 的复用。即 我们通过【移动】来…...
【前端|Javascript第3篇】探秘JavaScript的作用域与作用域链:小白也能轻松搞懂!
大家好!欢迎来到本篇博客,今天我们将解开JavaScript编程世界中的一道神秘面纱:作用域与作用域链。很多Javascript开发者并不真正理解它们,但这些概念对掌握Javascript至关重要。如果你对这些概念感到困惑,不要担心&…...

【Spring AOP】结合日志面向切面编程 两种写法
概念 这里需要提前了解什么是Spring的AOP(Aspect Oriented Programming)。是在OOP(面向对象)思想的一种拓展思想。简单来说就是将某个代码块嵌入到其它的代码块中。笔者先前学Spring也有学什么IoC啊AOP啊,但实际上没有…...
C#在自动化领域的应用前景与潜力
人机界面(HMI)开发:使用C#开发人机界面软件,实现与自动化设备的交互和监控。C#的图形界面设计能力和丰富的控件库使得开发人员能够创建直观、易用的界面。 数据采集与处理:C#可以与各种传感器、设备进行数据通信和采集…...

string模拟实现:
string模拟实现: 上一篇博客,我们对String类有了一个基本的认识,本篇博客我们来从0~1去模拟实现一个String类,当然我们实现的都是一些常用的接口。 ❓我们这里定义了一个string类型,然后STL标准库里面也有string&#…...
)
系统与软件安全研究(八)
FUZZ101入门 Detail gcc,clang,llvm都有啥区别GCC (GNU Compiler Collection), Clang, 和 LLVM 都是用于编译代码的工具链。它们在某些方面有相似之处,但也有一些重要的区别。 GCC (GNU Compiler Collection):GCC 是由 GNU 组织开发的,是一个非常流行的开源编译器集合。它…...
jmeter测试rpc接口-使用dubbo框架调用【杭州多测师_王sir】
1.基于SOAP架构。基于XML规范。基于WebService协议。特点:接口地址?wsdl结尾2.基于RPC架构,基于dubbo协议,thrift协议。SpringCloud微服务。3.基于RestFul架构,基于json规范。基于http协议(我们常用的都是这种,cms平台也是) Rest…...

Java8中forEach()里使用return的效果
先总结:使用forEach()处理集合时不能使用break和continue这两个方法,可以使用无返回值的return跳出此次循环,效果同标准for循环的continue。 首先,forEach()先对入参判空,然后使用增强for循环调用action.accept(t)&am…...

MVC配置原理
如果你想保存springboot的mvc配置并且还想自己添加自己的配置就用这个。 视图解析器原理,它会从IOC容器里获取配置好视图解析器的配置类里的视图解析器集合, 然后遍历集合,生成一个一个的视图对象,放入候选 视图里,…...

rabbitmq安装
安装erlang方案二 vi /etc/yum.repos.d/rabbitmq-erlang.repo 文件内容: In /etc/yum.repos.d/rabbitmq-erlang.repo [rabbitmq-erlang] namerabbitmq-erlang baseurlhttps://dl.bintray.com/rabbitmq-erlang/rpm/erlang/22/el/7 gpgcheck1 gpgkeyhttps://dl.bi…...

轻松抓取网页内容!API助力开发者,快速数据采集
在如今这个信息爆炸的时代,人们需要从各种渠道获取数据来支持自己的业务需求。而对于开发者们来说,如何快速、准确地从互联网上抓取所需的数据也成为了一项重要的技能。而抓取网页内容 API 则是一种能够帮助开发者轻松实现数据抓取的工具。 一、什么是抓…...
CSDN 直播:腾讯云大数据 ES 结合 AI 大模型与向量检索的新一代云端检索分析引擎 8月-8号 19:00-20:30
本次沙龙围绕腾讯云大数据ES产品展开,重点介绍了腾讯云ES自研的存算分离技术,以及能与AI大模型和文本搜索深度结合的高性能向量检索能力。同时,本次沙龙还将为我们全方位介绍腾讯云ES重磅推出的Elasticsearch Serverless服务,期待…...

区块链智能合约代码示例
以下是一个简单的区块链智能合约代码示例: pragma solidity ^0.4.17;contract SimpleContract {uint public myData;function setMyData(uint newData) public {myData newData;} }该合约具有以下功能: 定义了一个名为 SimpleContract 的合约。定义了一…...
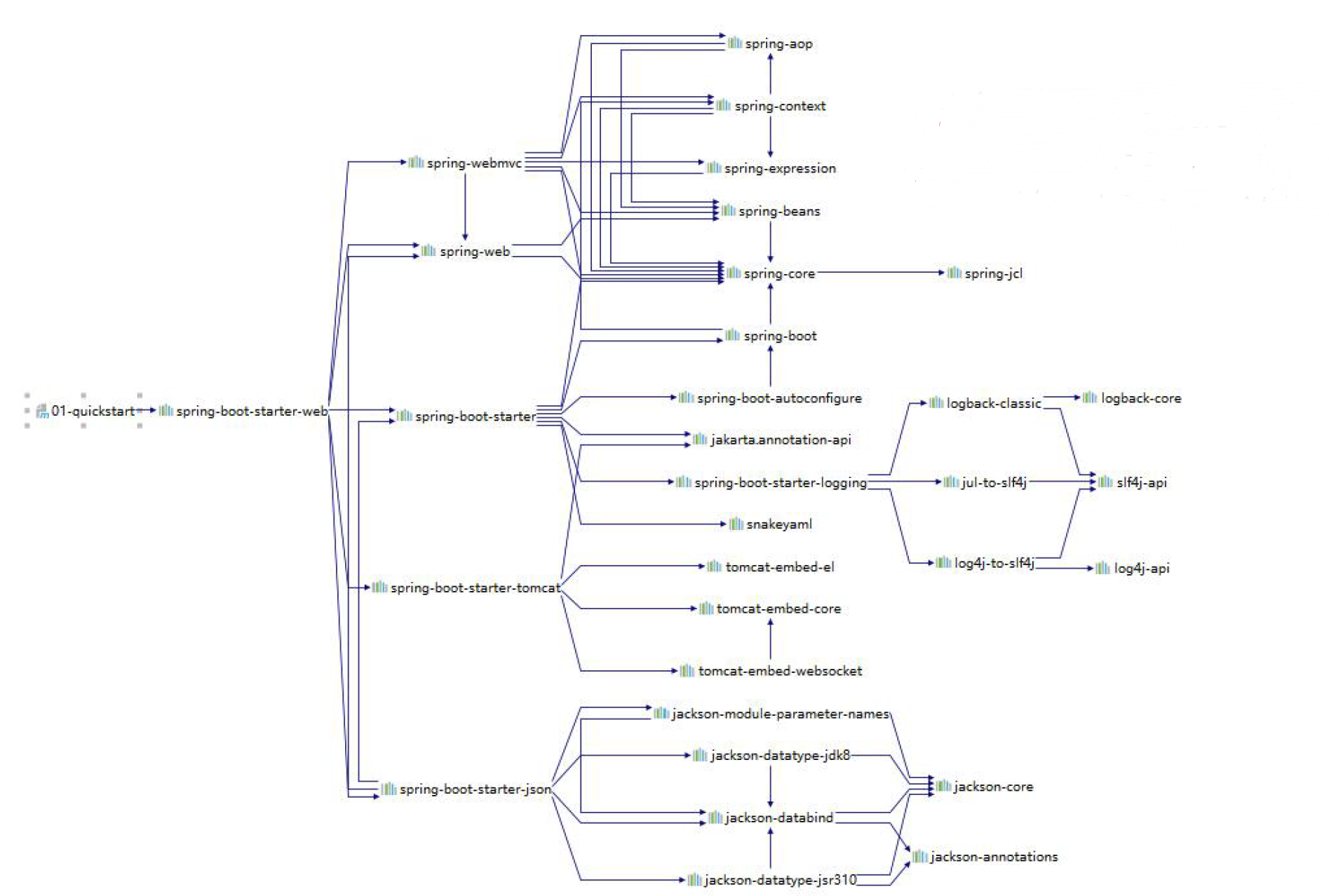
Spring Boot介绍--快速入门--约定优于配置
文章目录 SpringBoot 基本介绍官方文档Spring Boot 是什么?SpringBoot 快速入门需求/图解说明完成步骤快速入门小结 Spring SpringMVC SpringBoot 的关系总结梳理关系如何理解-约定优于配置 SpringBoot 基本介绍 官方文档 官网: https://spring.io/projects/spring-boot 学习…...
Scons编译lib库
实例目录结构: include文件夹:test.hsrc文件夹:test.cSConscriptSConstruct 如下图所示: SConstruct: #执行当前目录下的SConscript SConscript(SConscript);SConscript: import os from SCons.Script…...

React源码解析18(1)------ React.createElement 和 jsx
1.React.createElement 我们知道在React17版本之前,我们在项目中是一定需要引入react的。 import React from “react” 即便我们有时候没有使用到React,也需要引入。原因是什么呢? 在React项目中,如果我们使用了模板语法JSX&am…...

系列3-常见的高可用MySQL解决方案
高可用主要解决两个问题,如何实现数据共享和同步数据、如何处理failover,数据共享的解决方案一般是SAN,数据同步通过rsync和drbd技术来实现。 1、主从复制解决方案 这是MySQL自身的高可用解决方案,数据同步方法采用的是MySQL rep…...

C#登录后携带cookie爬取数据
前一段时间,公司以前的一个数据采集任务突然之间采集下来的数据都是0了,也就是未登录状态能够获取到的数据,于是猜想肯定是网站的服务升级了,升级了数据接口的逻辑,于是便开始解决此问题。 此采集程序是由.net core开…...

自动驾驶国家新一代人工智能开放创新平台产业化应用
【摘要】:当前,全球新一轮科技革命和产业变革正孕育兴起,自动驾驶作为人工智能最重要的应用载体之一,对于加快交通强国、智能汽车强国建设,具有十分突出的战略意义。我国自动驾驶研发应用,面临技术、资金、应用等诸多挑战,为此,需要打造一套符合我国国情的自动驾驶系统…...
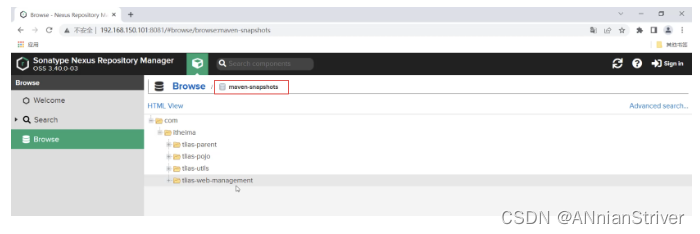
Maven分模块-继承-聚合-私服的高级用法
Maven分模块-继承-聚合-私服的高级用法 JavaWeb知识,介绍Maven的高级用法!!! 文章目录 Maven分模块-继承-聚合-私服的高级用法1. 分模块设计与开发1.1 介绍1.2 实践1.2.1 分析1.2.2 实现 1.3 总结 2. 继承与聚合2.1 继承2.1.1 继承…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...
