从前序与中序遍历序列构造二叉树,从中序与后序遍历序列构造二叉树
目录
- 从前序与中序遍历序列构造二叉树
- 从中序与后序遍历序列构造二叉树
从前序与中序遍历序列构造二叉树
题目链接
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
实例1:
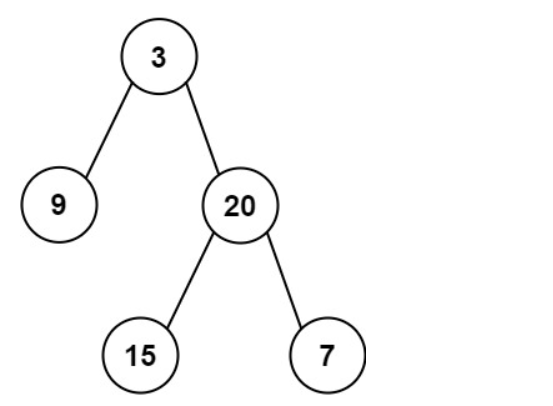
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
首先我们应该明白,
前序遍历就是,先遍历根节点,然后遍历左子树,最后遍历右子树
中序遍历就是,先遍历左子树,然后遍历根节点,最后遍历右子树
后续遍历就是,先遍历左子树,然后遍历右子树,最后遍历根节点
首先我们先试着用前序与中序遍历序列构造一棵二叉树
给出前序遍历数列 preorder 和 中序遍历数列 inorder
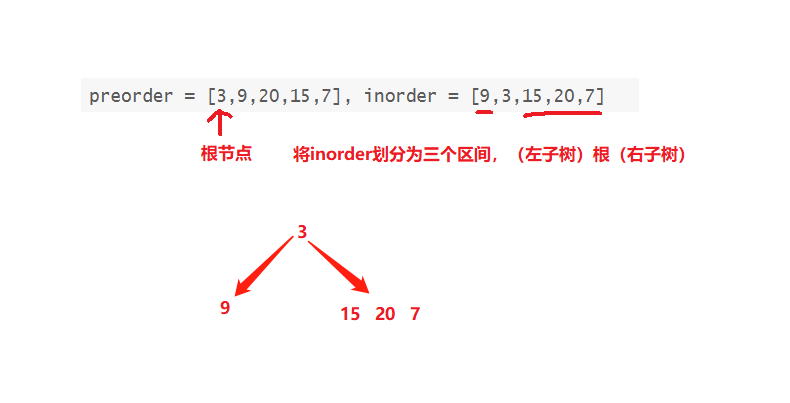
我们知道前序遍历二叉树必然先走根节点,所以我们可知preorder序列中的第一个数字3即为二叉树的根节点,中序遍历数列中,左子树必然先于右子树遍历,所以我们可知,在中序遍历数列inorder中的使用根节点将inorder划分为三个区间,(左子树)根(右子树),根节点3左边的元素为左子树,3右边的元素为右子树
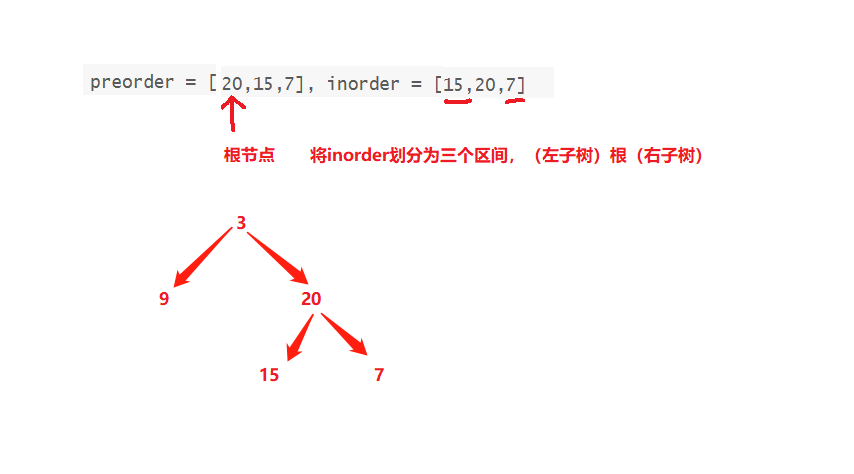
现在3的左子树为空,右子树(15,20,7)继续使用相同方法构造二叉树
代码:
采用递归调用,分解子问题的方法
class Solution {
public:TreeNode* build(vector<int>& preorder,vector<int>& inorder,int& prev,int inbegin,int inend){ //perorder 前序遍历序列,inorder 中序遍历序列,prev 指向前序遍历数列下标if(inbegin>inend)return NULL;//当前的根节点TreeNode* root=new TreeNode(preorder[prev]);int rooti=inbegin; //用来查找根节点在数组中的下班位置while(rooti<inend){if(inorder[rooti]==preorder[prev])break;rooti++;}prev++; //每次使用完prev需往后走,prev指的是数组前序遍历中用来判断根节点的//划分区间,(左子树,根)根(根,右子树)// (inbegin,rooti-1)rooti(rooti+1,inend)//函数递归继续构造二叉树的左右节点root->left=build(preorder,inorder,prev,inbegin,rooti-1); root->right=build(preorder,inorder,prev,rooti+1,inend);return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int i=0;TreeNode* root=build(preorder,inorder,i,0,inorder.size()-1);return root;}
};
从中序与后序遍历序列构造二叉树
题目链接
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
实例1:
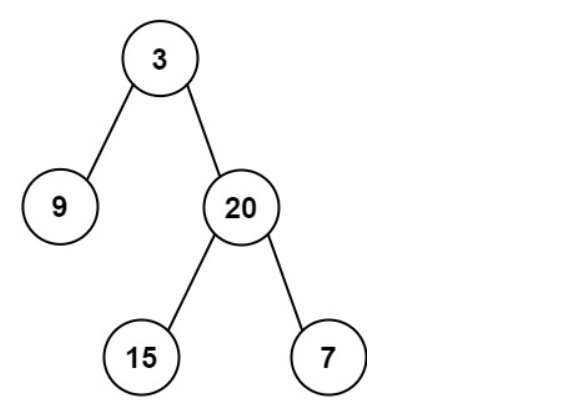
输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出:[3,9,20,null,null,15,7]
使用中序与后序遍历序列构造二叉树 思路根前序与中序序列构造二叉树相似
给出二叉树的中序遍历inorder 和 后续遍历 postorder
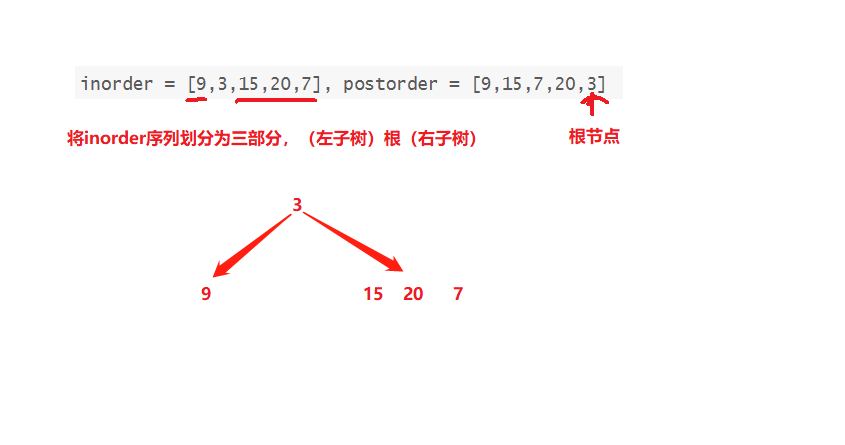
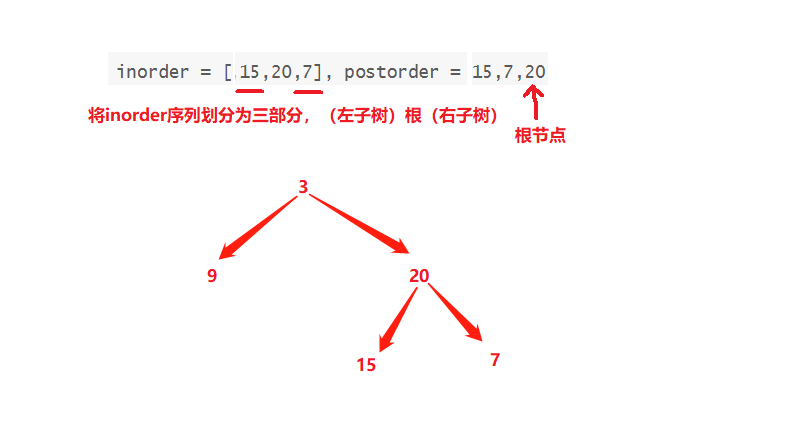
我们知道后续遍历二叉树,根节点最后遍历,所以我们可知postorder序列中的最后一个元素3即为二叉树的根节点,中序遍历数列中,左子树优于根先遍历,右子树后于根遍历,所以我们可以根据这两个条件将inorder序列划分为三个区间,(左子树)根(右子树),根节点3左边的元素为左子树,3右边的元素为右子树
3的左子树序列只剩一个,即为3的左节点,右子树序列还有三个元素,需要继续划分,重复上述过程
代码:
class Solution {
public:TreeNode* build(vector<int>& inorder, vector<int>& postorder,int& prev,int inbegin,int inend){if(inbegin>inend)return NULL;TreeNode* root=new TreeNode(postorder[prev]);int rooti=inbegin;while(rooti<inend){if(postorder[prev]==inorder[rooti])break;rooti++;}prev--;// (左,根)根(根,右)//先构造右子树,再构造左子树root->right=build(inorder,postorder,prev,rooti+1,inend);root->left=build(inorder,postorder,prev,inbegin,rooti-1);return root;}TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {int i=postorder.size()-1;TreeNode* root=build(inorder,postorder,i,0,postorder.size()-1);return root;}
};
相关文章:
从前序与中序遍历序列构造二叉树,从中序与后序遍历序列构造二叉树
目录 从前序与中序遍历序列构造二叉树从中序与后序遍历序列构造二叉树 从前序与中序遍历序列构造二叉树 题目链接 给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返…...

【JS常见数据结构】
JS数据结构 前言数组JavaScript 中数组的常见操作:1. 创建数组:2. 访问数组元素:3. 插入元素:4. 删除元素:5. 查询元素: 链表单向链表双向链表循环链表 栈队列树二叉树示例 图图的定义图的分类图的表示方法…...

算法基础之插入排序
1、插入排序基本思想 插入排序的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序)&a…...

InfoQ 分享
...
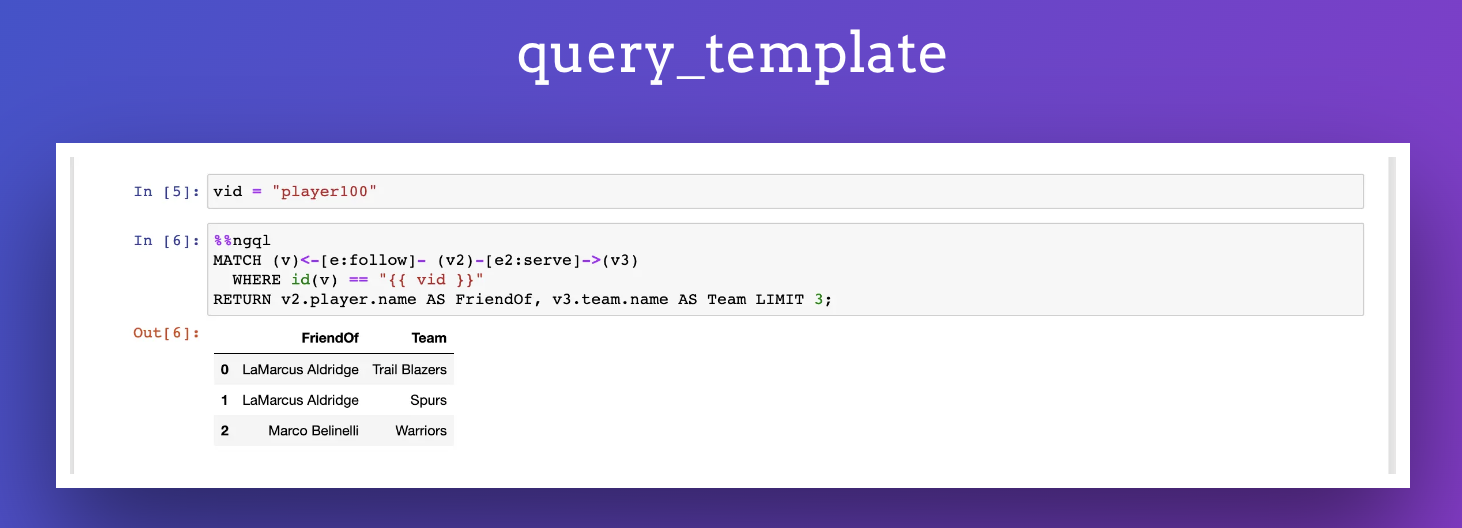
Jupyter Notebook 遇上 NebulaGraph,可视化探索图数据库
在之前的《手把手教你用 NebulaGraph AI 全家桶跑图算法》中,除了介绍了 ngai 这个小工具之外,还提到了一件事有了 Jupyter Notebook 插件: https://github.com/wey-gu/ipython-ngql,可以更便捷地操作 NebulaGraph。 本文就手把手教你咋在 J…...

人类与机器的分类不同
分类能力也是智能的重要标识之一。通过分类,我们可以将事物或概念进行归类和组织,从而更好地理解和处理信息。分类在人类认知和智能发展中起到了重要的作用,它有助于我们对世界进行认知、记忆、推理和决策。在机器智能领域,分类同…...

WEB安全-SQL注入,CSRF跨站伪造,OXX跨站脚本
SQL 注入攻击 SQL 注入是一种网络攻击手段,攻击者通过在 Web 应用程序的输入字段中插入恶意 SQL 代码,试图访问、篡改或删除数据库中的数据。这种攻击通常发生在应用程序未对用户输入进行充分验证或过滤的情况下。 举个例子,例如,…...

【HDFS】客户端读某个块时,如何对块的各个副本进行网络距离排序?
本文包含如下内容: ① 通过图解+源码分析/A1/B1/node1和 /A1/B2/node2 这两个节点的网络距离怎么算出来的 ② 客户端读文件时,副本的优先级。(怎么排序的,排序规则都有哪些?) ③ 我们集群发现的一个问题。 客户端读时,通过调用getBlockLocations RPC 获取文件的各个块。…...

【数字化处理】仿生假体控制中肌电信号的数字化处理研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

谷歌推出Flax:JAX的神经网络库
在优化理论中,损失或成本函数测量拟合或预测值与实际值之间的距离。对于大多数机器学习模型,提高性能意味着最小化损失函数。 但对于深度神经网络,执行梯度下降以最小化每个参数的损失函数可能会消耗大量资源。传统方法包括手动推导和编码&a…...

PDF换行的难度,谁能解决?
换行的时候确认不了长度: import java.awt.*;public class Test {public static void main(String[] args) {String str1 "淘淘淘淘淘淘淘淘淘淘淘淘淘淘淘淘淘淘淘淘淘淘淘淘淘淘淘淘淘淘淘淘淘淘淘淘淘";String str2 "AAAAAAAAAAAAAAAAAAAAAAAAA…...

山东布谷科技直播程序源码使用Redis进行服务器横向扩展
当今,直播程序源码平台作为新媒体时代主流,受到了世界各地人民的喜爱,这也使得直播程序源码平台用户数量的庞大,也难免会出现大量用户同时访问服务器,使服务器过载的情况,当服务器承受不住的时候࿰…...

symfony3.4中根据角色不同跳转不同页面
在Symfony 3.4中,可以使用安全组件来实现控制不同角色跳转到不同页面的功能。 首先,确保你已经安装了Symfony的安全组件,并配置了安全相关的配置文件。这些文件通常是 security.yml 和 security.yml。 在配置文件中,你可以定义不…...
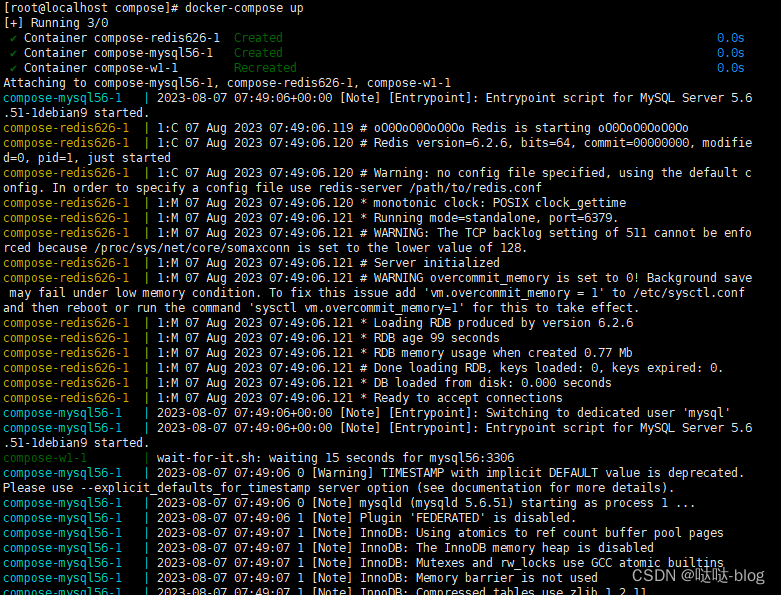
Dockerfile部署golang,docker-compose
使用go镜像打包,运行在容器内 redis和mysql用外部的 项目目录结构 w1go项目: Dockerfile # 这种方式是docker项目加上 本地的mysql和redis环境 # go打包的容器 FROM golang:alpine AS builder# 为我们镜像设置一些必要的环境变量 ENV GO111MODULEon …...
什么是Linux,如何在Windows操作系统下搭建Linux环境,远程连接Linux系统
文章目录 什么是LinuxLinux的诞生及发展为什么要学习LinuxLinux内核Linux发行版什么是虚拟机如何在VMware虚拟机中搭建Linux系统环境远程连接 Linux 系统Linux 帮助网站 什么是Linux Linux是一套免费使用和自由传播的类Unix操作系统,是一个基于POSIX和UNIX的多用户…...

Ubuntu下RabbitMQ安装与简单使用
一:RabbitMQ基本安装 1.更新依赖包(提前更新依赖包避免出现报错) sudo apt-get update 2.由于rabbitMq使用erlang语言开发,在安装rabbitMq之前需要安装erlang sudo apt-get install erlang 3.查看erlang是否安装成功 sudo erl 安装成功会出现下面的提示…...

力扣62.不同路径(动态规划)
/*** 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。* 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。* 问总共有多少条不同的路径? *…...

TypeScript 泛型的概念和基本使用
什么是TypeScript 泛型? 在定义函数,接口,类的时候不能预先确定使用的数据类型,而是在调用使用这些函数,接口,类的时候才能确定的数据类型; 1,单个泛型的参数 例如通过使用any这种…...
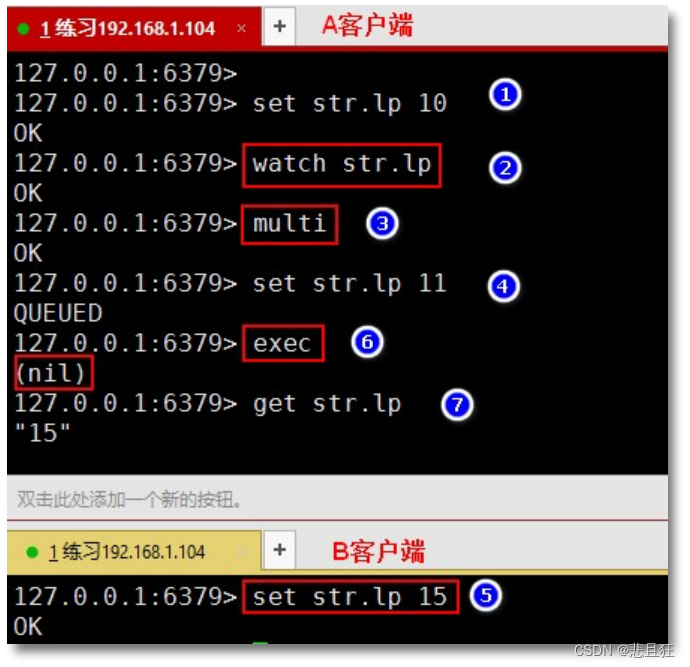
redis的事务和watch机制
这里写目录标题 第一章、redis事务和watch机制1.1)redis事务,事务的三大命令语法:开启事务 multi语法:执行事务 exec语法:取消事务 discard 1.2)redis事务的错误和回滚的情况1.3)watch机制语法&…...

objectMapper.getTypeFactory().constructParametricType 方法的作用和使用
在使用 Jackson 库进行 JSON 数据的序列化和反序列化时,经常会使用到 ObjectMapper 类。其中,objectMapper.getTypeFactory().constructParametricType 方法用于构造泛型类型。 具体作用和使用如下: 作用: 构造泛型类型&#x…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

二叉树-144.二叉树的前序遍历-力扣(LeetCode)
一、题目解析 对于递归方法的前序遍历十分简单,但对于一位合格的程序猿而言,需要掌握将递归转化为非递归的能力,毕竟递归调用的时候会调用大量的栈帧,存在栈溢出风险。 二、算法原理 递归调用本质是系统建立栈帧,而非…...