算法通关村第六关——如何使用中序和后序来恢复一颗二叉树
1 树的基础知识
1.1 树的定义
树(Tree):表现得是一种层次关系,为 n ( n ≥ 0 ) n(n≥0) n(n≥0)个节点构成的有限集合,当n=0时,称为空树,对于任一颗非空树(n>0),它具备以下性质:
-
树中有一个根(root)节点,用
r表示 -
其余节点可分为
m(m>0)个互不相交的有限集 T 1 , T 2 , . . . , T m \bold{T_1,T_2, ...,T_m} T1,T2,...,Tm ,其中每个集合本身又是一棵树,称为原来树的子树(Subtree)。子树不相交;除了根结点外,每个结点有且仅有一个父结点;一颗N个结点的树有N-1条边。
树的一些基本术语:
- 结点的度(Degree):结点的子树个数
- 树的度:树的所有结点中最大的度数
- 叶结点(Leaf):度为0的结点
- 父结点(Parent):有子树的结点是其子树的根节点的父结点
- 子结点(Child):若A结点是B结点的父结点,则称B结点是A结点的子结点;子结点也称孩子结点。
- 兄弟结点(Sibling):具有同一父结点的各结点是彼此的兄弟结点。
- 路径和路径长度:从结点 n 1 n_1 n1到 n x n_x nx的路径为一个结点序列 n , n 2 , . . . , n x n,n_2 ,... , n_x n,n2,...,nx , n i n_i ni 是 n i + 1 n_{i+1} ni+1 的父结点。路径所包含边的个数为路径的长度。
- 祖先结点(Ancestor):沿树根到某一结点路径上的所有结点都是这个结点的祖先结点。
- 子孙结点(Descendant):某一结点的子树中的所有结点是这个结点的子孙。
- 结点的层次(Level):规定根结点在1层,其它任一结点的层数是其父结点的层数加1。
- 树的深度( Depth):树中所有结点中的最大层次是这棵树的深度。
- 森林:由
m(m > 0)棵互不相交的树的集合称为森林。- 无序树:树中任意节点的子节点之间没有顺序关系,这种树称为无序树也称为自由树。
- 有序树:树中任意节点之间有顺序关系,这种树称为有序树;
- 二叉树:每个结点最多含有两个子树的树称为二叉树
1.2 树的性质
-
一个二叉树第
i层的最大结点数为: 2 i − 1 , i ≥ 1 2^{i-1},i≥1 2i−1,i≥1 -
深度为
k的二叉树有最大结点总数为: 2 k − 1 , k ≥ 1 2^k-1,k≥1 2k−1,k≥1 -
对任何非空二叉树 T T T ,若 n 0 n_0 n0 表示叶结点的个数, n 2 n_2 n2 是度为2的非叶结点个数,那么两者满足关系 n 0 = n 2 + 1 n_0=n_2+1 n0=n2+1
-
具有n个结点的完全二叉树的深度必为 l o g 2 ( n + 1 ) log_2(n+1) log2(n+1)
-
对完全二叉树,若从上至下、从左至右编号,则编号为
i的结点,其左孩子编号必为2i,其右孩子编号必为2i+1;其双亲的编号必为 i 2 \frac{i}{2} 2i(i=1时为根,除外)对二叉树的重要操作:主要是遍历。
满二叉树:如果一棵二叉树只有度为0的节点和度为2的节点,并且度为0的节点在同一层上,则这棵二叉树为满二叉树。

完全二叉树:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大 值,并且最下面一层的节点都集中在该层最左边的若干位置。

1.3 树的存储方式
-
顺序存储结构
- 完全二叉树:按从上至下、从左到右顺序结构

- 链表存储

1.4 树的遍历方式
- 深度优先遍历:先往深走,遇到叶子节点再往回走。
- 前序遍历(中左右)
- 中序遍历(左中右)
- 后序遍历(左右中)

- 广度优先遍历(层次遍历):一层一层的去遍历,一层访问完再访问下一层。
2 通过序列构造二叉树
2.1 根据后中序列复原二叉树
给定三个序列:
(1) 前序:1 2 3 4 5 6 8 7 9 10 11 12 13 15 14
(2) 中序:3 4 8 6 7 5 2 1 10 9 11 15 13 14 12
(3) 后序:8 7 6 5 4 3 2 10 15 14 13 12 11 9 1
分析:
根据后序和中序遍历来复原二叉树的思路就是先根据后序遍历确定根节点,然后中序遍历中根节点左边的是左子树,根节点右边的是右子树。根据中序遍历划分好的左右子树,在后序遍历里划分好左右子树。我们知道后序遍历最后遍历中间结点,那么就可以在后序遍历里划分好的左右子树中确定左右子树的根节点,再返回中序遍历划分左右子树。以此类推,直到复原二叉树。
第一轮:
中: 3 4 8 6 7 5 2 | 10 9 11 15 13 14 12后: 8 7 6 5 4 3 2 | 10 15 14 13 12 11 9第二轮:
中: 3 4 8 6 7 5 | null 10 | 11 15 13 14 12后: 8 7 6 5 4 3 | null 10 | 15 14 13 12 11第三轮:
中:null | 4 8 6 7 5 null | 15 13 14 12后:null | 8 7 6 5 4 null | 15 14 13 12第四轮:
中:null | 8 6 7 5 15 13 14 | null后:null | 8 7 6 5 15 14 13 | null第五轮:
中: 8 6 7 | null 15 | 14后: 8 7 6 | null第六轮:
中: 8 | 7
复原后的二叉树:

2.2 根据前中序列复原二叉树
分析:
根据前序遍历和中序遍历来复原二叉树,与根据后序遍历和中序遍历复原二叉树不同之处在于前序遍历先遍历根结点,再遍历左右结点。先根据前序遍历找到根结点,再在中序遍历中划分左右子树,之后根据中序遍历划分的左右子树来对前序遍历的左右子树进行划分,之后再找左右子树的根结点。以此类推,直到复原。
过程不再赘述,与根据后序遍历和中序遍历复原二叉树大同小异。
相关文章:

算法通关村第六关——如何使用中序和后序来恢复一颗二叉树
1 树的基础知识 1.1 树的定义 树(Tree):表现得是一种层次关系,为 n ( n ≥ 0 ) n(n≥0) n(n≥0)个节点构成的有限集合,当n0时,称为空树,对于任一…...

leetcode算法题--判断是否能拆分数组
原题链接:https://leetcode.cn/problems/check-if-it-is-possible-to-split-array/ 一开始思路想错了。。导致浪费很多时间 其实只要能找到存在一个子数组,子数组长度为2,这个子数组符合条件就一定能拆分。。 func canSplitArray(nums []i…...
基于Flask的模型部署
基于Flask的模型部署 一、背景 Flask:一个使用Python编写的轻量级Web应用程序框架; 首先需要明确模型部署的两种方式:在线和离线; 在线:就是将模型部署到类似于服务器上,调用需要通过网络传输数据&…...

【资料分享】全志科技T507-H开发板规格书
1 评估板简介 创龙科技TLT507-EVM是一款基于全志科技T507-H处理器设计的4核ARM Cortex-A53国产工业评估板,主频高达1.416GHz,由核心板和评估底板组成。核心板CPU、ROM、RAM、电源、晶振等所有器件均采用国产工业级方案,国产化率100%。同时,评估底板大部分元器件亦采用国产…...
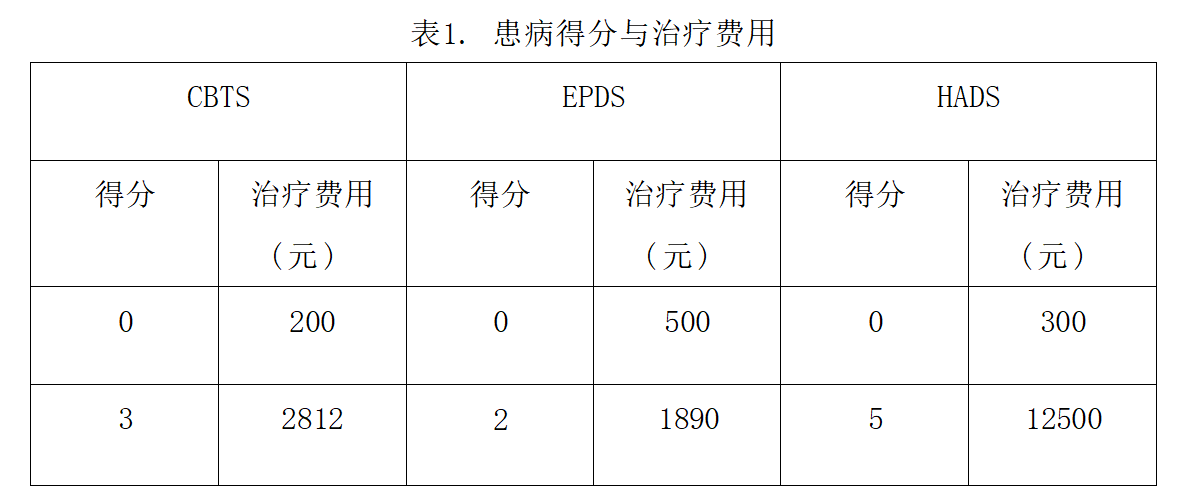
2023华数杯数学建模C题思路 - 母亲身心健康对婴儿成长的影响
# 1 赛题 C 题 母亲身心健康对婴儿成长的影响 母亲是婴儿生命中最重要的人之一,她不仅为婴儿提供营养物质和身体保护, 还为婴儿提供情感支持和安全感。母亲心理健康状态的不良状况,如抑郁、焦虑、 压力等,可能会对婴儿的认知、情…...
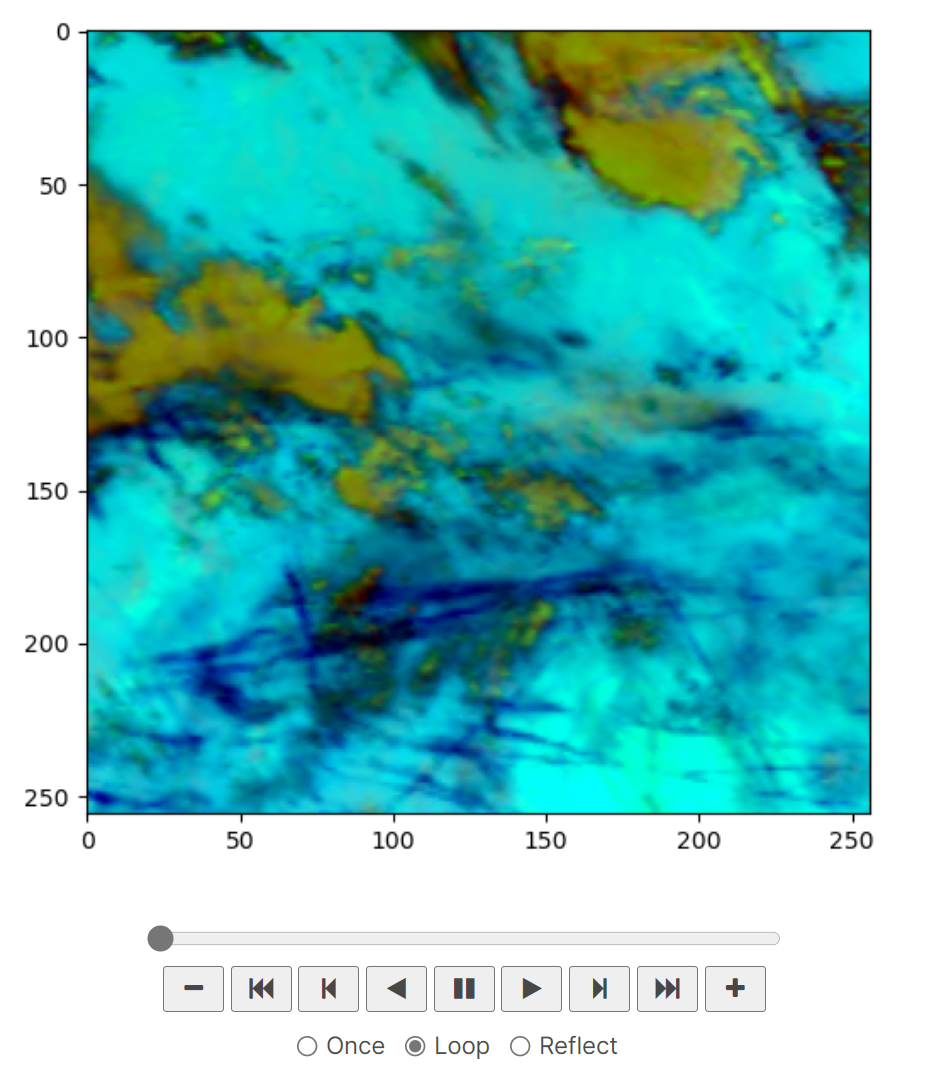
【Kaggle】Identify Contrails to Reduce Global Warming 比赛数据集的可视化(含源代码)
一、数据简单解读 卫星图像最初来自: https://www.goes-r.gov/spacesegment/abi.html高级基线成像仪是GOES-R系列中用于对地球天气、海洋和环境进行成像的主要仪器。ABI用16个不同的光谱波段观察地球(上一代GOES只有<>个),…...
 BeanFactory 和 ApplicationContext 区别)
Spring(12) BeanFactory 和 ApplicationContext 区别
目录 一、BeanFactory 和 ApplicationContext 区别?二、既然 Spring Boot 中使用的是 ApplicationContext 进行应用程序的启动和管理,那么 Spring Boot 会用到 BeanFactory 吗? 一、BeanFactory 和 ApplicationContext 区别? Bea…...
git的日常使用
加入忽略列表:在.gitignore中加入忽略的文件,build/ 表示build文件夹下,*.jar 表示以jar结尾的,用换行符隔开将另一个分支合并到当前分支:git merge xxx冲突出现,可以看看这里:详解Git合并冲突—…...

【Spring Boot】请求参数传json对象,后端采用(pojo)CRUD案例(102)
请求参数传json对象,后端采用(pojo)接收的前提条件: 1.pom.xml文件加入坐标依赖:jackson-databind 2.Spring Boot 的启动类加注解:EnableWebMvc 3.Spring Boot 的Controller接受参数采用:Reque…...
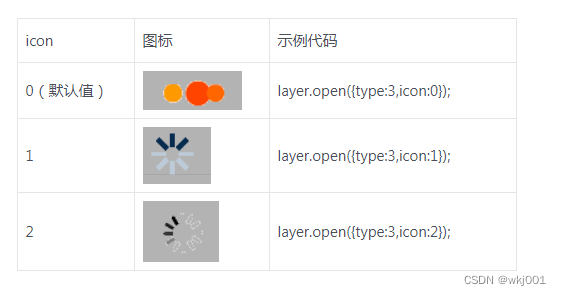
layui之layer弹出层的icon数字及效果展示
layer的icon样式 icon如果在信息提示弹出层值(type为0)可以传入0-6,icon与图标对应关系如下: 如果是加载层(type为3)可以传入0-2,icon与图标对应关系如下:...

Python selenium对应的浏览器chromedriver版本不一致
1、chrome和chromedriver版本不一致导致的,我们只需要升级下chromedriver的版本即可 浏览器版本查看 //打开google浏览器直接访问,查看浏览器版本 chrome://version/ 查看chromedriver的版本 //查看驱动版本 chromedriver chromedriver下载 可看到浏…...
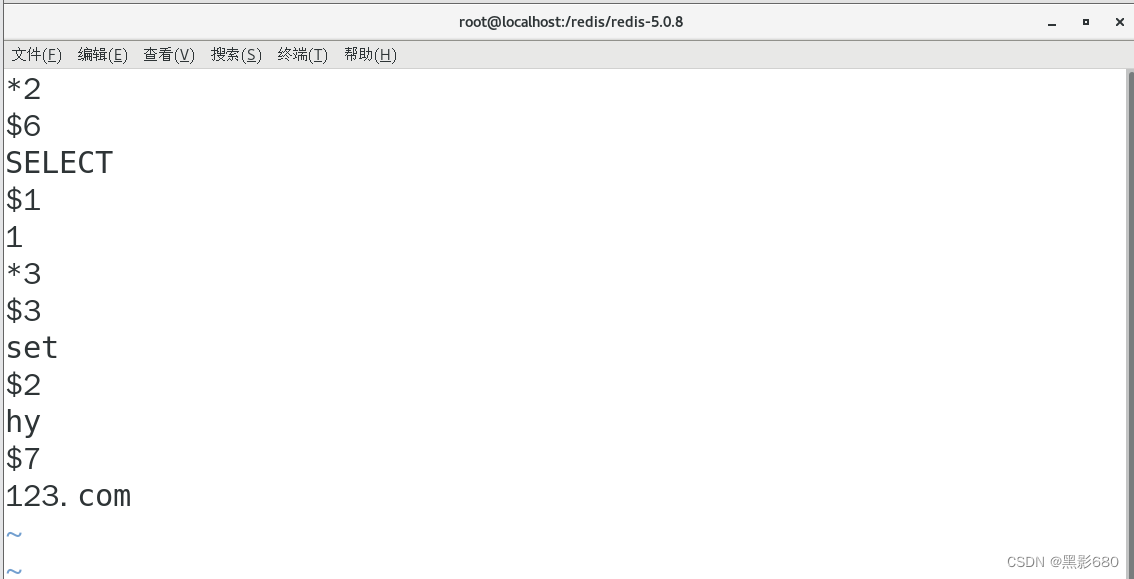
Redis的安装方法与基本操作
目录 前言 一、REDIS概述 二、REDIS安装 1、编译安装 2.yum安装 三、Redis的目录结构 四、基础命令解析 五、在一台服务器上启动多个redis 六、数据库的基本操作 (一)登录数据库 (二)基础命令 七、Redis持久化 (一&…...

选读SQL经典实例笔记20_Oracle语法示例
1. 计算一年有多少天 1.1. sql select Days in 2005: ||to_char(add_months(trunc(sysdate,y),12)-1,DDD)as reportfrom dualunion allselect Days in 2004: ||to_char(add_months(trunc(to_date(01-SEP-2004),y),12)-1,DDD)from dual REPORT ----------------- Days in 200…...

JAVA细节/小技巧
一、 Callable类可以实现返回结果的多线程。实现Callable类,然后实例化一个对象传递给FutureTask,然后把FutureTask对象传递给Thread对象,执行start即可开始多线程。FutureTask对象执行get函数可以获得Callable类中call函数的返回值…...
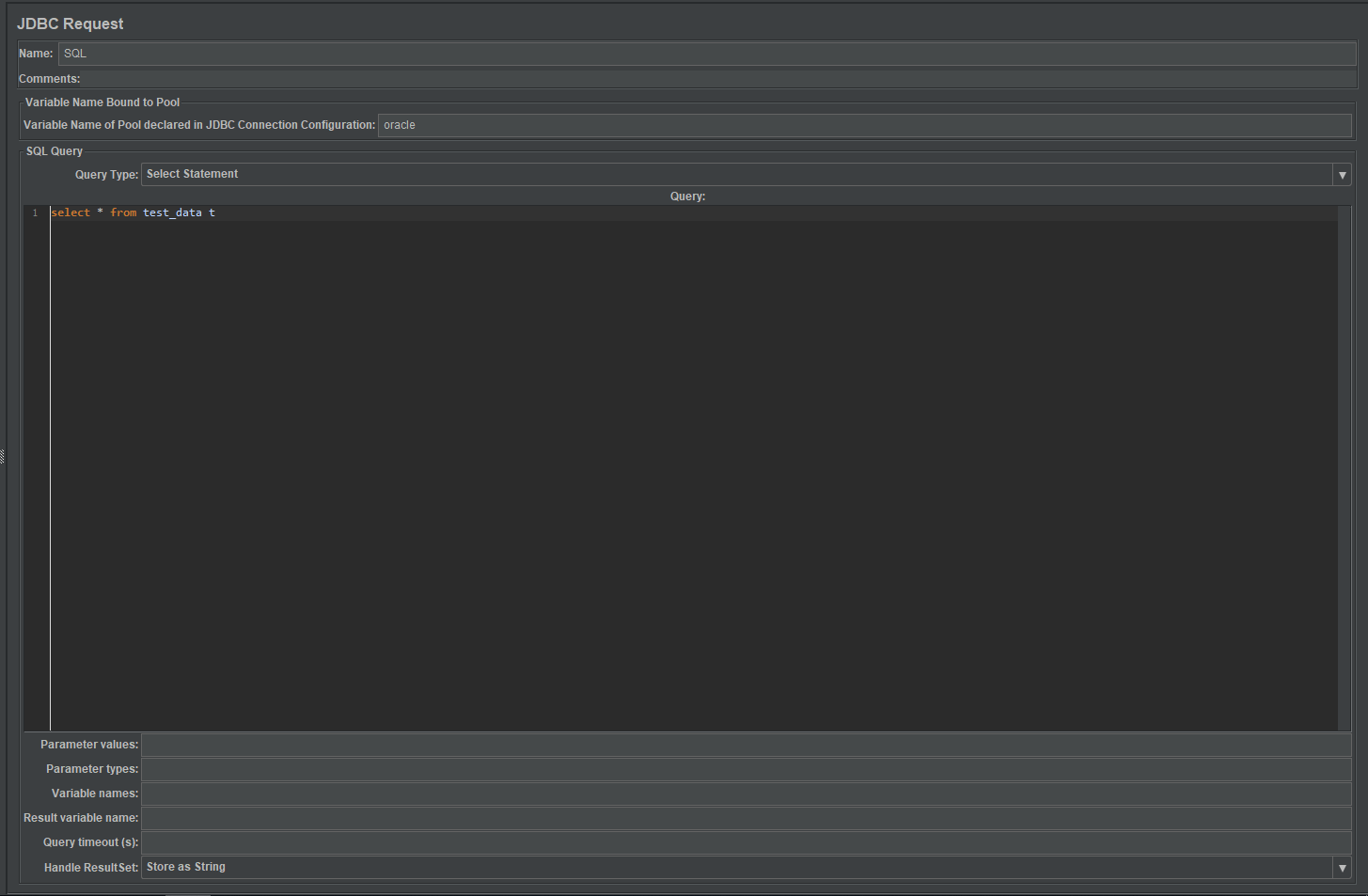
jmeter如何压测和存储
一、存储过程准备: 1、建立一个空表: 1 CREATE TABLE test_data ( id NUMBER, name VARCHAR2(50), age NUMBER ); 2、建立一个存储过程: 1 2 3 4 5 6 7 8 9 CREATE OR REPLACE PROCEDURE insert_test_data (n IN NUMBER) AS BEGIN --E…...
:Python并发编程在爬虫中的应用)
一个月学通Python(三十三):Python并发编程在爬虫中的应用
专栏介绍 结合自身经验和内部资料总结的Python教程,每天3-5章,最短1个月就能全方位的完成Python的学习并进行实战开发,学完了定能成为大佬!加油吧!卷起来! 全部文章请访问专栏:《Python全栈教程(0基础)》 再推荐一下最近热更的:《大厂测试高频面试题详解》 该专栏对…...
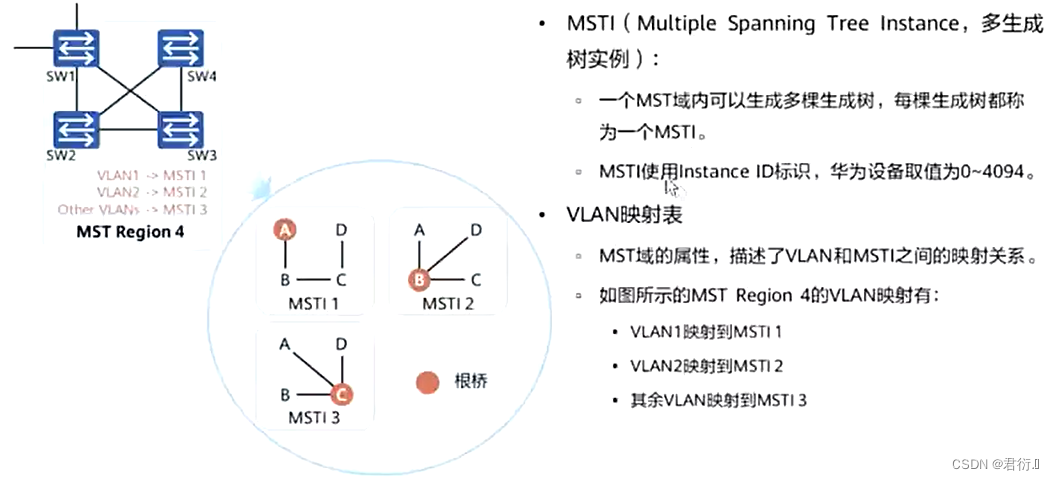
HCIP——STP
STP 一、STP概述二、二层环路带来的问题1、广播风暴问题2、MAC地址漂移问题3、多帧复制 三、802.1D生成树STP的BPDU1、配置BPDU2、RPC3、COST4、配置BPDU的工作过程5、TCN BPDU6、TCN BPDU的工作原理 四、STP的角色五、STP角色选举六、STP的接口状态七、接口状态的迁移八、STP的…...
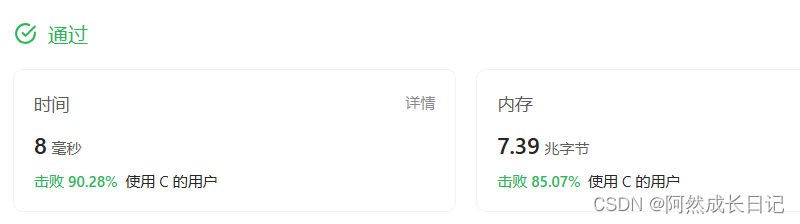
【数据结构】“单链表”的练习题
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃个人主页 :阿然成长日记 …...
项目实战 — 消息队列(5){统一硬盘操作}
前面已经使用数据库管理了交换机、绑定、队列,然后又使用了数据文件管理了消息。 那么,这里就创建一个类,讲之前的两个部分整合起来,对上层提供统一的一套接口,表示硬盘上存储的所有的类的信息。 /* * 用这个类来管理…...
【2.2】Java微服务:Hystrix的详解与使用
目录 分布式系统面临问题 Hystrix概念 Hystrix作用 降级 什么是降级 order服务导入Hystrix依赖(简单判断原则:谁调用远程谁加) 启动类添加注解 业务方法添加注解(冒号里填回调方法名,回调方法返回兜底数据&…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...
