图的遍历DFSBFS-有向图无向图
西江月・证明
即得易见平凡,仿照上例显然。留作习题答案略,读者自证不难。
反之亦然同理,推论自然成立。略去过程Q.E.D.,由上可知证毕。
有向图的遍历可以使用深度优先搜索(DFS)和广度优先搜索(BFS)两种算法来实现。
有向图的遍历
1.DFS遍历有向图的步骤:
- 选择一个起始节点,标记为已访问。
- 访问其邻接节点中第一个未被访问的节点,标记为已访问。
- 以该节点为起始节点,重复步骤2,直到没有未访问的邻接节点。
- 回溯到上一个节点,重复步骤2和步骤3,直到所有节点都被访问。
DFS遍历可以使用递归或栈来实现。
#include<bits/stdc++.h>
using namespace std;// 建立有向图
void build_graph(vector<vector<int>>& graph, int num_edges) {for (int i = 0; i < num_edges; i++) {int from, to;cin >> from >> to;graph[from].push_back(to);}
}// 有向图的深度优先遍历
void dfs(vector<vector<int>>& graph, int node, vector<bool>& visited, stack<int>& result) {visited[node] = true;for (int i = 0; i < graph[node].size(); i++) {int next_node = graph[node][i];if (!visited[next_node]) {dfs(graph, next_node, visited, result);}}result.push(node);
}// 输出拓扑排序结果
void print_topological_order(stack<int>& result) {while (!result.empty()) {cout << result.top() << " ";result.pop();}
}int main() {int num_nodes, num_edges;cin >> num_nodes >> num_edges;// 建立有向图vector<vector<int>> graph(num_nodes);build_graph(graph, num_edges);// 定义visited数组vector<bool> visited(num_nodes, false);// 定义结果栈stack<int> result;// 对每个未被遍历的节点进行深度优先遍历for (int i = 0; i < num_nodes; i++) {if (!visited[i]) {dfs(graph, i, visited, result);}}// 输出拓扑排序结果print_topological_order(result);return 0;
}2.BFS遍历有向图的步骤:
- 选择一个起始节点,标记为已访问,并将其加入队列。
- 从队列中取出第一个节点,访问其邻接节点中第一个未被访问的节点,标记为已访问,并将其加入队列。
- 重复步骤2,直到队列为空。
- 如果还有未访问的节点,选择其中一个作为新的起始节点,重复步骤1~3。
BFS遍历可以使用队列来实现。
#include<bits/stdc++.h>
using namespace std;void bfs(vector<vector<int>>& graph, vector<bool>& visited, int start) {queue<int> q;visited[start] = true;q.push(start);while (!q.empty()) {int curr = q.front();cout << curr << " ";q.pop();for (int neighbor : graph[curr]) {if (!visited[neighbor]) {visited[neighbor] = true;q.push(neighbor);}}}
}int main() {int n = 6; // number of nodes// adjacency list representation of the graphvector<vector<int>> graph(n);graph[0] = {1, 2};graph[1] = {0, 2, 3, 4};graph[2] = {0, 1, 3};graph[3] = {1, 2, 4};graph[4] = {1, 3, 5};graph[5] = {4};// mark all nodes as not visitedvector<bool> visited(n, false);// perform BFS traversal starting from node 0bfs(graph, visited, 0);return 0;
}无向图的遍历
无向图的遍历有两种方法:深度优先搜索(DFS)和广度优先搜索(BFS)。
1. 深度优先搜索(DFS)
深度优先搜索是一种递归的搜索方式,从一个起点出发,沿着一条路径一直往下搜索直到走到尽头,然后回溯到之前的节点,继续搜索其他未被访问的节点。具体步骤如下:
(1)访问起点节点,并将其标记为已访问。
(2)从起点节点出发,搜索与其直接相邻的未被访问的节点。
(3)如果找到了一个未被访问的节点,就继续以该节点为起点递归搜索,直到无法再继续搜索为止。
(4)当所有与当前节点直接相邻的节点都被访问过,回溯到之前的节点,继续搜索其他未被访问的节点。
(5)重复上述步骤,直到所有节点都被访问过。
#include<bits/stdc++.h>
using namespace std;void dfs(int u, vector<bool>& visited, vector<vector<int>>& adjList) {visited[u] = true; // 标记节点u为已访问cout << u << " "; // 输出节点u// 遍历所有与节点u相邻的节点for (int v : adjList[u]) {if (!visited[v]) {dfs(v, visited, adjList); // 递归访问节点v}}
}void dfsTraversal(int n, vector<vector<int>>& adjList) {vector<bool> visited(n + 1, false); // 初始化所有节点为未访问状态for (int i = 1; i <= n; i++) {if (!visited[i]) { // 如果节点i未被访问过,从节点i开始DFS遍历dfs(i, visited, adjList);}}
}int main() {int n, m;cin >> n >> m; // 读入节点数和边数vector<vector<int>> adjList(n + 1); // 邻接表for (int i = 1; i <= m; i++) {int u, v;cin >> u >> v; // 读入一条边的两个端点adjList[u].push_back(v);adjList[v].push_back(u); // 无向图,所以需要两条边}dfsTraversal(n, adjList); // DFS遍历return 0;
}
2. 广度优先搜索(BFS)
广度优先搜索是一种迭代的搜索方式,从一个起点出发,依次访问其所有相邻的节点,并将这些节点加入一个队列中,在队列中按照先进先出的顺序继续访问队列中的节点,直到队列为空为止。具体步骤如下:
(1)访问起点节点,并将其标记为已访问。
(2)将起点节点放入一个队列中。
(3)从队列中取出第一个节点,并访问其所有未被访问的相邻节点,并将这些节点加入队列中。
(4)重复步骤(3),直到队列为空为止。
(5)所有被访问过的节点组成了图的遍历。
#include<bits/stdc++.h>
using namespace std;void bfs(vector<vector<int>>& graph, vector<bool>& visited, int start) {queue<int> q;visited[start] = true;q.push(start);while (!q.empty()) {int curr = q.front();cout << curr << " ";q.pop();for (int neighbor : graph[curr]) {if (!visited[neighbor]) {visited[neighbor] = true;q.push(neighbor);}}}
}int main() {int n = 6; // number of nodes// adjacency list representation of the graphvector<vector<int>> graph(n);graph[0] = {1, 2};graph[1] = {0, 2, 3, 4};graph[2] = {0, 1, 3};graph[3] = {1, 2, 4};graph[4] = {1, 3, 5};graph[5] = {4};// mark all nodes as not visitedvector<bool> visited(n, false);// perform BFS traversal starting from node 0bfs(graph, visited, 0);return 0;
}
相关文章:

图的遍历DFSBFS-有向图无向图
西江月・证明 即得易见平凡,仿照上例显然。留作习题答案略,读者自证不难。 反之亦然同理,推论自然成立。略去过程Q.E.D.,由上可知证毕。 有向图的遍历可以使用深度优先搜索(DFS)和广度优先搜索(…...
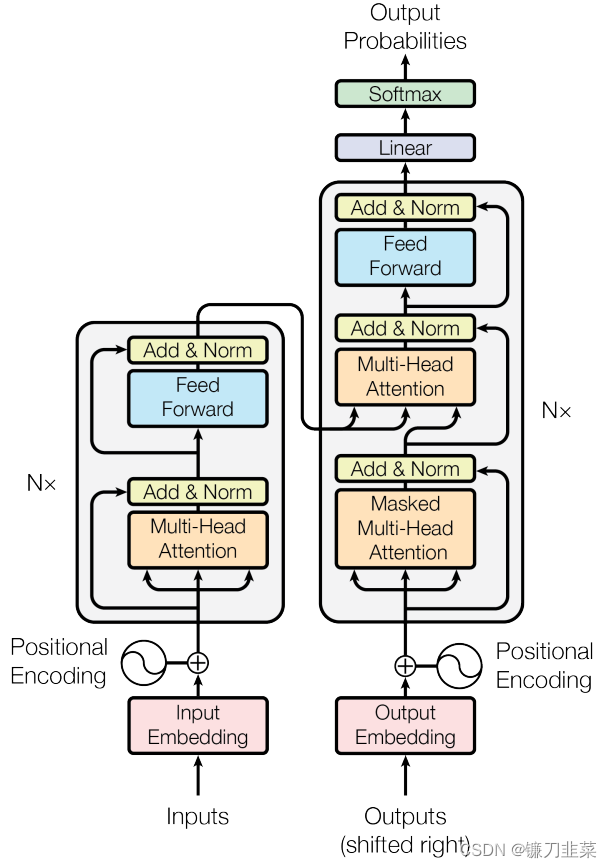
【NLP】深入浅出全面回顾注意力机制
深入浅出全面回顾注意力机制 1. 注意力机制概述2. 举个例子:使用PyTorch带注意力机制的Encoder-Decoder模型3. Transformer架构回顾3.1 Transformer的顶层设计3.2 Encoder与Decoder的输入3.3 高并发长记忆的实现self-attention的矩阵计算形式多头注意力(…...

Linux应用编程的read函数和Linux驱动编程的read函数的区别
Linux应用编程的read函数用于从文件描述符(文件、管道、套接字等)中读取数据。它的原型如下: ssize_t read(int fd, void *buf, size_t count);其中,fd参数是文件描述符,buf是用于存储读取数据的缓冲区,co…...
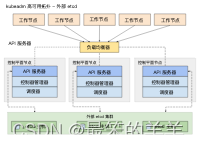
Kubernetes(K8s)从入门到精通系列之十:使用 kubeadm 创建一个高可用 etcd 集群
Kubernetes K8s从入门到精通系列之十:使用 kubeadm 创建一个高可用 etcd 集群 一、etcd高可用拓扑选项1.堆叠(Stacked)etcd 拓扑2.外部 etcd 拓扑 二、准备工作三、建立集群1.将 kubelet 配置为 etcd 的服务管理器。2.为 kubeadm 创建配置文件…...

使用动态规划实现错排问题-2023年全国青少年信息素养大赛Python复赛真题精选
[导读]:超平老师计划推出《全国青少年信息素养大赛Python编程真题解析》50讲,这是超平老师解读Python编程挑战赛真题系列的第15讲。 全国青少年信息素养大赛(原全国青少年电子信息智能创新大赛)是“世界机器人大会青少年机器人设…...

大规模向量检索库Faiss学习总结记录
因为最近要使用到faiss来做检索和查询,所以这里只好抽出点时间来学习下,本文主要是自己最近学习的记录,来源于网络资料查询总结,仅用作个人学习总结记录。 Faiss的全称是Facebook AI Similarity Search,是FaceBook的A…...
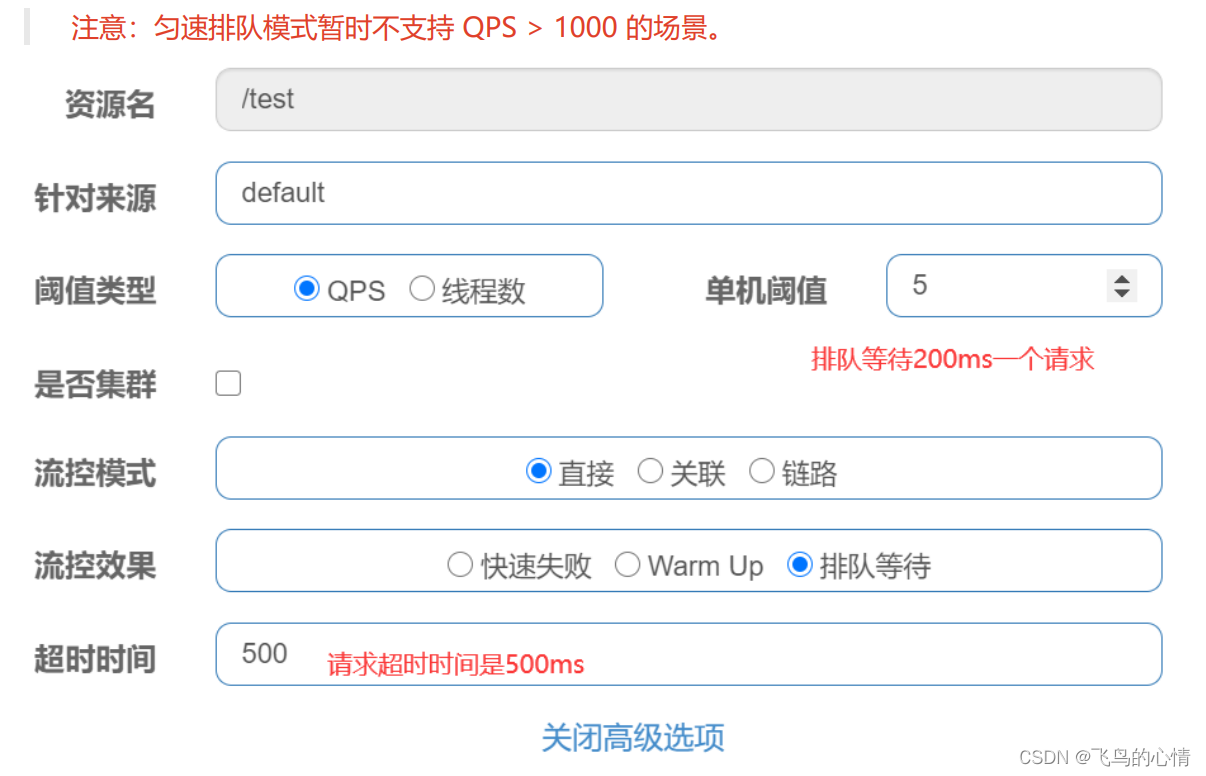
SpringCloudAlibaba之Sentinel(一)流控篇
前言: 为什么使用Sentinel,这是一个高可用组件,为了使我们的微服务高可用而生 我们的服务会因为什么被打垮? 一,流量激增 缓存未预热,线程池被占满 ,无法响应 二,被其他服务拖…...

哪种模式ip更适合你的爬虫项目?
作为一名爬虫程序员,对于数据的采集和抓取有着浓厚的兴趣。当谈到爬虫ip时,你可能会听说过两种常见的爬虫ip类型:Socks5爬虫ip和HTTP爬虫ip。但到底哪一种在你的爬虫项目中更适合呢?本文将帮助你进行比较和选择。 首先,…...
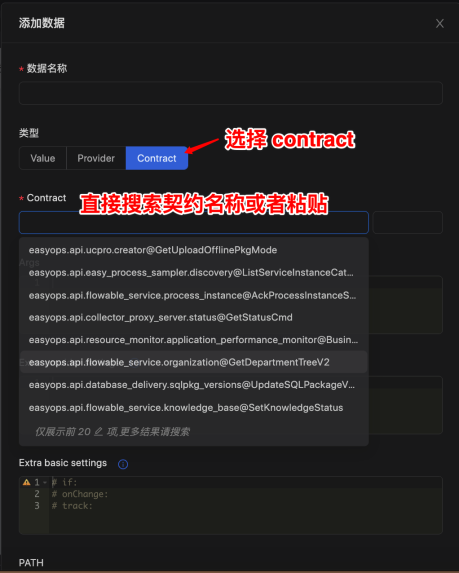
优维低代码实践:对接数据
优维低代码技术专栏,是一个全新的、技术为主的专栏,由优维技术委员会成员执笔,基于优维7年低代码技术研发及运维成果,主要介绍低代码相关的技术原理及架构逻辑,目的是给广大运维人提供一个技术交流与学习的平台。 优维…...

docker 离线模式-部署容器
有网络的情况下下载需要的镜像 比如(下面以tomcat为例子,其他镜像类似) docker pull tomcat打包镜像文件到本地 docker save tomcat -o tomcat.tar将tomcat.tar 上传到内网服务器(无外网环境) 导入镜像 docker load -i tomcat.tar创建容器…...

MDN-HTTP
参考资料 文章目录 HTTP简介HTTP 和 HTTPSHTTP消息典型的HTTP会话HTTP响应状态HTTP安全HTTP CookieHTTP压缩 HTTP简介 HTTP(Hypertext Transfer Protocol)是一种用于在计算机网络中传输超文本和其他资源的应用层协议。他是互联网的基础协议之一&#x…...

【数据库】PostgreSQL中使用`SELECT DISTINCT`和`SUBSTRING`函数实现去重查询
在PostgreSQL中,我们可以使用SELECT DISTINCT和SUBSTRING函数来实现对某个字段进行去重查询。本文将介绍如何使用这两个函数来实现对resource_version字段的去重查询。 1. SELECT DISTINCT语句 SELECT DISTINCT语句用于从表中选择不重复的记录。如果没有指定列名&…...
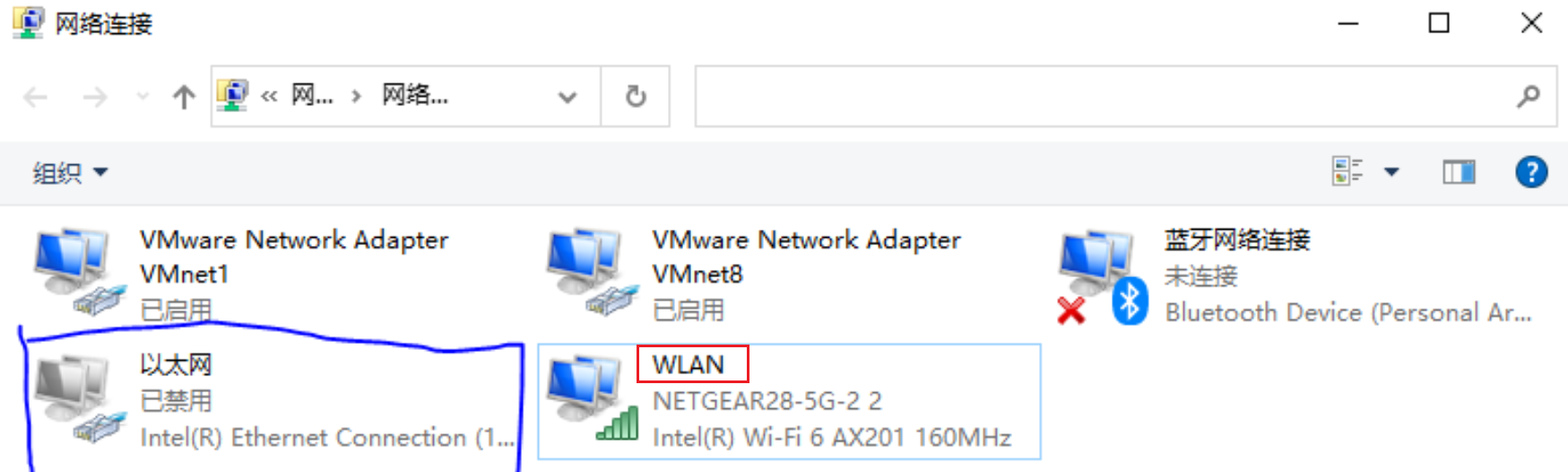
笔记本WIFI连接无网络【实测有效,不用重启电脑】
笔记本Wifi连接无网络实测有效解决方案 问题描述: 笔记本买来一段时间后,WIFI网络连接开机一段时间还正常连接,但是过一段时间显示网络连接不上,重启电脑太麻烦,选择编写重启网络脚本解决。三步解决问题。 解决方案&a…...
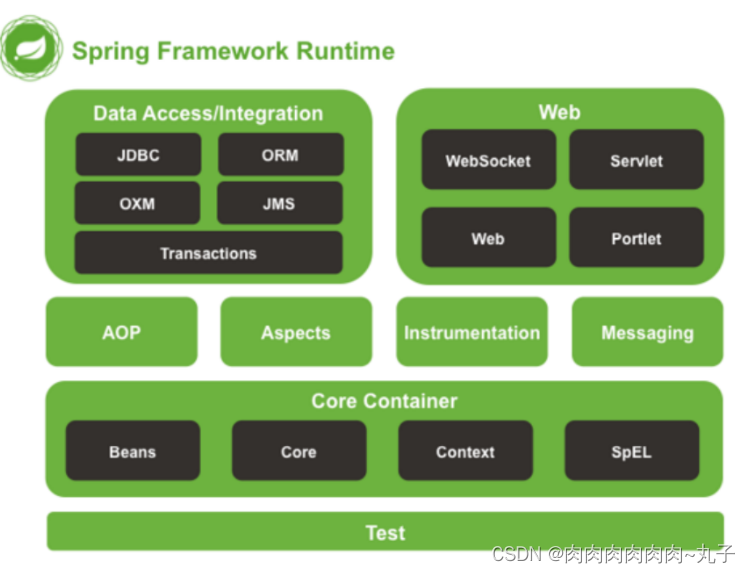
Java课题笔记~ Spring 概述
Spring 框架 一、Spring 概述 1、Spring 框架是什么 Spring 是于 2003 年兴起的一个轻量级的 Java 开发框架,它是为了解决企业应用开发的复杂性而创建的。Spring 的核心是控制反转(IoC)和面向切面编程(AOP)。 Spring…...
2022 robocom 世界机器人开发者大赛-本科组(国赛)
RC-u1 智能红绿灯 题目描述: RC-u1 智能红绿灯 为了最大化通行效率同时照顾老年人穿行马路,在某养老社区前,某科技公司设置了一个智能红绿灯。 这个红绿灯是这样设计的: 路的两旁设置了一个按钮,老年人希望通行马路时会…...

【雕爷学编程】Arduino动手做(195)---HT16k33 矩阵 8*8点阵屏模块6
37款传感器与模块的提法,在网络上广泛流传,其实Arduino能够兼容的传感器模块肯定是不止37种的。鉴于本人手头积累了一些传感器和执行器模块,依照实践出真知(一定要动手做)的理念,以学习和交流为目的&#x…...

Typescript]基础篇之 tsc 命令解析
[Typescript]基础[TOC]([Typescript]基础篇之 tsc 命令解析 tsc 命令概览编译参数说明--declaration--watch 这里是对 tsc 的一个详细介绍 tsc 命令概览 安装 Typescript 后可以使用 tsc 编译 ts 文件,tsc 命令是否支持其它参数 如果需要查看 tsc 支持的命令,或者…...
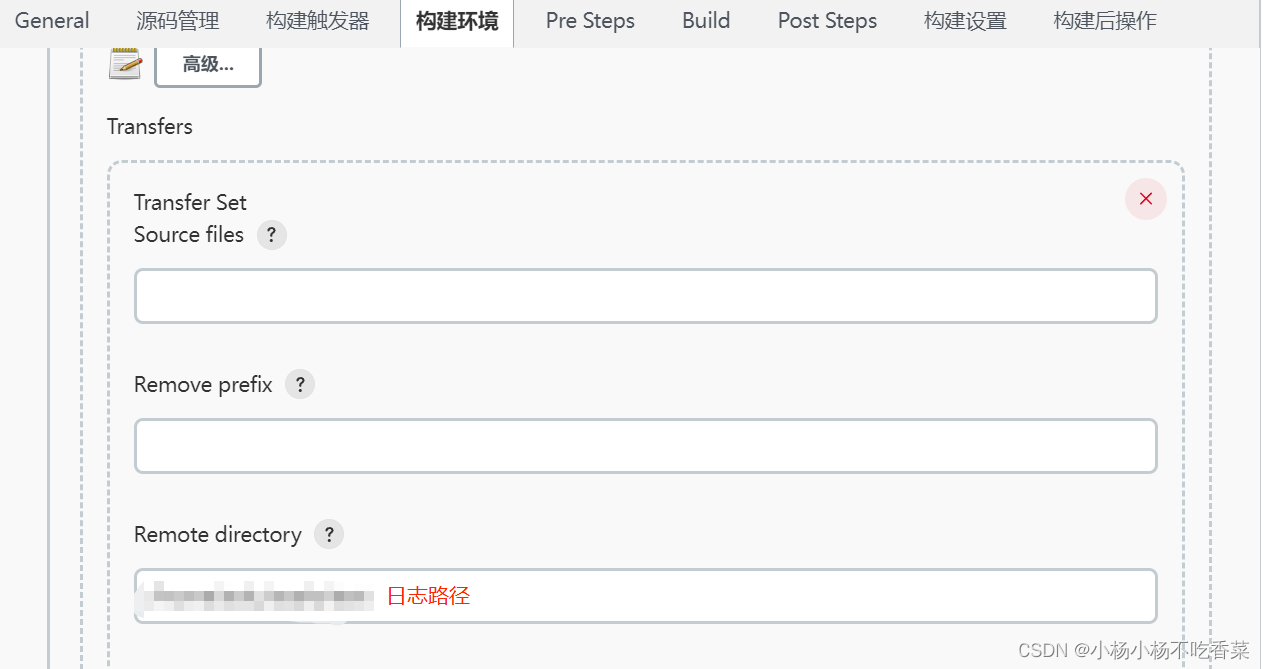
测试人员简单使用Jenkins
一、测试人员使用jenkins干什么? 部署测试环境 二、相关配置说明 一般由开发人员进行具体配置 1.Repository URL:填写git地址 2.填写开发分支,测试人员可通过相应分支进行测试环境的构建部署 当多个版本并行时,开发人员可以通过…...
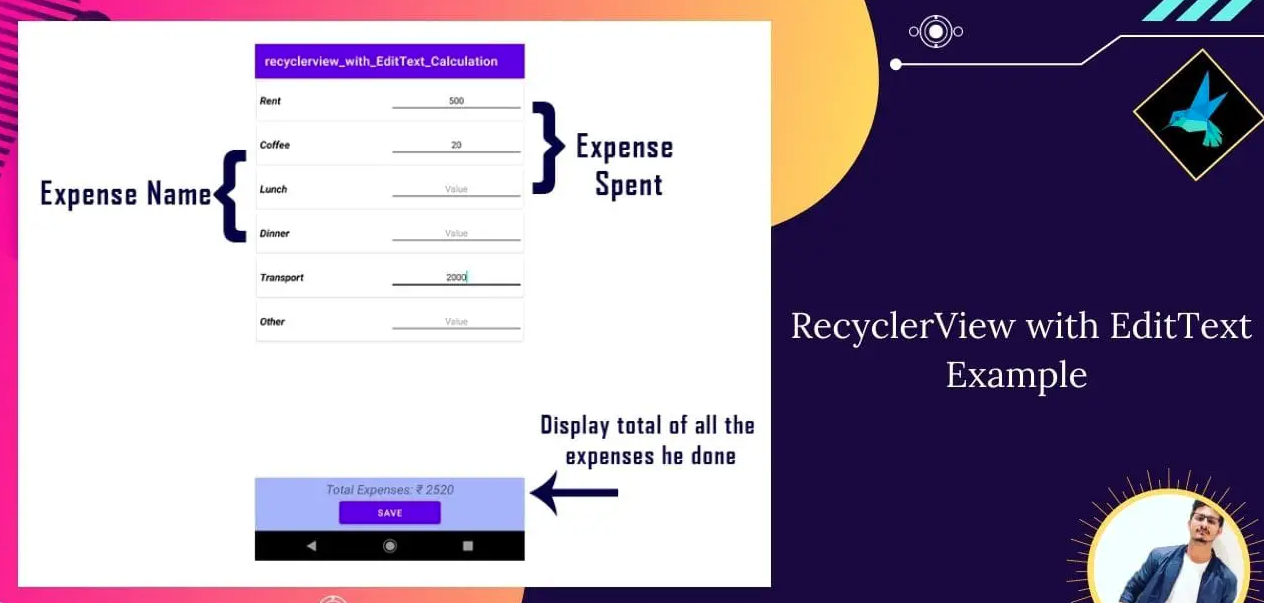
使用RecyclerView构建灵活的列表界面
使用RecyclerView构建灵活的列表界面 1. 引言 在现代移动应用中,列表界面是最常见的用户界面之一,它能够展示大量的数据,让用户可以浏览和操作。无论是社交媒体的动态流、商品展示、新闻列表还是任务清单,列表界面都扮演着不可或…...

linux ubuntu安装mysql
在 Ubuntu 上安装 MySQL 的步骤如下: 更新系统软件包列表: sudo apt update 安装 MySQL 服务器: sudo apt install mysql-server 安装完成,可以使用以下命令检查 MySQL 服务器是否正在运行: sudo systemctl status mysql 如果 MyS…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...
