Leetcode-每日一题【剑指 Offer 13. 机器人的运动范围】
题目
地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。例如,当k为18时,机器人能够进入方格 [35, 37] ,因为3+5+3+7=18。但它不能进入方格 [35, 38],因为3+5+3+8=19。请问该机器人能够到达多少个格子?
示例 1:
输入:m = 2, n = 3, k = 1
输出:3
示例 2:
输入:m = 3, n = 1, k = 0
输出:1
提示:
1 <= n,m <= 1000 <= k <= 20
解题思路
1.题目要求我们求出机器人能够到达多少个格子,对于这道题我们依旧采用深度优先搜索来解决。
2.首先定义一个m行n列的布尔类型的visited数组,用来记录每个格子是否被访问过。然后定义一个dfs方法,用来进行深度优先搜索。在搜索过程中,如果当前格子的行或列小于0,或者大于等于m或n,或者当前格子已经被访问过,或者当前格子的数字之和大于k,则返回0。否则,将当前格子标记为已访问,并返回1加上向右、向下、向左、向上四个方向的dfs调用结果之和。
3.再定义一个sum方法,用来计算一个数字的每一位之和。首先定义一个res变量,并将其初始化为0。然后判断x是否为0,如果不为0,则将res加上x的个位数,并将x除以10。最后返回res。
4.在movingCount方法中,首先初始化类成员变量m、n和k,并创建一个m行n列的visited数组。然后调用dfs方法,从矩阵的左上角开始搜索,并返回结果。
代码实现
class Solution {int m;int n;int k;boolean[][] visited;public int movingCount(int m, int n, int k) {this.m = m;this.n = n;this.k = k;visited = new boolean[m][n];return dfs(0,0);}public int dfs(int i, int j){if(i < 0 || j < 0 || i >= m || j >= n || visited[i][j] || k<sum(i)+sum (j)){return 0;}visited[i][j] = true;return 1 + dfs(i+1,j) + dfs(i,j+1) + dfs(i-1,j) + dfs(i,j-1);}int sum(int x){int res = 0;while(x != 0){res = res +(x % 10);x = x / 10;}return res;}
}测试结果

相关文章:

Leetcode-每日一题【剑指 Offer 13. 机器人的运动范围】
题目 地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。例…...

WEB集群——负载均衡集群
目录 一、 LVS-DR 群集。 1、LVS-DR工作原理 2、LVS-DR模式的特点 3、部署LVS-DR集群 3.1 配置负载调度器(192.168.186.100) 3.2 第一台web节点服务器(192.168.186.103) 3.3 第二台web节点服务器(192.168.186.…...
ubuntu 20.0.4 搭建nvidia 显卡环境
一、安装docker 1、安装dokcer sudo apt install docker.io2、docker 添加到用户组 创建docker用户组 sudo groupadd docker添加当前用户加入docker用户组 sudo usermod -aG docker ${USER}重启docker服务 sudo systemctl restart docker切换或者退出当前账户再从新登入 …...
Windows环境下通过 系统定时 执行脚本方式 压缩并备份文件夹 到其他数据盘
环境配置 压缩时需要使用7-zip进行调用,因此根据自己电脑进行安装 官网:https://www.7-zip.org/ 脚本文件 新建记事本文件,重命名为git_back_up.bat echo off rem 设置utf-8可以正常显示中文 chcp 65001 > nulrem 获取当前日期和时间&…...

C++系列二:STL教程-常用算法
提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档 常用算法 前言算法列举:算法例子 前言 还有一些我在尝试中迷惑不解的,有点玄幻。 算法列举: 排序算法: sort(first, last);…...

【css】渐变
渐变是设置一种颜色或者多种颜色之间的过度变化。 两种渐变类型: 线性渐变(向下/向上/向左/向右/对角线) 径向渐变(由其中心定义) 1、线性渐变 语法:background-image: linear-gradient(direction, co…...
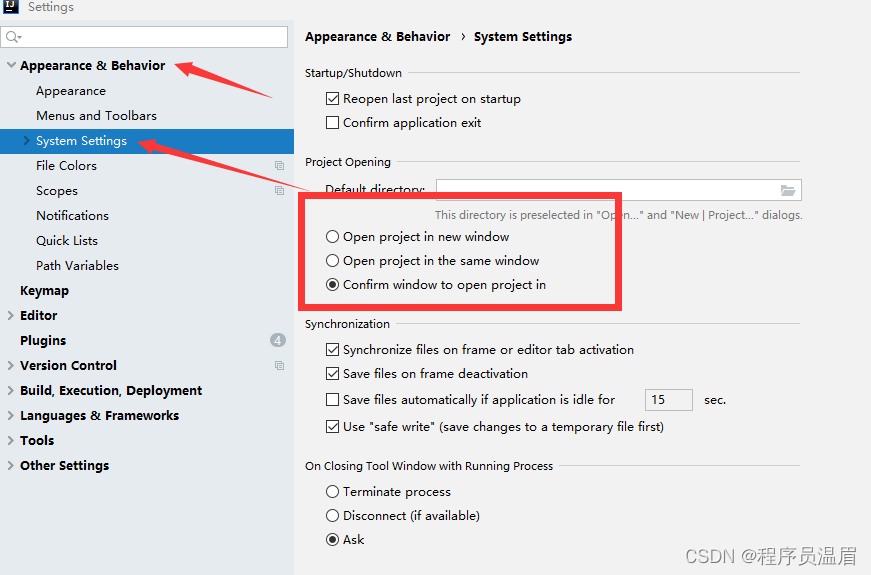
idea打开多个项目需要开多个窗口(恢复询问弹窗)
【版权所有,文章允许转载,但须以链接方式注明源地址,否则追究法律责任】【创作不易,点个赞就是对我最大的支持】 前言 仅作为学习笔记,供大家参考 总结的不错的话,记得点赞收藏关注哦! 使用…...

篇十三:策略模式:选择不同算法
篇十三:“策略模式:选择不同算法” 设计模式是软件开发中的重要知识,策略模式(Strategy Pattern)是一种行为型设计模式,用于在运行时根据不同的需求选择不同的算法或行为。本文将探讨策略模式的作用和实现…...

Centos7.6 安装mysql过程全记录
在centos 7.6上 离线安装mysql 的步骤,可参考下文: 一、查看当前MySQL的安装情况并卸载 1. 查看当前MySQL的安装情况 查找之前是否安装了MySQL rpm -qa|grep -i mysql 2.卸载mysql 如果已经安装mysql,则需要先停止MySQL,再删除…...

Java中的Guava是什么?
Java中的Guava是一个非常强大的Java库,它提供了很多实用的工具类和方法,可以帮助我们更高效地开发Java应用程序。从新手的角度来看,Guava可以让我们在Java编程中变得更加简单、快速和高效。 Guava的命名来源于“Google’s favorite Java lib…...

vue.js兄弟组件方法调用b组件调用a组件方法
vue.js 中兄弟组件方法调用 场景:父组件中同时引入两个子组件(A和B),此时B组件点击按钮需要调用A组件里面的方法 方案1:vue的事件总线 方案2:自定义事件($emit) 最终方案:…...

【Kubernetes】二进制搭建
目录 二进制搭建 Kubernetes v1.20 操作系统初始化配置 关闭防火墙 关闭selinux 关闭swap 根据规划设置主机名 在master添加hosts 调整内核参数 时间同步 部署 etcd 集群 准备签发证书环境 准备cfssl证书生成工具 生成Etcd证书 上传 etcd-cert.sh 和 etcd.sh 到 …...

【MFC】08.MFC消息,自定义消息,常用控件(MFC菜单创建大总结),工具栏,状态栏-笔记
本专栏上几篇文章讲解了MFC几大机制,今天带领大家学习MFC自定义消息以及常用控件,最常用的控件请查看本专栏第一二篇文章,今天这篇文章介绍工具栏,菜单和状态栏,以及菜单创建大总结。 文章目录 MFC消息分类࿱…...

Clickhouse 数据存储
一、数据分区 数据是以分区目录的形式组织的,每个分区独立分开存储.这种形式,查询数据时,可以有效的跳过无用的数据文件。 1.1 数据分区的规则 分区键的取值,生成分区ID,分区根据ID决定。根据分区键的数据类型不同&am…...
c语言每日一练(3)
前言:每日一练系列,每一期都包含5道选择题,2道编程题,博主会尽可能详细地进行讲解,令初学者也能听的清晰。每日一练系列会持续更新,暑假时三天之内必有一更,到了开学之后,将看学业情…...
、File(文件)和IO)
java基础-Stream(流)、File(文件)和IO
Java中的流(Stream)提供了一个统一的接口来处理输入和输出数据,文件(File)提供了一种简单的方式来操作磁盘上的文件,而I/O则允许我们在Java程序中读写数据。 一、流Stream java中得stream是一种抽象概念,流可以从多种来源读取数据ÿ…...
el-table实现指定列合并
table传入span-method方法可以实现合并行或列,方法的参数是一个对象,里面包含当前行row、当前列column、当前行号rowIndex、当前列号columnIndex四个属性。该函数可以返回一个包含两个元素的数组,第一个元素代表rowspan,第二个元素…...
38.利用matlab解 有约束无约束的参数估计对比(matlab程序)
1.简述 1.离散型随机变量的极大似然估计法: (1) 似然函数 若X为离散型, 似然函数为 (2) 求似然函数L(θ)的最大值点 θ, 则θ就是未知参数的极大似然估计值. 2.连续型随机变量的极大似然估计法: (1) 似然函数 若 X 为连续型, 似然函数为 (2) 求似然函数L(θ)的最大值点θ, 则…...
什么是React?React与VU的优缺点有哪些?
什么是React?什么是VUE? 维基百科上的概念解释,Vue.js是一个用于创建用户界面的开源MVVM前端JavaScript框架,也是一个创建单页应用的Web应用框架。Vue.js由尤雨溪(Evan You)创建,由他和其他活跃…...

区块链技术助力慈善,为您的善举赋予全新力量!
我们怀揣着一颗温暖的心,秉承着公开透明的理念,带着信任与责任,倾力打造了一套区块链技术驱动的去中心化捐赠与物资分发系统,通过智能生态网络(IEN)解决捐赠不透明问题的系统,让您的善举直接温暖…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...
