Distance 2023牛客暑期多校训练营6 B
登录—专业IT笔试面试备考平台_牛客网
题目大意:给出两个长度为n的数组a,b,每次操作可以令一个数+1,将a的一个子集A变成和b的一个子集B变成完全相同需要的最少操作数为C(A,B),求对于a的所有子集对所有b的子集的C(A,B)的和
1<=n<=2e3
思路:我们先考察对于整个数组,如何操作使其操作数最少,首先我们需要将数字两两配对,然后分别将每一对数字变成一样的,要想整个数组求出来的最少,每一对数字之间的差就应该最小,所以最优操作就是将整个数组排序。
然后发现最大的时间复杂度是n方,显然不能枚举所有几何,但我们可以枚举每一对数字,因为根据我们上面得出的策略,在每个集合中操作的数对都是相同的,所以我们可以求每一对数组需要的操作数*含有这个数对的集合数量假设我们在长度为7的数组中选中了a[3],b[4],那么根据范德蒙德卷积公式(acm数学(番外1) 范德蒙德卷积公式_Chmaz的博客-CSDN博客)包含他们的区间数就是C(2,2+3)*C(3,3+4),对答案求和即可
//#include<__msvc_all_public_headers.hpp>
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e3 + 5;
int a[N], b[N];
ll inv[N*2], fac[N*2];
const ll MOD = 998244353;
ll qpow(ll a, ll b)
{a %= MOD;ll ret = 1;while (b){if (b & 1){ret = ret * a % MOD;}a = a * a % MOD;b >>= 1;}return ret;
}
ll C(ll x, ll y)
{return fac[y] * inv[x] % MOD * inv[y - x] % MOD;
}
int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int n;cin >> n;fac[0] = inv[0] = 1;for (int i = 1; i <= 2 * n; i++){fac[i] = fac[i - 1] * i % MOD;inv[i] = qpow(fac[i], MOD - 2);}for (int i = 1; i <= n; i++){cin >> a[i];}for (int i = 1; i <= n; i++){cin >> b[i];}sort(a + 1, a + n + 1);sort(b + 1, b + n + 1);ll ans = 0;for (ll i = 1; i <= n; i++){for (ll j = 1; j <= n; j++){ans = (ans + abs(a[i] - b[j]) * C(min(i - 1, j - 1), i-1 + j-1) % MOD * C(min(n - i, n - j), n - i + n - j) % MOD) % MOD;}}cout << ans << endl;return 0;
}相关文章:

Distance 2023牛客暑期多校训练营6 B
登录—专业IT笔试面试备考平台_牛客网 题目大意:给出两个长度为n的数组a,b,每次操作可以令一个数1,将a的一个子集A变成和b的一个子集B变成完全相同需要的最少操作数为C(A,B),求对于a的所有子集对所有b的子集的C(A,B)的…...
、agg()、transform())
【Pandas】学习笔记之groupby()、agg()、transform()
在数据分析过程中经常需要对数据集进行分组,并且统计均值,最大值等等。那么 groupby() 的学习就十分有必要了 groupby(): 分组 官方文档: DataFrame.groupby(byNone, axis0, levelNone, as_indexTrue, sortTrue, group_keysTrue, observedF…...

使用正则表达式 移除 HTML 标签后得到字符串
需求分析 后台返回的数据是 这样式的 需要讲html 标签替换 high_light_text: "<span stylecolor:red>OPPO</span> <span stylecolor:red>OPPO</span> 白色 01"使用正则表达式 function stripHTMLTags(htmlString) {return htmlString.rep…...
Java中String方法魔性学习
这里写目录标题 先进行专栏介绍String详解常用构造方法代码演示常用成员方法代码示例总结 先进行专栏介绍 本专栏是自己学Java的旅途,纯手敲的代码,自己跟着黑马课程学习的,并加入一些自己的理解,对代码和笔记 进行适当修改。希望…...
Smartbi 权限绕过漏洞复现(QVD-2023-17461)
0x01 产品简介 Smartbi大数据分析产品融合BI定义的所有阶段,对接各种业务数据库、数据仓库和大数据分析平台,进行加工处理、分析挖掘和可视化展现;满足所有用户的各种数据分析应用需求,如大数据分析、可视化分析、探索式分析、复杂…...

springboot自定义错误消息
为了提供自定义错误消息提示,springboot在resources目录下,有一个文件ValidationMessages.properties 用于存储 验证错误的消息提示: 比如: 这样一个ValidationMessage.properties username.notempty用户名不能为空 username.len…...
微信小程序申请步骤
微信公众平台链接:https://mp.weixin.qq.com/ 1、进到微信公众平台,点一下“点击注册”,挑选账号申请种类“小程序”,填好微信小程序用户信息,包含电子邮箱、登陆密码等。 2、微信公众平台会发送一封电子邮件…...

嘉楠勘智k230开发板上手记录(四)--HHB神经网络模型部署工具
按照K230_AI实战_HHB神经网络模型部署工具.md,HHB文档,RISC-V 编译器和模拟器安装来 一、环境 1. 拉取docker 镜像然后创建docker容器并进入容器 docker pull hhb4tools/hhb:2.4.5 docker run -itd --namehhb2_4 -p 22 "hhb4tools/hhb:2.4.5"…...
微信小程序的自定义TabBar及Vant的使用
一、安装Vant 1、在 资源管理器 空白位置,点右键打开 在外部终端窗口打开 2、初始化NPM npm init -y 3、安装命令 npm i vant/weapp1.3.3 -S --production 4、构建NPM包 在 工具 里选择构建NPM包 5、删除style:v2 在app.json里,删除"style"…...
canvas实现代码雨
学习抖音: 渡一前端必修课 效果图: 全部代码: <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge">&…...
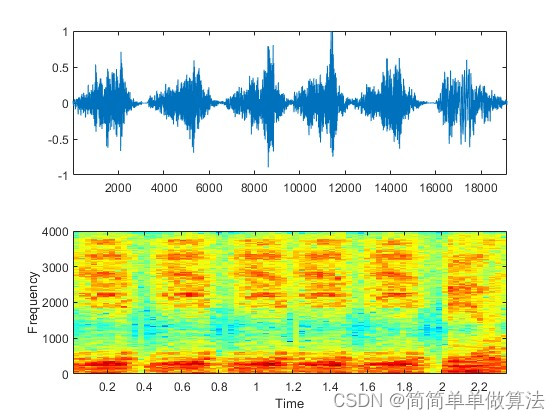
基于MFCC特征提取和HMM模型的语音合成算法matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 matlab2022A 3.部分核心程序 ............................................................................ %hmm是已经…...

多重网格算法的cuda编程
这里写自定义目录标题 多重网格算法介绍问题描述——五点差分法求解二维泊松方程五点差分法Gauss迭代算法限制算子介绍提升算子二重网格算法多重网格算法多重网格cuda代码编写串行代码mg.c两重网格cuda并行代码jacobi迭代的cuda编程device_jacobiMakefilecuda_mg.cucuda_mg.hma…...
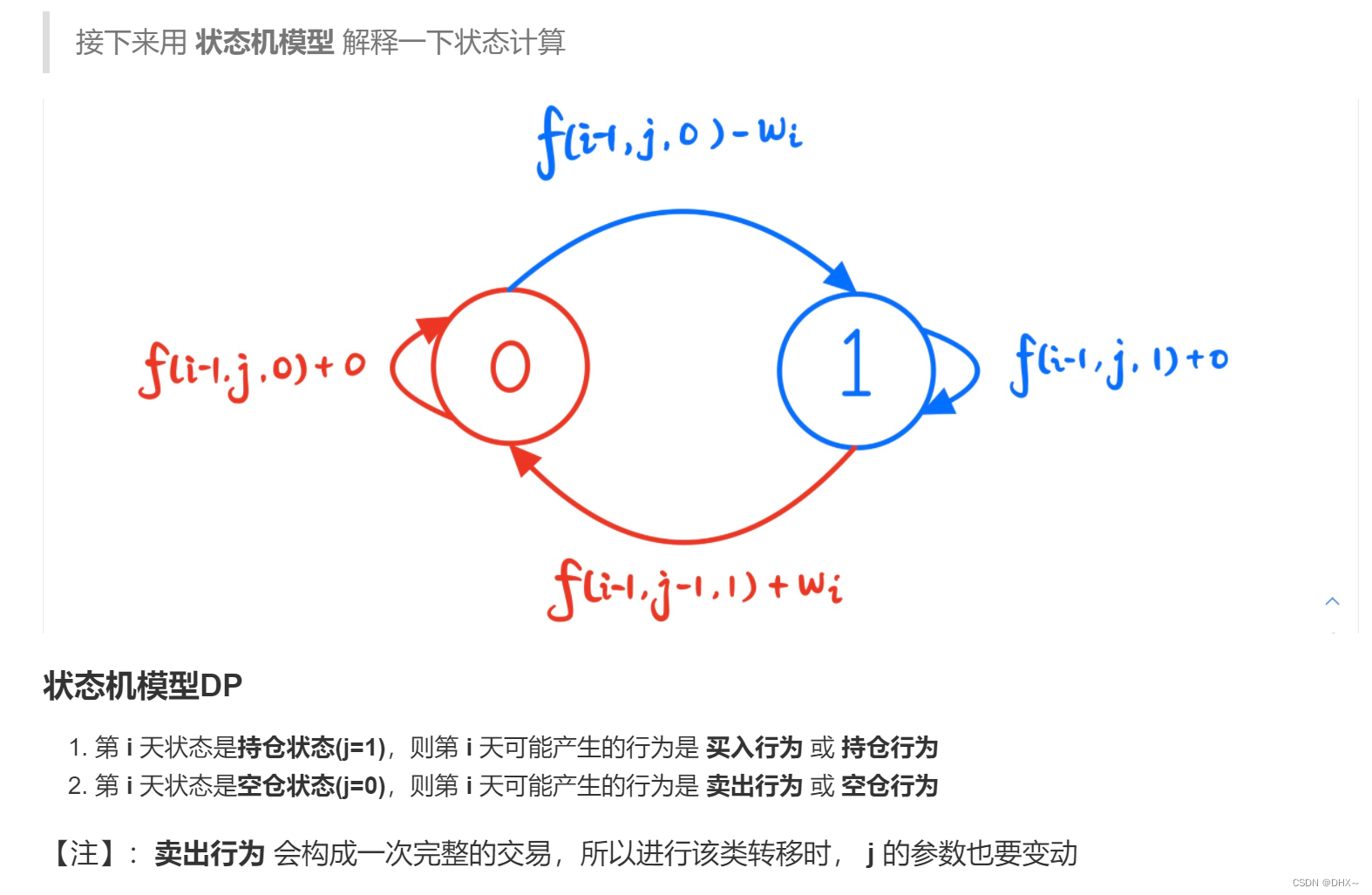
DP(状态机模型)
大盗阿福 阿福是一名经验丰富的大盗。趁着月黑风高,阿福打算今晚洗劫一条街上的店铺。 这条街上一共有 N 家店铺,每家店中都有一些现金。 阿福事先调查得知,只有当他同时洗劫了两家相邻的店铺时,街上的报警系统才会启动&#x…...

按照指定的文件顺序进行scp传输
前言 scp 默认传输顺序是按照文件名进行排序的, 但我当前工作中遇到要验证两台机器的神经网络层的精度,需要把网络层的输入输出(假设有100层, 一共64G) 从机器1传输到机器2 , 然后进行对比;这种情况下最好…...

小红书数据分析丨现实版模拟人生,这届网友热衷于“云开店”?
近期,小红书出现的一个神秘的热心群体,他们经常活跃在各种小店店主发布的求助帖评论区中,积极地帮助店主出谋划策,寻找小店经营的优化之道,成功帮助小店成功转亏为盈!江湖人称一一云股东。小红书话题#爱上帮…...

休闲卤味强势崛起:卤味零食成为新一代热门美食
随着人们生活水平的提高和消费观念的转变,休闲卤味逐渐成为了人们日常生活中的热门美食。据最新数据显示,2022年,我国卤味市场销售额达到了约2000亿元,预计到2025年将突破3000亿元大关。其中,休闲卤味以每年10%的速度持…...

自除数-C语言
描述 给定两个整数 left 和 right ,返回一个列表,列表的元素是范围 [left, right] 内所有的 自除数。 1 < left < right < 104 自除数 是指可以被它包含的每一位数整除的数,自除数 不允许包含 0 。例如,128 是一个 自除…...
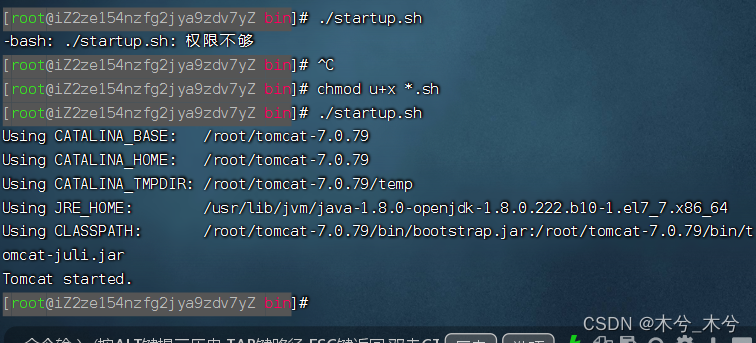
-bash: ./startup.sh: Permission denied解决
今天在Linux上启动Tomcat,结果弹出:-bash: ./startup.sh: Permission denied 的提示。 这是因为用户没有权限,而导致无法执行。用命令chmod 修改一下bin目录下的.sh权限就可以了。 在Tomcat的bin目录下 ,输入命令行 :c…...
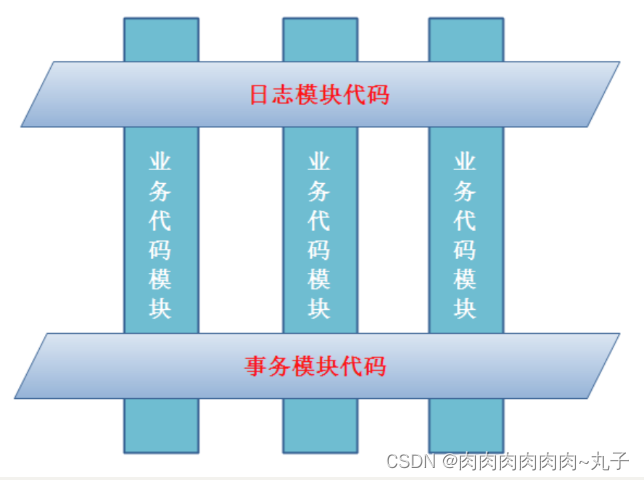
Java课题笔记~ AOP 概述
AOP 简介 AOP(Aspect Orient Programming)面向切面编程。 面向切面编程是从动态角度考虑程序运行过程。 AOP的底层,就是采用动态代理的方式实现的。 采用了两种代理:JDK动态代理、CGLIB动态代理。 JDK动态代理:使…...
真我V3 5G(RMX2200 RMX2201)解锁刷机全过程
安卓系统新Rom包为GSI,更具有通用性,可以比较放心刷。 原厂系统垃圾多、广告多,甚至热点功能不支持ipv6,严重偏离热点机的定位。 主要参考 https://www.bilibili.com/read/cv20730877/https://www.bilibili.com/read/cv2073087…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...
