现代C++中的从头开始深度学习:【4/8】梯度下降
一、说明
在本系列中,我们将学习如何仅使用普通和现代C++编写必须知道的深度学习算法,例如卷积、反向传播、激活函数、优化器、深度神经网络等。
在这个故事中,我们将通过引入梯度下降算法来介绍数据中 2D 卷积核的拟合。我们将使用卷积和上一个故事中引入的成本函数概念,将所有内容编码为现代C++和特征。

这个故事是:C++的梯度下降,查看其他故事:
0 — 现代C++深度学习编程基础
1 — 在C++中编码 2D 卷积
2 — 使用 Lambda 的成本函数
4 — 激活函数
...更多内容即将推出。
二、函数逼近作为优化问题
如果你读过我们之前的演讲,你已经知道,在机器学习中,我们大部分时间都在关注使用数据来寻找函数近似值。
通常,我们通过找到最小化成本值的系数来获得函数近似。因此,我们的近似问题被转换为优化问题,我们试图最小化成本函数的值。
三、成本函数和梯度下降
成本函数计算使用函数 H(X) 近似目标函数 F(X) 的开销。例如,如果 H(X) 是输入 X 和核 k 之间的卷积,则 MSE 成本函数由下式给出:
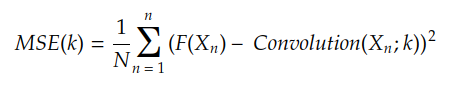
我们通常做 Yn = F(Xn),结果是:
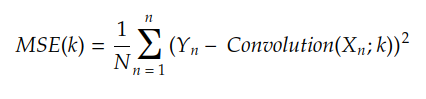
MSE是均方误差,是上一个故事中介绍的成本函数
因此,我们的目标是找到最小化MSE(k)的内核值km。找到 km 的最基本(但最强大)的算法是梯度下降。
梯度下降使用成本函数梯度来查找最小成本。为了理解什么是梯度,让我们谈谈成本表面。
四、绘制成本曲面
为了更容易理解,让我们暂时假设内核仅由两个系数组成。如果我们为每个可能的组合绘制 MSE(k) 的值,我们最终会得到这样的表面:k[k00, k01][k00, k01]

在每个点上,曲面与0k₀₀轴有一个倾角,与0k₀₁轴有另一个倾角:(k00, k01, MSE(k00, k01))
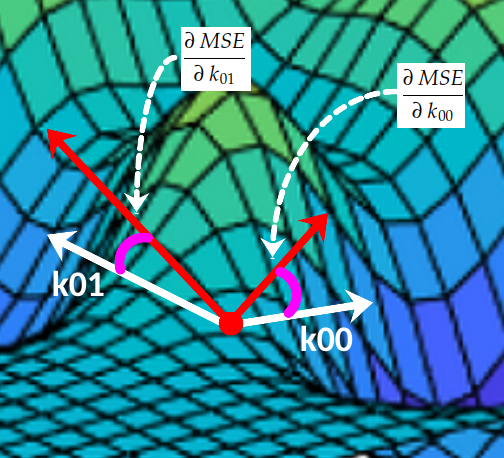
偏导数
这两个斜率分别是 MSE 曲线相对于轴 O k₀₀ 和 Ok₀₁ 的偏导数。在微积分中,我们非常使用符号∂来表示偏导数:
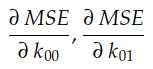
这两个偏导数共同构成了MSE相对于轴O k₀₀和Ok₀₁的梯度。此梯度用于驱动梯度下降算法的执行,如下所示:
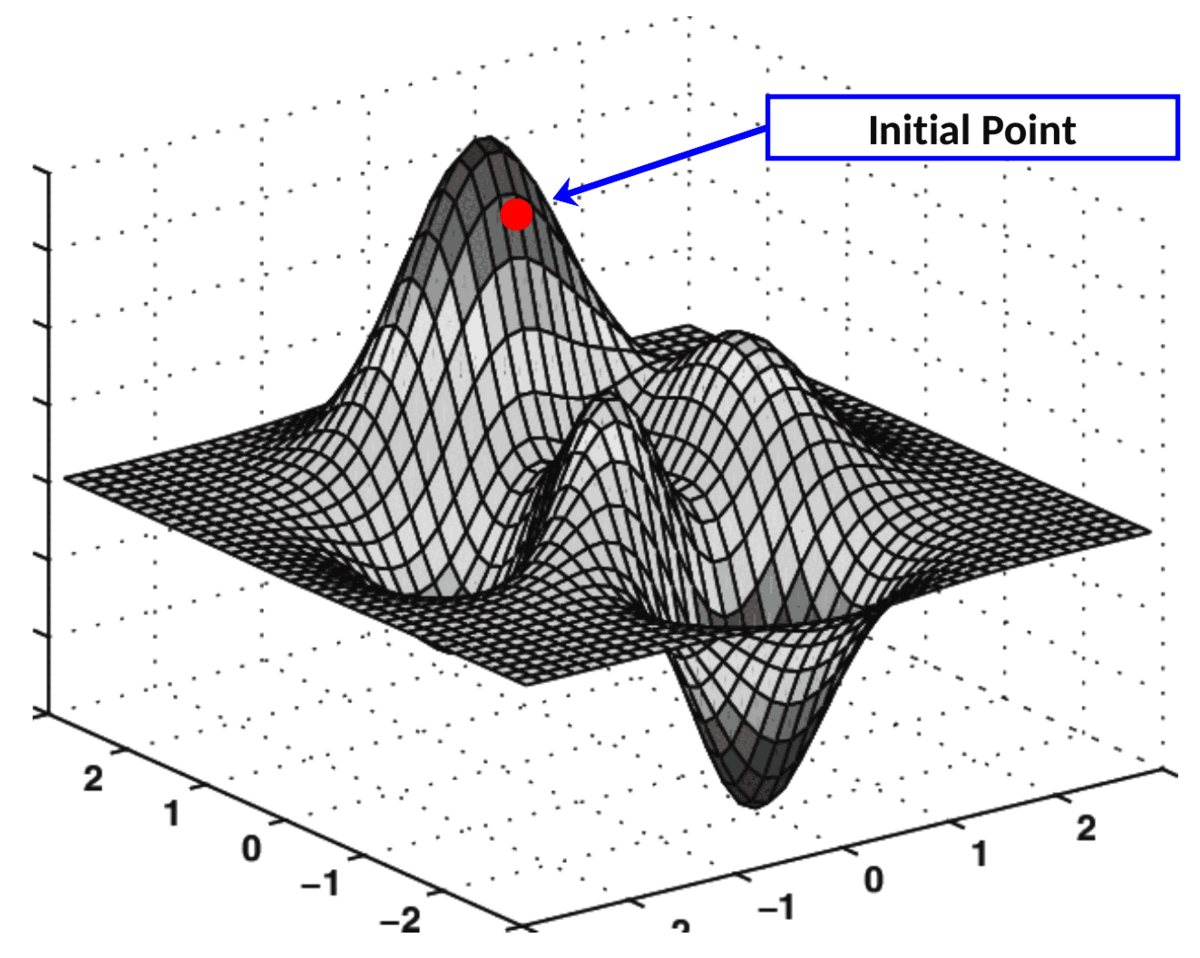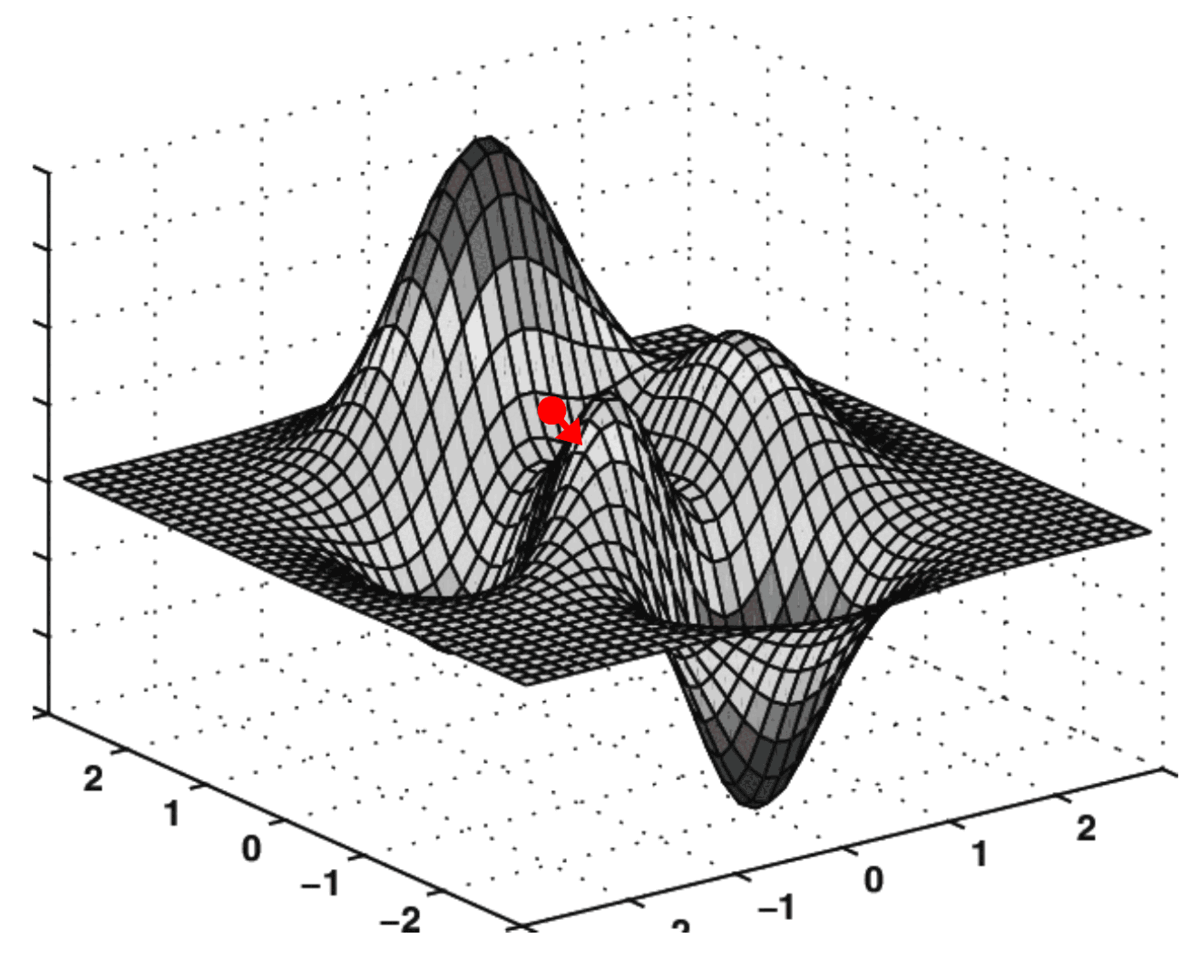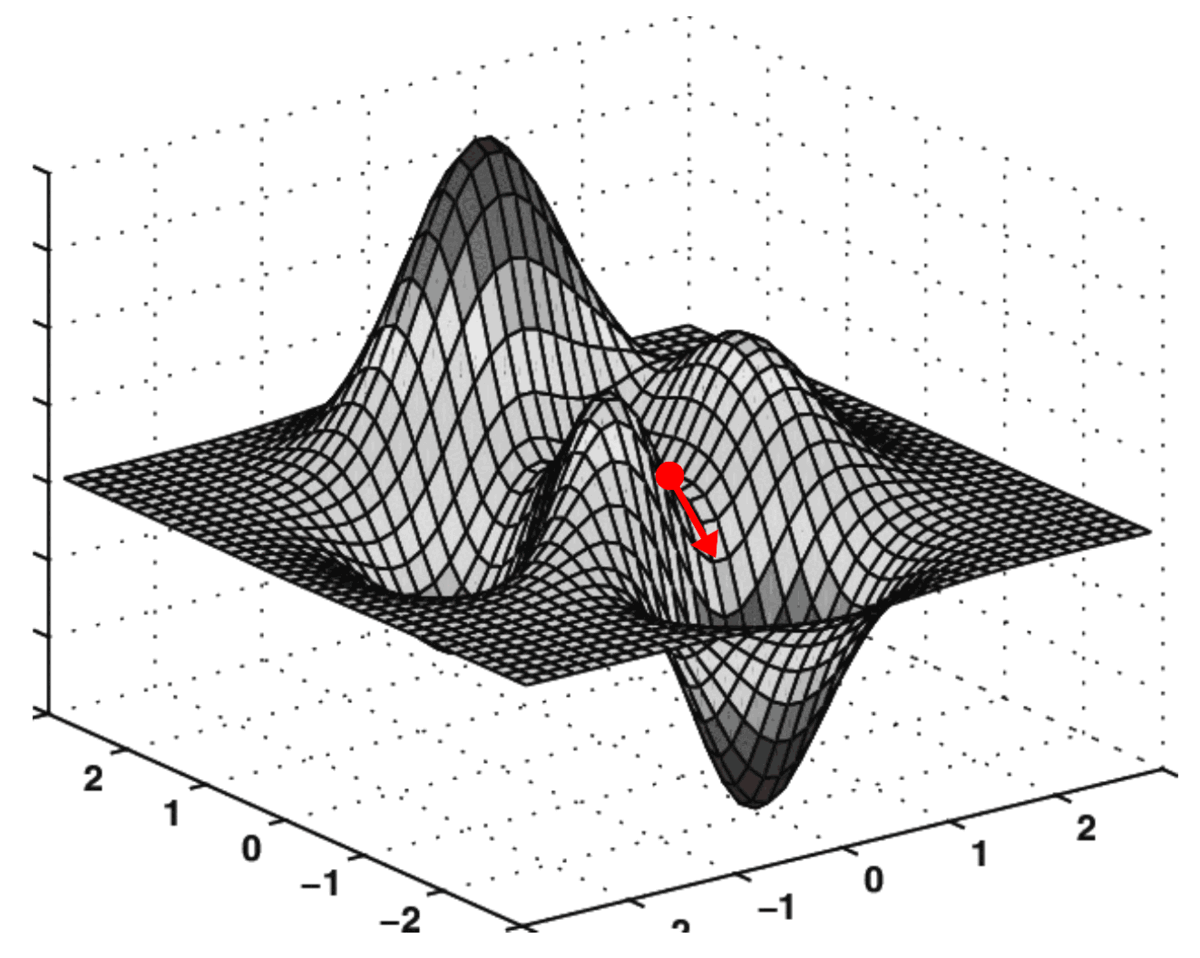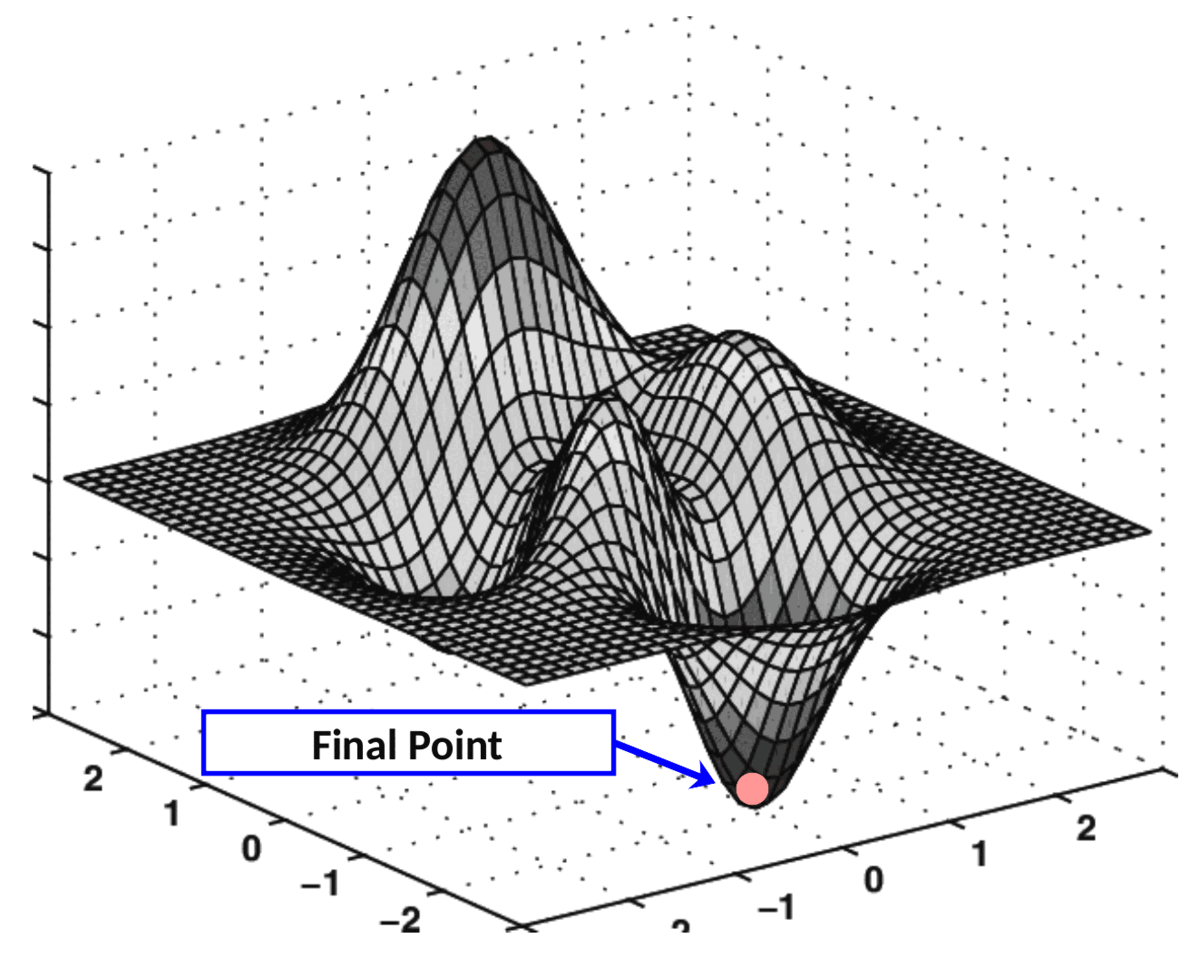
梯度下降的实际应用
在成本表面上执行此“导航”的算法称为梯度下降。
五、梯度下降
梯度下降伪代码描述如下:
gradient_descent:initialize k, learning_rate, epoch = 1repeatk = k - learning_rate x ∇Cost(k)until epoch <= max_epochreturn klearning_rate x ∇Cost(k) 的值通常称为权重更新。我们可以通过以下方式恢复梯度下降的行为:
for each iteration:calculate the weight updatesubtract it from the parameter k顾名思义,Cost(k) 是配置 k 的成本函数。梯度下降的目的是找到成本(k)最小的k值。
learning_rate通常是像 0.1、0.01、0.001 左右这样的标量。此值控制优化过程中的步长。
该算法循环 max_epoch 次。有时,我们会更早地停止算法,即,即使纪元< max_epoch,在 Cost(k) 太小的情况下。
我们通常用超参数的名称来指代learning_rate和max_epoch等参数。
要实现梯度下降,我们需要知道的最后一件事是如何计算 C(k) 的梯度。幸运的是,在成本函数为 MSE 的情况下,如前所述,查找 ∇Cost(k) 非常简单。
六、查找 MSE 梯度
到目前为止,我们已经看到梯度的分量是每个轴 0kij 的成本面的斜率。我们还看到,MSE(k) 相对于每个 i 个、核 k 的系数 j-的梯度由下式给出:
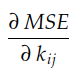
让我们记住,MSE(k) 由下式给出:
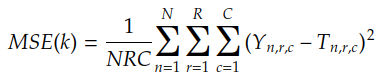
其中n是每对的索引(Yn,Tn),r&c是输出矩阵系数的索引:
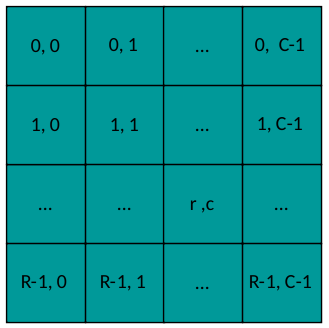
输出布局
使用链式规则和线性组合规则,我们可以通过以下方式找到MSE梯度:
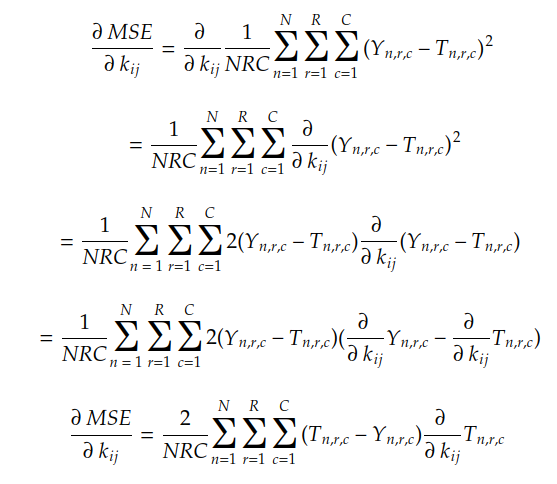
由于 N、R、C、Yn 和 T n 的值是已知的,我们需要计算的只是 Tn 中每个系数相对于系数 kij 的偏导数。在带有填充 P 的卷积的情况下,此导数由下式给出:
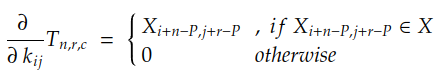
如果我们展开 r 和 c 的总和,我们可以发现梯度由下式给出:
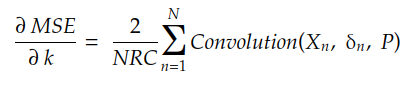
其中 δn 是矩阵:
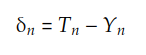
以下代码实现此操作:
auto gradient = [](const std::vector<Matrix> &xs, std::vector<Matrix> &ys, std::vector<Matrix> &ts, const int padding)
{const int N = xs.size();const int R = xs[0].rows();const int C = xs[0].cols();const int result_rows = xs[0].rows() - ys[0].rows() + 2 * padding + 1;const int result_cols = xs[0].cols() - ys[0].cols() + 2 * padding + 1;Matrix result = Matrix::Zero(result_rows, result_cols);for (int n = 0; n < N; ++n) {const auto &X = xs[n];const auto &Y = ys[n];const auto &T = ts[n];Matrix delta = T - Y;Matrix update = Convolution2D(X, delta, padding);result = result + update;}result *= 2.0/(R * C);return result;
};现在我们知道了如何获得梯度,让我们来实现梯度下降算法。
七、编码梯度下降
最后,我们的梯度下降的代码在这里:
auto gradient_descent = [](Matrix &kernel, Dataset &dataset, const double learning_rate, const int MAX_EPOCHS)
{std::vector<double> losses; losses.reserve(MAX_EPOCHS);const int padding = kernel.rows() / 2;const int N = dataset.size();std::vector<Matrix> xs; xs.reserve(N);std::vector<Matrix> ys; ys.reserve(N);std::vector<Matrix> ts; ts.reserve(N);int epoch = 0;while (epoch < MAX_EPOCHS){xs.clear(); ys.clear(); ts.clear();for (auto &instance : dataset) {const auto & X = instance.first;const auto & Y = instance.second;const auto T = Convolution2D(X, kernel, padding);xs.push_back(X);ys.push_back(Y);ts.push_back(T);}losses.push_back(MSE(ys, ts));auto grad = gradient(xs, ys, ts, padding);auto update = grad * learning_rate;kernel -= update;epoch++;}return losses;
};This is the base code. We can improve it in several ways, for example:
- using the loss of each instance to update the kernel. This is called Stochastic Gradient Descent (SGD), which is very useful in real-world scenarios;
- grouping instances in batches and updating the kernel after each batch, which is called Minibatch;
- 使用学习率时间表来降低各个时期的学习率;
- 在这一行中,我们可以连接一个优化器,如Momentum、RMSProp或Adam。 我们将在接下来的故事中讨论优化器;
kernel -= update; - 引入验证集或使用某些交叉验证架构;
- 通过矢量化替换嵌套循环以获得性能和 CPU 使用率(如上一个故事所述);
for(auto &instance: dataset) - 添加回调和钩子以更轻松地自定义我们的训练循环。
我们可以暂时忘记这些改进。现在,重点是了解如何使用梯度来更新参数(在我们的例子中是内核)。这是当今机器学习的基本、核心概念,也是推进更高级主题的关键因素。
让我们通过说明性实验将其付诸行动,看看这段代码是如何工作的。
八、实际实验:修复索贝尔边缘探测器
在上一个故事中,我们了解到我们可以应用 Sobel 滤波器 Gx 来检测垂直边缘:
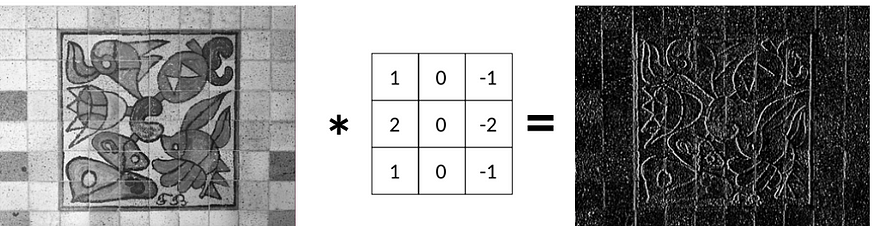
现在,问题是:给定原始图像和边缘图像,我们是否设法恢复了 Sobel 滤镜 Gx?

换句话说,我们可以在给定输入 X 和预期输出 Y 的情况下拟合内核吗?
答案是肯定的,我们将使用梯度下降来做到这一点。
九、加载和准备数据
首先,我们使用OpenCV从文件夹中读取一些图像。我们对它们应用 Gx 过滤器,并将它们成对存储在我们的数据集对象中:
auto load_dataset = [](std::string data_folder, const int padding) {Dataset dataset;std::vector<std::string> files;for (const auto & entry : fs::directory_iterator(data_folder)) {Mat image = cv::imread(data_folder + entry.path().c_str(), cv::IMREAD_GRAYSCALE);Mat formatted_image = resize_image(image, 640, 640);Matrix X;cv::cv2eigen(formatted_image, X);X /= 255.;auto Y = Convolution2D(X, Sobel.Gx, padding);auto pair = std::make_pair(X, Y);dataset.push_back(pair);}return dataset;
};auto dataset = load_dataset("../images/");我们使用辅助实用程序 .resize_image 格式化每个输入图像以适合 640x640 网格

如上图所示,将每个图像集中到黑色 640x640 网格中,而无需通过简单地调整图像大小来拉伸图像。resize_image
我们使用 Gx 过滤器为每个图像生成真实输出 Y。现在,我们可以忘记这个过滤器了。我们将使用梯度下降和 2D 卷积从数据中恢复它。
十、运行实验
通过连接所有部分,我们最终可以看到训练执行情况:
int main() {const int padding = 1;auto dataset = load_dataset("../images/", padding);const int MAX_EPOCHS = 1000;const double learning_rate = 0.1;auto history = gradient_descent(kernel, dataset, learning_rate, MAX_EPOCHS);std::cout << "Original kernel is:\n\n" << std::fixed << std::setprecision(2) << Sobel.Gx << "\n\n";std::cout << "Trained kernel is:\n\n" << std::fixed << std::setprecision(2) << kernel << "\n\n";plot_performance(history);return 0;
}The following sequence illustrates the fitting process:

一开始,内核充满了随机数。因此,在第一个纪元中,输出图像通常是黑色输出。
然而,在几个纪元之后,梯度下降开始使核拟合到全局最小值。
最后,在最后一个纪元中,输出几乎等于基本事实。此时,损失值渐近移动到最低值。让我们检查一下各时期的损失表现:
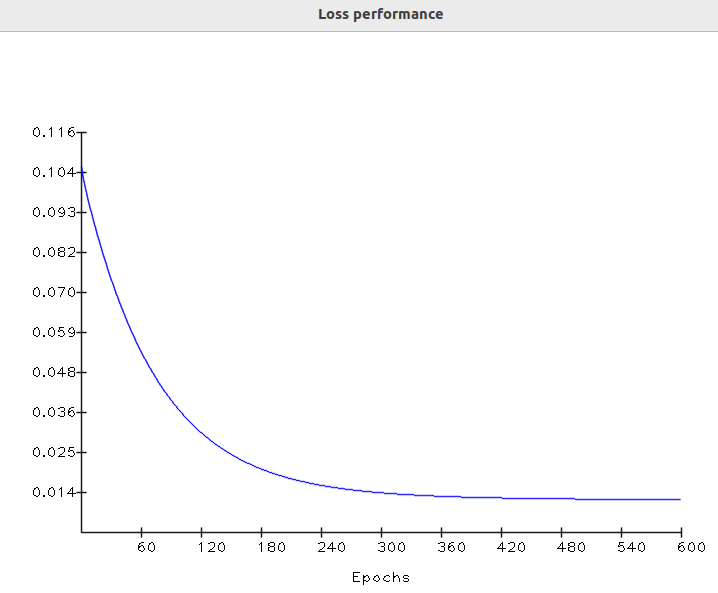
训练表现
在机器学习中,这种损失曲线形状非常常见。事实证明,在第一个纪元中,参数基本上是随机值。这会导致初始损失很高:

成本面上的算法搜索表示
在最后一个时期,梯度下降终于完成了它的工作,将核拟合到合适的值,这使得损失收敛到最小值。
现在,我们可以将学习到的内核与原始 Gx Sobel 的过滤器进行比较:
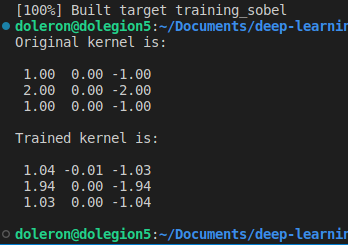
正如我们所料,学习内核和原始内核非常接近。请注意,如果我们在更多的时期训练内核(并使用较小的学习率),这种差异仍然可以更小。
用于训练此内核的代码可以在此存储库中找到。
十一、关于差异化和autodiff
在这个故事中,我们使用常见的微积分规则来查找MSE偏导数。然而,在某些情况下,为给定的复数成本函数找到代数导数可能具有挑战性。幸运的是,现代机器学习框架提供了一个神奇的功能,称为自动微分或简称。autodiff
autodiff跟踪每个基本算术运算(如加法或乘法),将链式规则应用于它们以找到偏导数。因此,在使用时,我们不需要计算偏导数的代数公式,甚至不需要直接实现它们。autodiff
由于这里我们使用的是简单的、众所周知的成本公式,因此不需要手动使用甚至解决复杂的微分。autodiff
更详细地涵盖导数、偏导数和自动微分值得一个新的故事!
十二、结论
在这个故事中,我们学习了如何使用梯度来拟合数据中的内核。我们介绍了梯度下降,它简单、强大,是推导出更复杂的算法(如反向传播)的基础。我们还使用梯度下降法进行了一项实际实验,从数据中恢复了Sobel滤波器。
参考书
机器学习,米切尔
Cálculo 3, Geraldo Ávila(巴西葡萄牙语)
神经网络:综合基础,Haykin
模式分类,杜达
计算机视觉:算法和应用,Szeliski。
Python machine learning, Raschka
相关文章:

现代C++中的从头开始深度学习:【4/8】梯度下降
一、说明 在本系列中,我们将学习如何仅使用普通和现代C编写必须知道的深度学习算法,例如卷积、反向传播、激活函数、优化器、深度神经网络等。 在这个故事中,我们将通过引入梯度下降算法来介绍数据中 2D 卷积核的拟合。我们将使用卷积和上一个…...
Yolov5缺陷检测/目标检测 Jetson nx部署Triton server
使用AI目标检测进行缺陷检测时,部署到Jetson上即小巧算力还高,将训练好的模型转为tensorRT再部署到Jetson 上供http或GRPC调用。1 Jetson nx 刷机 找个ubuntu 系统NVIDIA官网下载安装Jetson 的sdkmanager一步步刷机即可。 本文刷的是JetPack 5.1, 其中包…...
MobaXterm 中文乱码, 及pojie
中文解决方法: 把“连字”去掉! MobaXterm网页,可以生成一个授权文件Custom.mxtpro。放在安装目录就可以了 MobaXterm Keygen (husbin.top)http://b70.husbin.top:5000/...
java: 程序包sun.misc不存在
启动失败,rebuild时也报错:java: 程序包sun.misc不存在 问题出在JDK版本上,这个包在JDK9的时候已经被弃用了,这里改回JDK8即可 步骤如下:...
)
WSL2Linux 子系统(五)
WLS2Linux 子系统编译 Android 上一篇文章中讲解 《WLS2Linux 子系统迁移/恢复》,从C盘迁移到D盘。既可以防止C盘爆红,又可以释放磁盘空间。有更大存储空间意味大有可为,比如说编译Android系统。本文则以开源 firefly Android10代码为例简单…...
java 企业工程管理系统软件源码 自主研发 工程行业适用 em
工程项目管理软件(工程项目管理系统)对建设工程项目管理组织建设、项目策划决策、规划设计、施工建设到竣工交付、总结评估、运维运营,全过程、全方位的对项目进行综合管理 工程项目各模块及其功能点清单 一、系统管理 1、数据字典&#…...
IPO观察丨困于门店扩张的KK集团,还能讲好增长故事吗?
KK集团发起了其IPO之路上的第三次冲击。 近日,KK集团更新了招股书,继续推进港交所上市进程,此前两次上市搁置后终于有了新动向。从更新内容来看,KK集团招股书披露了公司截至2023年一季度的最新业绩,交出一份不错的“成…...
【iOS】RunLoop
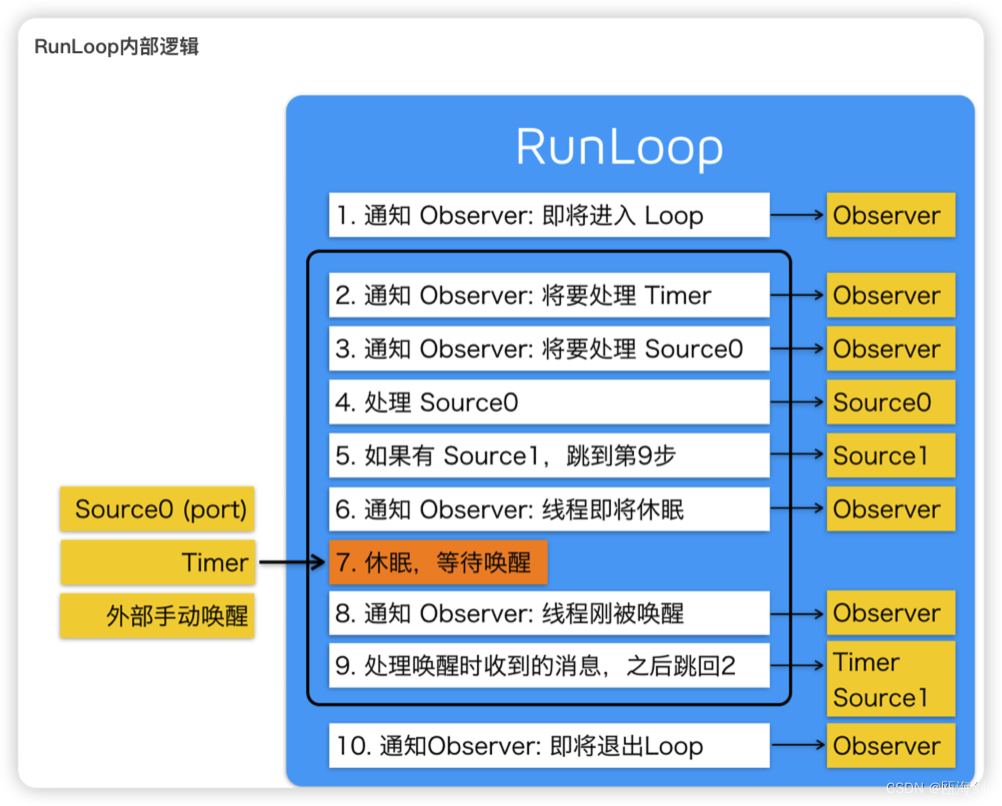
前言-什么是RunLoop? 什么是RunLoop? 跑圈?字面上理解确实是这样的。 Apple官方文档这样解释RunLoop RunLoop是与线程息息相关的基本结构的一部分。RunLoop是一个调度任务和处理任务的事件循环。RunLoop的目的是为了在有工作的时候让线程忙起来&#…...

数据包传输方式:单播、多播、广播、组播、泛播
数据包传输方式 单播、多播、广播、组播、泛播 网络中假设X代表所有的机器,Y代表X中的一部分机器,Z代表一组机器,1代表一台机器,那么 1:1 那就是单播;1:Y 那就是多播;1࿱…...
WebRTC基础知识
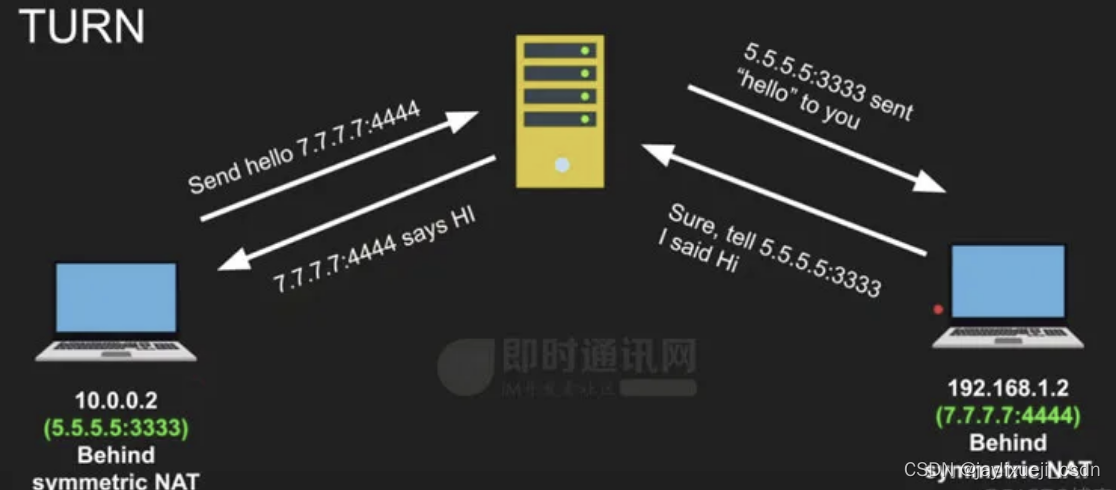
文章目录 基础概念NAT (Network Address Translation) 打洞STUN(Session Traversal Utilities for NAT)基于STUN协议的DDoS反射攻击 # TODO TURN(Traversal Using Relays around NAT)ICE(Interactive Connectivity Est…...
积累常见的有针对性的python面试题---python面试题001
1.考点列表的.remove方法的参数是传入的对应的元素的值,而不是下标 然后再看remove这里,注意这个是,删除写的那个值,比如这里写3,就是删除3, 而不是下标. remove不是下标删除,而是内容删除. 2.元组操作,元组不支持修改,某个下标的内容 可以问他如何修改元组的某个元素 3.…...

在springboot使用websocket时mapper无法注入
直接上代码 package cn.ujoined.combined.utils;import org.springframework.beans.BeansException; import org.springframework.context.ApplicationContext; import org.springframework.context.ApplicationContextAware; import org.springframework.stereotype.Componen…...

前端加密与解密的几种方式
1.base64加密方式 1. base64是什么? Base64,顾名思义,就是包括小写字母a-z、大写字母A-Z、数字0-9、符号""、"/"一共64个字符的字符集,(另加一个“”,实际是65个字符,至于…...

详解Spring Bean的生命周期
详解Spring Bean的生命周期 Spring Bean的生命周期包括以下阶段: 1. 实例化Bean 对于BeanFactory容器,当客户向容器请求一个尚未初始化的bean时,或初始化bean的时候需要注入另一个尚未初始化的依赖时,容器就会调用createBean进…...

详解Shell 脚本中 “$” 符号的多种用法
通常情况下,在工作中用的最多的有如下几项: $0:Shell 的命令本身 1到9:表示 Shell 的第几个参数 $? :显示最后命令的执行情况 $#:传递到脚本的参数个数 $$:脚本运行的当前进程 ID 号 $*&#…...

Redis如何实现Session存储
在Redis中实现Session存储,主要有两种方式:使用Spring Session和手动存储。 使用Spring Session:Spring Session是Spring框架提供的一个模块,用于简化Session管理,并将Session数据存储到外部数据存储中,如Redis。使用Spring Session,你只需要在Spring Boot项目中添加相应…...

安防视频监控汇聚EasyCVR平台接入Ehome告警,公网快照不显示的原因排查
智能视频监控汇聚平台TSINGSEE青犀视频EasyCVR可拓展性强、视频能力灵活、部署轻快,可支持的主流标准协议有国标GB28181、RTSP/Onvif、RTMP等,以及支持厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等,视频监控管理平台…...

【Springboot】@ComponentScan 详解
文章目录 ComponentScanComponentScan ANNOTATION 和 REGEXComponentScan CUSTOMComponentScan ASSIGNABLE_TYPE ComponentScan ComponentScan 是 Spring 框架中的一个注解,用于自动扫描和注册容器中的组件。 使用 ComponentScan 注解可以告诉 Spring 在指定的包或…...

flask-----信号
安装: flask中的信号使用的是一个第三方插件,叫做blinker。通过pip list看一下,如果没有安装,通过以下命令即可安装blinker: pip install blinker flask其中有内置的信号 template_rendered _signals.signal(temp…...
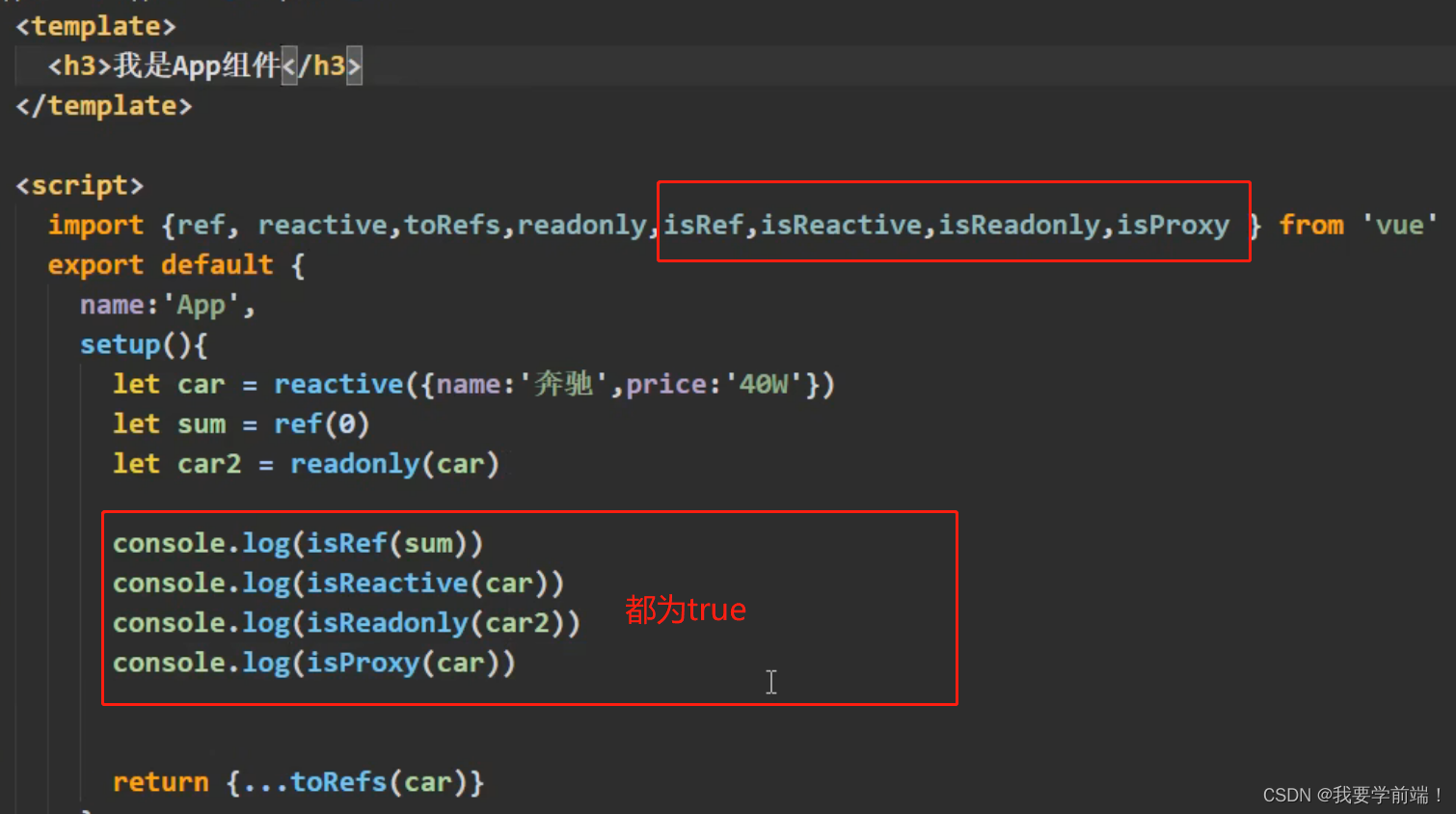
10_Vue3 其它的组合式API(Composition API)
Vue3 中的其它组合式API 1.shallowReactive 与 shallowRef 2. readonly 与 shallowReadonly 3.toRaw 与 markRaw 4.customRef 5.provide 与 inject 6.响应式数据的判断...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...
