Transformer 立体视觉 Depth Estimation
1. Intro
立体深度估计具有重要的意义,因为它能够重建三维信息。为此,在左右相机图像之间匹配相应的像素;对应像素位置的差异,即视差,可以用来推断深度并重建3D场景。最近基于深度学习的立体深度估计方法已经显示出有希望的结果,但仍然存在一些挑战。
其中一个挑战涉及使用有限的视差范围。理论上,视差值的范围可以从0到图像宽度,这取决于相机的分辨率/基线以及它们与物理对象的接近程度。然而,许多性能最好的方法都被限制在手动预先指定的视差范围内(通常最大值为192像素)[21]。这些方法依赖于“成本量”,其中计算多个候选匹配的匹配成本,并计算最终预测的差异值作为总和。这种自我施加的视差范围是必要的,以使这些方法的内存可行的实现,但不是灵活的物理场景和/或相机设置的属性。在自动驾驶和内窥镜干预等应用中,无论相机设置如何(视差值可能大于192),识别近距离物体以避免碰撞是很重要的,这表明需要放宽固定视差范围假设。
几何属性和约束,如遮挡和匹配唯一性,导致了非学习方法的成功,如[18],也经常在基于学习的方法中缺失。对于立体深度估计,遮挡区域没有有效的视差。先前的算法通常通过分段平滑假设来推断被遮挡区域的差异,这可能并不总是有效的。提供置信度估计和视差值将有利于下游分析,例如配准或场景理解算法,以便对遮挡和低置信度估计进行加权或拒绝。然而,大多数先前的方法不提供这样的信息。此外,一幅图像中的像素不应该与另一幅图像中的多个像素匹配(直到图像分辨率),因为它们对应于物理场景中的相同位置[28]。虽然这个约束对于解决歧义非常有用,但是大多数现有的基于学习的方法并没有强加它。
上述问题在很大程度上源于当代立体匹配观的缺陷,即试图构建一个成本体。从沿极线序列对序列匹配的角度考虑视差估计的方法可以避免这些挑战。这些方法并不新鲜
相关文章:

Transformer 立体视觉 Depth Estimation
1. Intro 立体深度估计具有重要的意义,因为它能够重建三维信息。为此,在左右相机图像之间匹配相应的像素;对应像素位置的差异,即视差,可以用来推断深度并重建3D场景。最近基于深度学习的立体深度估计方法已经显示出有希望的结果,但仍然存在一些挑战。 其中一个挑战涉及使…...
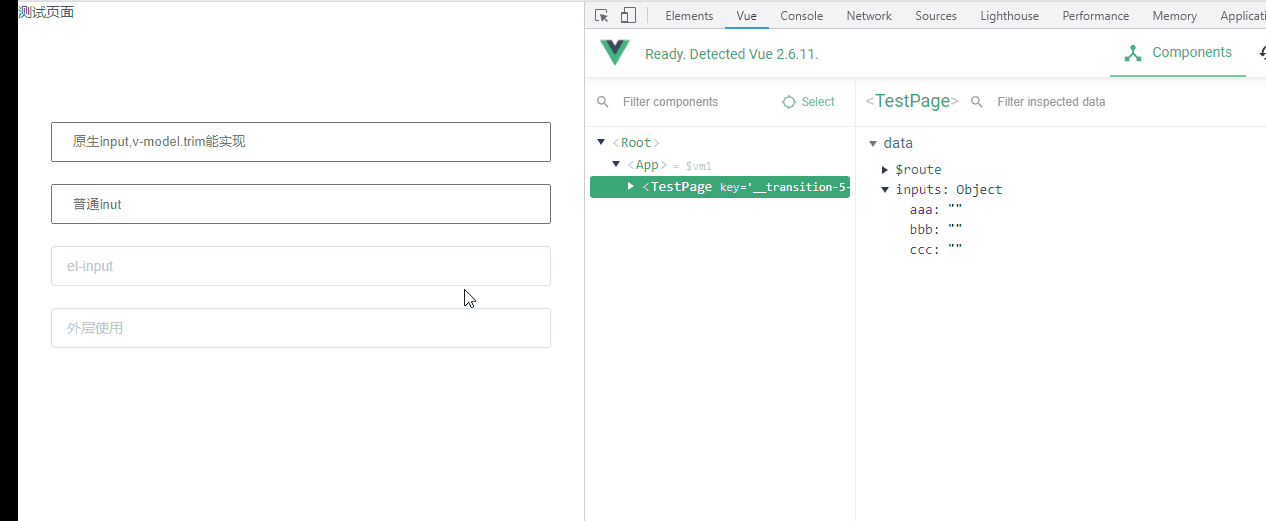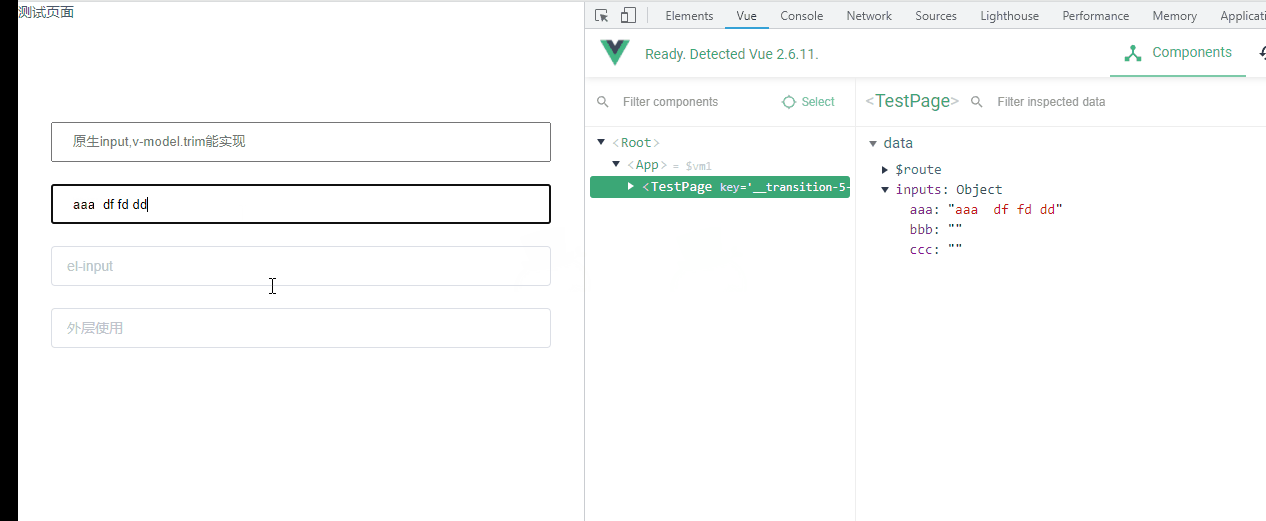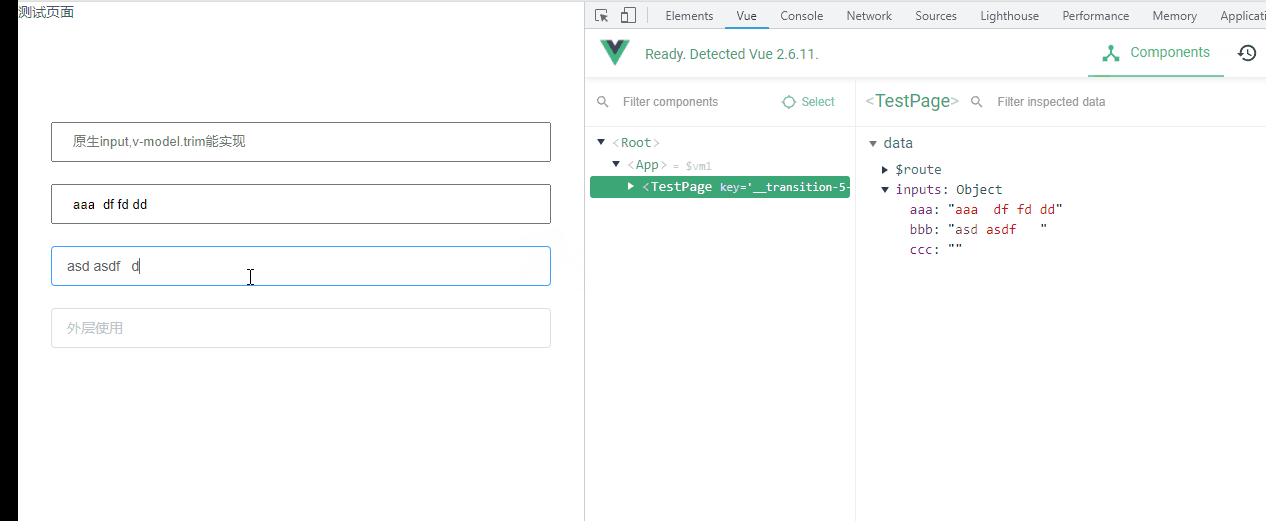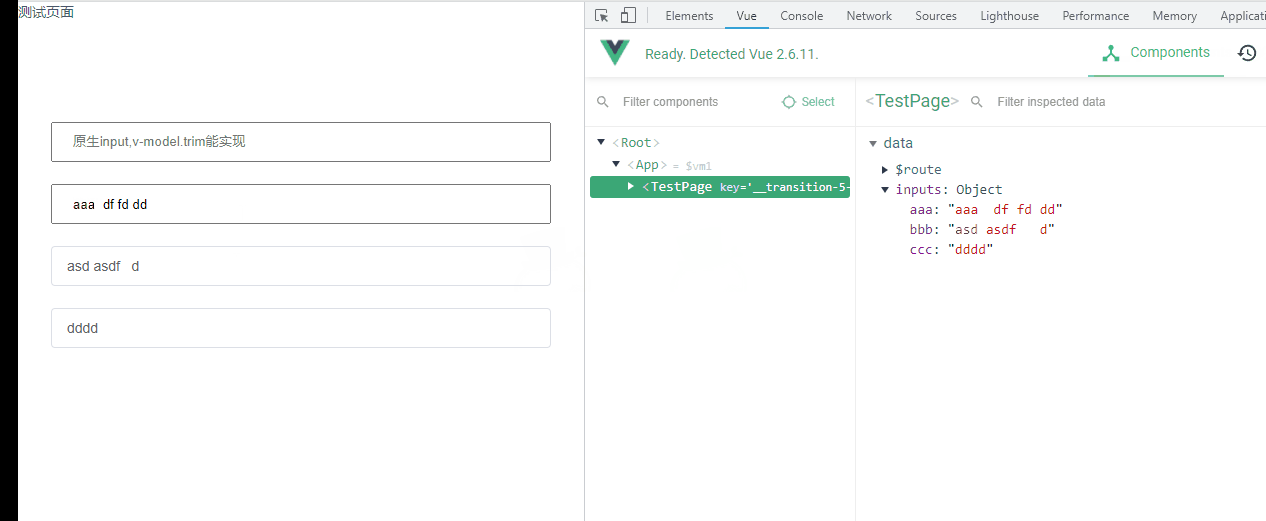
vue去掉所有输入框两边空格,封装指令去空格,支持Vue2和Vue3,ElementUI Input去空格
需求背景 就是页面很多表单输入框,期望在提交的时候,都要把用户两边的空格去掉 ❌使用 vue 的指令 .trim 去掉空格 中间会输入不了空格, 比如我想输入 你好啊 中国, 这中间的空格输入不了,只能变成 你好啊中国 ❌在提交的时候使用…...
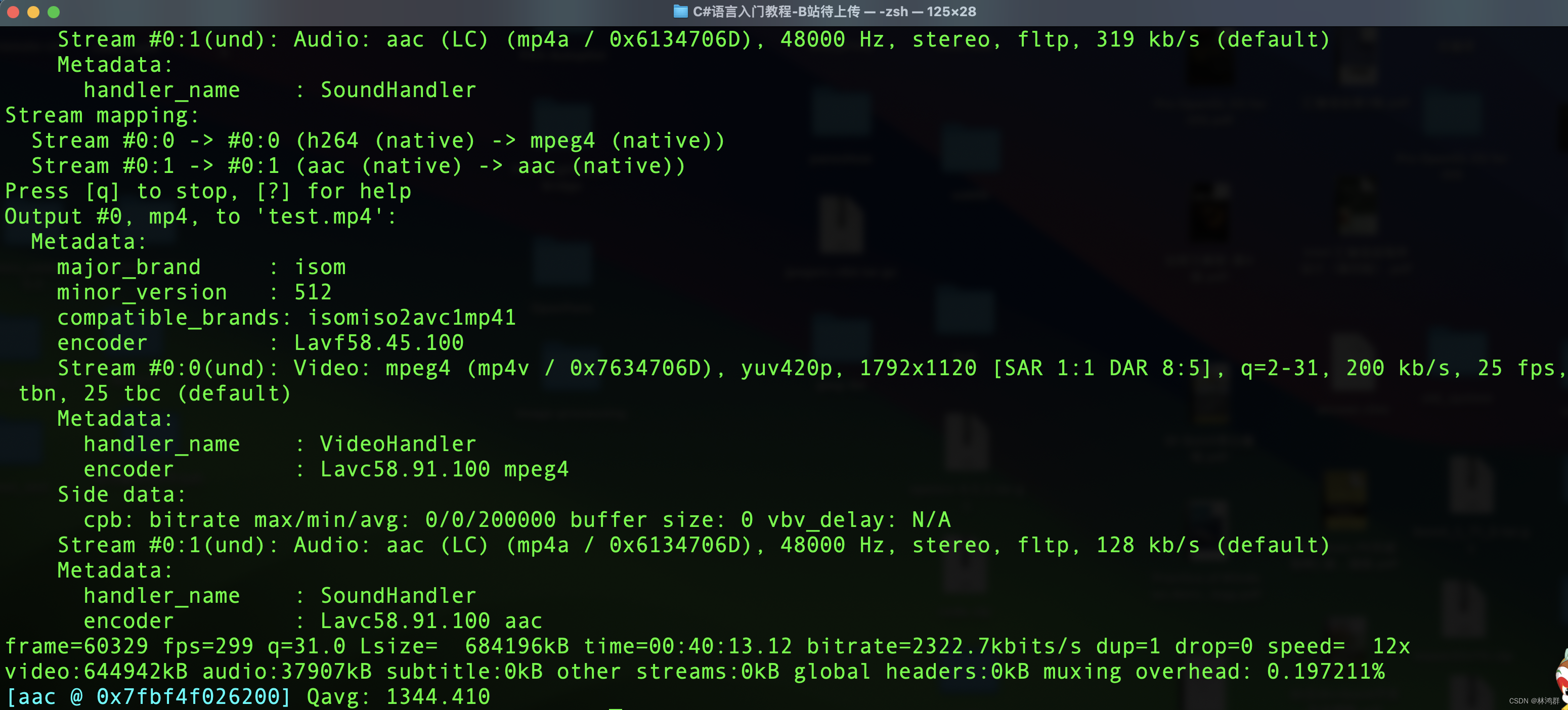
认识FFMPEG框架
FFMPEG全称: Fast Forward Moving Picture Experts Group (MPEG:动态图像专家组) ffmpeg相关网站: git://source.ffmpeg.org/ffmpeg.git http://git.videolan.org/?pffmpeg.git https://github.com/FFmpeg/FFmpeg FFMPEG框架基本组件: AVFormat , AVCodec, AVDevice, AVFil…...

Vue3 大屏数字滚动效果
父组件: <template> <div class"homePage"> <NumRoll v-for"(v, i) in numberList" :key"i" :number"v"></NumRoll> </div> </template> <script setup> import { onMounted, r…...
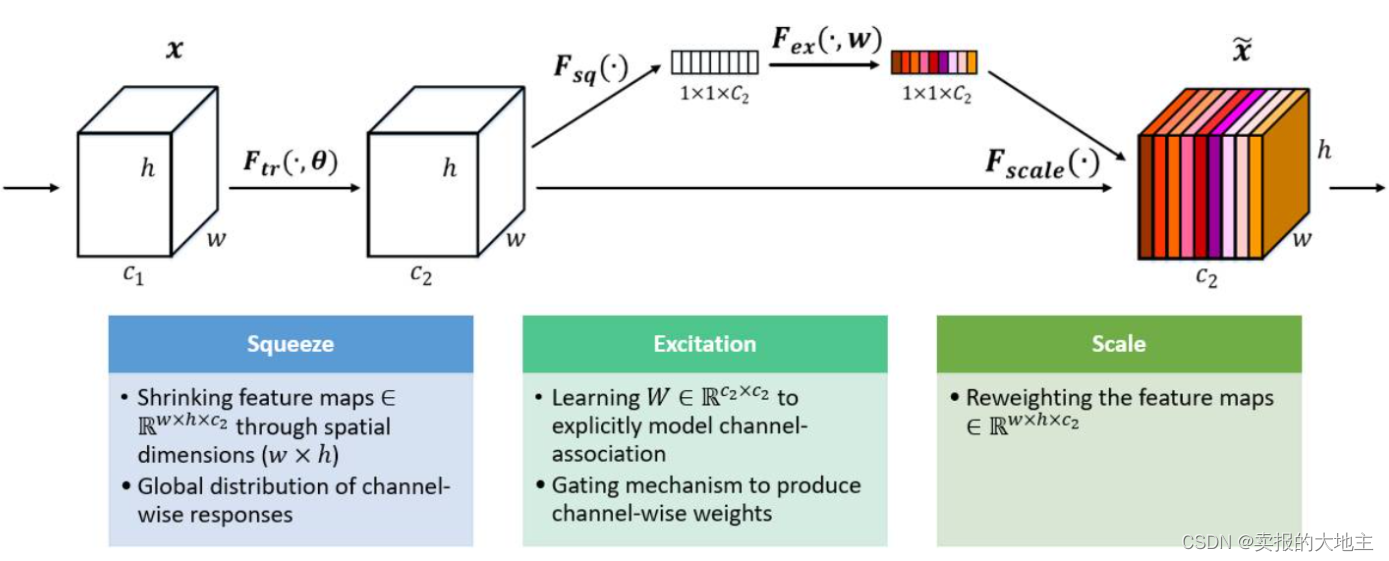
【深度学习注意力机制系列】—— SENet注意力机制(附pytorch实现)
深度学习中的注意力机制(Attention Mechanism)是一种模仿人类视觉和认知系统的方法,它允许神经网络在处理输入数据时集中注意力于相关的部分。通过引入注意力机制,神经网络能够自动地学习并选择性地关注输入中的重要信息ÿ…...

go 函数
go 语言函数 go 函数函数定义Go函数的特点如下函数作为参数可变参数相同类型可变参数不同类型可变参数 return语句作用概述空的return语句空白标识符多个返回值命名返回值 defer 语句作用引申出来的面试题for defer下面是一个使用defer的示例代码输出结果 匿名函数定义匿名函数…...

python之正则表达式
目录 正则表达式 python正则表达式方法 match search findall finditer compile 元字符匹配 元字符 量词 贪婪匹配和惰性匹配 正则表达式的group 语法 案例 正则表达式 正则表达式又称规则表达式,是使用单个字符串来描述、匹配某个句法规则的字符串…...
【LeetCode每日一题】——219.存在重复元素II
文章目录 一【题目类别】二【题目难度】三【题目编号】四【题目描述】五【题目示例】六【题目提示】七【解题思路】八【时间频度】九【代码实现】十【提交结果】 一【题目类别】 哈希表 二【题目难度】 简单 三【题目编号】 219.存在重复元素II 四【题目描述】 给你一个…...

篇六:适配器模式:让不兼容变兼容
篇六:“适配器模式:让不兼容变兼容” 开始本篇文章之前先推荐一个好用的学习工具,AIRIght,借助于AI助手工具,学习事半功倍。欢迎访问:http://airight.fun/ 另外有2本不错的关于设计模式的资料,…...

【云原生】Docker-compose中所有模块学习
compose模块 模板文件是使用 Compose 的核心,涉及到的指令关键字也比较多。但大家不用担心,这里面大部分指令跟 docker run 相关参数的含义都是类似的。 默认的模板文件名称为 docker-compose.yml,格式为 YAML 格式。 version: "3&quo…...

广义积分练习
前置知识 无穷限积分瑕积分 练习 计算 ∫ 0 ∞ 1 x ( 1 x ) d x \int_0^{\infty}\dfrac{1}{\sqrt x(1x)}dx ∫0∞x (1x)1dx 解: x 0 \qquad x0 x0为瑕点 \qquad 原式 lim a → 0 lim b → ∞ ∫ a b 1 x ( 1 x ) d x lim a → 0 lim …...
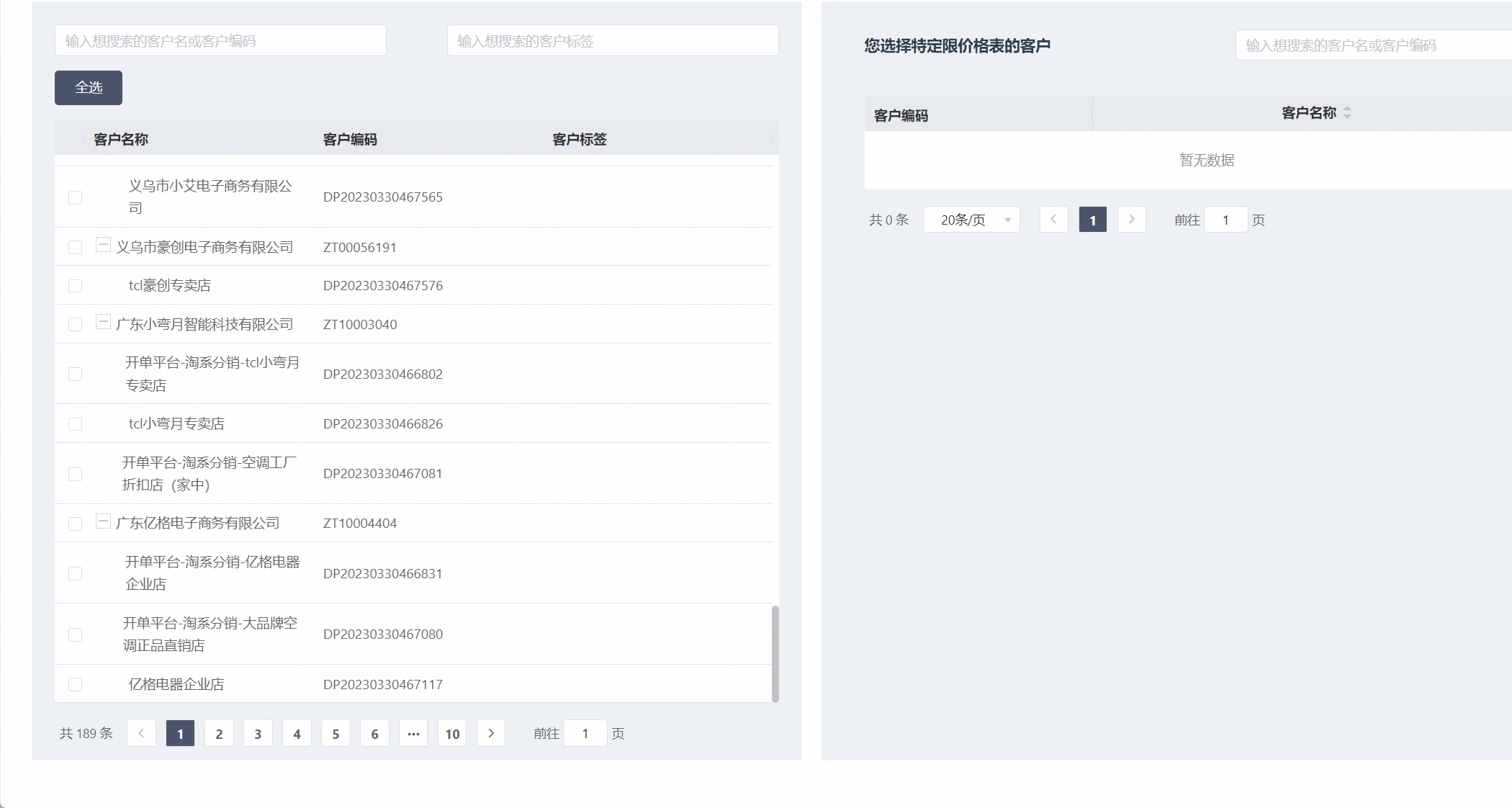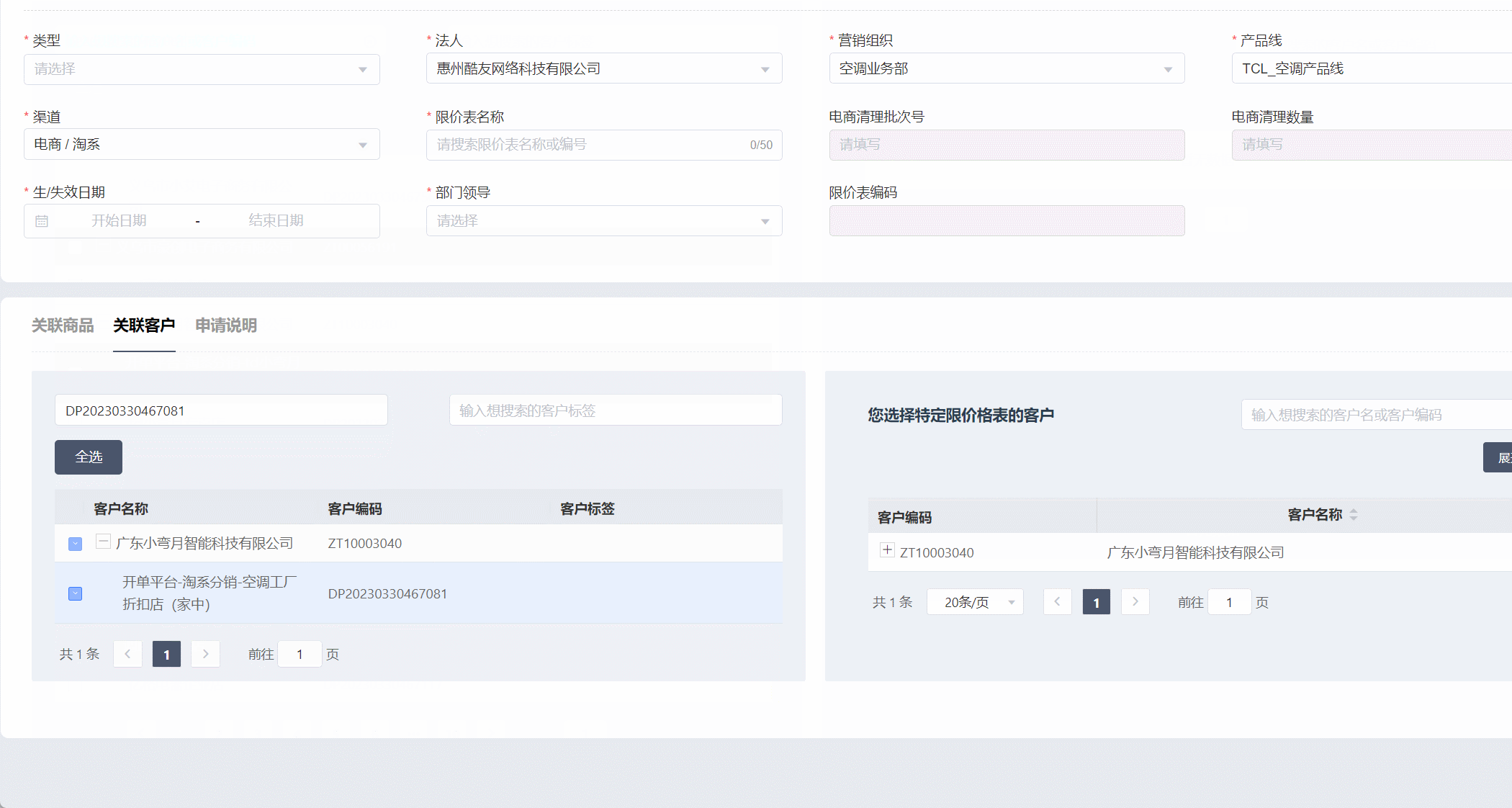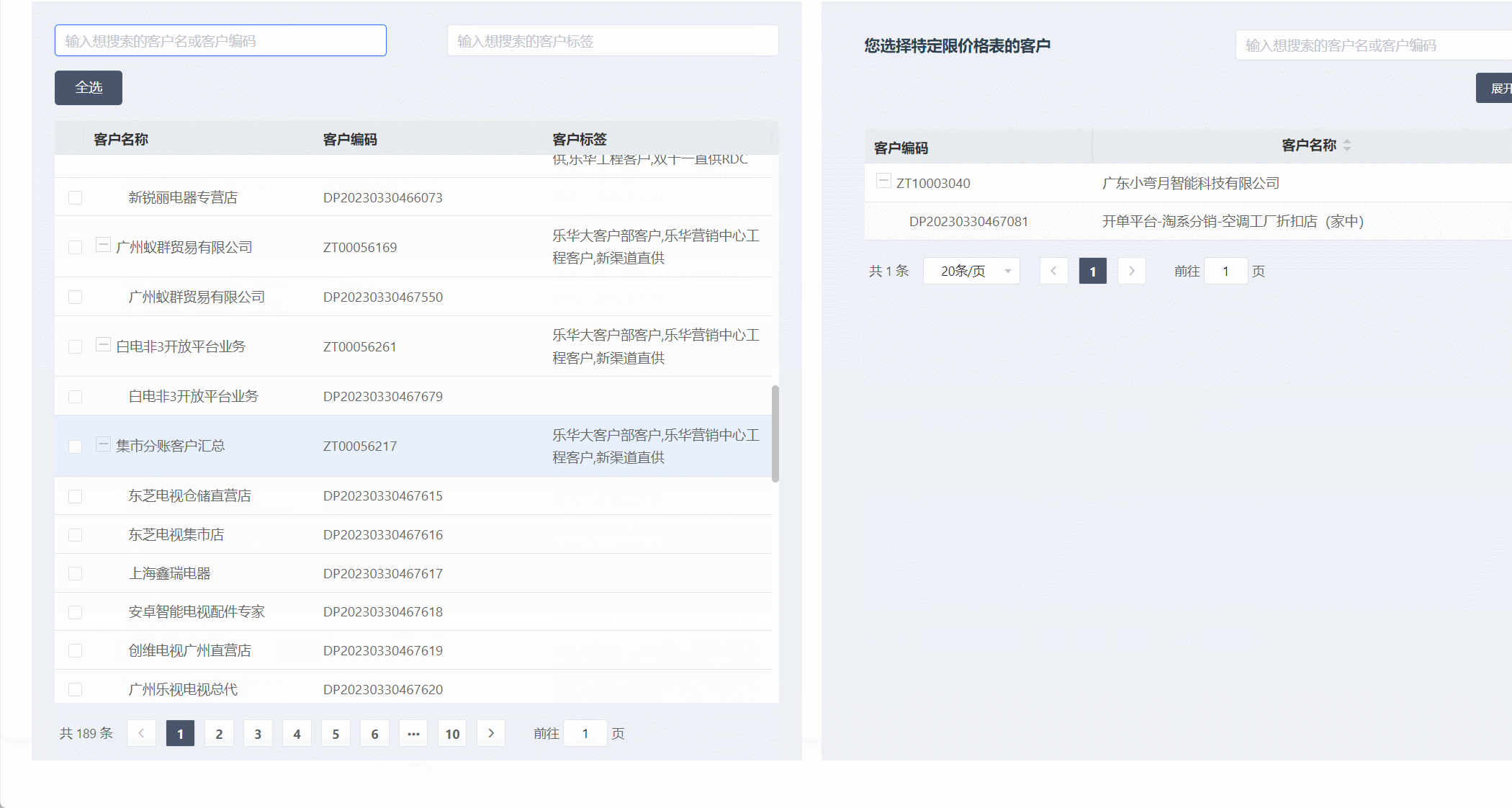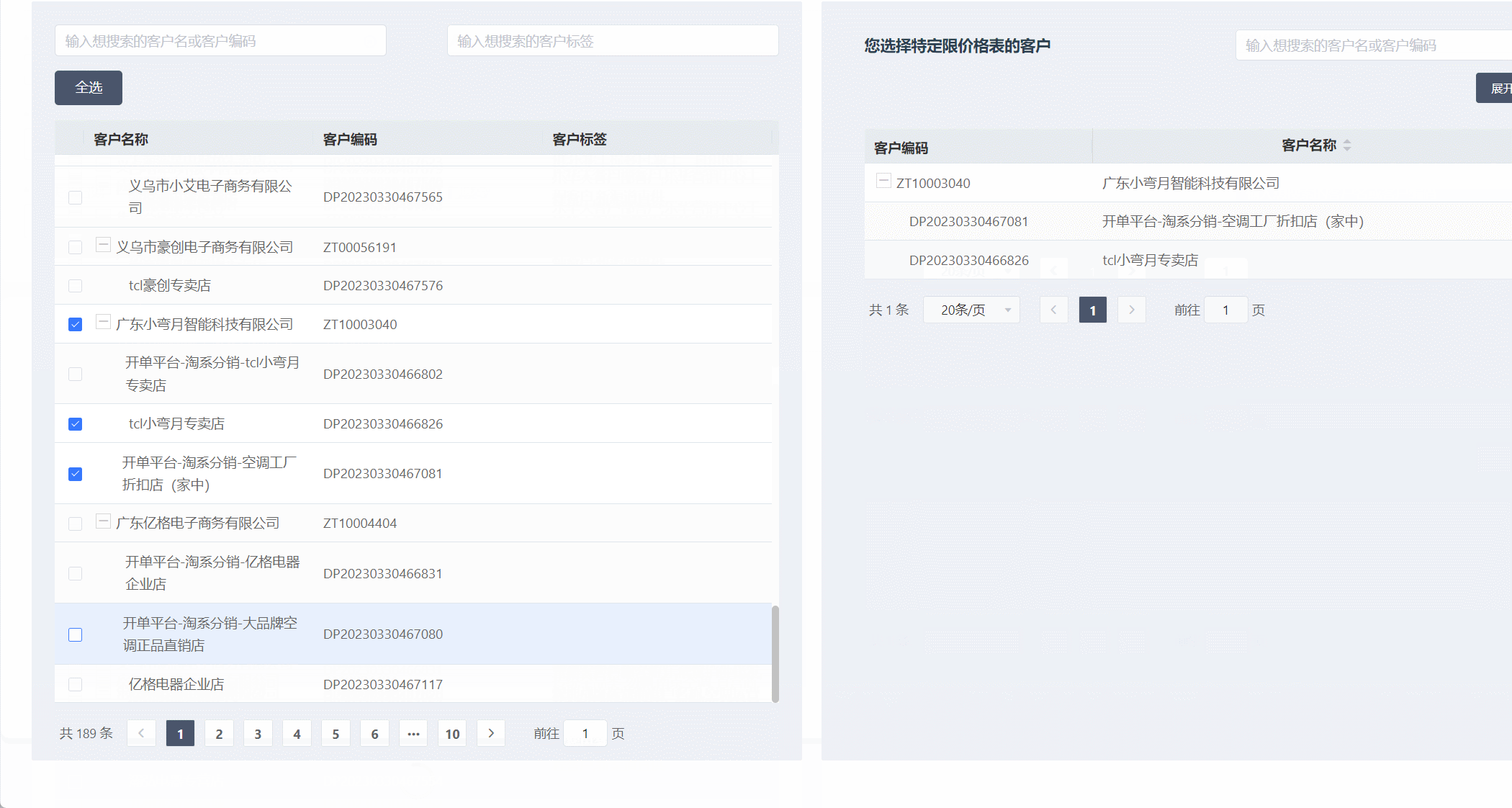
element-ui树形表格,左边勾选,右边显示选中的数据-功能(如动图)
功能如图 功能需求 表格树形表格勾选数据,右边显示对应勾选的数据内容,选中客户,自动勾选所有的店铺(子级),选中其中一个店铺,自动勾选上客户(父级),同时会存在只有客户(下面没有子级的情况&am…...

Android数字价格变化的动画效果的简单实现
原理:使用ValueAnimator属性动画类实现,它通过值的改变手动设置对象的属性值来实现动画效果。直接贴代码: public static void doNumberAnim(TextView tvPrice, float startNumber, float endNumber) {ValueAnimator animator ValueAnimato…...
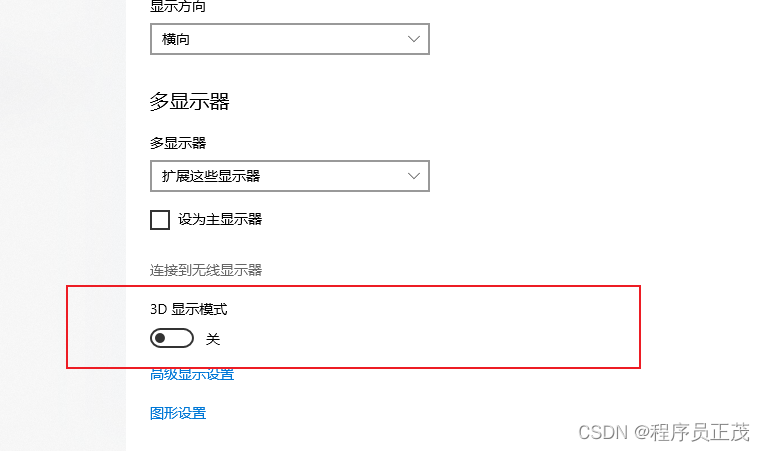
Win10无法投影关闭3D模式
Win10不小心开启了3D模式,插上投影仪就一闪一闪的,无法正投影 解决办法: 1. 打开注册表工具regedit,删除以下注册表,重启电脑 HKEY_LOCAL_MACHINE\SYSTEM\CurrentControlSet\Control\GraphicsDrivers\Configurat…...
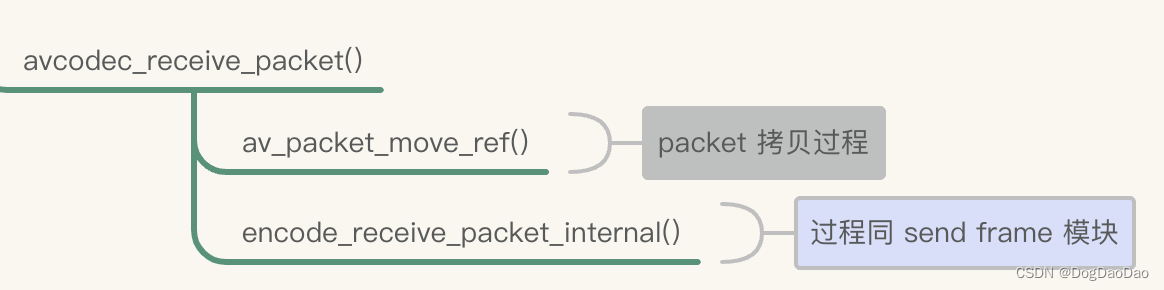
FFmpeg 编码详细流程
介绍 FFmpeg的 libavcodec 模块完成音视频多媒体的编解码模块。FFmpeg 本身不具有音视频编码的功能和底层能力,只是对各类第三方的编码器API 进行封装调用。老版本的 FFmpeg 将avcodec_encode_video2()作为视频的解码函数 API,将avcodec_encode_audio2(…...

05如何做微服务架构设计
一句话导读 微服务架构设计方法有:领域驱动设计DDD(Domain-Driven-Design)、12因素应用(12-Factor App)、事件驱动架构EDA(Event-Driven Architecture)等等,但是他们都必须遵守微服务…...
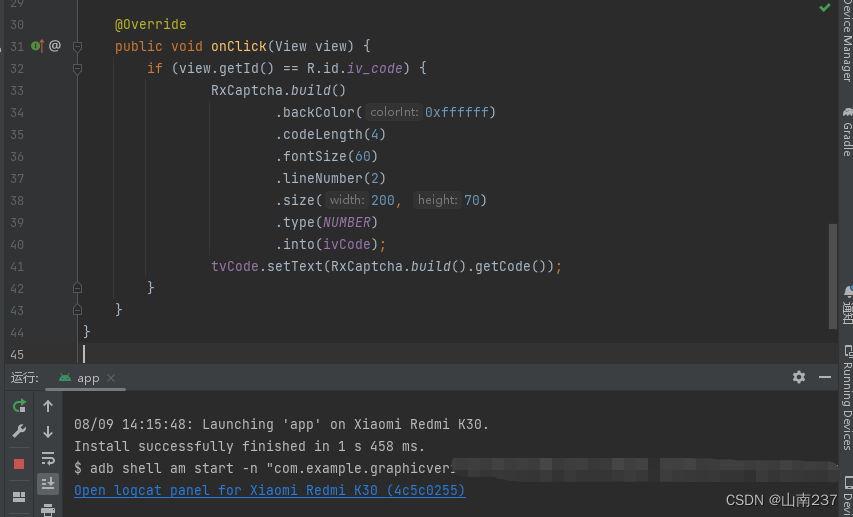
安卓开发问题记录:需要常量表达式
问题原因 写代码过程中爆出这个错误:需要常量表达式,定位到switch。 解决方法:把switch case,改成if else 错误源代码: public void onClick(View view) {switch (view.getId()) {case R.id.iv_code:RxCaptcha.build(…...

回归预测 | MATLAB实现基于SVM-RFE-BP支持向量机递归特征消除特征选择算法结合BP神经网络的多输入单输出回归预测
回归预测 | MATLAB实现基于SVM-RFE-BP支持向量机递归特征消除特征选择算法结合BP神经网络的多输入单输出回归预测 目录 回归预测 | MATLAB实现基于SVM-RFE-BP支持向量机递归特征消除特征选择算法结合BP神经网络的多输入单输出回归预测预测效果基本介绍研究内容程序设计参考资料…...

配置root账户ssh免密登录并使用docker-machine构建docker服务
简介 Docker Machine是一种可以在多种平台上快速安装和维护docker运行环境,并支持多种平台,让用户可以在很短时间内在本地或云环境中搭建一套docker主机集群的工具。 使用docker-machine命令,可以启动、审查、停止、重启托管的docker 也可以…...

【力扣周赛】第357场周赛
【力扣周赛】第357场周赛 2810. 故障键盘题目描述解题思路 2811. 判断是否能拆分数组题目描述解题思路 2810. 故障键盘 题目描述 描述:你的笔记本键盘存在故障,每当你在上面输入字符 ‘i’ 时,它会反转你所写的字符串。而输入其他字符则可以…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

pgsql:还原数据库后出现重复序列导致“more than one owned sequence found“报错问题的解决
问题: pgsql数据库通过备份数据库文件进行还原时,如果表中有自增序列,还原后可能会出现重复的序列,此时若向表中插入新行时会出现“more than one owned sequence found”的报错提示。 点击菜单“其它”-》“序列”,…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...

当下AI智能硬件方案浅谈
背景: 现在大模型出来以后,打破了常规的机械式的对话,人机对话变得更聪明一点。 对话用到的技术主要是实时音视频,简称为RTC。下游硬件厂商一般都不会去自己开发音视频技术,开发自己的大模型。商用方案多见为字节、百…...
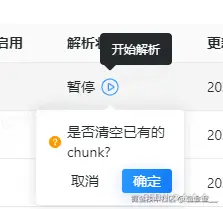
Element-Plus:popconfirm与tooltip一起使用不生效?
你们好,我是金金金。 场景 我正在使用Element-plus组件库当中的el-popconfirm和el-tooltip,产品要求是两个需要结合一起使用,也就是鼠标悬浮上去有提示文字,并且点击之后需要出现气泡确认框 代码 <el-popconfirm title"是…...
