idol!! 2023牛客暑期多校训练营6 C
登录—专业IT笔试面试备考平台_牛客网
题目大意:·定义n!!等于与n的奇偶性相同的所有小于等于n的数的阶乘之和,问n!!的末尾有多少0
1<=n<=1e18
思路:因为末尾0的来源是2*5,而2的个数明显比5的个数多得多,所以末尾0的个数就等于有多少个5相乘。
首先我们看所有奇数,在n的范围内有cnt1=(n+1)/2个奇数,然后我们观察发现,除了前两个奇数1,3之外,后面每5个数他们的因数中间包含的5的个数是相同的,比如5~13每个奇数都有一个因数5,15~23有两个,而25~33有4个35~43有5个,前两组和后两组5的个数都相差1,而两者之间相差2,这是因为25不仅有因数5,还有因数25额外提供了一个5,那么如果我们先不管额外提供的这个5,那么每一组5的个数都是等差数列,一共有cnt2=(cnt-1)/5组,每组大小s为5,那么总合也就是(1+cnt2)*s*cnt2/2。
然后所有数对应减去他们本次提供的贡献后,可以发现前两组数剩余5的个数都变成了0,下一组变成了25~73的个数为1,75~123的个数为2,125~173的个数为4,也就是新的等差数列的每组大小变成了a*5,其余都不变,所以我们可以从5开始枚举a,直到所有数的贡献都被计算完毕。
对于偶数,唯一的不同就是一开始前四个数的贡献为0,每次求等差数列后,前四组的贡献清零,分两次求奇偶再加起来就好
//#include<__msvc_all_public_headers.hpp>
#include<bits/stdc++.h>
using namespace std;
typedef __int128 ll;//答案超过了long long 的数据范围
ll read()
{//直接在函数里面实现读字符串操作更简洁ll res = 0;//初始结果赋值0char scan[1005];scanf("%s", scan);for (int i = 0; i < strlen(scan); i++)res *= 10, res += scan[i] - '0';//实现进位return res;//返回__int128类型
}
void print(ll num)
{//递归调用,实现从高位向低位输出if (num > 9)print(num / 10);putchar(num % 10 + '0');
}
int main()
{ll n = read();ll a = 1;ll ans = 0;ll cnt1 = (n + 1) / 2;//奇数的个数while (cnt1>0){a *= 5;//每组大小ll cnt2 = (cnt1 - 2) / a;//组数ll sum1 = (1 + cnt2) * a * cnt2 / 2;//求等差数列和ll mod = (cnt1 - 2) % a;//不在组里的余数sum1 += (cnt2 + 1) * mod;//单独算一下余数ans += sum1;cnt1 -= 2 * a;//维护剩余有攻陷的数的个数}if (ans < 0){//特判cnt=1print(0);return 0;}a = 1;cnt1 = n / 2;//偶数的的个数while (cnt1>0){a *= 5;ll cnt2 = (cnt1 - 4) / a;//前四组贡献为0ll sum1 = (1 + cnt2) * a * cnt2 / 2;ll mod = (cnt1 - 4) % a;sum1 += (cnt2 + 1) * mod;ans += sum1;cnt1 -= 4 * a;}if (ans < 0){//特判cnt1=1,2,3print(0);return 0;}print(ans);return 0;
}
相关文章:

idol!! 2023牛客暑期多校训练营6 C
登录—专业IT笔试面试备考平台_牛客网 题目大意:定义n!!等于与n的奇偶性相同的所有小于等于n的数的阶乘之和,问n!!的末尾有多少0 1<n<1e18 思路:因为末尾0的来源是2*5,而2的个数明显比5的个数多得多,所以末尾…...
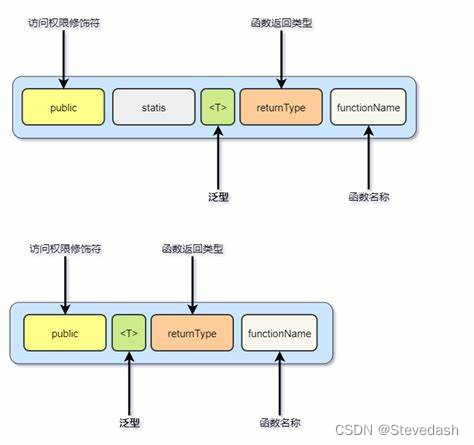
深入理解Jdk5引入的Java泛型:类型安全与灵活性并存
深入理解Jdk5引入的Java泛型:类型安全与灵活性并存 在Java的中,有一个强大的工具,它可以让你在编写代码时既保持类型安全,又享受灵活性。**这个工具就是——泛型(Generics)。**本文将引导你深入了解Java…...
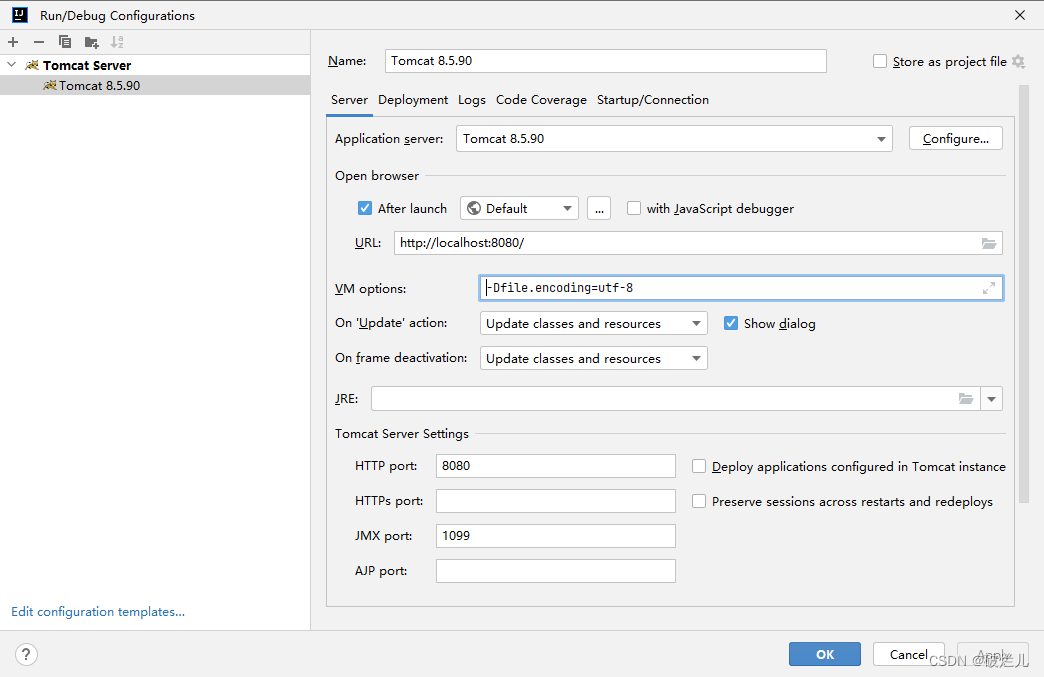
idea在控制台中输出文字显示乱码
VM options中加入下面这行 -Dfile.encodingutf-8...
hacksudo3 通关详解
环境配置 一开始桥接错网卡了 搞了半天 改回来就行了 信息收集 漏洞发现 扫个目录 大概看了一眼没什么有用的信息 然后对着login.php跑了一下弱口令 sqlmap 都没跑出来 那么利用点应该不在这 考虑到之前有过dirsearch字典太小扫不到东西的经历 换个gobuster扫一下 先看看g…...
)
CentOS 虚拟机磁盘扩容(非常实用)
新手村的选手在刚开始安装使用 CentOS 虚拟机时,很多选项都会按照推荐操作来,比如:磁盘推荐大小为 20 GB;但随着后面的使用,总会因为“磁盘根目录不足”原因,而导致软件无法安装、虚拟机无法正常运行等&…...
docker案例复现
$uri导致的CRLF注入漏洞 前期准备dockerdocker compose 漏洞配置 前期准备 docker 要完成这样的测试,需要我们有一定的环境,也就是需要大家去安装docker 更新系统软件包: sudo yum update 安装 Docker 的依赖软件包: sudo yum …...

淘宝资源采集(从零开始学习淘宝数据爬取)
1. 为什么要进行淘宝数据爬取? 淘宝数据爬取是指通过自动化程序从淘宝网站上获取数据的过程。这些数据可以包括商品信息、销售数据、评论等等。淘宝数据爬取可以帮助您了解市场趋势、优化您的产品选择以及提高销售额。 淘宝作为全球的电商平台,每天都有…...
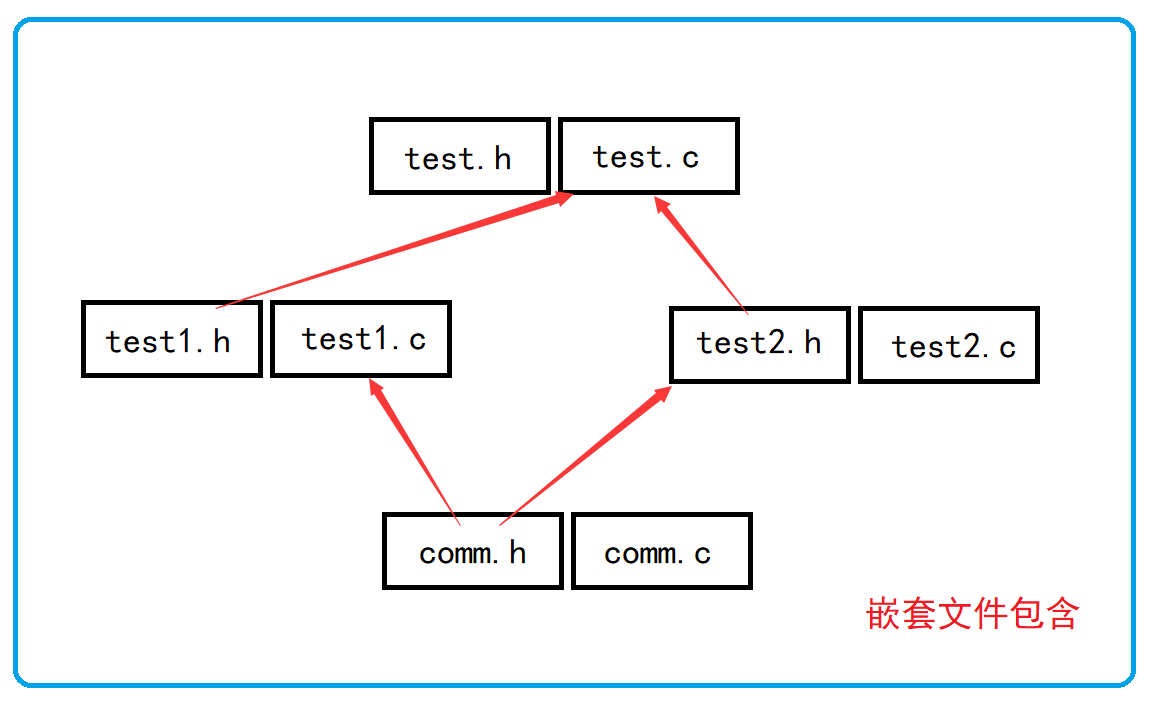
【C语言】预处理详解
本文目录 1 预定义符号 2 #define 2.1 #define 定义标识符 2.2 #define 定义宏 2.3 #define 替换规则 2.4 #和## 2.5 带副作用的宏参数 2.6 宏和函数对比 2.7 命名约定 3 #undef 4 命令行定义 5 条件编译 6 文件包含 6.1 头文件被包含的方式 6.2 嵌套文件包含 1 预定义符号 __…...

2023中国(合肥)场景创新峰会成功举办,全息网御被纳入《合肥市第二批场景能力清单》
场景作为重要的城市资源,在驱动科技创新、产业发展、城市治理方面发挥着重要作用。近年来,为促进数字技术与实体经济深度融合,加速前沿科技转化落地、吸引全球创新资源集聚,合肥市聚焦“双找”:为产品找场景࿰…...
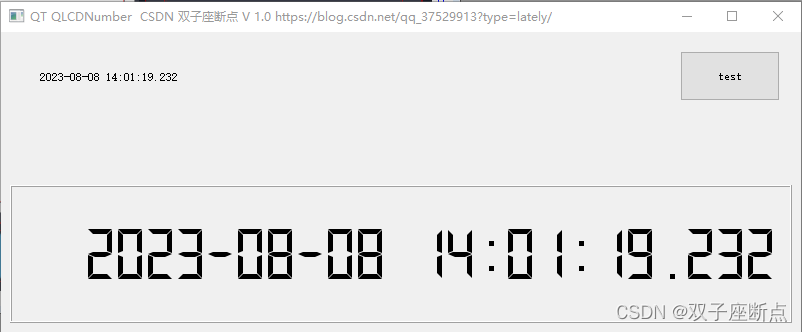
QT QLCDNumber 使用详解
本文详细的介绍了QLCDNumber控件的各种操作,例如:新建界面、源文件、设置显示位数、设置进制、设置外观、设置小数点、设置溢出、显示事件、其它文章等等操作。 实际开发中,一个界面上可能包含十几个控件,手动调整它们的位置既费时…...
明年,HarmonyOS不再兼容Android应用!
2023年华为开发者大会,不知道各位老铁们是否观看了,一个震撼的消息就是,首次公开了HarmonyOS NEXT的概念,简而言之就是,这是一款专为开发者打造的预览版操作系统,旨在提供"纯正鸿蒙操作系统"的体…...
)
华为OD机试 - 人气最高的店铺(Java JS Python)
题目描述 某购物城有m个商铺,现决定举办一场活动选出人气最高店铺。 活动共有n位市民参与,每位市民只能投一票,但1号店铺如果给该市民发放 q 元的购物补贴,该市民会改为投1号店铺。 请计算1号店铺需要最少发放多少元购物补贴才能成为人气最高店铺(即获得的票数要大于其…...

mysql sql 语句sum求和嵌套数学表达式
今天有个需求, 已减高度 高度 x 单双开(单开1 双开2) x 2,要直接写在sql语句中。 表字段 包含 高度 和 单双开字段 值是字符串 (双开 左单开 右单开) -- 已减高度 2 * 单双开 * 高度 sum( -- 求和 表达式 已减高度 2 * 单双开 * 高度 t_cloth.hegiht * 2 * (case WHEN l…...
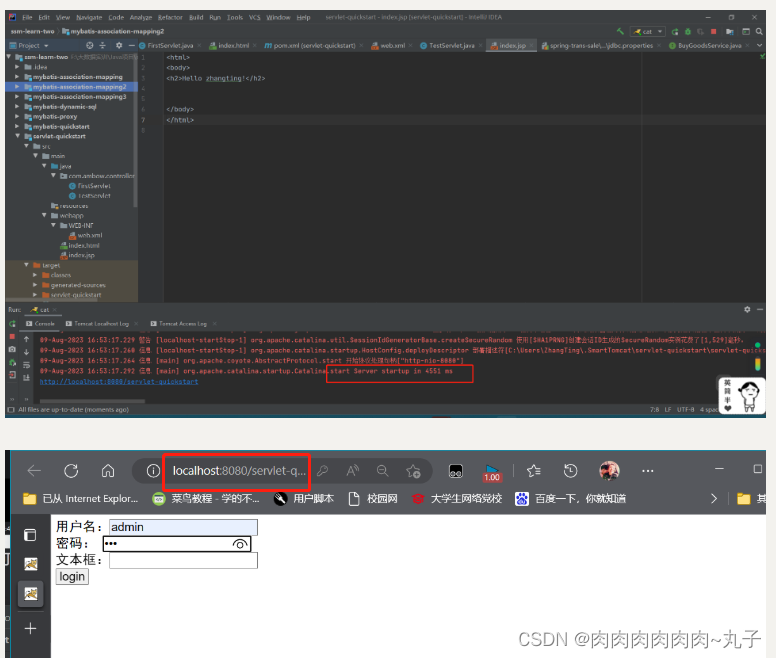
Java课题笔记~ Servlet编程
1.Servlet编程基础 (1)什么是Servlet Servlet是基于Java语言的Web编程技术,部署在服务器端的Web容器里,获取客户端的访问请求,并根据请求生成响应信息返回给客户端。 创建Servlet的方式,有 如下图:一般创建Servlet都…...

修改IDEA的idea.vmoptions参数导致IDEA无法打开(ReservedCodeCacheSize)
事发原因 Maven导依赖的时候OOM,因此怀疑是内存太小,尝试修改idea.vmoptions的参数,然后发现IDEA重启后打不开了,卸载重装后也无法打开。。。 实际上如果导包爆出OOM的话应该调整下图参数,不过这都是后话了 解决思路…...

P1321 单词覆盖还原
题目描述 一个长度为 l l l 的字符串中被反复贴有 boy 和 girl 两单词,后贴上的可能覆盖已贴上的单词(没有被覆盖的用句点表示),最终每个单词至少有一个字符没有被覆盖。问贴有几个 boy 几个 girl? 输入格式 一行被…...
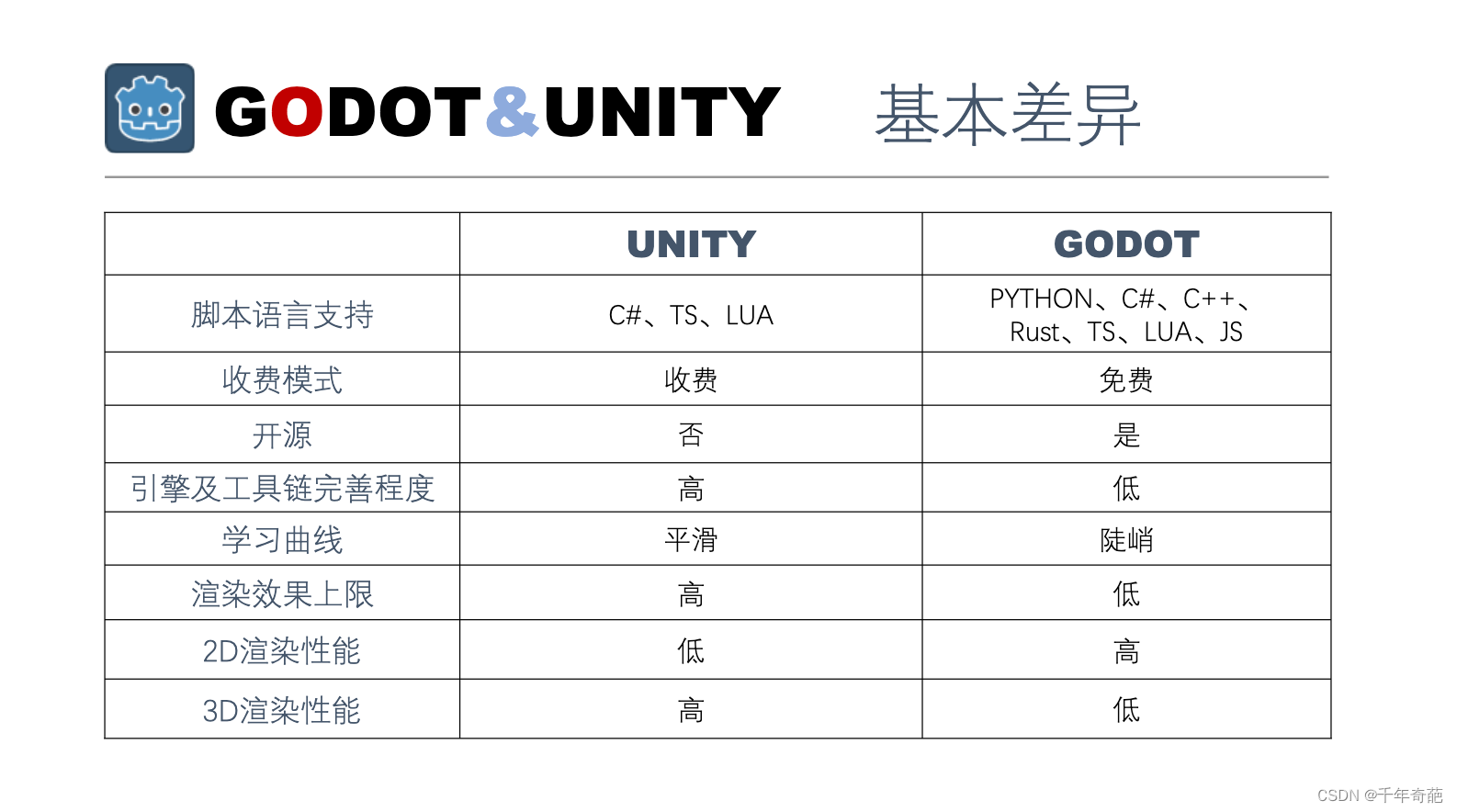
GODOT游戏引擎简介,包含与unity性能对比测试,以及选型建议
GODOT,是一个免费开源的3D引擎。本文以unity作对比,简述两者区别和选型建议。由于是很久以前写的ppt,技术原因视频和部分章节丢失了。建议当做业务参考。 GODOT目前为止遇到3个比较重大的基于,第一个是oprea的合作奖,…...
Add-in Express for Microsoft Office and Delphi Crack
Add-in Express for Microsoft Office and Delphi Crack 适用于Microsoft Office和Delphi VCL的Add-in Express使您能够在几次点击中为Microsoft Office开发专业插件。它生成基于COM的项目,这些项目包含Microsoft Office外接程序或智能标记的所有必要功能࿰…...

opencv基础-34 图像平滑处理-2D 卷积 cv2.filter2D()
2D卷积是一种图像处理和计算机视觉中常用的操作,用于在图像上应用滤波器或卷积核,从而对图像进行特征提取、平滑处理或边缘检测等操作。 在2D卷积中,图像和卷积核都是二维的矩阵或数组。卷积操作将卷积核在图像上滑动,对每个局部区…...

webSocket 与传统的 http 有什么优势
webSocket 与传统的 http 有什么优势 当页面中需要观察实时数据的变化(比如聊天、k 线图)时,过去我们往往使用两种方式完成 第一种是短轮询,即客户端每隔一段时间就向服务器发送消息,询问有没有新的数据 第二种是长轮询…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...
