【vue3】基础知识点-setup语法糖
学习vue3,都会从基础知识点学起。了解setup函数,ref,recative,watch、comptued、pinia等如何使用
今天说vue3组合式api,setup函数
在学习过程中一开始接触到的是这样的,定义数据且都要通过return返回
<script>
export default {
setup(){
cosnt message = 'new day
const logMessage= ()=>{
console.log(message)
}
return {
message,
logMessage
}
}
}
</script>
最新接触到的是这样的
<script setup>
cosnt message = 'new day
const logMessage= ()=>{
console.log(message)
}
</script>
两种不同的写法,那区别是什么呢?
其实在script标签上直接加setup就是语法糖写法
语法糖写法,简单理解就是经过一定的封装,将之前复杂的写法变成一个简单的写法
原先的export default 、setup(){} ,return 都不需要写了
官方提供了一个工具,可以在线看实际运行后的代码
戳这里,跳转到vue SFC Playground官方工具
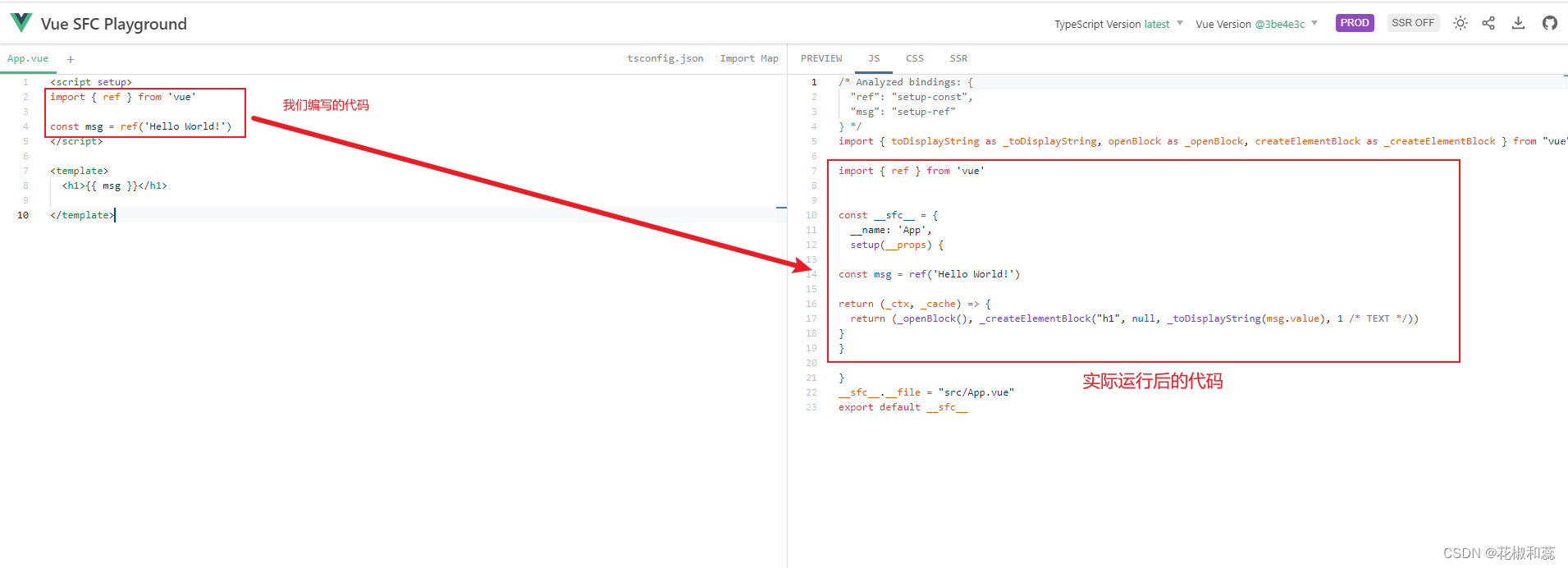
看右侧实际运行的代码,是同之前的复杂写法的。在底层运行的时候还是一开始的复杂写法,只是通过封装,提供给我们一个简单的写法,这就是语法糖的意义。
相关文章:

【vue3】基础知识点-setup语法糖
学习vue3,都会从基础知识点学起。了解setup函数,ref,recative,watch、comptued、pinia等如何使用 今天说vue3组合式api,setup函数 在学习过程中一开始接触到的是这样的,定义数据且都要通过return返回 <…...

idol!! 2023牛客暑期多校训练营6 C
登录—专业IT笔试面试备考平台_牛客网 题目大意:定义n!!等于与n的奇偶性相同的所有小于等于n的数的阶乘之和,问n!!的末尾有多少0 1<n<1e18 思路:因为末尾0的来源是2*5,而2的个数明显比5的个数多得多,所以末尾…...
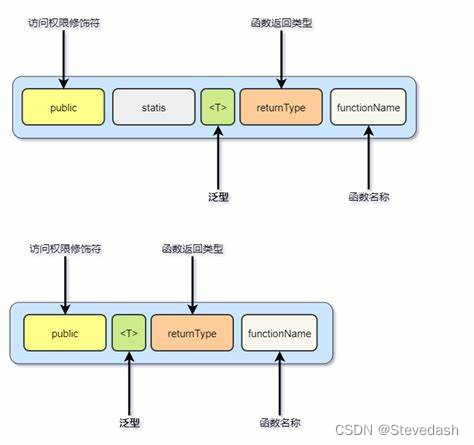
深入理解Jdk5引入的Java泛型:类型安全与灵活性并存
深入理解Jdk5引入的Java泛型:类型安全与灵活性并存 在Java的中,有一个强大的工具,它可以让你在编写代码时既保持类型安全,又享受灵活性。**这个工具就是——泛型(Generics)。**本文将引导你深入了解Java…...
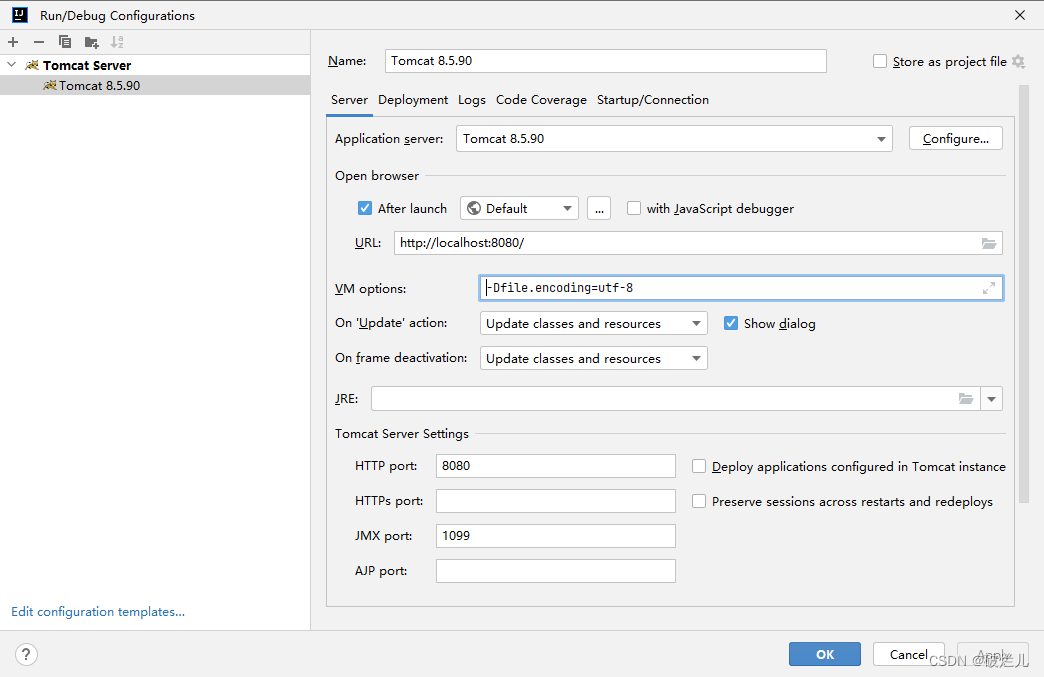
idea在控制台中输出文字显示乱码
VM options中加入下面这行 -Dfile.encodingutf-8...
hacksudo3 通关详解
环境配置 一开始桥接错网卡了 搞了半天 改回来就行了 信息收集 漏洞发现 扫个目录 大概看了一眼没什么有用的信息 然后对着login.php跑了一下弱口令 sqlmap 都没跑出来 那么利用点应该不在这 考虑到之前有过dirsearch字典太小扫不到东西的经历 换个gobuster扫一下 先看看g…...
)
CentOS 虚拟机磁盘扩容(非常实用)
新手村的选手在刚开始安装使用 CentOS 虚拟机时,很多选项都会按照推荐操作来,比如:磁盘推荐大小为 20 GB;但随着后面的使用,总会因为“磁盘根目录不足”原因,而导致软件无法安装、虚拟机无法正常运行等&…...
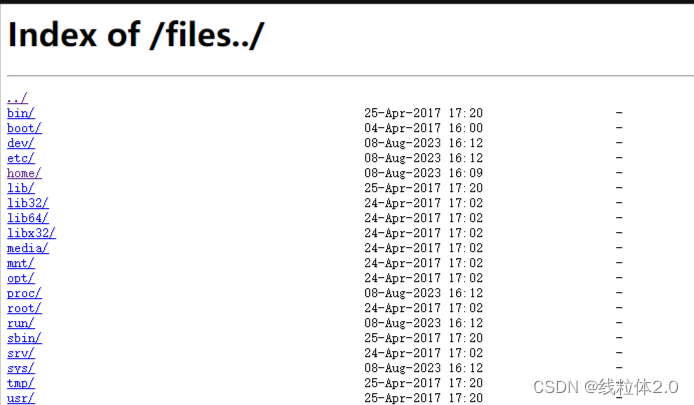
docker案例复现
$uri导致的CRLF注入漏洞 前期准备dockerdocker compose 漏洞配置 前期准备 docker 要完成这样的测试,需要我们有一定的环境,也就是需要大家去安装docker 更新系统软件包: sudo yum update 安装 Docker 的依赖软件包: sudo yum …...

淘宝资源采集(从零开始学习淘宝数据爬取)
1. 为什么要进行淘宝数据爬取? 淘宝数据爬取是指通过自动化程序从淘宝网站上获取数据的过程。这些数据可以包括商品信息、销售数据、评论等等。淘宝数据爬取可以帮助您了解市场趋势、优化您的产品选择以及提高销售额。 淘宝作为全球的电商平台,每天都有…...
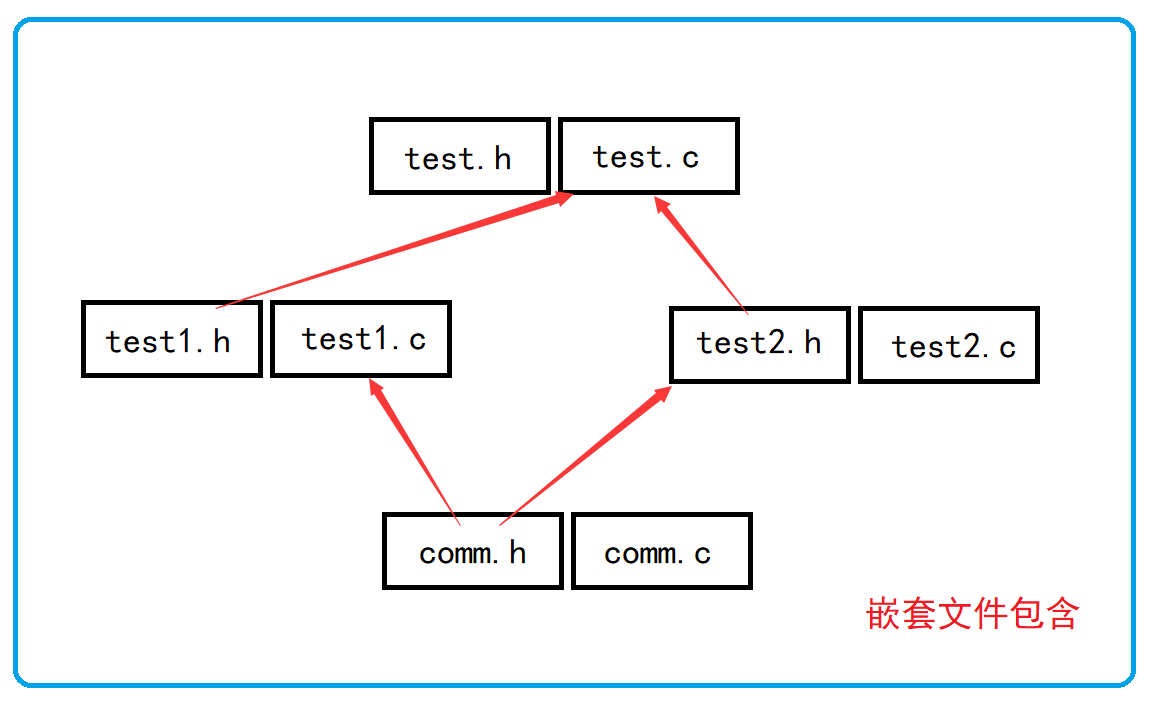
【C语言】预处理详解
本文目录 1 预定义符号 2 #define 2.1 #define 定义标识符 2.2 #define 定义宏 2.3 #define 替换规则 2.4 #和## 2.5 带副作用的宏参数 2.6 宏和函数对比 2.7 命名约定 3 #undef 4 命令行定义 5 条件编译 6 文件包含 6.1 头文件被包含的方式 6.2 嵌套文件包含 1 预定义符号 __…...

2023中国(合肥)场景创新峰会成功举办,全息网御被纳入《合肥市第二批场景能力清单》
场景作为重要的城市资源,在驱动科技创新、产业发展、城市治理方面发挥着重要作用。近年来,为促进数字技术与实体经济深度融合,加速前沿科技转化落地、吸引全球创新资源集聚,合肥市聚焦“双找”:为产品找场景࿰…...
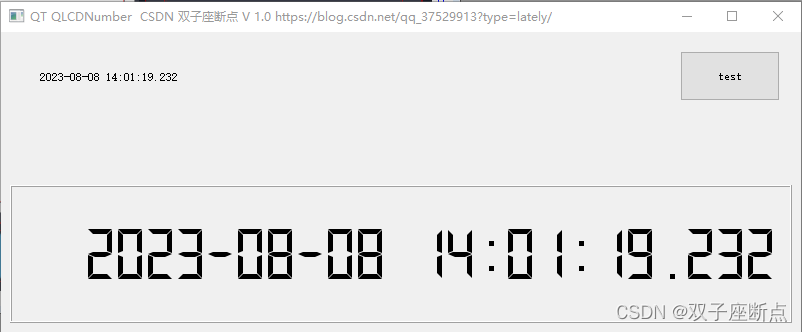
QT QLCDNumber 使用详解
本文详细的介绍了QLCDNumber控件的各种操作,例如:新建界面、源文件、设置显示位数、设置进制、设置外观、设置小数点、设置溢出、显示事件、其它文章等等操作。 实际开发中,一个界面上可能包含十几个控件,手动调整它们的位置既费时…...
明年,HarmonyOS不再兼容Android应用!
2023年华为开发者大会,不知道各位老铁们是否观看了,一个震撼的消息就是,首次公开了HarmonyOS NEXT的概念,简而言之就是,这是一款专为开发者打造的预览版操作系统,旨在提供"纯正鸿蒙操作系统"的体…...
)
华为OD机试 - 人气最高的店铺(Java JS Python)
题目描述 某购物城有m个商铺,现决定举办一场活动选出人气最高店铺。 活动共有n位市民参与,每位市民只能投一票,但1号店铺如果给该市民发放 q 元的购物补贴,该市民会改为投1号店铺。 请计算1号店铺需要最少发放多少元购物补贴才能成为人气最高店铺(即获得的票数要大于其…...

mysql sql 语句sum求和嵌套数学表达式
今天有个需求, 已减高度 高度 x 单双开(单开1 双开2) x 2,要直接写在sql语句中。 表字段 包含 高度 和 单双开字段 值是字符串 (双开 左单开 右单开) -- 已减高度 2 * 单双开 * 高度 sum( -- 求和 表达式 已减高度 2 * 单双开 * 高度 t_cloth.hegiht * 2 * (case WHEN l…...
Java课题笔记~ Servlet编程
1.Servlet编程基础 (1)什么是Servlet Servlet是基于Java语言的Web编程技术,部署在服务器端的Web容器里,获取客户端的访问请求,并根据请求生成响应信息返回给客户端。 创建Servlet的方式,有 如下图:一般创建Servlet都…...

修改IDEA的idea.vmoptions参数导致IDEA无法打开(ReservedCodeCacheSize)
事发原因 Maven导依赖的时候OOM,因此怀疑是内存太小,尝试修改idea.vmoptions的参数,然后发现IDEA重启后打不开了,卸载重装后也无法打开。。。 实际上如果导包爆出OOM的话应该调整下图参数,不过这都是后话了 解决思路…...

P1321 单词覆盖还原
题目描述 一个长度为 l l l 的字符串中被反复贴有 boy 和 girl 两单词,后贴上的可能覆盖已贴上的单词(没有被覆盖的用句点表示),最终每个单词至少有一个字符没有被覆盖。问贴有几个 boy 几个 girl? 输入格式 一行被…...
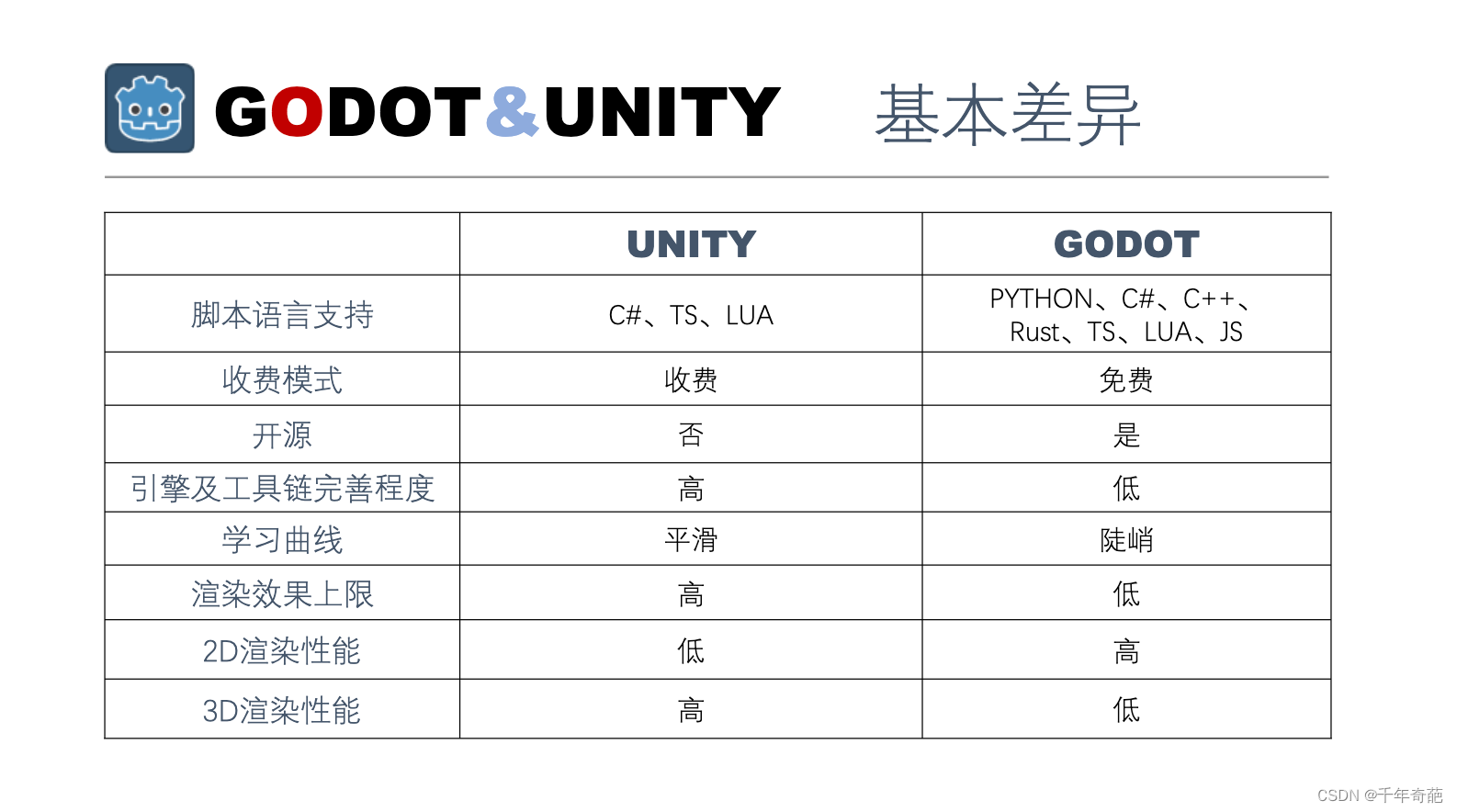
GODOT游戏引擎简介,包含与unity性能对比测试,以及选型建议
GODOT,是一个免费开源的3D引擎。本文以unity作对比,简述两者区别和选型建议。由于是很久以前写的ppt,技术原因视频和部分章节丢失了。建议当做业务参考。 GODOT目前为止遇到3个比较重大的基于,第一个是oprea的合作奖,…...
Add-in Express for Microsoft Office and Delphi Crack
Add-in Express for Microsoft Office and Delphi Crack 适用于Microsoft Office和Delphi VCL的Add-in Express使您能够在几次点击中为Microsoft Office开发专业插件。它生成基于COM的项目,这些项目包含Microsoft Office外接程序或智能标记的所有必要功能࿰…...

opencv基础-34 图像平滑处理-2D 卷积 cv2.filter2D()
2D卷积是一种图像处理和计算机视觉中常用的操作,用于在图像上应用滤波器或卷积核,从而对图像进行特征提取、平滑处理或边缘检测等操作。 在2D卷积中,图像和卷积核都是二维的矩阵或数组。卷积操作将卷积核在图像上滑动,对每个局部区…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...
