三大基础排序算法——冒泡排序、选择排序、插入排序
目录
- 前言
- 一、排序简介
- 二、冒泡排序
- 三、选择排序
- 四、插入排序
- 五、对比
- References
前言
在此之前,我们已经介绍了十大排序算法中的:归并排序、快速排序、堆排序(还不知道的小伙伴们可以参考我的 「数据结构与算法」 专栏),今天我们就来介绍三大基础的排序算法:冒泡排序,选择排序和插入排序。
一、排序简介
排序算法(Sorting Algorithm)是一种将一组特定的数据按某种顺序进行排列的算法。排序算法多种多样,性质也大多不同。
稳定性
排序算法的稳定性并不是指最坏时间复杂度和最好时间复杂度是否相等,而是指相等的元素在经过排序之后其相对位置是否发生改变。
下图展示了稳定排序和不稳定排序之间的区别:

按照是否稳定可对十大排序算法做出如下分类:
| 稳定排序 | 不稳定排序 |
|---|---|
| 冒泡排序、插入排序、归并排序、计数排序、桶排序、基数排序 | 选择排序、希尔排序、快速排序、堆排序 |
时间复杂度
排序算法的时间复杂度分为最好时间复杂度、平均时间复杂度和最坏时间复杂度。
基于比较的排序算法的时间复杂度下限是 O(nlogn)O(n\log n)O(nlogn)。
二、冒泡排序
冒泡排序多次遍历数组,它比较相邻的元素,将不合顺序的进行交换,每一轮遍历都将下一个最大值放到正确的位置上。本质上,每个元素通过「冒泡」找到自己所属的位置。
经过 iii 次遍历后,数组末尾的 iii 项必然是最大的那 iii 项,因此冒泡排序最多需要遍历 n−1n-1n−1 遍数组就能完成排序。
动画演示:

冒泡排序实现:
// a是待排序数组,n是数组长度
void bubble_sort(int a[], int n) {for (int i = n - 1; i; i--)for (int j = 0; j < i; j++)if (a[j] > a[j + 1]) swap(a[j], a[j + 1]);
}
可以看出,若两个元素相等,则它们之间不会发生交换,因此冒泡排序具有稳定性。
冒泡排序通常被认为是效率最低的排序算法,因为在确定最终的位置前必须交换元素。注意到如果在一轮遍历中没有发生元素交换,就说明数组已经有序,此时可以提前终止以避免后续的无用功。
改进后的冒泡排序如下(又称短冒泡):
void bubble_sort(int a[], int n) {int round = n - 1; // 因为冒泡排序至多n-1轮遍历就会结束bool flag = true; // flag为false时代表一轮遍历中没有发生元素交换while (round && flag) {flag = false;for (int i = 0; i < round; i++)if (a[i] > a[i + 1]) {flag = true;swap(a[i], a[i + 1]);}round--;}
}
分析时间复杂度。若数组已经是有序的,则冒泡排序只需遍历一遍数组,不用执行任何交换操作,时间复杂度为 O(n)O(n)O(n)。显然冒泡排序的平均时间复杂度和最坏时间复杂度均为 O(n2)O(n^2)O(n2),且在最坏情况下,冒泡排序需要执行 n(n−1)/2n(n-1)/2n(n−1)/2 次交换操作。
三、选择排序
选择排序在冒泡排序的基础上进行了改进,每次遍历数组时只做一次交换。要实现这一点,选择排序在每次遍历时寻找最小值,并在遍历完后将它放到正确的位置上。第一次遍历后,最小的元素就位;第二次遍历后,第二小的元素就位,以此类推。
📝 当然也可以每次遍历时寻找最大值。
动画演示:

选择排序实现:
void selection_sort(int a[], int n) {for (int i = 0; i < n - 1; i++) {int ith = i;for (int j = i + 1; j < n; j++)if (a[j] < a[ith]) ith = j;swap(a[i], a[ith]);}
}
从代码中可以看出选择排序的最好、平均、最坏时间复杂度均为 O(n2)O(n^2)O(n2)。
选择排序是不稳定的。设有数组 [5,3,3][5,\textcolor{red}{3},\textcolor{green}{3}][5,3,3],第一轮遍历后得到 [3,3,5][\textcolor{green}{3},\textcolor{red}{3},5][3,3,5],第二轮遍历时不会有任何元素交换,可以看到两个 333 的相对位置发生了改变。
四、插入排序
插入排序是一种简单直观的排序算法。它在列表较低的一端(即索引较小的一端)维护一个有序子数组,并逐个将每个新元素「插入」这个子数组。
一个与插入排序相同的操作是打扑克牌时,从牌桌上抓一张牌,按牌面大小插到手牌后,再抓下一张牌。
动画演示:
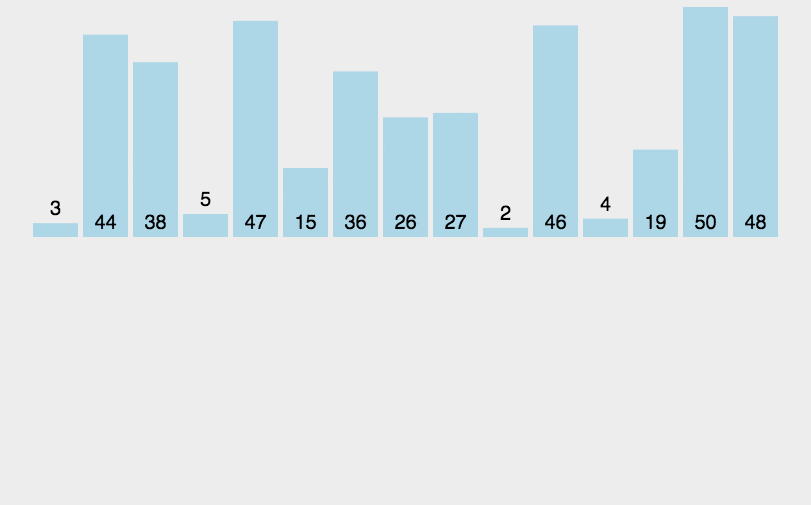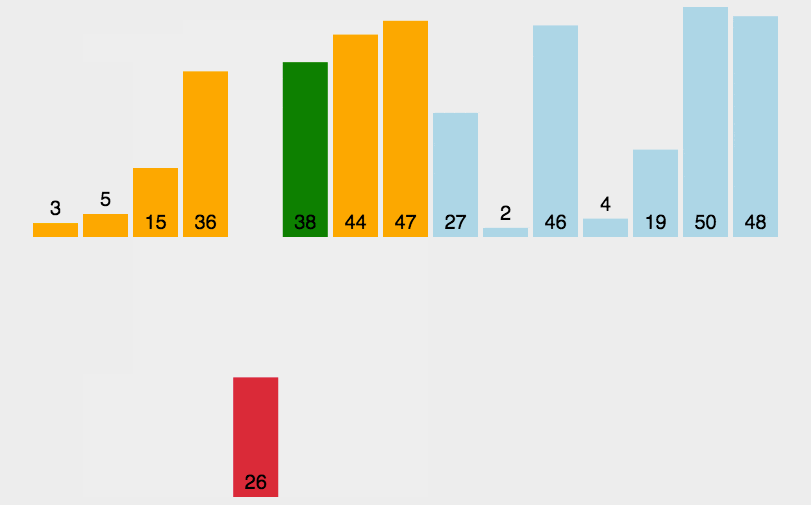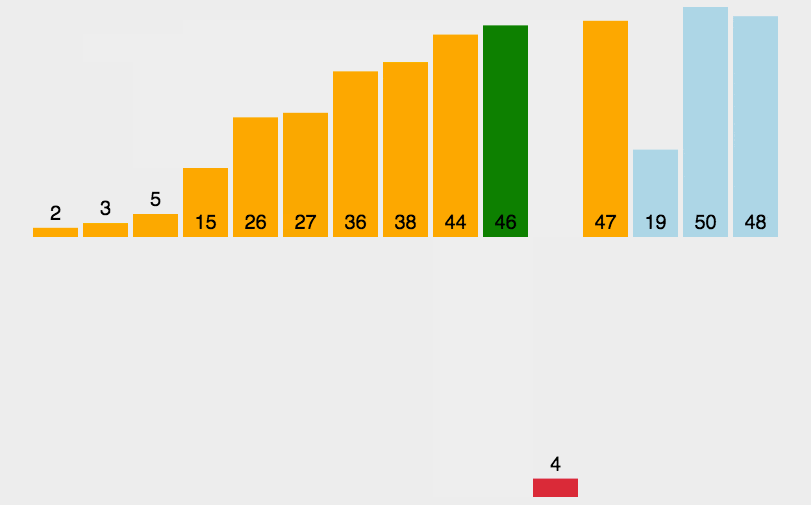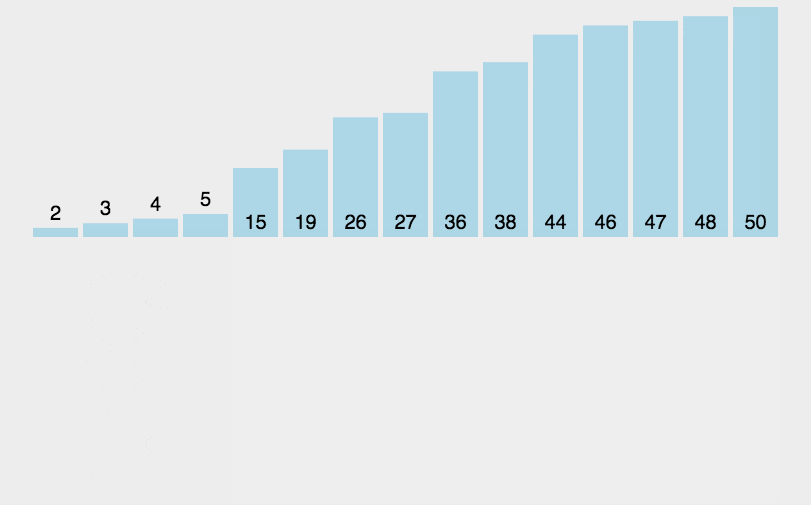
插入排序实现:
void insertion_sort(int a[], int n) {for (int i = 1; i < n; i++) {int key = a[i];int j = i - 1;while (j >= 0 && a[j] > key) {a[j + 1] = a[j];j--;}a[j + 1] = key;}
}
在数组已经是有序的情况下,while 循环不会被执行,因此插入排序的最好时间复杂度为 O(n)O(n)O(n)。显然,插入排序的平均时间复杂度和最坏时间复杂度均为 O(n2)O(n^2)O(n2)。
插入排序是稳定的,因为它会将待插入元素插入到有序子数组中首个发现的大于等于该元素的位置(因为是从右向左遍历,所以首个发现的位置一定靠右),并不会发生交换。
这里再介绍一下二分插入排序。因为数组的左边已经是有序的了,所以可以用二分查找去寻找待插入元素应当插入的位置。<algorithm> 库中有一个 upper_bound 函数,它可以用来查找一个有序序列中首个大于 xxx 的元素,并返回指向该元素的迭代器。
二分插入排序的实现:
void insertion_sort(int a[], int n) {for (int i = 1; i < n; i++) {int key = a[i];int mid = upper_bound(a, a + i, key) - a;for (int j = i - 1; j >= mid; j--) a[j + 1] = a[j];a[mid] = key;}
}
从时间复杂度的角度来看,二分插入排序与直接插入排序相同。
五、对比
三大基础排序算法的比较列在下表中:
| 排序算法 | 最好时间复杂度 | 平均时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O(n)O(n)O(n) | O(n2)O(n^2)O(n2) | O(n2)O(n^2)O(n2) | O(1)O(1)O(1) | 稳定 |
| 选择排序 | O(n2)O(n^2)O(n2) | O(n2)O(n^2)O(n2) | O(n2)O(n^2)O(n2) | O(1)O(1)O(1) | 不稳定 |
| 插入排序 | O(n)O(n)O(n) | O(n2)O(n^2)O(n2) | O(n2)O(n^2)O(n2) | O(1)O(1)O(1) | 稳定 |
References
[1] https://oi-wiki.org/basic/sort-intro/
[2] https://zh.wikipedia.org/wiki/%E6%8E%92%E5%BA%8F%E7%AE%97%E6%B3%95
[3] https://www.runoob.com/w3cnote/ten-sorting-algorithm.html
[4] https://zhuanlan.zhihu.com/p/42586566
相关文章:

三大基础排序算法——冒泡排序、选择排序、插入排序
目录前言一、排序简介二、冒泡排序三、选择排序四、插入排序五、对比References前言 在此之前,我们已经介绍了十大排序算法中的:归并排序、快速排序、堆排序(还不知道的小伙伴们可以参考我的 「数据结构与算法」 专栏)࿰…...
负载均衡上传webshell+apache换行解析漏洞
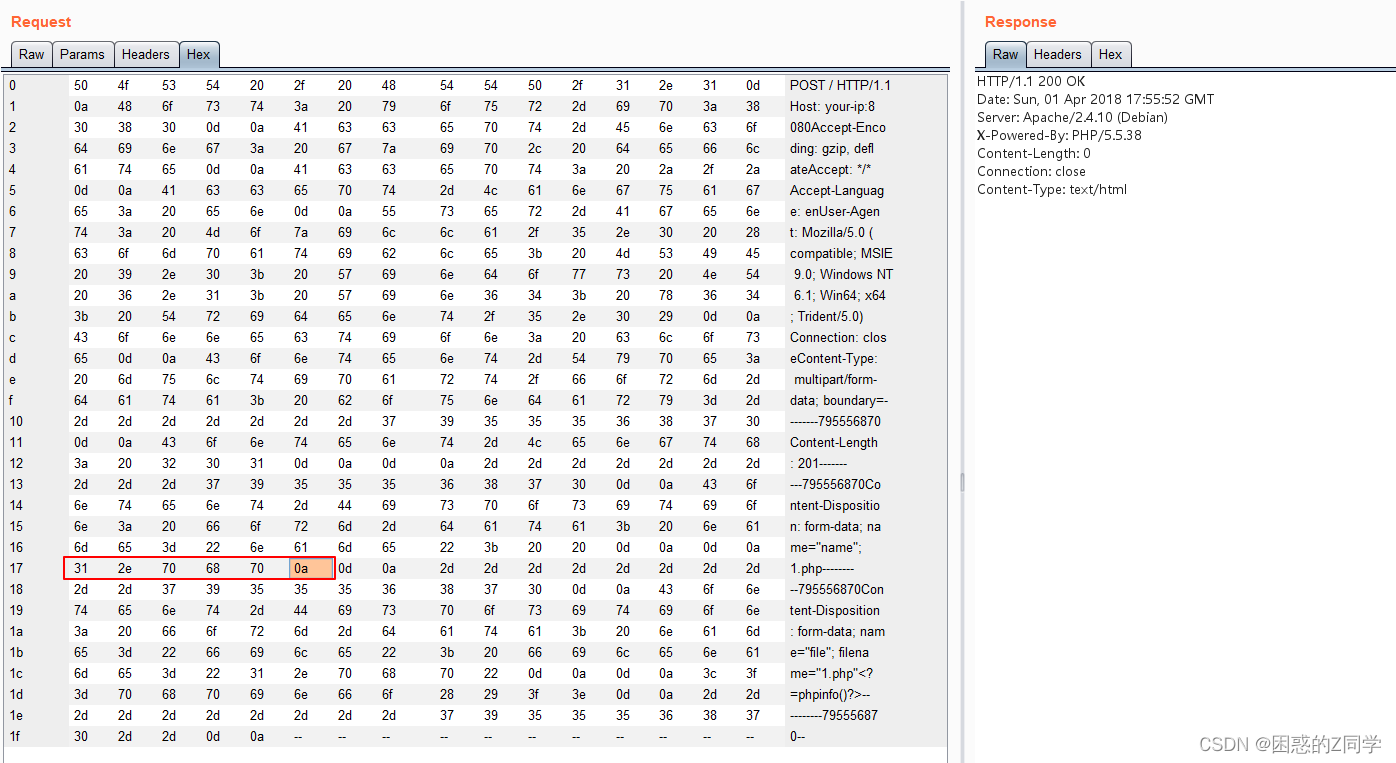
目录一、负载均衡反向代理下的webshell上传1、nginx负载均衡2、负载均衡下webshell上传的四大难点难点一:需要在每一台节点的相同位置上传相同内容的webshell难点二:无法预测下一次请求是哪一台机器去执行难点三:当我们需要上传一些工具时&am…...

【ESP 保姆级教程】玩转emqx数据集成篇③ ——消息重发布
忘记过去,超越自己 ❤️ 博客主页 单片机菜鸟哥,一个野生非专业硬件IOT爱好者 ❤️❤️ 本篇创建记录 2023-02-10 ❤️❤️ 本篇更新记录 2023-02-10 ❤️🎉 欢迎关注 🔎点赞 👍收藏 ⭐️留言📝🙏 此博客均由博主单独编写,不存在任何商业团队运营,如发现错误,请…...
支持分布式部署的主流方式 - Session 持久化到 Redis
1.为什么要将 Session 存储在 Redis 中如果我们不将 Session 存储在 MySQL 或者 Redis 中, 那么做出来的项目就只能支持单机部署, 不支持分布式部署. 因为之前我们只是将 Session 存储在当前电脑的内存里面. 当张三去登录的时候, 将 Session 信息存储在 A 服务器, 这个时候负载…...

计算机网络|第二章 物理层|湖科大课程|从零开始的计网学习——物理层(计网入门就看这篇!)
图片来源于胡科大计算机网络课程,https://www.bilibili.com/video/BV1c4411d7jb?p20&vd_sourcedeb12d86dce7e419744a73045bc66364。文章非盈利商业用途,供博主与大家学习参考,如有侵权,请联系我删除!2.1物理层的基…...
【微服务】RabbitMQSpringAMQP消息队列
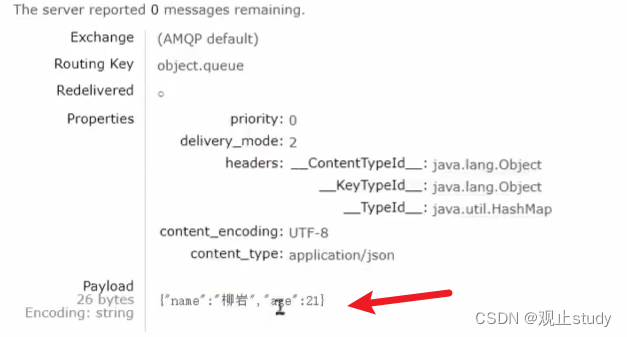
🚩本文已收录至专栏:微服务探索之旅 👍希望您能有所收获 一.初识MQ (1) 引入 微服务间通讯有同步和异步两种方式: 同步通讯:就像打电话,可以立即得到响应,但是你却不能跟多个人同时通话。 异…...

jenkins +docker+python接口自动化之docker下安装jenkins(一)
jenkins dockerpython接口自动化之docker下安装jenkins(一) 目录:导读 1、下载jenkins 2、启动jenkins 3、访问jenkins 4.浏览器直接访问http://ip/:8080 5.然后粘贴到输入框中,之后新手入门中先安装默认的插件即可,完成后出…...
SpringBoot——Banner介绍
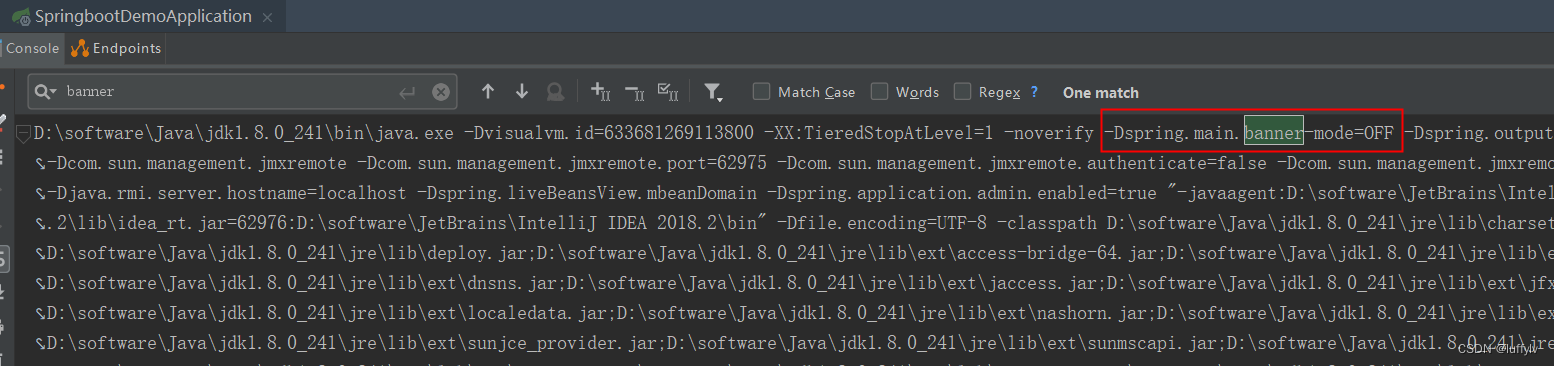
一、什么是BannerBanner即横幅标语,我们在启动SpringBoot项目时会将Banner信息打印至控制台。我们可以输出一些图形、SpringBoot版本信息等内容。默认情况下是通过实现类SpringBootBanner输出的Banner内容,默认的输出内容如下。二、自定义Banner如果不想…...

【STL】综述
STL,一文即可知 文章目录一、STL基本知识概述容器二、序列式容器详述数组容器array向量容器vector双端队列容器deque链式容器list正向链容器forward_list二、关联式容器详述红黑树RB-Tree哈希表参考博客😊点此到文末惊喜↩︎ 一、STL基本知识 概述 STL…...

C++中编译的静态库与动态库
1.什么是库库是写好的现有的,成熟的,可以复用的代码。现实中每个程序都要依赖很多基础的底层库,不可能每个人的代码都从零开始,因此库的存在意义非同寻常。本质上来说库是一种可执行代码的二进制形式,可以被操作系统载…...

JS对象到原始值的转换
JS对象到原始值转换的复杂性 主要由于某些对象类型存在不止一种原始值的表示 对象到原始值转换的三种基本算法 在解释三种算法前需要了解toString valueOf这两个方法 toString 返回对象的字符串表示Array类的toString方法会将每个元素转换为字符串,再使用逗号作为…...

深度复盘-重启 etcd 引发的异常
作者信息: 唐聪、王超凡,腾讯云原生产品中心技术专家,负责腾讯云大规模 TKE 集群和 etcd 控制面稳定性、性能和成本优化工作。 王子勇,腾讯云专家级工程师, 腾讯云计算产品技术服务专家团队负责人。 概况 作为当前中国…...
------新特性)
2023年春招热点面试题(一)------新特性
文章目录一、Spring 6.0 新特性二、Spring Boot 3.0 新特性三、JDK 系列 新特性A.**JDK8新特性(2014年初)(LTS版本)**B. **JDK9新特性(2017年9月)**C.**JDK10新特性(2018年3月)**D.*…...

工程项目管理系统源码+spring cloud 系统管理+java 系统设置+二次开发
工程项目各模块及其功能点清单 一、系统管理 1、数据字典:实现对数据字典标签的增删改查操作 2、编码管理:实现对系统编码的增删改查操作 3、用户管理:管理和查看用户角色 4、菜单管理:实现对系统菜单的增删改查操…...
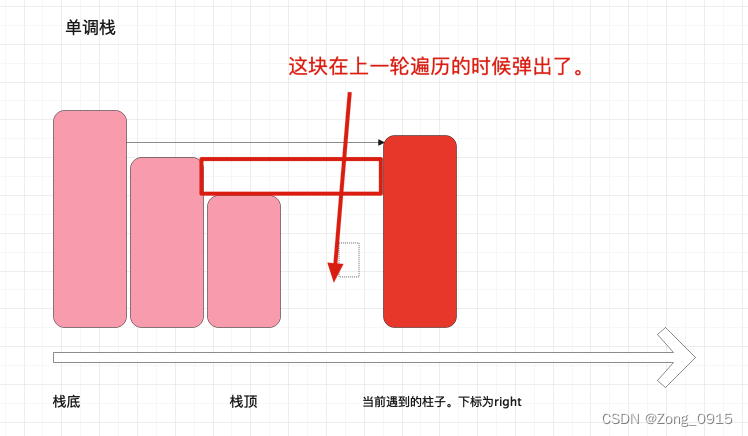
想要精通算法和SQL的成长之路 - 接雨水
想要精通算法和SQL的成长之路 - 接雨水前言一. 接雨水前言 想要精通算法和SQL的成长之路 - 系列导航 一. 接雨水 原题链接 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 输入:height [0,…...
Vue3 更高效的构建工具——Vite
文章目录前言一、Vite简介1. Vite组成2.为什么选 Vite?二、Vite的优缺点vite优点vite缺点三、使用Vite创建Vue3项目1. 创建 vite 的项目2.项目的结构前言 本文讲解了构建工具 Vite,目前只有vue3才可以使用Vite,如果本文对你有所帮助请三连支持博主。 下…...

优思学院|從《狂飙》高启强爱看的《孙子兵法》到六西格玛项目管理
近期最受人瞩目的,无疑是电视剧《狂飙》中出类拔萃的反派高启强。而在剧中,指引高启强走向顶峰的,正是那部著名的军事经典——《孙子兵法》。 在剧中,高启强在一次村庄改造项目上遇到了困难,但他仍保持冷静࿰…...
如何利用状态机编程实现启保停控制(含Stateflow模型介绍)
状态机的介绍这里不再赘述,概念也很简单没有过多的复杂理论。下面我们直接给出具体实现过程。有限自动状态机详细讲解请参看下面的文章链接: PLC面向对象编程系列之有限状态机(FSM)详解_RXXW_Dor的博客-CSDN博客_有限状态机 plc实现编写PLC控制机器动作类程序时,当分支比较…...
4. sql 语句中常用命令
1. 数据表: 本文中所有命令,测试的数据表结构如下图: 2. 查询语句: 2.1 基础查询:select //查询单个字段: select 字段名 from 表名; //查询多个字段 select 字段名1,字段名2,... from 表名; //查询所…...

第三章 Opencv图像像素操作
目录1.像素1-1.确定像素位置1-2.获取指定像素的像素值1-3.修改像素的BGR值2.用numpy模块操作像素2-1.创建图像1.创建黑白图像2.创建彩色图像3.创建随机图像2-2.拼接图像1.水平拼接hstack()方法2.垂直拼接vstack()方法1.像素 1.像素是构成数字图像的最小单位。每一幅图像都是由M…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...
