【图论】单源最短路问题
Dijkstra算法 -- 这是我职业生涯中唯一一个会写,却叫不上名字的算法
Dijkstra算法是一种单源最短路径算法,用于找出图中从一个源点到其他所有点的最短路径。该算法的原理是采用贪心策略,每次将距离源点最近的点加入到已确定最短路径的集合中,并更新其它节点的距离。具体实现过程如下:
-
初始化距离数组dist[],源点距离为0,其余点距离为无穷大。
-
将所有点加入到未确定最短路径的集合中。
-
在未确定最短路径的集合中找出距离源点最近的节点v,并将其加入到已确定最短路径的集合中。
-
对节点v的所有邻居节点u进行更新,如果dist[u] > dist[v] + w(v,u),则更新dist[u] = dist[v] + w(v,u),其中w(v,u)是v到u的边权值。
-
重复步骤3和4,直到所有节点都被加入到已确定最短路径的集合中。
Dijkstra算法的时间复杂度为O(V^2),其中V为节点数。如果使用优先队列来优化实现,时间复杂度可以优化到O(ElogV),其中E为边数。
relax -- 松弛操作
松弛操作是指在图论中,对某个节点的估计值进行更新的过程。通常用于单源最短路径算法,例如Dijkstra算法和Bellman-Ford算法中。具体来说,当我们使用Dijkstra算法或Bellman-Ford算法计算从源节点到其他节点的最短路径时,我们维护一个估计值列表,表示从源节点到每个节点的距离估计,随着算法的执行,我们逐步更新这个列表,直到找到最短路径。
对于Dijkstra算法,我们通过选择距离源节点最近的未标记节点来进行松弛操作,并更新源节点到该节点的距离估计值。以节点u为例,假设当前我们已经确定从源节点到节点u的距离估计值为d[u],而节点u有一个邻居节点v,且u和v之间有一条边e(u,v),边e(u,v)的权重为w(u,v),我们可以通过以下方式来更新v的距离估计值:
d[v] = min(d[v], d[u] + w(u,v))
其中,min表示取两个值的较小值,即如果u到v的距离比当前估计值更短,则更新d[v]为新的估计值。
对于Bellman-Ford算法,我们对所有的边进行松弛操作,直到不能再进行更新为止。以边e(u,v)为例,我们可以通过以下方式来更新v的距离估计值:
if d[u] + w(u,v) < d[v]:
d[v] = d[u] + w(u,v)
其中,if语句的意思是,如果u到v的距离比当前估计值更短,则更新d[v]为新的估计值。
需要注意的是,Bellman-Ford算法可以处理负权边,而Dijkstra算法只适用于图中没有负权边的情况。
相关文章:

【图论】单源最短路问题
Dijkstra算法 -- 这是我职业生涯中唯一一个会写,却叫不上名字的算法 Dijkstra算法是一种单源最短路径算法,用于找出图中从一个源点到其他所有点的最短路径。该算法的原理是采用贪心策略,每次将距离源点最近的点加入到已确定最短路径的集合中…...
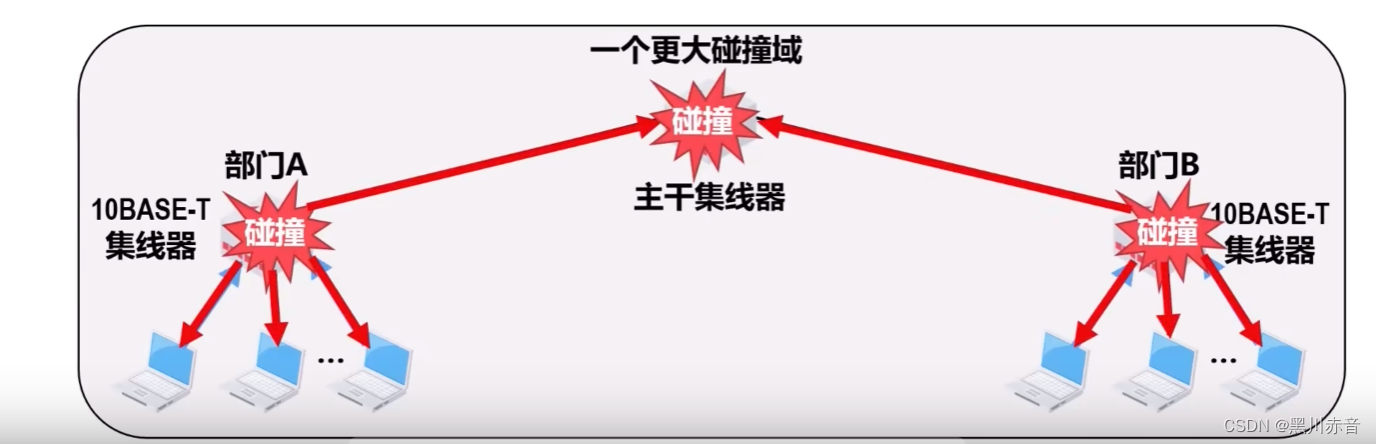
物理层扩展以太网
扩展站点与集线器之间的距离: 在10BASE-T星型以太网中,可使用光纤和一对光纤调制解调器来扩展站点与集线器之间的距离。 为站点和集线器各增加一个用于电信号和光信息号转换的光纤调制解调器,以及他们之间的通信光纤。 扩展共享式以太…...
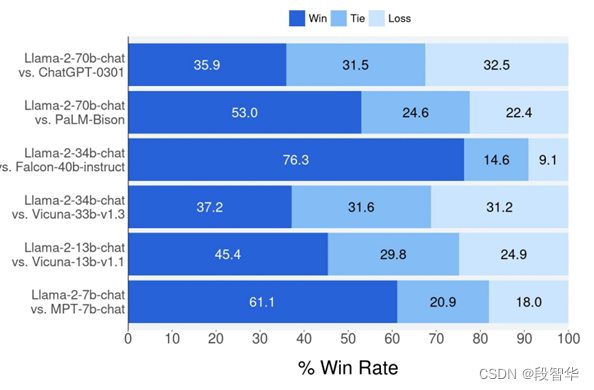
Llama 2 with langchain项目详解(一)
Llama 2 with langchain项目详解(一) 2023年2月25日,美国Meta公司发布了Llama 1开源大模型。随后,于2023年7月18日,Meta公司发布了Llama 2开源大模型,该系列包括了70亿、130亿和700亿等不同参数规模的模型。相较于Llama 1,Llama 2的训练数据增加了40%,上下文长度提升至…...
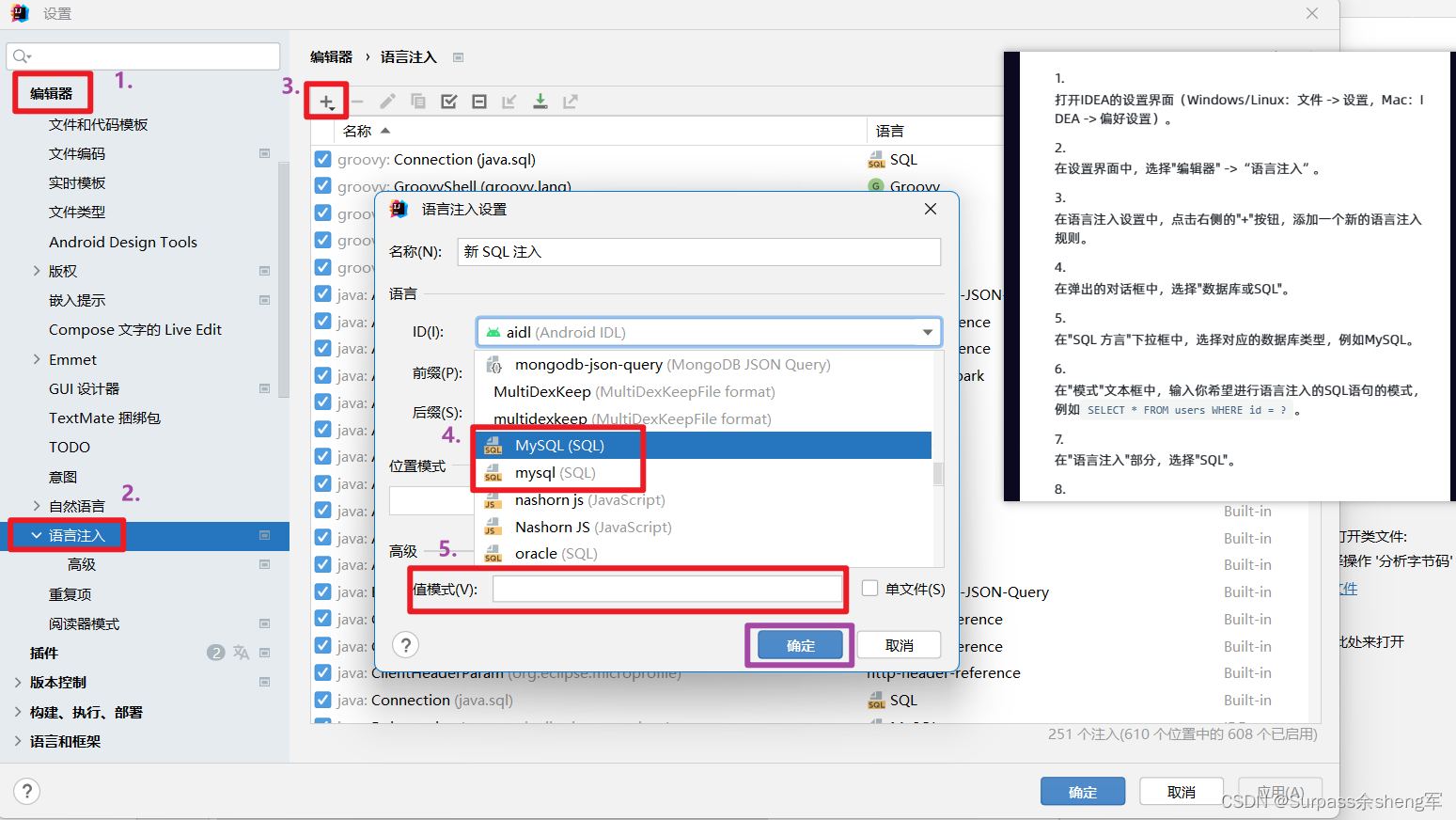
IDEA全局设置MyBatis中写SQL语句提示
把这两个设置改成MySQL即可:...

Linux 内存管理
顾名思义,Liunx内存管理子系统在系统中负责管理内存。它包括虚拟内存管理、段与页的实现、内核态与用户空的空间分配、将文件映射到进程空间等,很多很多酷炫的功能。 Linux内存管理是一个非常复杂的系统,它有非常多的可配置项。大部份这些配置…...

oracle怎样给某个普通用户授予杀自己用户会话的权限
一 问题描述 想给某个普通用户授予杀掉自己会话的权限 二 解决办法 2.1 用sys用户创建杀会话的存储过程 create or replace procedure scott_p_kill_session( v_sid number, v_serial number )asv_varchar2 varchar2(100);beginif v_sid is not null and v_serial is not n…...

redis的主从复制,哨兵和cluster集群
目录 一、redis的高可用 1)redis高可用的概念 2)Redis的高可用技术 二、redis主从复制 1)主从复制的作用 2)主从复制流程 三、redis一主二从的部署 实验组件 实验步骤 环境准备 修改内核参数 安装 Redis 创建redis工…...
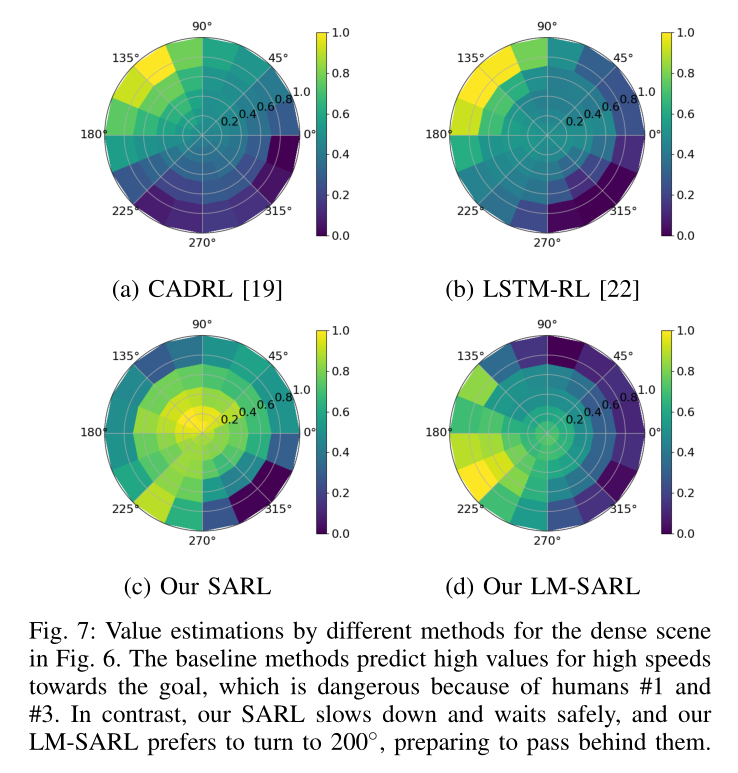
Crowd-Robot Interaction 论文阅读
论文信息 题目:Crowd-Robot Interaction:Crowd-aware Robot Navigation with Attention-based Deep Reinforcement Learning 作者:Changan Chen, Y uejiang Liu 代码地址:https://github.com/vita-epfl/CrowdNav 来源:arXiv 时间…...

什么是LIMS系统,LIMS实验室管理系统
LIMS是实验室信息管理系统,全称是Laboratory Information Management System,是将以数据库为核心的信息化技术与实验室管理需求相结合的信息化管理工具。它是由计算机硬件和应用软件组成,能够完成实验室数据和信息的收集、分析、报告和管理&a…...
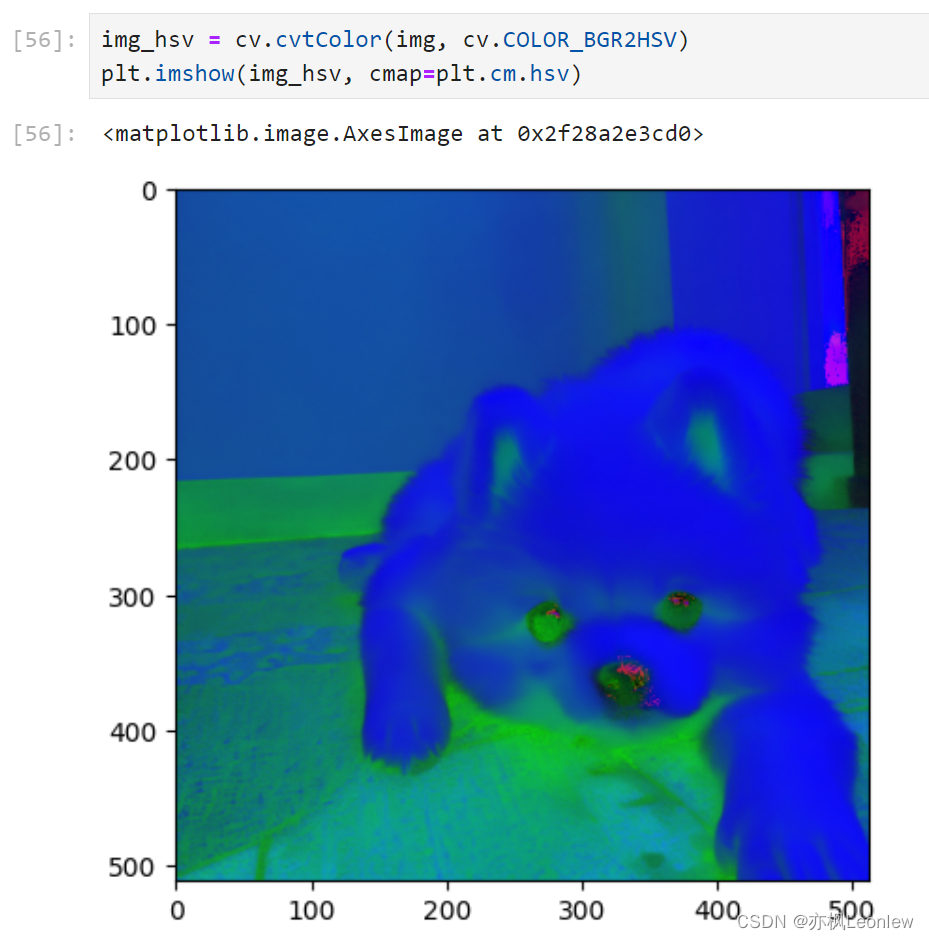
Python Opencv实践 - 图像属性相关
import numpy as np import cv2 as cv import matplotlib.pyplot as pltimg cv.imread("../SampleImages/pomeranian.png", cv.IMREAD_COLOR) plt.imshow(img[:,:,::-1])#像素操作 pixel img[320,370] print(pixel)#只获取蓝色通道的值 pixel_blue img[320,370,0]…...

PCB制造中铜厚度的重要性
电子产品中的PCB是现代电子设备中不可或缺的一部分。在PCB制造过程中,铜厚度是一个非常重要的因素。正确的铜厚度可以保证电路板的质量和性能,同时也影响着电子产品的可靠性和稳定性。 一般我们常见的铜厚有17.5um(0.5oz)&#x…...
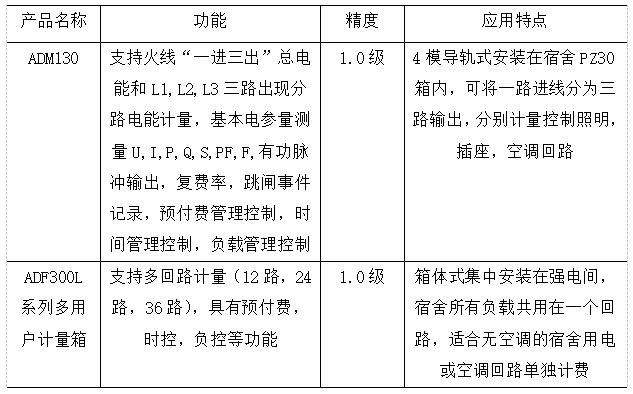
浅谈高校宿舍水电表远程智能管理的研究与应用
安科瑞 华楠 摘要:本系统的设计是基于485总线技术与TCP/IP网络技术相结合的方式来实现的,充分考虑了目前高校后勤水电表管理控制的实际情况,以传输可靠性高、技术成熟、成本低的485总线技术为基础,并与应用广泛的TCP/IP网络相结合…...
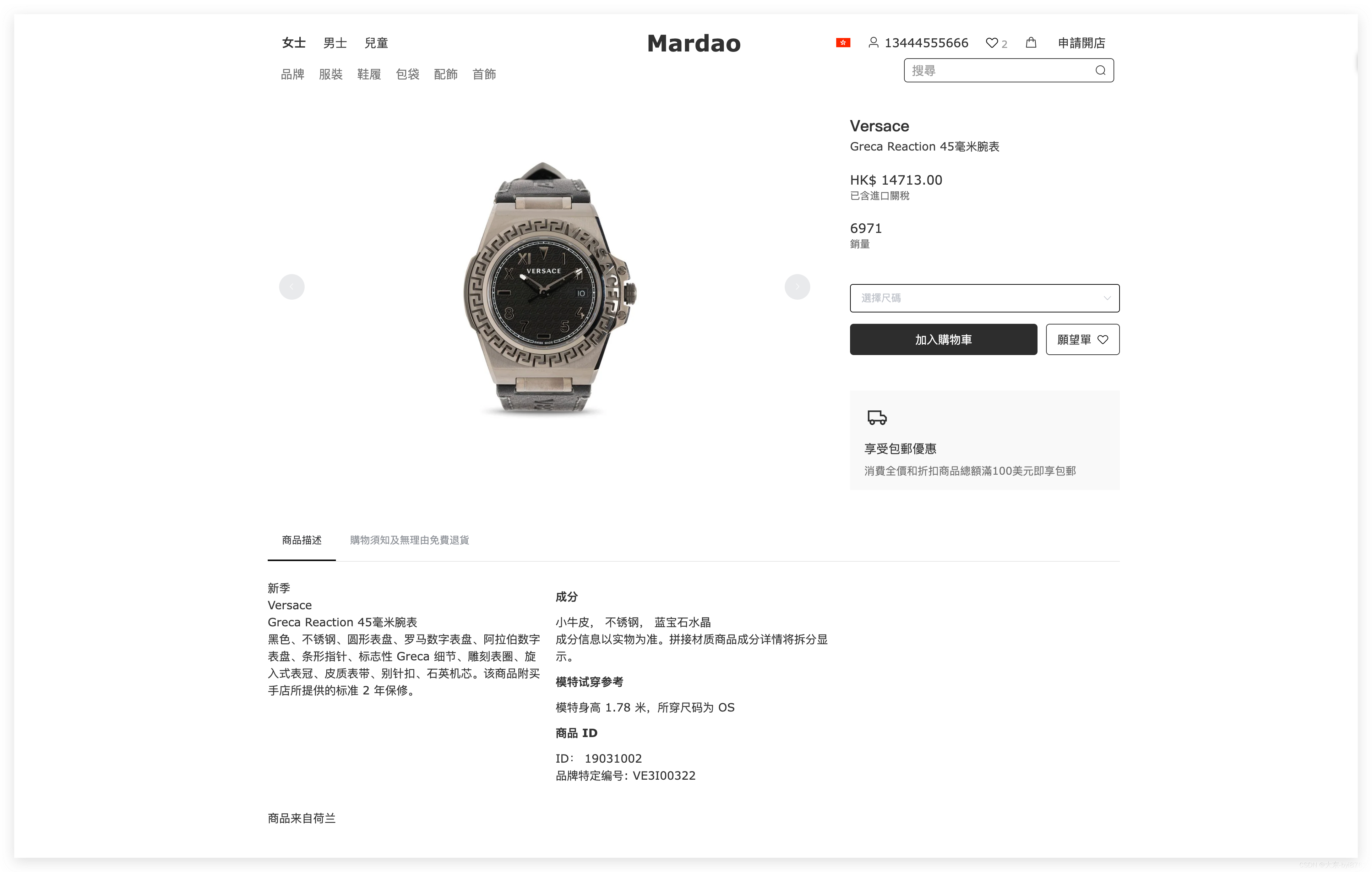
无货源跨境电商购物平台快速搭建(微商城、小程序、APP、网站)
无货源跨境电商购物平台的快速搭建可以通过以下步骤完成,并且可以同时开发微商城、小程序、APP和网站以满足不同用户的需求。 第一步:需求分析 在搭建之前,需要对平台的需求进行详细的分析。包括用户需求、功能需求、技术需求等等。这一步是…...
)
力扣:57. 插入区间(Python3)
题目: 给你一个 无重叠的 ,按照区间起始端点排序的区间列表。 在列表中插入一个新的区间,你需要确保列表中的区间仍然有序且不重叠(如果有必要的话,可以合并区间)。 来源:力扣(LeetC…...
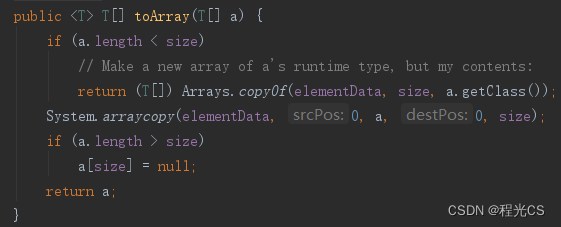
List和数组互转方法以及踩坑点
一、数组转List 1. 使用for循环逐个添加 String[] array {"A", "B", "C"}; List<String> list new ArrayList<>(); for (String element : array) {list.add(element); }2. 使用Arrays.asList(arr) String[] array {"A&q…...

css3背景渐变
1.线性渐变 <style>.box {width: 200px;height: 200px;border: 1px solid black;float: left;margin-left: 50px;}.box1 {background-image: linear-gradient(green, yellow, red);}/* 右上 */.box2 {background-image: linear-gradient(to right top, green, yellow, re…...
windows 安装免费3用户ccproxy ubuntu 代理上网
Windows 上进行安装 ubuntu 上进行设置 方法一 (临时的手段) 如果仅仅是暂时需要通过http代理使用apt-get,您可以使用这种方式。 在使用apt-get之前,在终端中输入以下命令(根据您的实际情况替换yourproxyaddress和proxyport)。 终…...

B树的插入与删除过程
B树的插入 原树: 插入key后,若导致原节点关键字数超过上限,则从中间位置( ⌈ m 2 ⌉ \lceil\frac{m}{2}\rceil ⌈2m⌉)将关键字分成两部分,左部分包含的关键字放在原节点中,右部分包含的关键…...
【二分】CF1623 C
Problem - 1623C - Codeforces 题意: 思路: 肯定是二分,我们去二分最小值,然后check的时候最小值要大于mid check的时候要让最小值尽可能大 注意到我们不需要去管最大值,只需要最小值尽可能大就好了,因…...
)
redis五大类型分析--list(1)
此篇为对redis五大数据类型中list的分析,希望能有所帮助 List API listTypePush函数 void listTypePush(robj *subject, robj *value, int where) {/* 检查编码类型是否为 quicklist (快速列表) */if (subject->encoding OBJ_ENCODING_QUICKLIST) {/* 根据参数…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...

React父子组件通信:Props怎么用?如何从父组件向子组件传递数据?
系列回顾: 在上一篇《React核心概念:State是什么?》中,我们学习了如何使用useState让一个组件拥有自己的内部数据(State),并通过一个计数器案例,实现了组件的自我更新。这很棒&#…...

五、jmeter脚本参数化
目录 1、脚本参数化 1.1 用户定义的变量 1.1.1 添加及引用方式 1.1.2 测试得出用户定义变量的特点 1.2 用户参数 1.2.1 概念 1.2.2 位置不同效果不同 1.2.3、用户参数的勾选框 - 每次迭代更新一次 总结用户定义的变量、用户参数 1.3 csv数据文件参数化 1、脚本参数化 …...

LeetCode 0386.字典序排数:细心总结条件
【LetMeFly】386.字典序排数:细心总结条件 力扣题目链接:https://leetcode.cn/problems/lexicographical-numbers/ 给你一个整数 n ,按字典序返回范围 [1, n] 内所有整数。 你必须设计一个时间复杂度为 O(n) 且使用 O(1) 额外空间的算法。…...

以太网PHY布局布线指南
1. 简介 对于以太网布局布线遵循以下准则很重要,因为这将有助于减少信号发射,最大程度地减少噪声,确保器件作用,最大程度地减少泄漏并提高信号质量。 2. PHY设计准则 2.1 DRC错误检查 首先检查DRC规则是否设置正确,然…...
