css的transform样式计算-第一节
本文作者为 360 奇舞团前端开发工程师
引言
在使用 css 样式进行样式的缩放、旋转等设置时,思考了一下它的较浅层的原理,恩,这个阶段都 是一些初高的数学计算,从新看这里的时候顺便捡了捡初高中的数学,比如三角函数之类。
通用公式
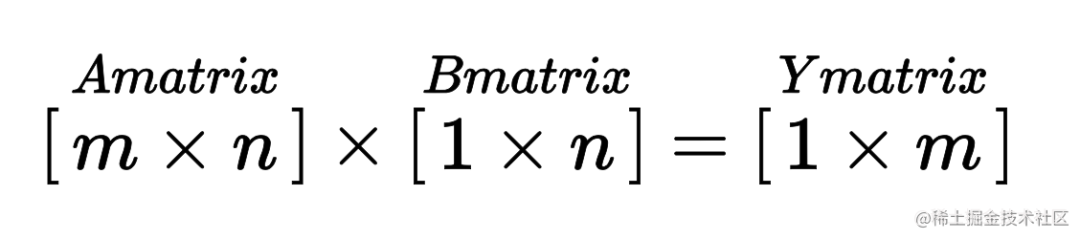
假设 A * B = Y。其中,A 为 m * n 的 m 行 n 列矩阵,B 为 1 * n 列的矩阵。B 拆分为列向量,并且列向量的维数就是矩阵的行数。
方法
transform(a, b, c, d, e, f) 与 Matrix 的转换。
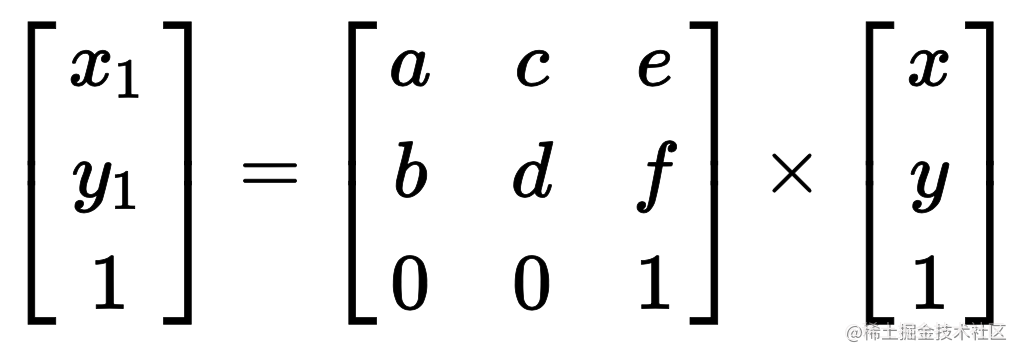
推导出来
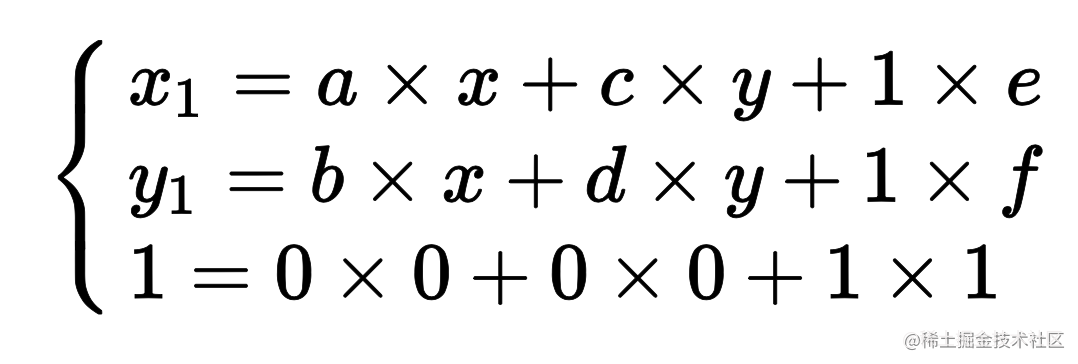
简化后
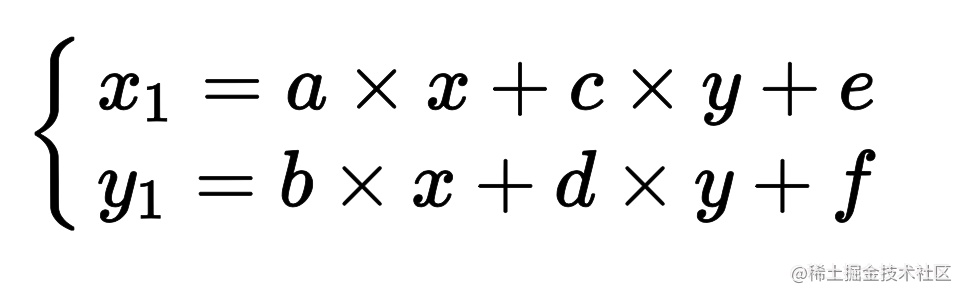
缩放
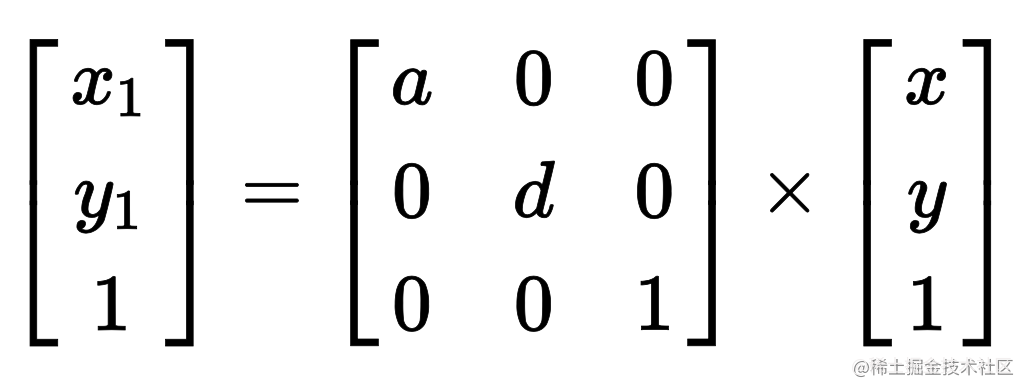
推导出来
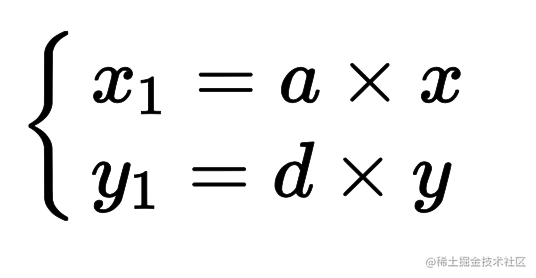
.box {transform: scale(0.3, 0.6);
}通过计算
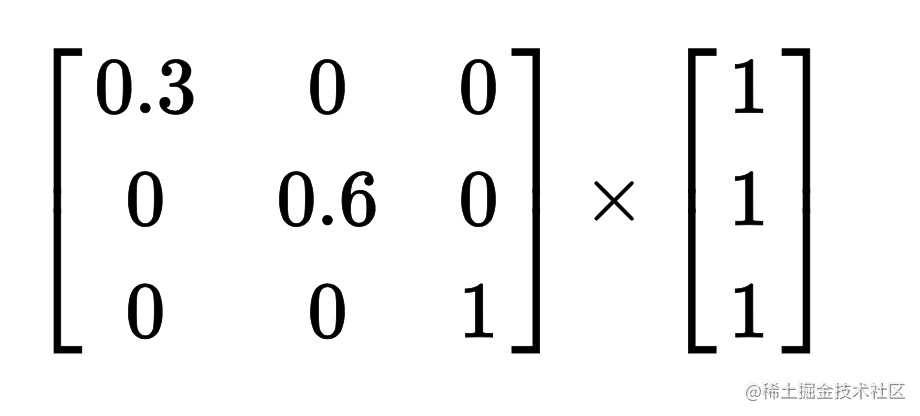
等价于
.box {transform: matrix(0.3, 0, 0, 0.6, 0, 0);
}
平移
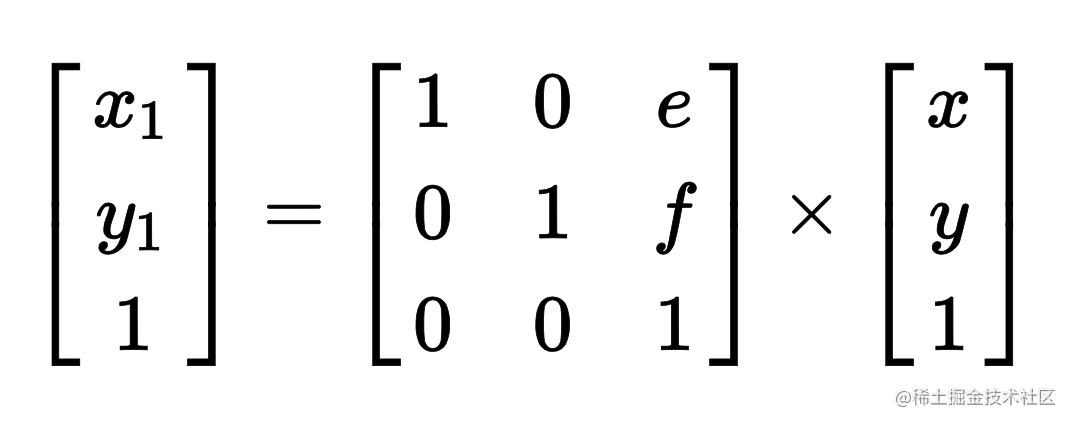
推导出来
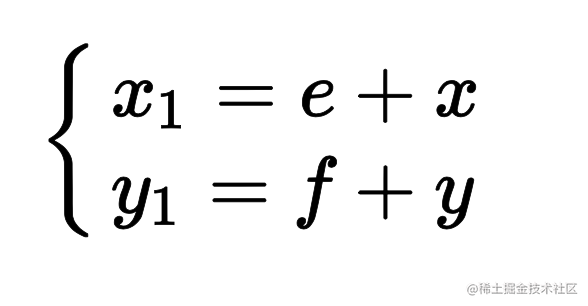
转旋

推导出来
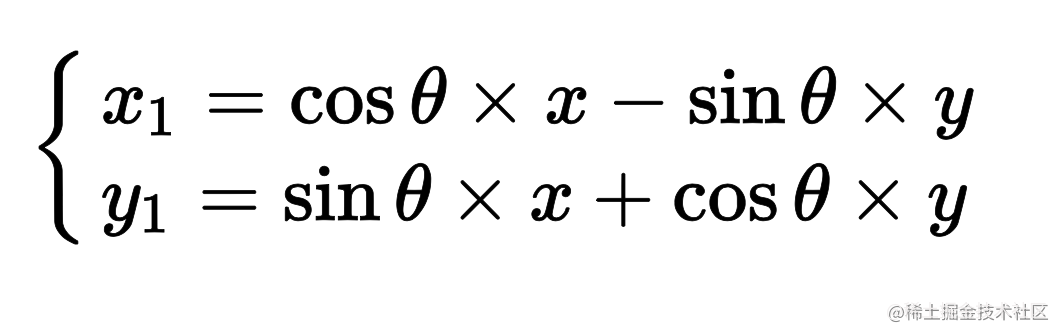
假设存在点 E 移动至点 F。设 E 坐标为(x1, y1),F 坐标为(x2, y2),D 坐标为(a, b)。
简要图示:
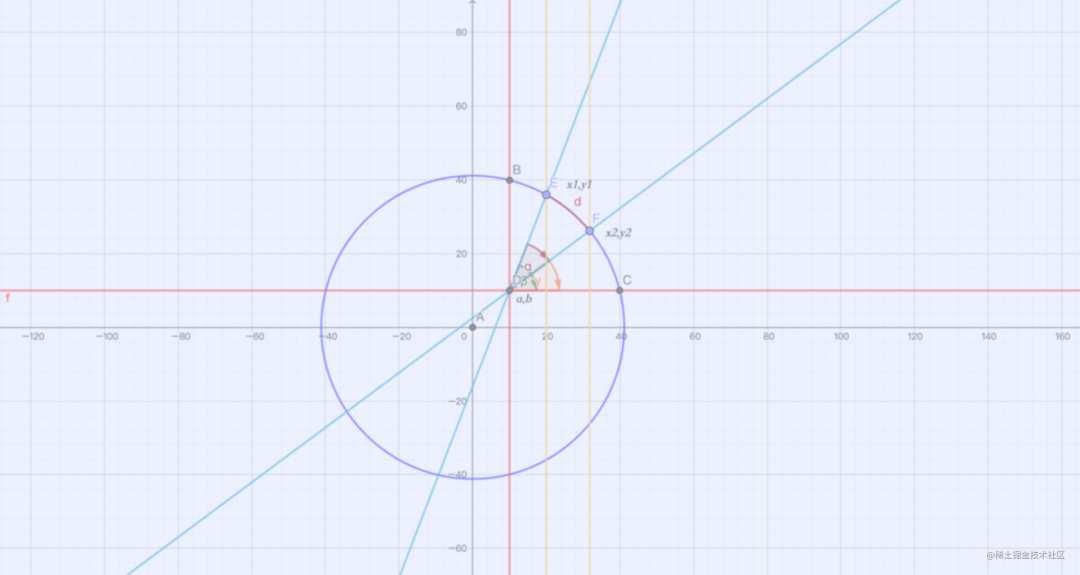
初中数学:
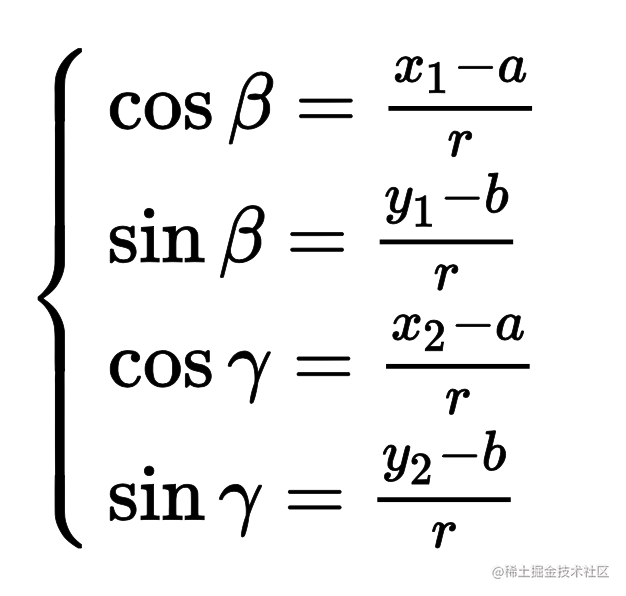
演算:
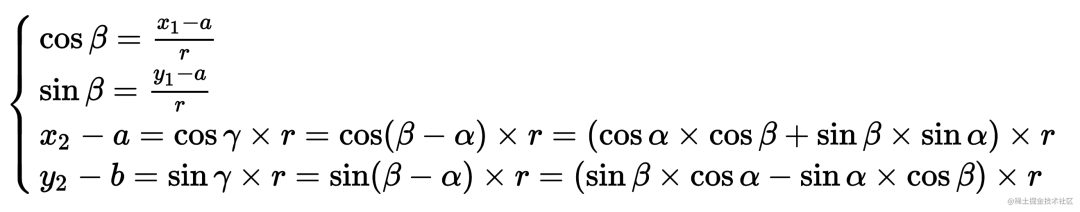
推导:
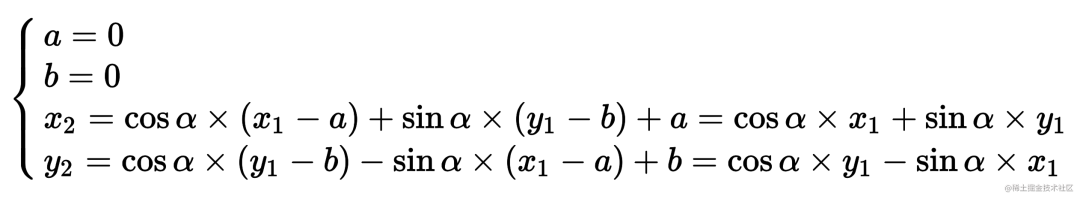
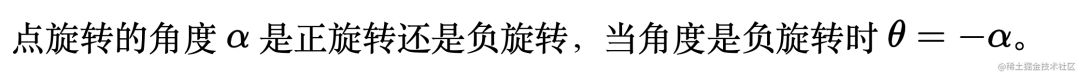
验证:
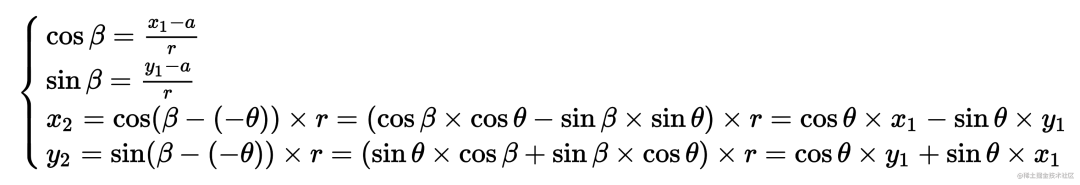
转换为矩阵:
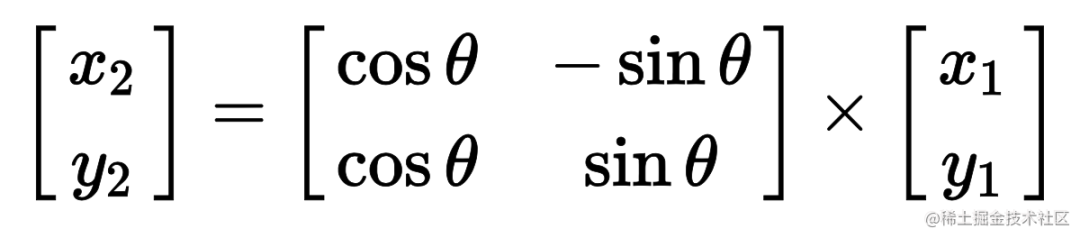
从 css 语法上开始转换
.box {transform: rotate(30deg);
}这个旋转套用公式
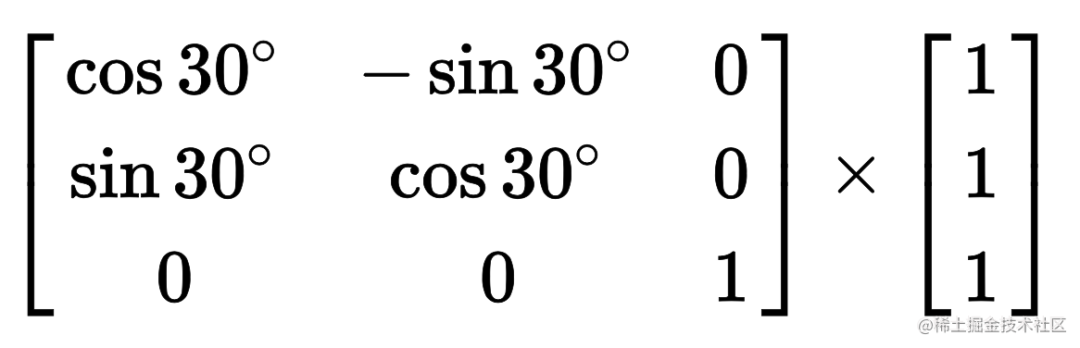
等价于
.box {transform: matrix(0.86, 0.5, -0.5, 0.86, 0, 0);
}
复合
.box {transform: rotate(30deg) scale(0.3, 0.6);
}复合需要进行矩阵乘法计算

等价于
.box {transform: matrix(0.258, 0.15, -0.3, 0.516, 0, 0);
}最后,后续本文修正和更新,请参阅:'https://kangkk.cn/index.php/计算机原理/仿射变换'
- END -
关于奇舞团
奇舞团是 360 集团最大的大前端团队,代表集团参与 W3C 和 ECMA 会员(TC39)工作。奇舞团非常重视人才培养,有工程师、讲师、翻译官、业务接口人、团队 Leader 等多种发展方向供员工选择,并辅以提供相应的技术力、专业力、通用力、领导力等培训课程。奇舞团以开放和求贤的心态欢迎各种优秀人才关注和加入奇舞团。

相关文章:

css的transform样式计算-第一节
本文作者为 360 奇舞团前端开发工程师 引言 在使用 css 样式进行样式的缩放、旋转等设置时,思考了一下它的较浅层的原理,恩,这个阶段都 是一些初高的数学计算,从新看这里的时候顺便捡了捡初高中的数学,比如三角函数之类…...

C++中vector、list和deque的选择:什么时候使用它们?
系列文章目录 文章目录 系列文章目录前言一、vector二、list三、deque总结 前言 在C中,vector、list和deque是STL(标准模板库)提供的三种常见的容器。每种容器都有其特点和适用场景。本文将详细介绍vector、list和deque的特点以及它们的适用…...

【力扣每日一题】2023.8.10 下降路径最小和Ⅱ
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 题目给我们一个数组,让我们模拟从上面第一层走到下面的最后一层,下降路径需要加上经过的格子的值,每层…...
)
gh-ost概述(二实践)
注意:只适用于拥有主键或者唯一键的表,不存在触发器的表 一、gh-ost的安装部署 0、yum -y install golang 1、进入官网GitHub - github/gh-ost: GitHub’s Online Schema-migration Tool for MySQL 2、下载gh-ost-master.zip包 3、解压unzip gh-ost-mast…...
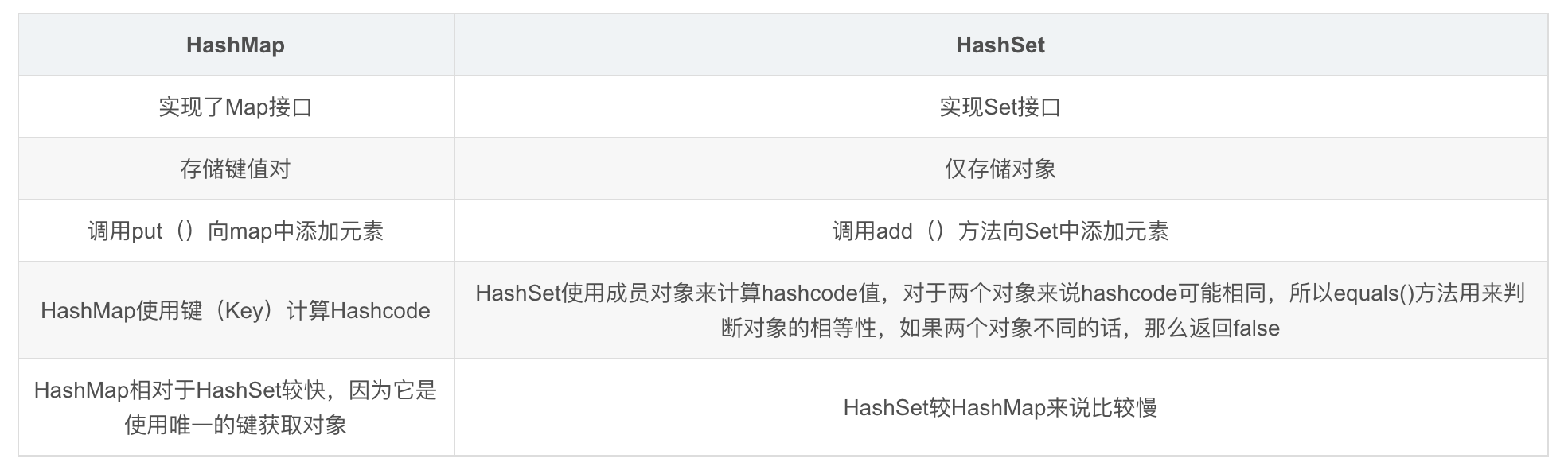
临时文档3
Set接口 说一下 HashSet 的实现原理? HashSet 是基于 HashMap 实现的,HashSet的值存放于HashMap的key上,HashMap的value统一为PRESENT,因此 HashSet 的实现比较简单,相关 HashSet 的操作,基本上都是直接调…...

【OpenGauss源码学习 —— 执行算子(SeqScan算子)】
执行算子(SeqScan算子) 执行算子概述扫描算子SeqScan算子ExecInitSeqScan函数InitScanRelation函数ExecSeqScan函数 总结 声明:本文的部分内容参考了他人的文章。在编写过程中,我们尊重他人的知识产权和学术成果,力求遵…...
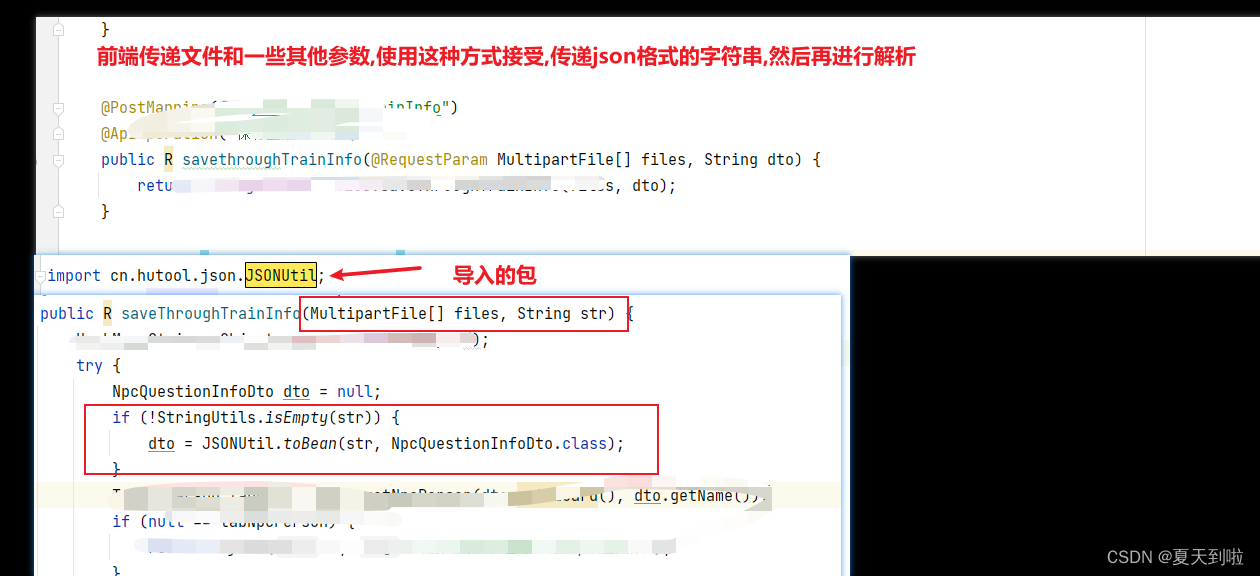
Postman中,既想传递文件,还想传递多个参数(后端)
需求:既想传文件又想传多个参数可以用以下方式实现...

跨境干货|TikTok变现的9种方法
在这个流量为王的时代,哪里有流量,哪里就有商机。TikTok作为近几年最火爆的社媒平台之一,在全球范围都具有一定的影响力。随着TikTok Shop等商务功能加持上线,更是称为跨境电商的新主场之一。 在这样的UGC平台,想要变…...
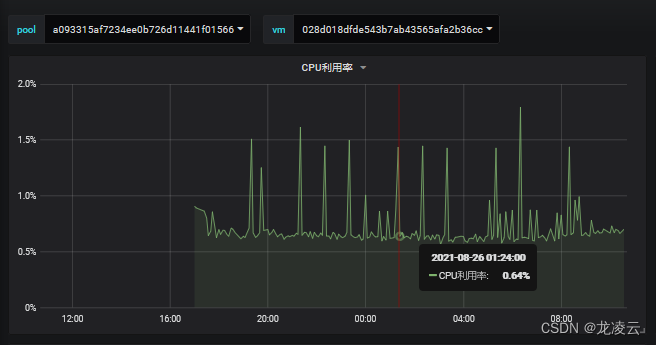
Grafana 曲线图报错“parse_exception: Encountered...”
问题现象 配置的Grafana图报错如下: 原因分析 点开报错,可以看到报错详细信息,是查询语句的语法出现了异常。 变量pool的取值为None 解决方案 需要修改变量pool的查询SQL,修改效果如下: 修改后&#x…...
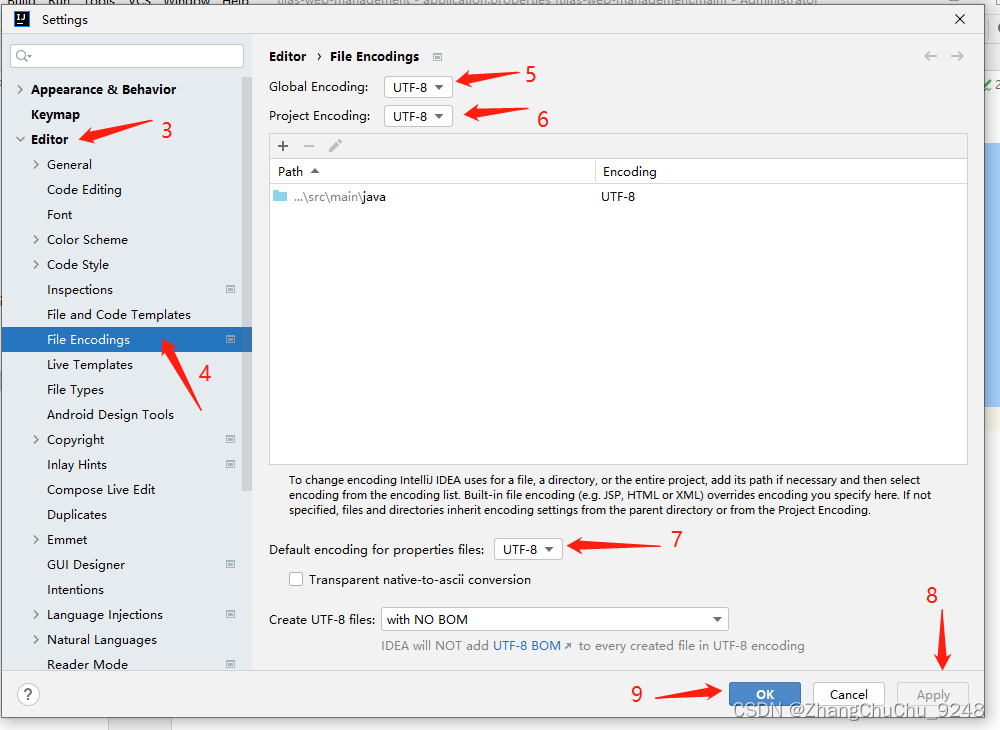
idea中提示Unsupported characters for the charset ‘ISO-8859-1‘
application.properties中文注释拉黄线 ,提示Unsupported characters for the charset ISO-8859-1 解决办法: 注意: 改完之后之前输入的中文就变成“ ???”了,建议备份一下 1、打开setti…...
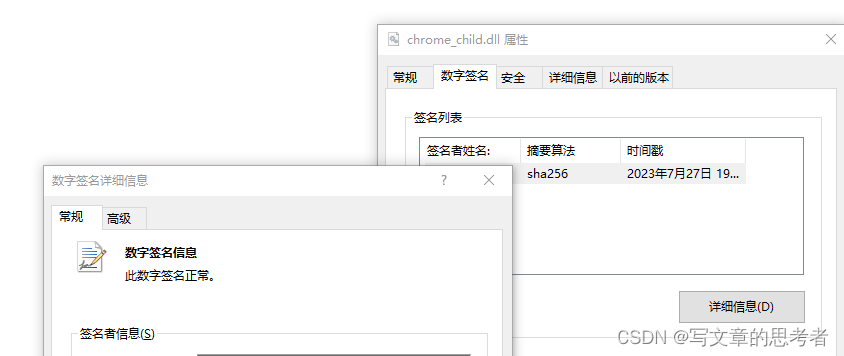
通过signtool进行数字签名和验证签名
(一)如何签名 SignTool.exe (Sign Tool) - .NET Framework | Microsoft Learn Using SignTool to Sign a File - Win32 apps | Microsoft Learn 签名命令行: signtool.exe sign /f xxx.pfx /t http://timestamp.digicert.com yyy.dll xx…...

geeemap学习总结(2)——地图底图应用
1. 加载库中已有图层 import os os.environ[HTTP_PROXY] http://127.0.0.1:8001 os.environ[HTTPS_PROXY] http://127.0.0.1:8001 # 设置中心位置/地图层级/图层加载高度,加载图层 import geemap Mapgeemap.Map(center[40, 100], zoom4, height600) Map# 添加已经…...
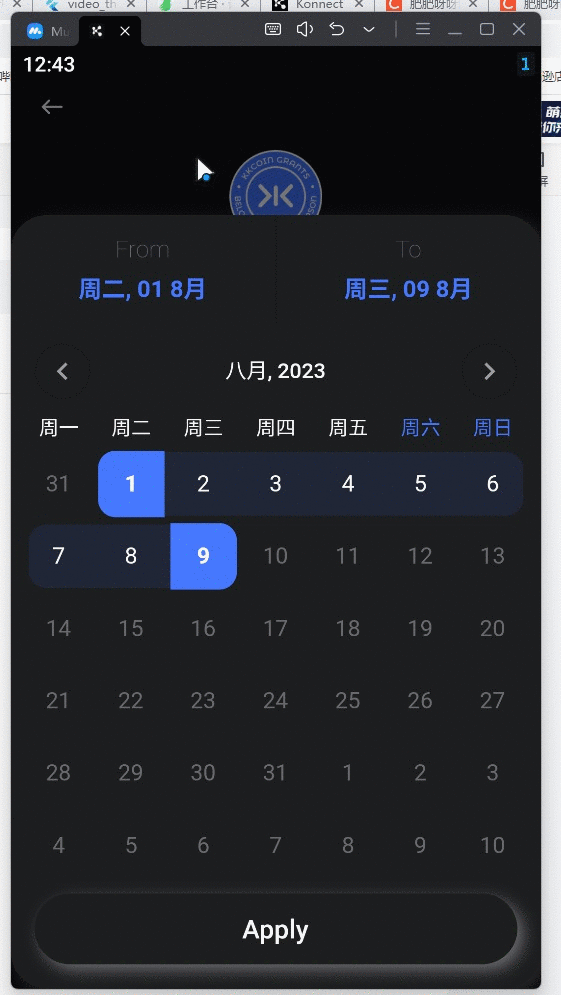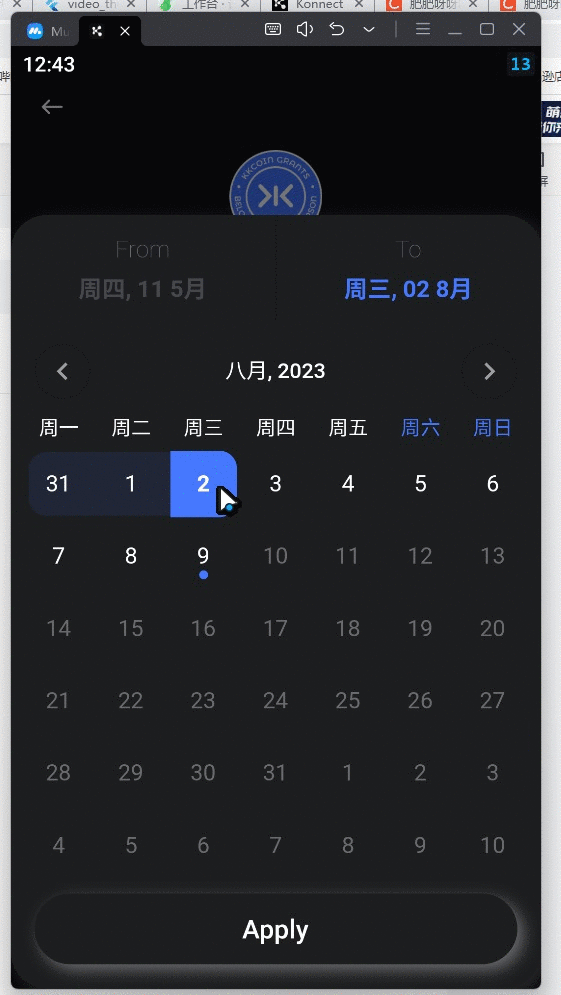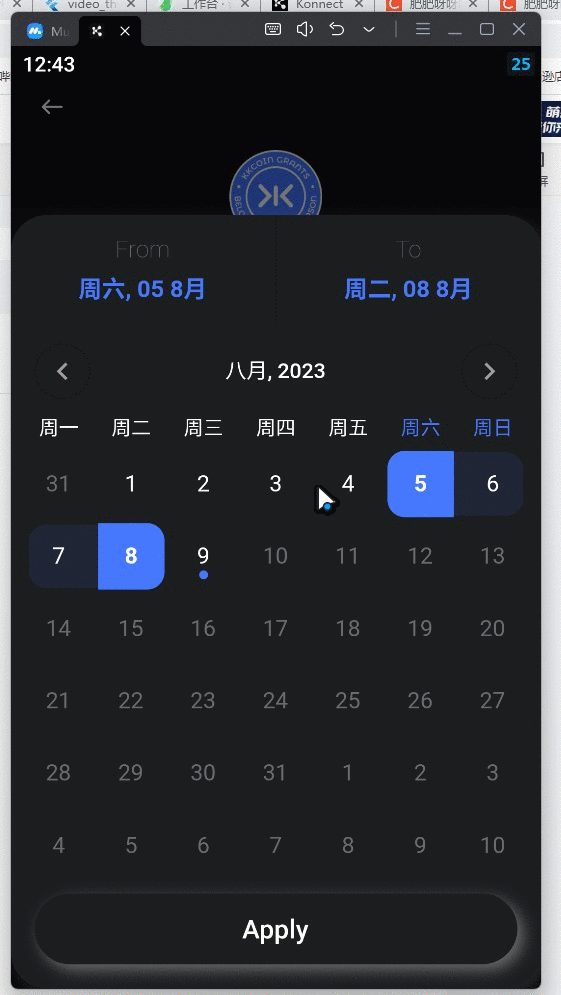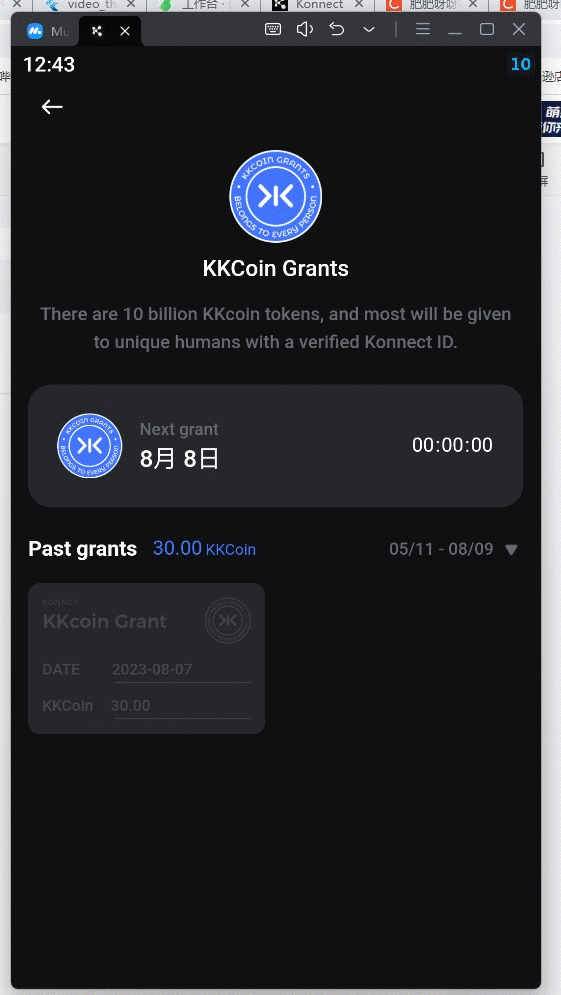
flutter 手写日历组件
先看效果 直接上代码 calendar_popup_view.dart import package:flutter/material.dart; import package:intl/intl.dart;import custom_calendar.dart; import hotel_app_theme.dart;class CalendarPopupView extends StatefulWidget {const CalendarPopupView({required th…...

C++动态规划经典试题解析之打家劫舍系列
1.前言 力扣上有几道与打家劫舍相关的题目,算是学习动态规划时常被提及的经典试题,很有代表性,常在因内大大小小的社区内看到众人对此类问题的讨论。 学习最好的方式便是归纳总结、借鉴消化,基于这个目的,本文对此类问题也做了讲解,在一些优秀思想的基础上添加了个人观…...
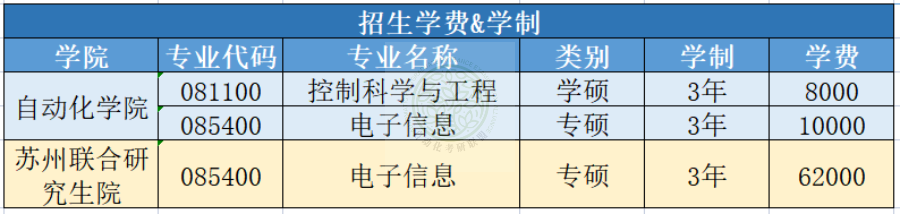
24届近5年东南大学自动化考研院校分析
今天给大家带来的是东南大学控制考研分析 满满干货~还不快快点赞收藏 一、东南大学 学校简介 东南大学是我国最早建立的高等学府之一,素有“学府圣地”和“东南学府第一流”之美誉。东南大学前身是创建于1902年的三江师范学堂。1921年经近代著名教育家…...

electron、electron-forge 安装
npm修改了registry,安装依旧无效 使用cnpm 倒是可以解决,但是 npx electron-forge import 中 Installing dependencies 使用的是npm 给出一次性解决方案: step1:切换npm的下载源,可以使用nrm 进行管理,有…...

go的strings用法
strings 是 Go 语言标准库中提供的一个包,用于处理字符串相关的操作。这个包包含了许多函数,可以用于字符串的切割、拼接、替换、查找等操作。下面是一些常用的 strings 包函数和用法示例: package mainimport ("fmt""string…...
echo用法、linxu课堂练习题、作业题
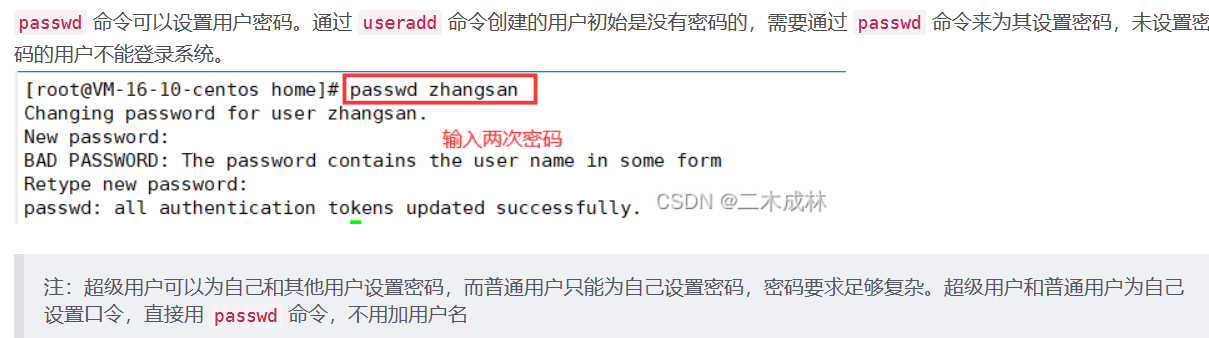
一、课堂练习 练习一: 4、普通用户修改密码: root修改密码: 5、修改主机名:hostnamectl hostname 主机名 查看:hostnamectl或者cat etc/hostname 练习二: 1、 mkdir /root/html touch /root/html/index.…...

WordPress使用【前端投稿】功能时为用户怎么添加插入文章标签
在使用Wordpress做前端投稿功能的时候,可能需要用户填写文章标签,在插入文章的时候很多人不知道怎么把这些标签插入进去,下面这篇文章来为大家带来WordPress使用前端投稿功能时插入文章标签方法。 在Wordpress里 wp_insert_post 此函数的作…...

第二章:CSS基础进阶-part1:CSS高级选择器
文章目录 一、 组合选择器二、属性选择器三、伪类选择器1、动态伪类选择器2、状态伪类选择器3、结构性伪类选择器4、否定伪类选择器 一、 组合选择器 后代选择器:E F子元素选择器: E>F相邻兄弟选择器:EF群组选择器:多个选择器…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...
