【树和二叉树】数据结构二叉树和树的概念认识
前言:在之前,我们已经把栈和队列的相关概念以及实现的方法进行了学习,今天我们将认识一个新的知识“树”!!!
目录
- 1.树概念及结构
- 1.1树的概念
- 1.2树的结构
- 1.3树的相关概念
- 1.4 树的表示
- 1.5 树在实际中的运用(表示文件系统的目录树结构)
- 2.二叉树概念及结构
- 2.1概念
- 2.2现实中的二叉树
- 2.3 特殊的二叉树
- 2.4 二叉树的性质
- 3.选择题
1.树概念及结构
1.1树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它或为空树(n=0);或为非空树,对于非空树T,具有以下特点:
①.有一个特殊的结点,称为根结点,根节点没有前驱结点,除根节点之外所有结点有且只有一个前驱结点;
②.除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
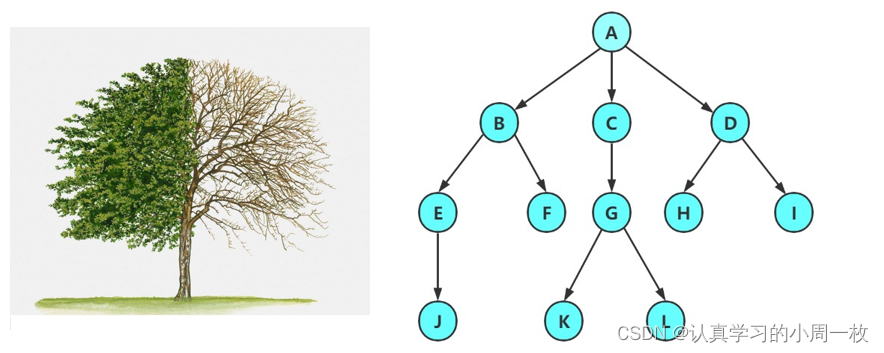
如何理解其中的“子树”呢?我们以下图为例:
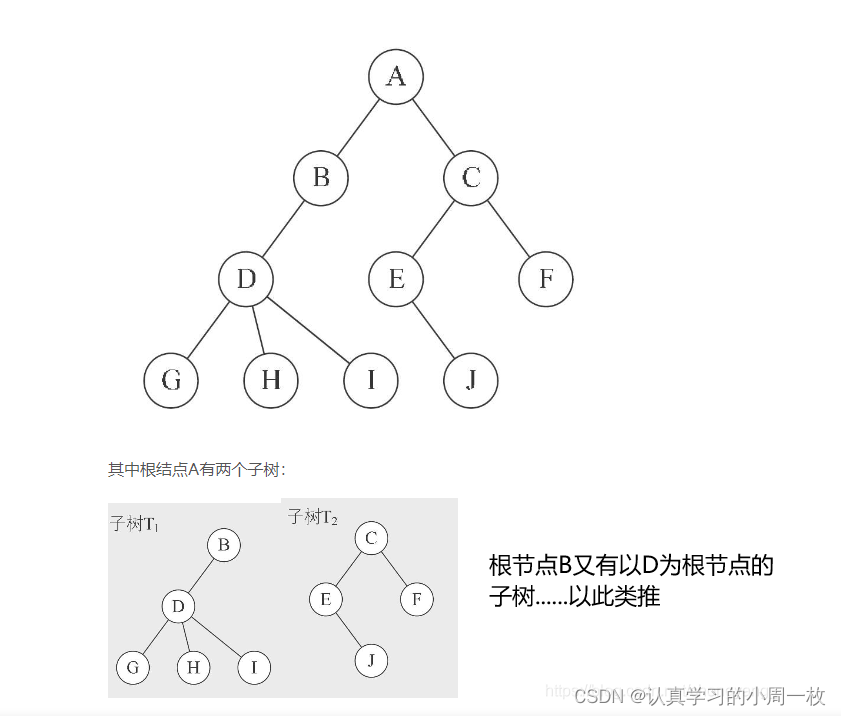
开始时以A为根,我们可以发现A的子树有B和C两棵(即跟A类似的结构),紧接着子树B和C又根据这样的规则在依次向下,因此我们不难发现,任何一棵树都可以分解成根和N棵子树(N>=0)。
因此,可以得出结论树是递归定义的
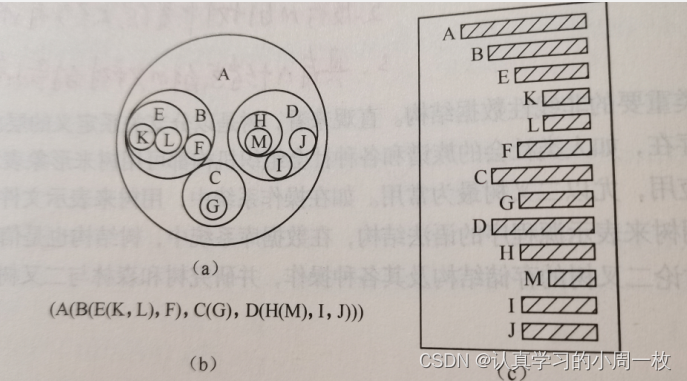
树的结构定义是一个递归的定义,即在树的定义中又用到树的定义,它道出了树的固有特性。树还可以有其他的表示形式,如图5.2所示为图5.1( b)中树的各种表示。其中( a)是以嵌套集合(即是一些集合的集体,对于其中任何两个集合,或者不相交,或者一个包含另一个)的形式表示的;(b)是以广义表的形式表示的,根作为由子树森林组成的表的名字写在表的左边;( c)用的是凹入表示法(类似书的编目)。表示方法的多样化,正说明了树结构在日常生活中及计算机程序设计中的重要性。一般来说,分等级的分类方案都可用层次结构来表示,也就是说,都可由一个树状结构来表示。
注意:
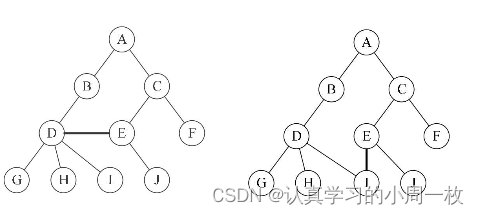
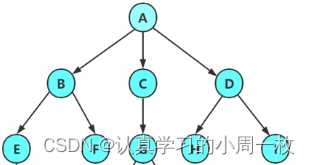
从其中我们还可以得出一个结论每个结点最多有一个父结点,需要注意的是虽然子树的个数没有限制,但是它们一定是互不交互的,下面的图明显不符合相应的原则,所以不是树
1.2树的结构
1.3树的相关概念
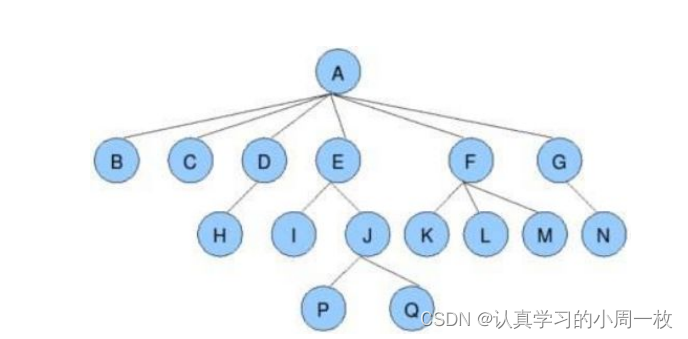
1.节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
2.叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I…等节点为叶节点
3.非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G…等节点为分支节点
4.双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
5.孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
6.兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
7.树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
8.节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
9.树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
10.堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
11.节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
12.子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
13.森林:由m(m>0)棵互不相交的树的集合称为森林;
1.4 树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的孩子兄弟表示法。
typedef int DataType;
struct Node
{struct Node* _firstChild1; // 第一个孩子结点struct Node* _pNextBrother; // 指向其下一个兄弟结点DataType _data; // 结点中的数据域
};
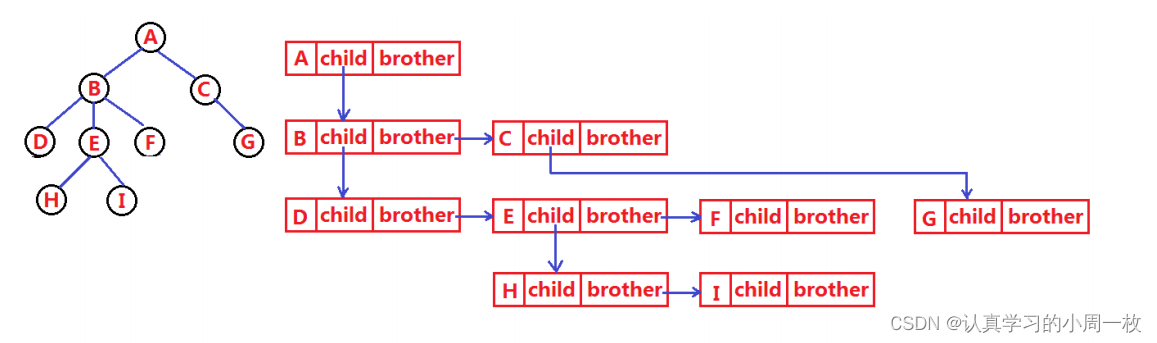
那么到底是如何实现的呢?我们通过下图来进行了解:
上图的链接过程可以通过以下展示出来:

解答:
开始时我们定义一个孩子指针和一个兄弟指针,第一步根结点的孩子指针指向根节点的第一个孩子,而根节点的其他孩子结点就根据第一个孩子结点的兄弟指针来进行链接操作,等兄弟指针指向空时即结束,以此类推后面。
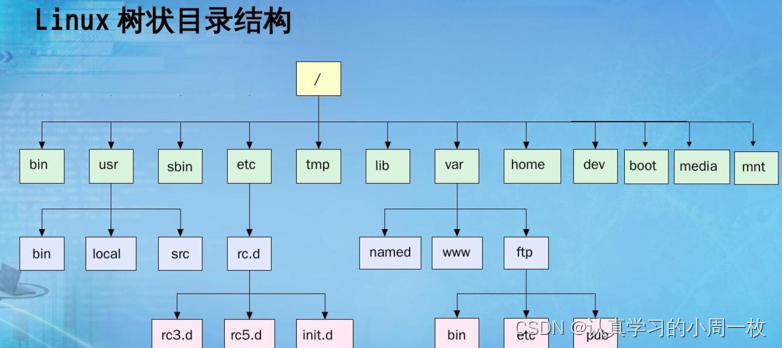
1.5 树在实际中的运用(表示文件系统的目录树结构)
2.二叉树概念及结构
2.1概念
二叉树是n(n>=0)个结点所构成的集合,它或为空树(n=0);或为非空树,对于非空树T:
(1)或者为空
(2) 由一个根节点加上两棵别称为左子树和右子树的二叉树组成
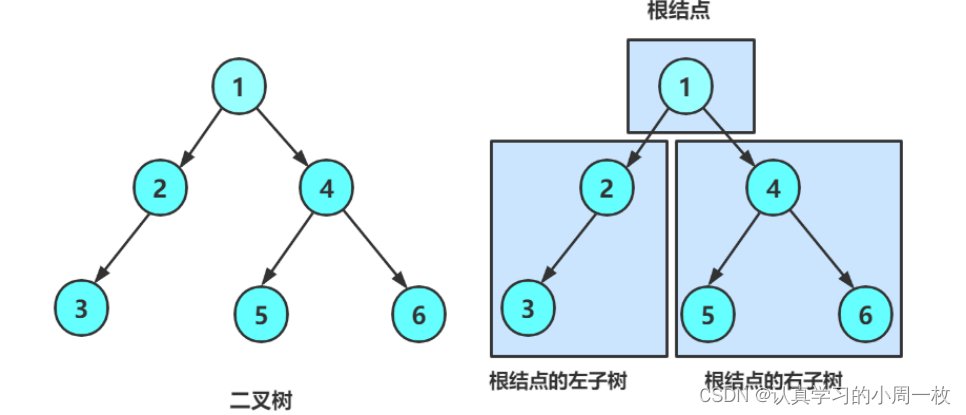
从上图可以看出:
- 二叉树不存在度大于2的结点
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
二叉树的递归定义表明二叉树或为空,或是由一个根结点加上两棵分别称为左子树和右子树的,互不相交的二叉树组成。由于这两棵子树也是二叉树,则由二叉树的定义,它们也可可以是空树。由此,二叉树可以有5种基本形态:
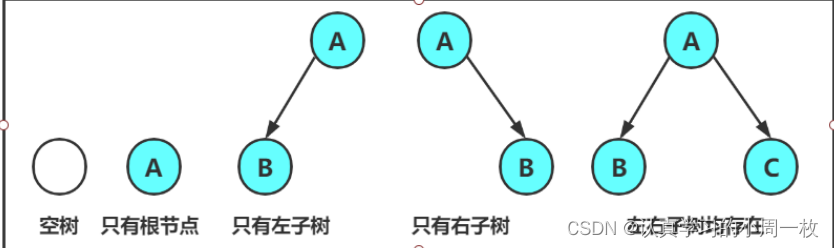
2.2现实中的二叉树

2.3 特殊的二叉树
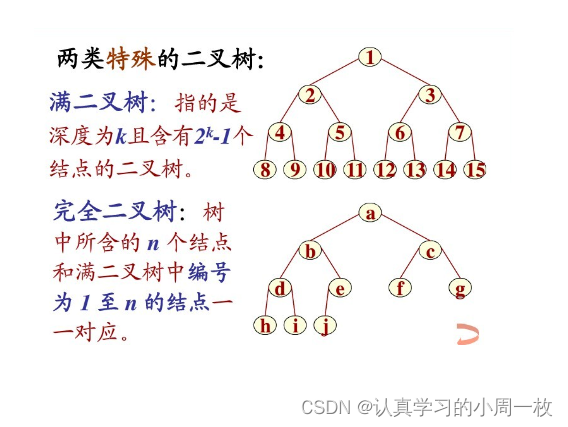
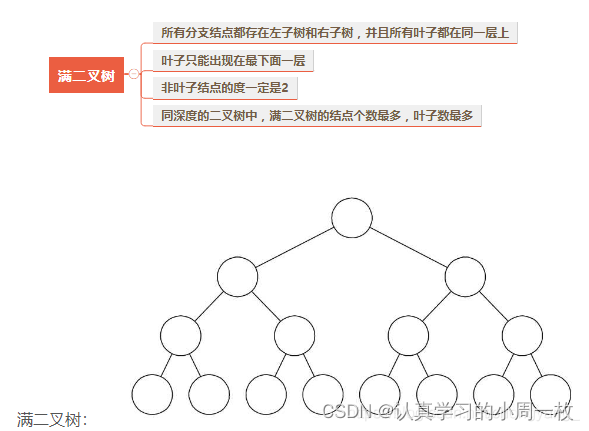
- 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是2的k次方减1 ,则它就是满二叉树。
- 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
2.4 二叉树的性质

性质1:在二叉树的第i层上至多有2i-1个结点(i>=1)
性质2:深度为k的二叉树至多有2k-1个结点(k>=1)
性质3:对任何一棵二叉树T,如果其终端结点数为n0,度为2的结点数为n2,则n0 = n2+1
一棵二叉树,除了终端结点(叶子结点),就是度为1或2的结点。假设n1表示度为1的结点数,则树 T 的结点总数n=n0+n1+n2,我们再换个角度,看一下树T的连接线数,除了根节点,其他结点都有一根线表示分支进入,所以连接线数为结点总数减去1。按连接线树算的话:n-1=n1+2n2,可推导出n0+n1+n2-1 = n1+2n2,继续推导可得n0 = n2+1
满二叉树:深度为 k 且含有 2k-1个结点
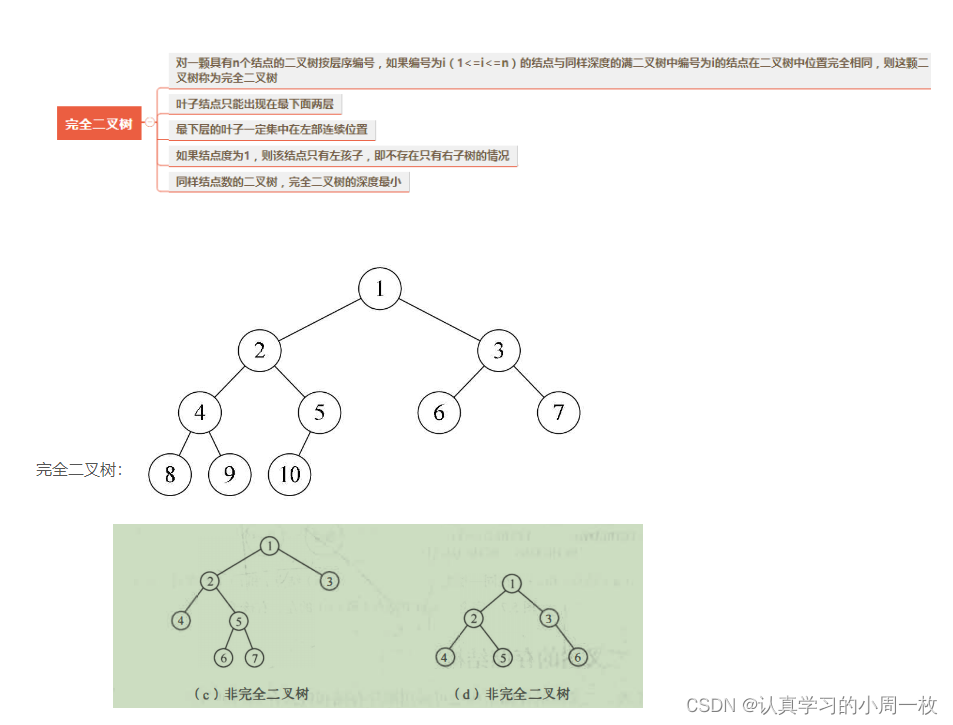
性质4:具有n个结点的完全二叉树的深度为[log2n ] + 1
性质5:如果对一颗有n个结点的完全二叉树(其深度为[log2n ] + 1)的结点按层序编号(从第1层到第[log2n ] + 1层,每层从左到右),对任一结点i(1<=i<=n)有:
1.如果i=1,则结点i是二叉树的根,无双亲;如果i>1,则其双亲是结点 [i/2]
2.如果2i>n,则结点 i 无孩子(结点i为叶子结点);否则其左孩子是结点 2i
3.如果2i+1>n,则结点 i 无右孩子;否则其右孩子是结点 2i+1
3.选择题
1.一棵完全二叉树共有 1001 个结点,则该二叉树中的叶子结点数为()
A.250
B.254
C.500
D.501
解答:
设二叉树中度为0的叶子结点个数为n0,度为1结点个数为n1,度为2结点个数为n2,于是n0 + n1 + n2 = 1001,根据二叉树性质:n0 = n 2 + 1,代入得到,2n2 + n1 = 1001 由于完全二叉树的n1 只能是0或者1,为满足2n2 + n1 = 1001,n1 = 1,因此n2 = 500 所以n0 = 501,即叶子个数是501个,所以选D
2.在具有 2n 个结点的完全二叉树中,叶子结点个数为()
A n
B n+1
C n-1
D n/2
解答:
完全二叉树是指除最后一层外,每一层上的结点数均达到最大值,在最后一层上只缺少右边的若干结点。根据完全二叉树性质,如果共 2n个结点,从根结点开始按层序用自然数 1 , 2 ,…, 2n 给结点编号,则编号为 n 的结点左子结点编号为 2n ,因此叶子结点编号为n+1,n+2, … ,2n 。故叶子结点个数为 n ,本题答案为 A 选项。
相关文章:

【树和二叉树】数据结构二叉树和树的概念认识
前言:在之前,我们已经把栈和队列的相关概念以及实现的方法进行了学习,今天我们将认识一个新的知识“树”!!! 目录1.树概念及结构1.1树的概念1.2树的结构1.3树的相关概念1.4 树的表示1.5 树在实际中的运用&a…...

通达信收费接口查询可申购新股c++源码分享
有很多股民在做股票交易时为了实现盈利会借助第三三方炒股工具帮助自己,那么通达信收费接口就是人们常用到的,今天小编来分享一下通达信收费接口查询可申购新股c源码: std::cout << " 查询可申购新股: category 12 \n"; c…...
。)
【C#设计模式】创建型设计模式 (单例,工厂)。
c# 创建型设计模式 1.单例设计模式c# 单例JS 单例(ES6)c# 扩展方法c# 如果窗体非单例(tips:窗口可以容器化)2.工厂设计模式JS 简单工厂(ES6)C# 简单工厂C# params关键词(自定义参数个数)JS 手写JQuery(委托,工厂方式隐藏细节)JS ...四种用法C# 偷懒工厂1.单例设计模式 …...
Ubuntu 22.04 LTS 入门安装配置优化、开发软件安装一条龙
Ubuntu 22.04 LTS 入门安装配置&优化、开发软件安装 例行前言 最近在抉择手上空余的笔记本(X220 i7-2620M,Sk Hynix ddr3 8G*2 ,Samsung MINISATA 256G)拿来运行什么系统比较好,早年间我或许还会去继续使用Win…...
第五十章 动态规划——数位DP模型
第五十章 动态规划——数位DP模型一、什么是数位DP数位DP的识别数位DP的思路二、例题1、AcWing 1083. Windy数(数位DP)2、AcWing 1082. 数字游戏(数位DP)3、AcWing 1081. 度的数量(数位DP)一、什么是数位DP…...
02- pandas 数据库 (机器学习)
pandas 数据库重点: pandas 的主要数据结构: Series (一维数据)与 DataFrame (二维数据)。 pd.DataFrame(data np.random.randint(0,151,size (5,3)), # 生成pandas数据 index [Danial,Brandon,softpo,Ella,Cindy], # 行索引 …...

学Qt想系统的学习,看哪本书?
Qt 是一个跨平台应用开发框架(framework),它是用 C语言写的一套类库。使用 Qt 能为 桌面计算机、服务器、移动设备甚至单片机开发各种应用(application),特别是图形用户界面 (graphical user in…...
)
2023年网络安全比赛--跨站脚本攻击②中职组(超详细)
一、竞赛时间 180分钟 共计3小时 二、竞赛阶段 1.访问服务器网站目录1,根据页面信息完成条件,将获取到弹框信息作为flag提交; 2.访问服务器网站目录2,根据页面信息完成条件,将获取到弹框信息作为flag提交; 3.访问服务器网站目录3,根据页面信息完成条件,将获取到弹框信息…...

网络安全实验室4.注入关
4.注入关 1.最简单的SQL注入 url:http://lab1.xseclab.com/sqli2_3265b4852c13383560327d1c31550b60/index.php 查看源代码,登录名为admin 最简单的SQL注入,登录名写入一个常规的注入语句: admin’ or ‘1’1 密码随便填,验证…...

领域搜索算法之经典The Lin-Kernighan algorithm
领域搜索算法之经典The Lin-Kernighan algorithmThe Lin-Kernighan algorithm关于算法性能提升的约束参考文献领域搜索算法是TSP问题中的三大经典搜索算法之一,另外两种分别是回路构造算法和组合算法。 而这篇文章要介绍的The Lin-Kernighan algorithm属于领域搜索算…...

深度学习基础-机器学习基本原理
本文大部分内容参考《深度学习》书籍,从中抽取重要的知识点,并对部分概念和原理加以自己的总结,适合当作原书的补充资料阅读,也可当作快速阅览机器学习原理基础知识的参考资料。 前言 深度学习是机器学习的一个特定分支。我们要想…...

C语言操作符详解 一针见血!
目录算数操作符移位操作符位操作符赋值操作符单目操作符关系操作符逻辑操作符条件操作符逗号表达式下标引用、函数调用和结构成员表达式求值11.1 隐式类型转换算数操作符💭 注意/ 除法 --得到的是商% 取模(取余)--得到的是余数如果除法操作符…...
前端面试题汇总
一:JavaScript 1、闭包是什么?利弊?如何解决弊端? 闭包是什么:JS中内层函数可以访问外层函数的变量,外层函数无法操作内存函数的变量的特性。我们把这个特性称作闭包。 闭包的好处: 隔离作用…...

以数据驱动管理场景,低代码助力转型下一站
数据驱动 数据驱动,是通过移动互联网或者其他的相关软件为手段采集海量的数据,将数据进行组织形成信息,之后对相关的信息讲行整合和提炼,在数据的基础上经过训练和拟合形成自动化的决策模型,简单来说,就是…...

2023年全国数据治理DAMA-CDGA/CDGP考试报名到弘博创新
弘博创新是DAMA中国授权的数据治理人才培养基地,贴合市场需求定制教学体系,采用行业资深名师授课,理论与实践案例相结合,快速全面提升个人/企业数据治理专业知识与实践经验,通过考试还能获得数据专业领域证书。 DAMA认…...

流程控制之循环
文章目录五、流程控制之循环5.1 步进循环语句for5.1.1 带列表的for循环语句5.1.2 不带列表的for循环语句5.1.3 类C风格的for循环语句5.2 while循环语句5.2.1 while循环读取文件5.2.2 while循环语句示例5.3 until循环语句5.4 select循环语句5.5 嵌套循环5.4 利用break和continue…...
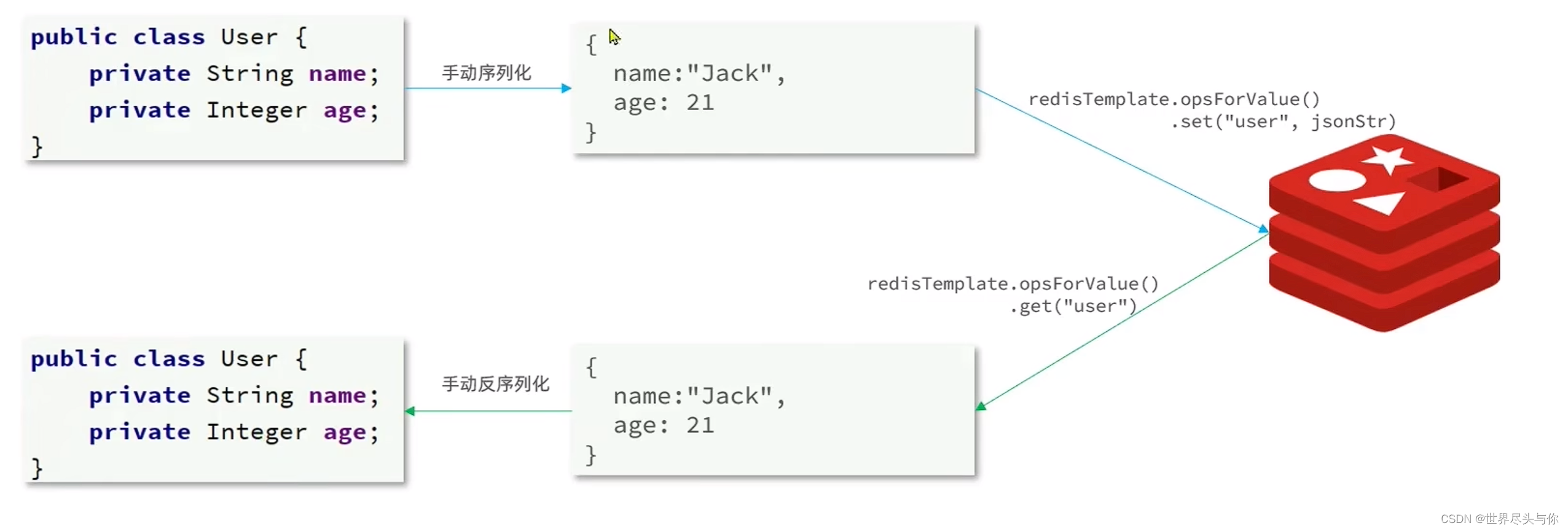
SpringDataRedis快速入门
SpringDataRedis快速入门1.SpringDataRedis简介2.RedisTemplate快速入门3.RedisSerializer4.StringRedisTemplate1.SpringDataRedis简介 SpringData是Spring中数据操作的模块,包含对各种数据库的集成,其中对Redis的集成模块就叫做SpringDataRedis Spri…...

MySQL 的执行计划 explain 详解
目录 什么是执行计划 执行计划的内容 select子句的类型 访问类型 索引的存在形式...
2023年网络安全比赛--Web综合渗透测试中职组(超详细)
一、竞赛时间 180分钟 共计3小时 二、竞赛阶段 1.通过URL访问http://靶机IP/1,对该页面进行渗透测试,将完成后返回的结果内容作为FLAG值提交; 2.通过URL访问http://靶机IP/2,对该页面进行渗透测试,将完成后返回的结果内容作为FLAG值提交; 3.通过URL访问http://靶机IP/3,对…...
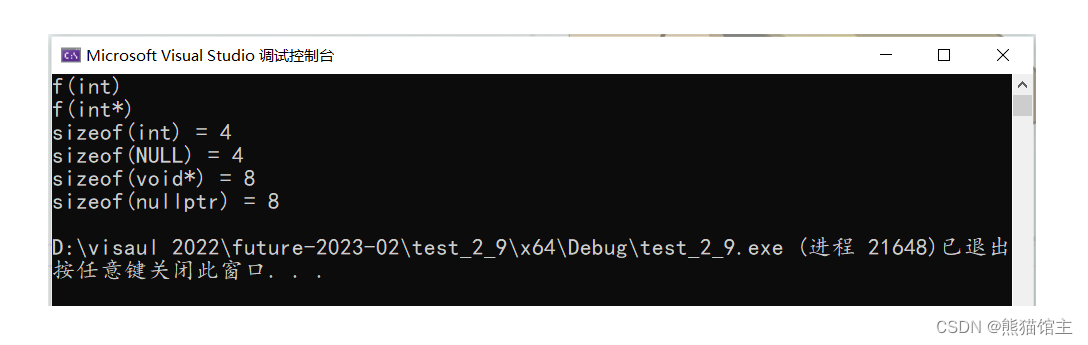
【c++之于c的优化 - 下】
前言 一、inline 概念 以inline修饰的函数叫做内联函数,编译时C编译器会在调用内联函数的地方展开,没有函数调用建立栈帧的开销,内联函数提升程序运行的效率。 如果在上述函数前增加inline关键字将其改成内联函数,在编译期间编译…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

MeshGPT 笔记
[2311.15475] MeshGPT: Generating Triangle Meshes with Decoder-Only Transformers https://library.scholarcy.com/try 真正意义上的AI生成三维模型MESHGPT来袭!_哔哩哔哩_bilibili GitHub - lucidrains/meshgpt-pytorch: Implementation of MeshGPT, SOTA Me…...

C# WPF 左右布局实现学习笔记(1)
开发流程视频: https://www.youtube.com/watch?vCkHyDYeImjY&ab_channelC%23DesignPro Git源码: GitHub - CSharpDesignPro/Page-Navigation-using-MVVM: WPF - Page Navigation using MVVM 1. 新建工程 新建WPF应用(.NET Framework) 2.…...
LeetCode - 148. 排序链表
目录 题目 思路 基本情况检查 复杂度分析 执行示例 读者可能出的错误 正确的写法 题目 148. 排序链表 - 力扣(LeetCode) 思路 链表归并排序采用"分治"的策略,主要分为三个步骤: 分割:将链表从中间…...

开源 vGPU 方案:HAMi,实现细粒度 GPU 切分
本文主要分享一个开源的 GPU 虚拟化方案:HAMi,包括如何安装、配置以及使用。 相比于上一篇分享的 TimeSlicing 方案,HAMi 除了 GPU 共享之外还可以实现 GPU core、memory 得限制,保证共享同一 GPU 的各个 Pod 都能拿到足够的资源。…...

分布式计算框架学习笔记
一、🌐 为什么需要分布式计算框架? 资源受限:单台机器 CPU/GPU 内存有限。 任务复杂:模型训练、数据处理、仿真并发等任务耗时严重。 并行优化:通过任务拆分和并行执行提升效率。 可扩展部署:适配从本地…...