40.利用欧拉法求解微分方程组(matlab程序)
1.简述
求解微分方程的时候,如果不能将求出结果的表达式,则可以对利用数值积分对微分方程求解,获取数值解。欧拉方法是最简单的一种数值解法。前面介绍过MATLAB实例讲解欧拉法求解微分方程,今天实例讲解欧拉法求解一阶微分方程组。
本文理论部分来自知乎作者云端之下的文章“常微分方程——数值解——欧拉方法”
微分方程的求解方法有解析解法和数值解法,解析法是求出因变量关于时间 �的具体函数式,表达 ;数值法是解出因变量 关于时间 �的离散序列,通常表达离散数据对。绝大多数的非线性常微分方程,不存在或难以求出解析解,大多数情况下只能求取微分方程的数值解。
2.代码
%% 学习目标:欧拉法求解微分方程组
clear;clc
c=2/3; %设置c的值
x(1)=0.1; %设置x初值为0.1
y(1)=0.3; %设置y初值为0.3
h=0.05; %设置步长为0.05
%for循环:根据Euler法,求解微分方程组
for i=1:1000
x(i+1)=x(i)+h*(x(i)*(c-x(i)/y(i)));
y(i+1)=y(i)+h*(y(i)*(1-y(i))-x(i)*y(i));
end
t=0:h:1000*h; %计算时间
plot(t,x) %绘制x曲线
hold on
plot(t,y,'r') %绘制y曲线
xlabel('time') %设置x轴的标签
ylabel('value') %设置y轴的标签
legend({'x','y'}) %设置图例
title('time evolution plot') %设置图形的标题
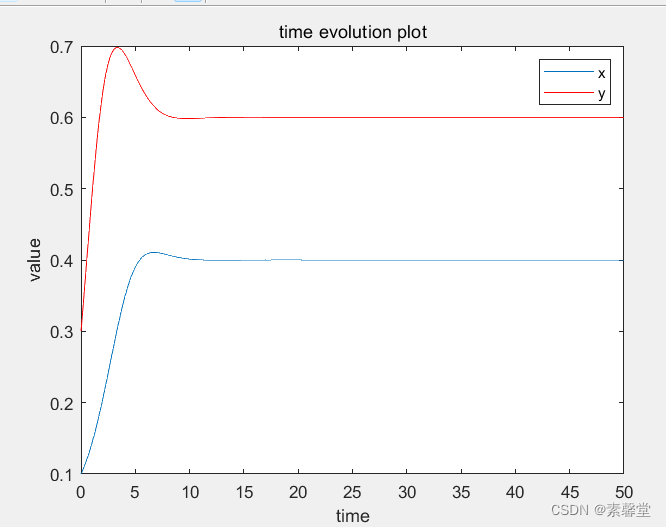
figure
plot(x,y) %绘制phase图
title('phase plane plot') %设置标题
xlabel('x') %设置x轴的标签
ylabel('y') %设置y轴的标签
3.运行结果

相关文章:

40.利用欧拉法求解微分方程组(matlab程序)
1.简述 求解微分方程的时候,如果不能将求出结果的表达式,则可以对利用数值积分对微分方程求解,获取数值解。欧拉方法是最简单的一种数值解法。前面介绍过MATLAB实例讲解欧拉法求解微分方程,今天实例讲解欧拉法求解一阶微分方程组。…...

OpenAI-Translator 实战总结
最近在极客时间学习《AI 大模型应用开发实战营》,自己一边跟着学一边开发了一个进阶版本的 OpenAI-Translator,在这里简单记录下开发过程和心得体会,供有兴趣的同学参考 功能概览 通过openai的chat API,实现一个pdf翻译器实现一个…...
【工业机器人】用于轨迹规划和执行器分析的机械手和移动机器人模型(MatlabSimulink)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

开源在线文档服务OnlyOffice
开源在线文档服务OnlyOffice应用启动与示例运行 - 掘金 ONLYOFFICE API 文档 - Example - IDEA运行Java示例 | ONLYOFFICE中文网 NEXTCLOUDonlyoffice的搭建和使用_nextcloud onlyoffice_莫冲的博客-CSDN博客 OnlyOffice java 部署使用,文件流方式 预览文件 | 言曌博…...

汽车基本常识
目录 电源KL30KL15 零部件简称 电源 KL30 KL15 零部件简称 VCU:整车控制器 直接网络管理节点 CDU:充电系统控制器 MCU:电机控制器 TCU:变速箱控制器 ABS:防抱死系统 EPS:助力转向 T-Box:远程…...

百度资深PMO阚洁受邀为第十二届中国PMO大会演讲嘉宾
百度在线网络技术(北京)有限公司资深PMO阚洁女士受邀为由PMO评论主办的2023第十二届中国PMO大会演讲嘉宾,演讲议题:运筹于股掌之间,决胜于千里之外 —— 360斡旋项目干系人。大会将于8月12-13日在北京举办,…...

为什么C++有多种整型?
C中有多种整型是为了满足不同的需求,提供更灵活和高效的整数表示方式。不同的整型具有不同的字节大小、范围和精度,可以根据应用的需求选择合适的整型类型。以下是一些原因解释为什么C有多种整型: 内存和性能优化:不同的整型在内存…...
玩一玩通义千问Qwen开源版,Win11 RTX3060本地安装记录!
大概在两天前,阿里做了一件大事儿。 就是开源了一个低配版的通义千问模型--通义千问-7B-Chat。 这应该是国内第一个大厂开源的大语言模型吧。 虽然是低配版,但是在各类测试里面都非常能打。 官方介绍: Qwen-7B是基于Transformer的大语言模…...

oracle积累增量和差异增量
积累增量和差异增量: 对于 RMAN 来说,积累增量备份和差异增量备份都是增量备份的一种形式,它们之间的区别在于备份的范围和备份集的方式。 积累增量备份:在进行积累增量备份时,RMAN 会备份自最后一次完全备份或增量备…...
利用C++nlohmann库解析json文件
json文件示例: 代码运行环境VS2019 一、git下载nlohmann库文件源代码 源代码文件目录 二、利用VS2019新建工程,并配置项目属性 配置VC目录---包含目录 三、项目源代码 #include <iostream> #include <fstream> #include <nlohmann/jso…...

OpenCV 中的光流 (C++/Python)
什么是光流? 光流是一项视频中两个连续帧之间每像素运动估计的任务。基本上,光流任务意味着计算像素的位移矢量作为两个相邻图像之间的对象位移差。光流的主要思想是估计物体由其运动或相机运动引起的位移矢量。 理论基础 假设我们有一个灰度图像——具有像素强度的矩阵。我…...
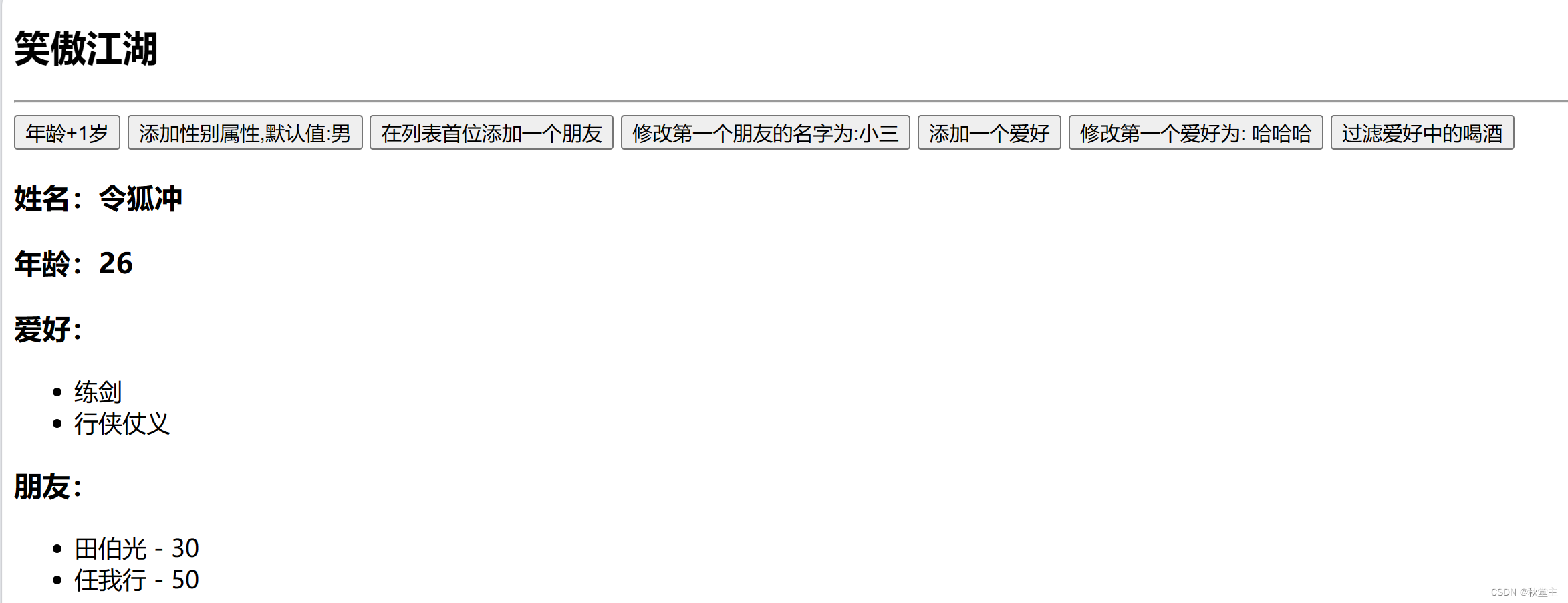
第9集丨Vue 江湖 —— 监测数据原理
目录 一、修改数据时的一个问题1.1 现象一1.2 现象二 二、Vue监测数据原理2.1 模拟一个数据监测2.2 数据劫持2.3 Vue.set()/vm.$set()2.4 基本原理2.4.1 如何监测对象中的数据?2.4.2 如何监测数组中的数据?2.4.3 修改数组中的某个元素 2.5 案例2.5.1 需求功能2.5.2 实现 一、…...

【YOLO】替换骨干网络为轻量级网络MobileNet3
替换骨干网络为轻量级网络MobileNet_v3 上一章 模型网络结构解析&增加小目标检测 文章目录 替换骨干网络为轻量级网络MobileNet_v3前言一、MobileNetV3介绍二、MobileNetV2&MobileNetV3三、MobileNetV3网络结构1. 结构查看2. 查看每层featuremap大小三、YOLOV5替换骨干…...
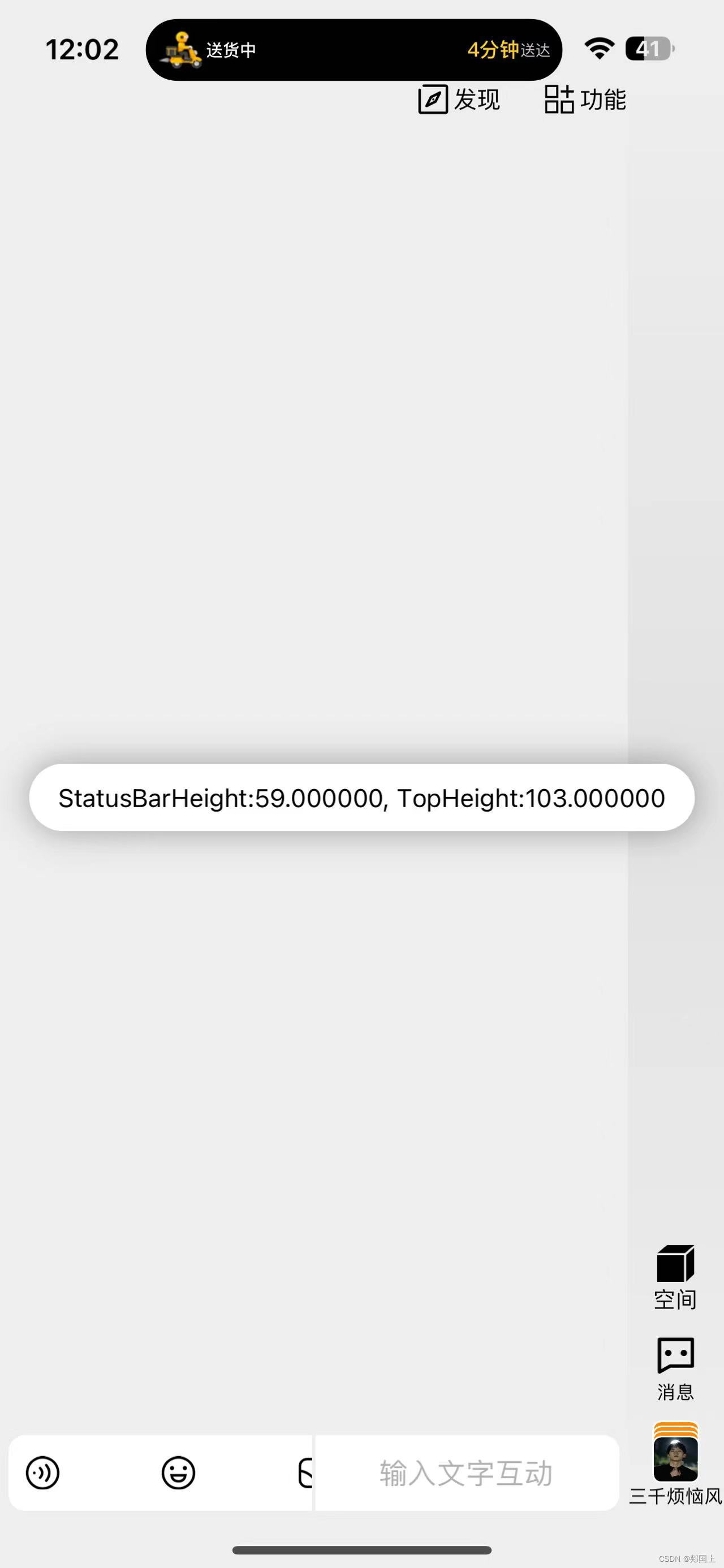
如何识别手机是否有灵动岛(dynamic island)
如何识别手机是否有灵动岛(dynamic island) 灵动岛是苹果2022年9月推出的iPhone 14 Pro、iPhone 14 Pro Max首次出现,操作系统最低是iOS16.0。带灵动岛的手机在竖屏时顶部工具栏大于等于51像素。 #define isHaveDynamicIsland ({ BOOL isH…...

Linux设备树简介
一、起源 减少垃圾代码 减轻驱动开发工作量 驱动代码和设备信息分离 参考Open Fireware设计 用来记录硬件平台中各种硬件设备的属性信息 二、基本组成 两种源文件: xxxxx.dts dts是device tree source的缩写 xxxxx.dtsi dtsi是device tree source include的…...

Ubuntu类IOS主题设置
1.依次执行下面三条命令: sudo apt install gnome-shell-extensions sudo apt install gnome-tweak-tool sudo apt install chrome-gnome-shell2.下载主题,也是命令: git clone <https://github.com/qingchendelaike/GNOME-OSX-II-Theme…...
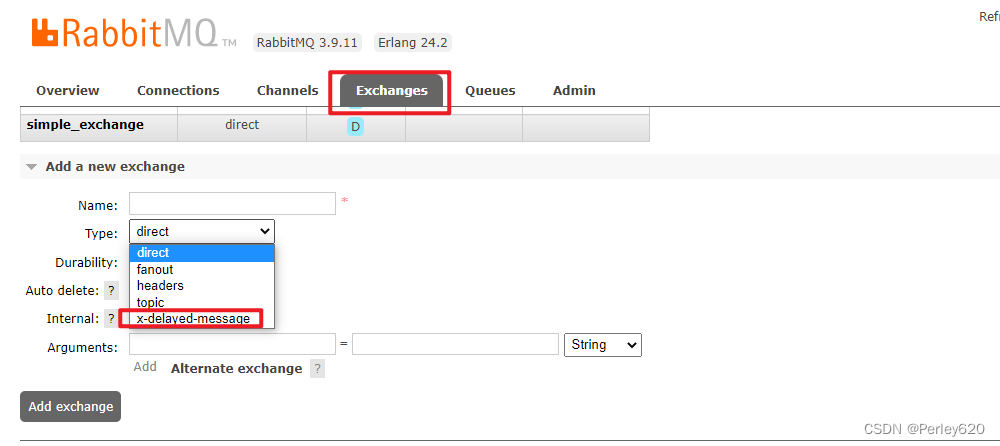
RabbitMQ学习——发布订阅/fanout模式 topic模式 rabbitmq回调确认 延迟队列(死信)设计
目录 引出点对点(simple)Work queues 一对多发布订阅/fanout模式以登陆验证码为例pom文件导包application.yml文件rabbitmq的配置生产者生成验证码,发送给交换机消费者消费验证码 topic模式配置类增加配置生产者发送信息进行发送控制台查看 rabbitmq回调确认配置类验…...
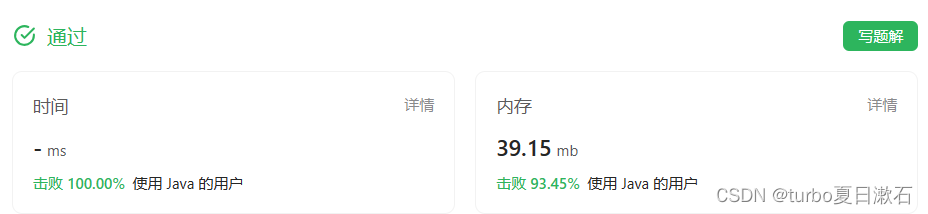
Leetcode算法递归类—合并两个有序链表
目录 21. 合并两个有序链表 题解: 代码: 将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 示例 1: 输入:l1 [1,2,4], l2 [1,3,4] 输出:[1,1,2,3,4,4]示例 2&a…...
YOLOv5可视化界面
Pyside6可视化界面 安装Pyside6 激活之前的虚拟环境yolov5 在该环境的终端输入以下命令 pip install -i https://pypi.tuna.tsinghua.edu.cn/simple pyside6输入where python找到当前使用的Python的路径 找到该路径下的designer.exe文件(/Lib/site-packages/PySi…...

C语言使用库函数实现大小写字母转换
功能;多行输入,输入大写字母,返回相应的小写字母;输入小写字母,返回相应的大写字母 需要用到的库函数: islower() -- 判断是否为小写,是,返回非0,…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...
