解析湖仓一体的支撑技术及实践路径
自2021年“湖仓一体”首次写入Gartner数据管理领域成熟度模型报告以来,随着企业数字化转型的不断深入,“湖仓一体”作为新型的技术受到了前所未有的关注,越来越多的企业视“湖仓一体” 为数字化转型的重要基础设施。
01
数据平台的发展历程
需求催生技术革新,在存储海量数据需求的推动下,数据平台架构持续演进,经过数十年的发展,主要经历了数据库、数据仓库、数据湖三个阶段。湖仓一体是数据平台发展的重要趋势。

第一阶段:数据库
诞生于20世纪60年代,主要用于OLTP场景。代表产品: Oracle、SQL Server、Mysql等
第二阶段:数据仓库
20世纪90年代代数据仓库理论被提出,主要用OLAP场景分析。传统数仓有Clickhouse、Greenplum等,云数仓有AWS redshift、Snowflake等。
第三阶段:数据湖
2010年数据湖概念被提出,随着三大开源数据湖技术的成熟,数据湖产品加速落地。代表产品有亚马逊-S3、LakeForation,阿里云-数据湖构建DLF、数据开发治理Dataworks、对象存储OSS、开源大数据平台EMR等。
02
数据湖、数据仓库特性分析
数据仓库主要用于解决单个关系型数据库架构,无法支撑庞大数据量的数据存储问题,很好地解决了TB到PB级别的数据处理问题,但是由于数据仓库仍以结构化数据为主,无法解决业务增长带来的半结构化、非结构化数据的存储、处理问题,且其整个建设过程需要遵循一系列规范,比如标准化的数据集成模式和存储格式、统一的数据仓库分层分域模型以及指标体系建设等,带来了数据仓库建设存储成本高、维护开发难度大、扩展能力受限制等问题。
数据湖的出现很好解决了数据仓库建设存在的一系列问题,将数据管理的流程简化为数据入湖和数据分析两个阶段。数据湖支持各种 类型数据的统一存储。数据分析则以读取型(schema on read)形式,极大提升分析效率。然而数据湖对多样类型数据的支持以及灵活高效的 分析方式,带来了数据治理难的问题,比如因为缺乏治理导致数据质量下降、数据不可用等,很容易退化形成数据沼泽。
结论:数据仓库和数据湖是两套相对独立的体系,各有优劣势,无法相互替代。

△数据湖与数据仓库对比表
03
湖+仓混合业务架构
为满足存储多种数据类型、多场景分析等业务诉求,企业采用混合部署模式,数据湖、数据仓库、关系型数据库等多种架构并存,其中数据湖和数据仓库通过ETL进行数据交换。
数据湖和数据仓库是两套独立的体系,其中数据湖基于 Hadoop 技术生态 (HDFS、Spark、Flink 等技术)来实现,主要用于支撑多源异构的数 据存储,执行批处理、流处理等工作负载。数据仓库主要基于 MPP 或 者关系型数据库来实现,主要支撑结构化数据在 OLAP 场景下的 BI 分析和查询需求。
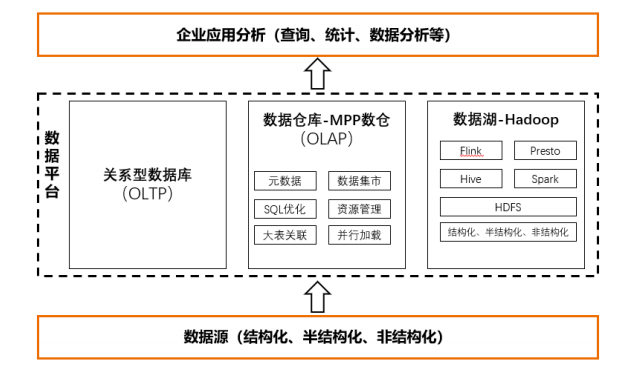
△湖+仓混合架构图
“数据湖+数据仓库”混合架构满足了结构化、半结构化、非结构化数据高效处理需求,解决了传统数据仓库在海量数据下加载慢、数据查询效率低、难以融合多种异构数据源进行分析的问题,但也存在明显的四大弊端。一是数据冗余,增加存储成本。二是两个系统间额外的 ETL(抽取、转化、加载)流程导致时效性差。三是数据一致性保障低,增加数据校验成本。四是混合架构复杂,开发运维难度大、成本高。
04
湖仓一体实践路径
“数据湖+数据仓库”混合架构是技术向业务妥协的一个产物,并不是真正意义的湖仓一体平台。2020年Databrics提出“湖仓一休”概念。湖仓一体是指融合数据湖与数据仓库的优势,形成一体化、开放 式数据处理平台的技术。通过湖仓一体技术,可使得数据处理平台底 层支持多数据类型统一存储,实现数据在数据湖、数据仓库之间无缝 调度和管理,并使得上层通过统一接口进行访问查询和分析。具备的能力包括:
-
多模存储:多样数据统一存储
-
架构统一:统一资源调度、存储管理、计算引擎、查询接口
-
性能优越:数据加工链路缩短资源复用性增加、时效性提高
-
场景多元:多样化业务场景和极致用户体验

△湖仓一体架构技术架构图
总体来看,湖仓一体通过引入数据仓库治理能力,既可以很好地解决数据湖建设的数据治理难问题,也能更好地挖掘数据湖中的数据价值,将高效建仓和灵活建湖两大优势融合在一起,提升了数据管理效率和灵活性。
企业需求的驱动下,数据湖与数据仓库在原本的范式之上向其限制范用扩展,逐渐形成了“湖上建仓”与“仓外挂湖”两种湖仓一体实现路径。湖上建仓和仓外挂湖虽然出发点不同,但最终湖仓一体的目标标一致。

△两种实现路径对比表
湖上建仓
定义:是指基于云存储或第三方对象存储的云数据湖架构,或者基于开源 Hadoop 生态体系并以 DeltaLake、Hudi、Iceberg 三大开 源数据湖作为数据存储中间层实现多源异构数据的统一存储,以统一调用接口方式调用计算引擎,最终实现上下结构的湖仓一体架构。
原理:以数据湖为基石,在数据湖中引入数据仓库的数据治理能力,实现数据湖到湖仓一体的进化。
实现方案:基于云存储或第三方对象存储的云数据湖架构,基于开源Hadoop生态体系扩展。
仓外挂湖
定义:是指以 MPP 数据库为基础,使用可插拔架构,通过开放接口对接外部存储实现统一存储,在存储底层共享一份数据,计算、 存储完全分离,实现从强管理到兼容开放存储和多引擎。
原理:以MPP数据库为核心,使用可插拔架构,通过开放接口对接外部存储实现统一存储。
实现方案:基于云原生MPP数据库构建。
05
亿信华辰湖仓一体解决方案
湖仓一体的核心是实现数据湖和数据仓库中的数据、元数据的无缝打通,并可自由流动。亿信华辰结合多年的BI和数仓实施经验,综合传统数据仓库和现代数据湖两种技术特点,推出了仓湖一体解决方案。该建设方案涵盖数据存储、数据集成、数据交换、数据共享等多个方面,综合数据湖、数据仓库两种技术演进方向,为企业用户提供云原生仓湖一体解决方案,构建企业数字化新基座。
亿信华辰仓湖一体数据中心定位于为企业提供易于部署、开发、运维的数据底座平台,平台提供的能力包括:数据的统一分类存储,数据采集加工的流程自动化,可视化的数据开发,提供多样化的数据共享访问标准接口等等。建设内容包括数据采集、数据处理、数据建模、数据交换四大方面。
湖仓一体行业正处在发展初期,总的来看湖仓一体并不是一个纯技术攻关工作,而是技术逐步融合、整合的过程,其本质是异构数据平台走向一体化的过渡阶段。亿信华辰基于客户需求和技术演进趋势持续创新,为企业客户提供仓湖一体解决方案,致力于构建企业数据资源共享池,让企业业务的创新更敏捷,业务洞察更准确,加速释放数据价值。
以上部分内容引用CCSA TC601《湖仓一体技术与产业研究报告》
相关文章:
解析湖仓一体的支撑技术及实践路径
自2021年“湖仓一体”首次写入Gartner数据管理领域成熟度模型报告以来,随着企业数字化转型的不断深入,“湖仓一体”作为新型的技术受到了前所未有的关注,越来越多的企业视“湖仓一体” 为数字化转型的重要基础设施。 01 数据平台的发展历程…...
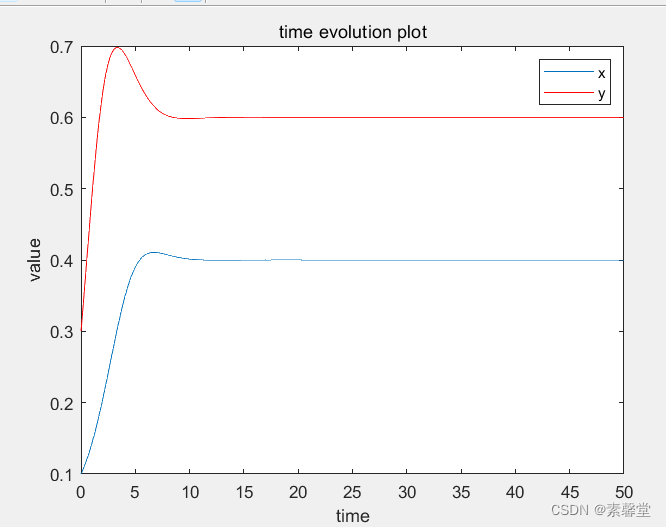
40.利用欧拉法求解微分方程组(matlab程序)
1.简述 求解微分方程的时候,如果不能将求出结果的表达式,则可以对利用数值积分对微分方程求解,获取数值解。欧拉方法是最简单的一种数值解法。前面介绍过MATLAB实例讲解欧拉法求解微分方程,今天实例讲解欧拉法求解一阶微分方程组。…...

OpenAI-Translator 实战总结
最近在极客时间学习《AI 大模型应用开发实战营》,自己一边跟着学一边开发了一个进阶版本的 OpenAI-Translator,在这里简单记录下开发过程和心得体会,供有兴趣的同学参考 功能概览 通过openai的chat API,实现一个pdf翻译器实现一个…...
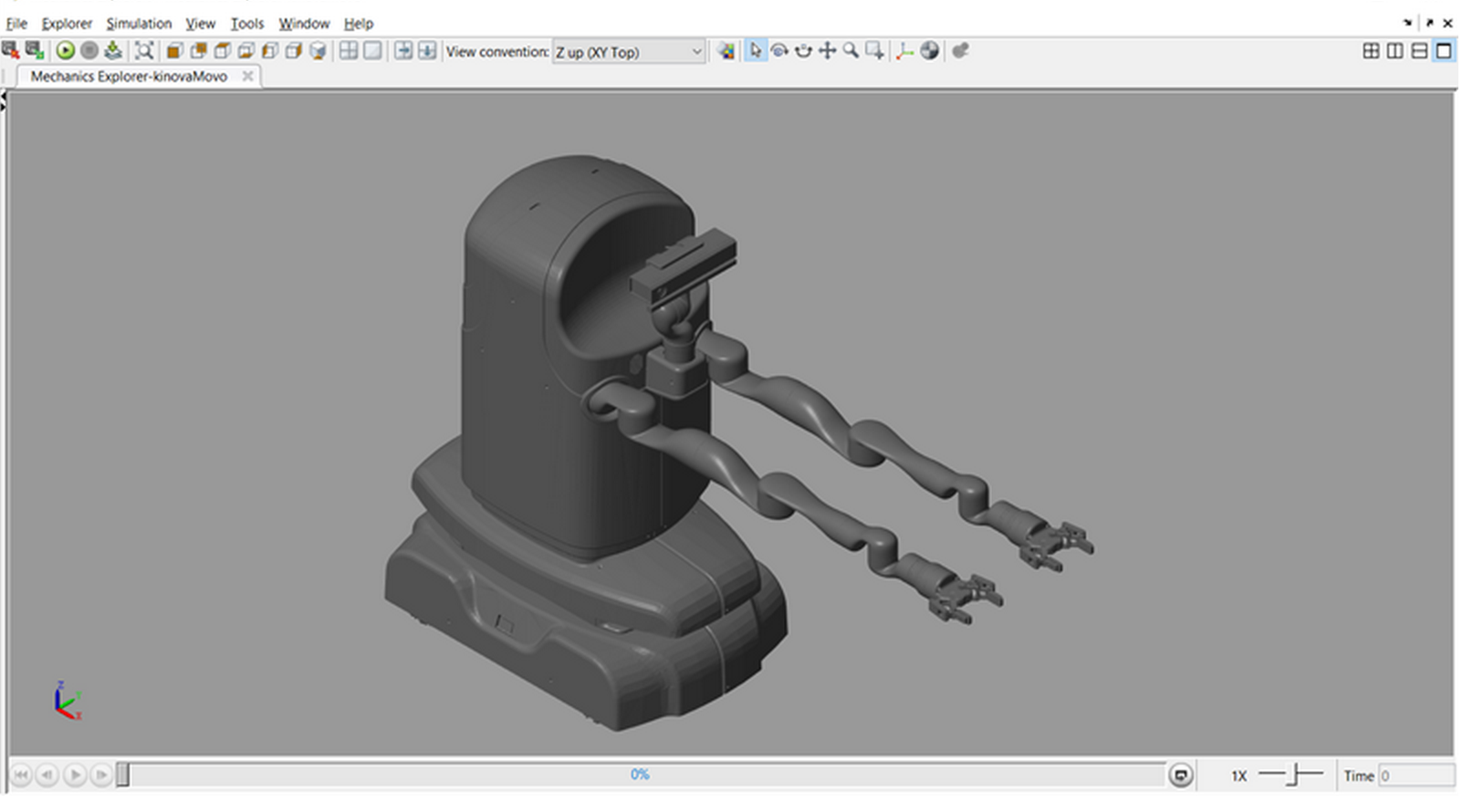
【工业机器人】用于轨迹规划和执行器分析的机械手和移动机器人模型(MatlabSimulink)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

开源在线文档服务OnlyOffice
开源在线文档服务OnlyOffice应用启动与示例运行 - 掘金 ONLYOFFICE API 文档 - Example - IDEA运行Java示例 | ONLYOFFICE中文网 NEXTCLOUDonlyoffice的搭建和使用_nextcloud onlyoffice_莫冲的博客-CSDN博客 OnlyOffice java 部署使用,文件流方式 预览文件 | 言曌博…...

汽车基本常识
目录 电源KL30KL15 零部件简称 电源 KL30 KL15 零部件简称 VCU:整车控制器 直接网络管理节点 CDU:充电系统控制器 MCU:电机控制器 TCU:变速箱控制器 ABS:防抱死系统 EPS:助力转向 T-Box:远程…...

百度资深PMO阚洁受邀为第十二届中国PMO大会演讲嘉宾
百度在线网络技术(北京)有限公司资深PMO阚洁女士受邀为由PMO评论主办的2023第十二届中国PMO大会演讲嘉宾,演讲议题:运筹于股掌之间,决胜于千里之外 —— 360斡旋项目干系人。大会将于8月12-13日在北京举办,…...

为什么C++有多种整型?
C中有多种整型是为了满足不同的需求,提供更灵活和高效的整数表示方式。不同的整型具有不同的字节大小、范围和精度,可以根据应用的需求选择合适的整型类型。以下是一些原因解释为什么C有多种整型: 内存和性能优化:不同的整型在内存…...
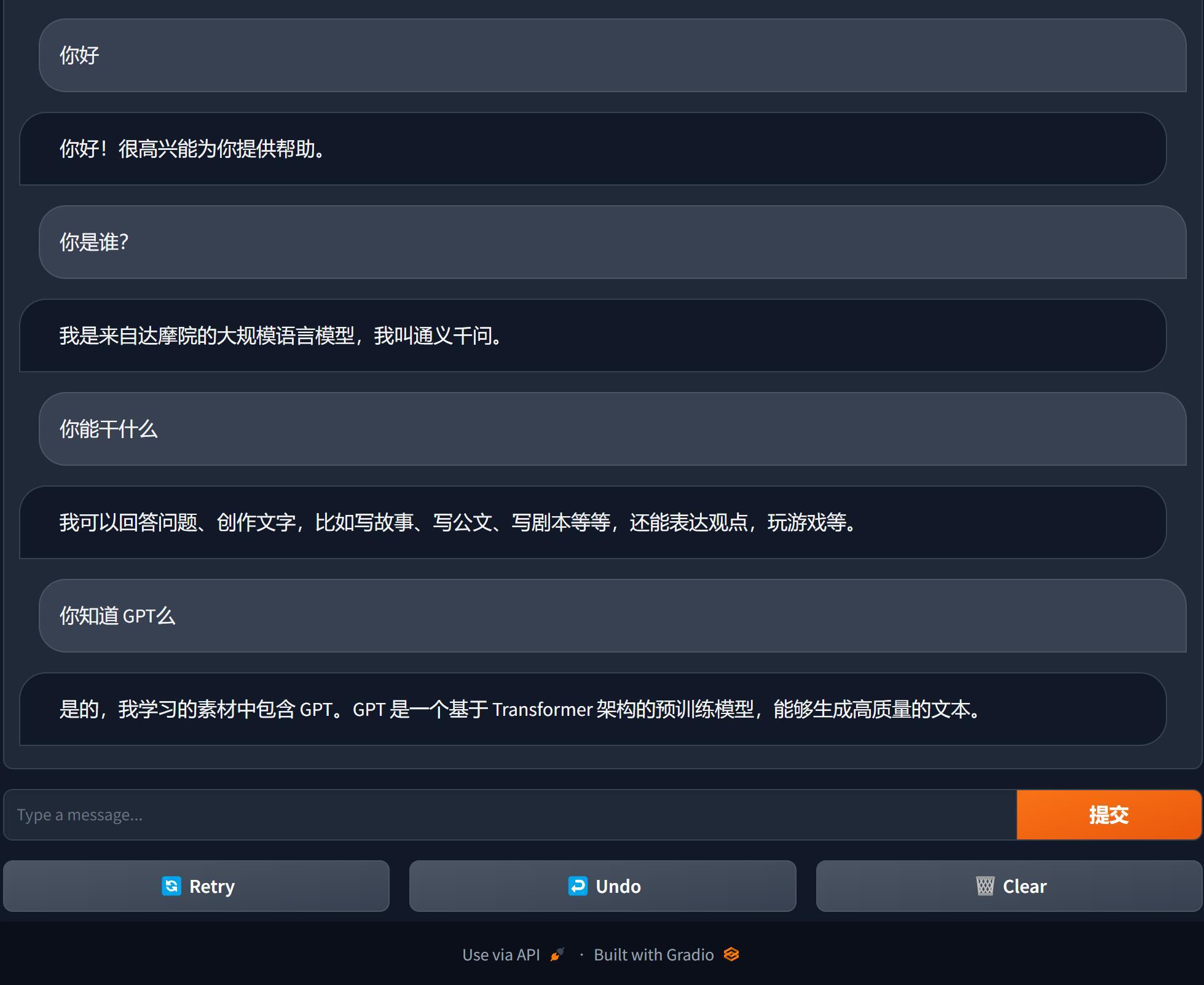
玩一玩通义千问Qwen开源版,Win11 RTX3060本地安装记录!
大概在两天前,阿里做了一件大事儿。 就是开源了一个低配版的通义千问模型--通义千问-7B-Chat。 这应该是国内第一个大厂开源的大语言模型吧。 虽然是低配版,但是在各类测试里面都非常能打。 官方介绍: Qwen-7B是基于Transformer的大语言模…...

oracle积累增量和差异增量
积累增量和差异增量: 对于 RMAN 来说,积累增量备份和差异增量备份都是增量备份的一种形式,它们之间的区别在于备份的范围和备份集的方式。 积累增量备份:在进行积累增量备份时,RMAN 会备份自最后一次完全备份或增量备…...
利用C++nlohmann库解析json文件
json文件示例: 代码运行环境VS2019 一、git下载nlohmann库文件源代码 源代码文件目录 二、利用VS2019新建工程,并配置项目属性 配置VC目录---包含目录 三、项目源代码 #include <iostream> #include <fstream> #include <nlohmann/jso…...

OpenCV 中的光流 (C++/Python)
什么是光流? 光流是一项视频中两个连续帧之间每像素运动估计的任务。基本上,光流任务意味着计算像素的位移矢量作为两个相邻图像之间的对象位移差。光流的主要思想是估计物体由其运动或相机运动引起的位移矢量。 理论基础 假设我们有一个灰度图像——具有像素强度的矩阵。我…...
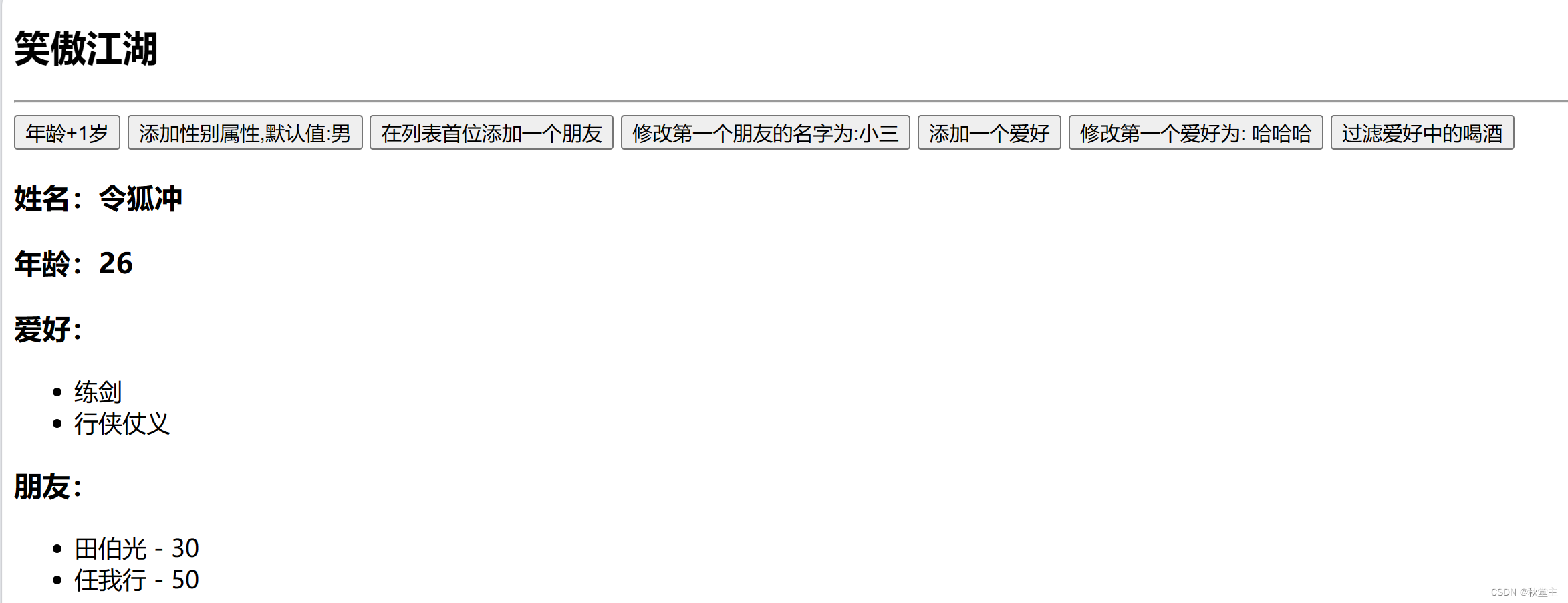
第9集丨Vue 江湖 —— 监测数据原理
目录 一、修改数据时的一个问题1.1 现象一1.2 现象二 二、Vue监测数据原理2.1 模拟一个数据监测2.2 数据劫持2.3 Vue.set()/vm.$set()2.4 基本原理2.4.1 如何监测对象中的数据?2.4.2 如何监测数组中的数据?2.4.3 修改数组中的某个元素 2.5 案例2.5.1 需求功能2.5.2 实现 一、…...

【YOLO】替换骨干网络为轻量级网络MobileNet3
替换骨干网络为轻量级网络MobileNet_v3 上一章 模型网络结构解析&增加小目标检测 文章目录 替换骨干网络为轻量级网络MobileNet_v3前言一、MobileNetV3介绍二、MobileNetV2&MobileNetV3三、MobileNetV3网络结构1. 结构查看2. 查看每层featuremap大小三、YOLOV5替换骨干…...
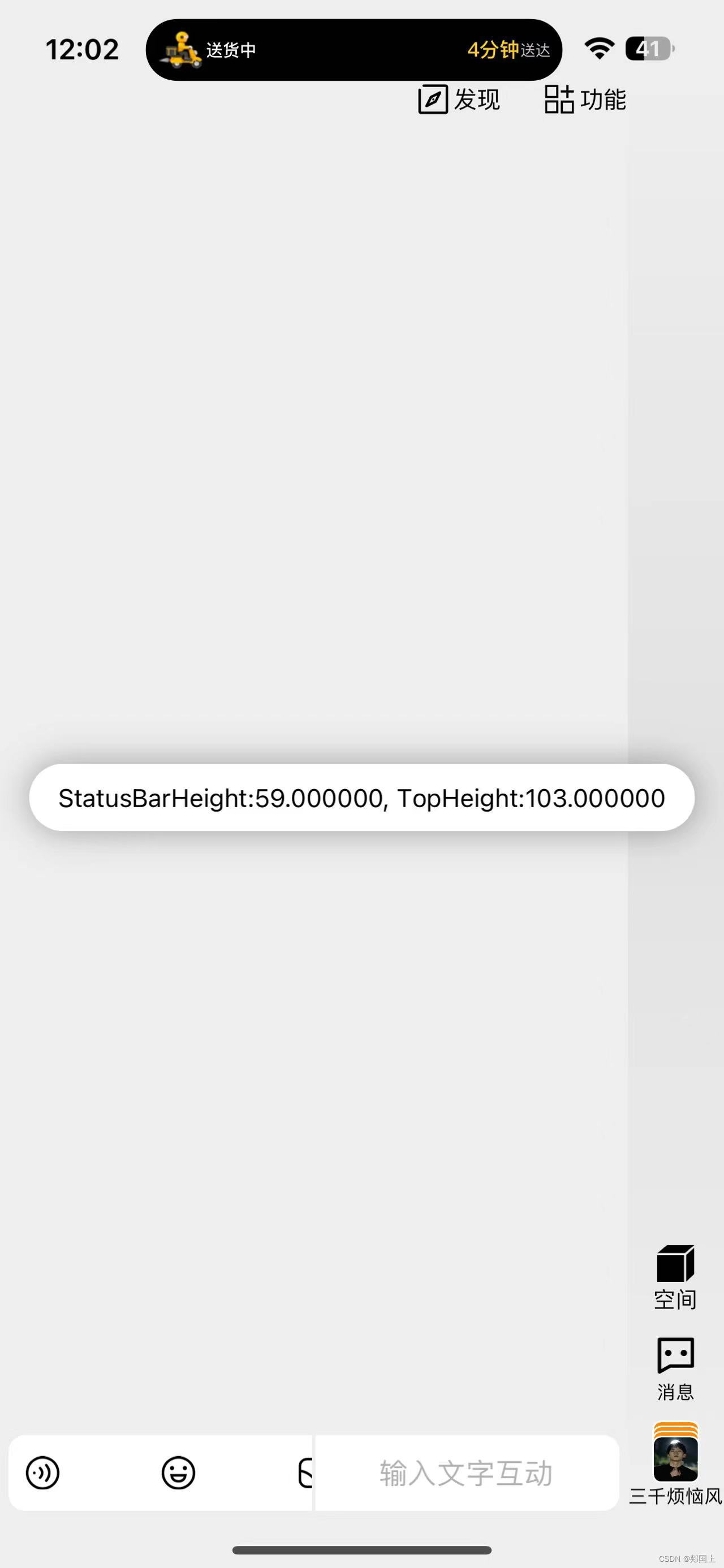
如何识别手机是否有灵动岛(dynamic island)
如何识别手机是否有灵动岛(dynamic island) 灵动岛是苹果2022年9月推出的iPhone 14 Pro、iPhone 14 Pro Max首次出现,操作系统最低是iOS16.0。带灵动岛的手机在竖屏时顶部工具栏大于等于51像素。 #define isHaveDynamicIsland ({ BOOL isH…...

Linux设备树简介
一、起源 减少垃圾代码 减轻驱动开发工作量 驱动代码和设备信息分离 参考Open Fireware设计 用来记录硬件平台中各种硬件设备的属性信息 二、基本组成 两种源文件: xxxxx.dts dts是device tree source的缩写 xxxxx.dtsi dtsi是device tree source include的…...

Ubuntu类IOS主题设置
1.依次执行下面三条命令: sudo apt install gnome-shell-extensions sudo apt install gnome-tweak-tool sudo apt install chrome-gnome-shell2.下载主题,也是命令: git clone <https://github.com/qingchendelaike/GNOME-OSX-II-Theme…...
RabbitMQ学习——发布订阅/fanout模式 topic模式 rabbitmq回调确认 延迟队列(死信)设计
目录 引出点对点(simple)Work queues 一对多发布订阅/fanout模式以登陆验证码为例pom文件导包application.yml文件rabbitmq的配置生产者生成验证码,发送给交换机消费者消费验证码 topic模式配置类增加配置生产者发送信息进行发送控制台查看 rabbitmq回调确认配置类验…...
Leetcode算法递归类—合并两个有序链表
目录 21. 合并两个有序链表 题解: 代码: 将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 示例 1: 输入:l1 [1,2,4], l2 [1,3,4] 输出:[1,1,2,3,4,4]示例 2&a…...
YOLOv5可视化界面
Pyside6可视化界面 安装Pyside6 激活之前的虚拟环境yolov5 在该环境的终端输入以下命令 pip install -i https://pypi.tuna.tsinghua.edu.cn/simple pyside6输入where python找到当前使用的Python的路径 找到该路径下的designer.exe文件(/Lib/site-packages/PySi…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...
