Java课题笔记~ AspectJ 对 AOP 的实现(掌握)
AspectJ 对 AOP 的实现(掌握)
对于 AOP 这种编程思想,很多框架都进行了实现。Spring 就是其中之一,可以完成面向切面编程。然而,AspectJ 也实现了 AOP 的功能,且其实现方式更为简捷,使用更为方便,而且还支持注解式开发。所以,Spring 又将 AspectJ 的对于 AOP 的实现也引入到了自己的框架中。
在 Spring 中使用 AOP 开发时,一般使用 AspectJ 的实现方式。
AspectJ 简介
AspectJ 是一个优秀面向切面的框架,它扩展了 Java 语言,提供了强大的切面实现。
官网地址:The AspectJ Project | The Eclipse FoundationThe Eclipse Foundation - home to a global community, the Eclipse IDE, Jakarta EE and over 415 open source projects, including runtimes, tools and frameworks.http://www.eclipse.org/aspectj/
AspetJ 是 Eclipse 的开源项目,官网介绍如下:

a seamless aspect-oriented extension to the Javatm programming language
(一种基于 Java 平台的面向切面编程的语言)
Java platform compatible(兼容 Java 平台,可以无缝扩展)
easy to learn and use(易学易用)
AspectJ 的通知类型(理解)
AspectJ 中常用的通知有五种类型:
(1)前置通知
(2)后置通知
(3)环绕通知
(4)异常通知
(5)最终通知
AspectJ 的切入点表达式(掌握)
AspectJ 定义了专门的表达式用于指定切入点。表达式的原型是:
execution(modifiers-pattern? ret-type-pattern declaring-type-pattern?namepattern(param-pattern) throws-pattern?) 解释:
modifiers-pattern] 访问权限类型
ret-type-pattern 返回值类型
declaring-type-pattern 包名类名
name-pattern(param-pattern) 方法名(参数类型和参数个数)
throws-pattern 抛出异常类型
?表示可选的部分
以上表达式共 4 个部分。
execution(访问权限 方法返回值 方法声明(参数) 异常类型)
切入点表达式要匹配的对象就是目标方法的方法名。
execution 表达式中明显就是方法的签名。注意:表达式中黑色文字表示可省略部分,各部分间用空格分开。在其中可以使用以下符号:

举例:
- execution(public * *(..)) 指定切入点为:任意公共方法。
- execution(* set*(..)) 指定切入点为:任何一个以“set”开始的方法。
- execution(* com.xyz.service..(..)) 指定切入点为:定义在 service 包里的任意类的任意方法。
- execution(* com.xyz.service...(..)) 指定切入点为:定义在 service 包或者子包里的任意类的任意方法。“..”出现 在类名中时,后面必须跟“*”,表示包、子包下的所有类。
- execution(* ..service..*(..)) 指定所有包下的 serivce 子包下所有类(接口)中所有方法为切入点
- execution(* .service..*(..)) 指定只有一级包下的 serivce 子包下所有类(接口)中所有方法为切入点
- execution(* .ISomeService.(..)) 指定只有一级包下的 ISomeSerivce 接口中所有方法为切入点
- execution(* ..ISomeService.(..)) 指定所有包下的 ISomeSerivce 接口中所有方法为切入点
- execution(* com.xyz.service.IAccountService.*(..)) 指定切入点为:IAccountService 接口中的任意方法。
- execution(* com.xyz.service.IAccountService+.*(..)) 指定切入点为:IAccountService 若为接口,则为接口中的任意方法及其所有 实现类中的任意方法;若为类,则为该类及其子类中的任意方法。
- execution(* joke(String,int))) 指定切入点为:所有的 joke(String,int)方法,且 joke()方法的第一个参数是 String,第二个参数是 int。如果方法中的参数类型是 java.lang 包下的类,可 以直接使用类名,否则必须使用全限定类名,如 joke( java.util.List, int)。
- execution(* joke(String,*))) 指定切入点为:所有的 joke()方法,该方法第一个参数为 String,第二个参数 可以是任意类型,如 joke(String s1,String s2)和 joke(String s1,double d2) 都是,但 joke(String s1,double d2,String s3)不是。
- execution(* joke(String,..))) 指定切入点为:所有的 joke()方法,该方法第一个参数为 String,后面可以有 任意个参数且参数类型不限,如 joke(String s1)、joke(String s1,String s2)和 joke(String s1,double d2,String s3)都是。
- execution(* joke(Object)) 指定切入点为:所有的 joke()方法,方法拥有一个参数,且参数是 Object 类 型。joke(Object ob)是,但,joke(String s)与 joke(User u)均不是。
- execution(* joke(Object+))) 指定切入点为:所有的 joke()方法,方法拥有一个参数,且参数是 Object 类型 或该类的子类。不仅 joke(Object ob)是,joke(String s)和 joke(User u)也 是。
相关文章:

Java课题笔记~ AspectJ 对 AOP 的实现(掌握)
AspectJ 对 AOP 的实现(掌握) 对于 AOP 这种编程思想,很多框架都进行了实现。Spring 就是其中之一,可以完成面向切面编程。然而,AspectJ 也实现了 AOP 的功能,且其实现方式更为简捷,使用更为方便,而且还支…...
npm 报错 cb() never called!
不知道有没有跟我一样的情况,在使用npm i的时候一直报错:cb() never called! 换了很多个node版本,还是不行,无法解决这个问题 百度也只是让降低node版本请缓存,gpt给出的解决方案也是同样的 但是缓存清过很多次了&a…...

finally有什么作用以及常用场景
在Java中,finally是一个关键字,用于定义一个代码块,该代码块中的代码无论是否发生异常都会被执行。finally块通常用于确保在程序执行过程中资源的释放和清理。 使用场景: 1. 资源释放:finally块经常用于释放打开的资…...

Python web实战之Django URL路由详解
概要 技术栈:Python、Django、Web开发、URL路由 Django是一种流行的Web应用程序框架,它采用了与其他主流框架类似的URL路由机制。URL路由是指将传入的URL请求映射到相应的视图函数或处理程序的过程。 什么是URL路由? URL路由是Web开发中非常…...
10-数据结构-队列(C语言)
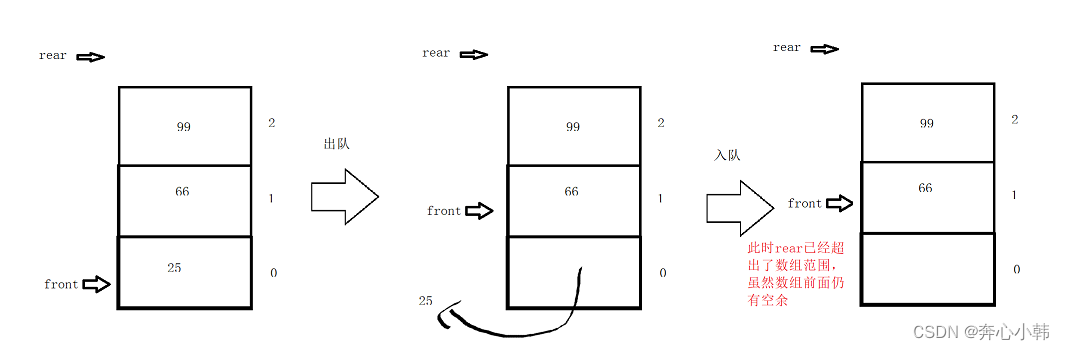
队列 目录 目录 队列 一、队列基础知识 二、队列的基本操作 1.顺序存储 编辑 (1)顺序存储 (2)初始化及队空队满 (3)入队 (4)出队 (5)打印队列 &…...

面试之快速学习C++11 - 右值 移动构造 std::move
C11右值引用 字面意思,以引用传递的方式使用c右值左值和右值,左值是lvalue loactor value 存储在内存中,有明确存储地址的数据, 右值rvalue read value , 指的是那些可以提供数据值的数据(不一定可以寻址,…...
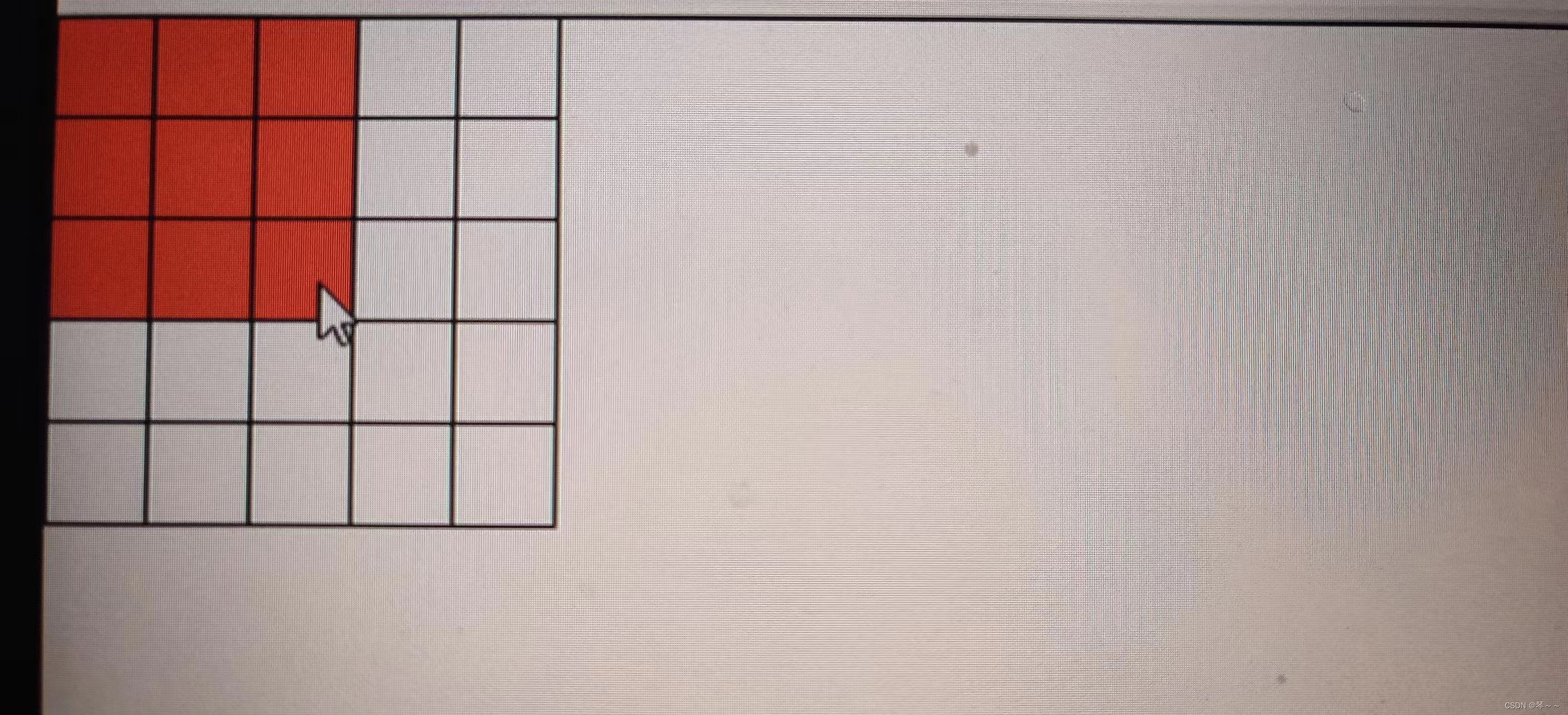
vue实现5*5宫格当鼠标滑过选中的正方形背景颜色统一变色
vue实现5*5宫格当鼠标滑过选中的正方形背景颜色统一变色 1、实现的效果 2、完整代码展示 <template><div id"app" mouseleave"handleMouseLeave({row: 0, col: 0 })"><div v-for"rowItem in squareNumber" :key"rowItem…...

2023-08-09 LeetCode每日一题(整数的各位积和之差)
2023-08-09每日一题 一、题目编号 1281. 整数的各位积和之差二、题目链接 点击跳转到题目位置 三、题目描述 给你一个整数 n,请你帮忙计算并返回该整数「各位数字之积」与「各位数字之和」的差。 示例1: 示例2: 提示: 1 …...
EditPlus连接Linux系统远程操作文件
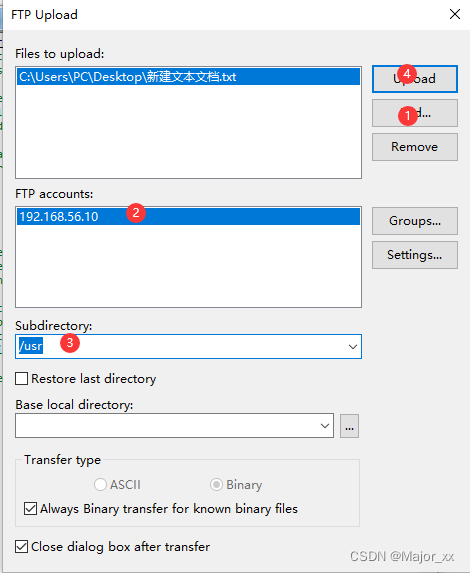
EditPlus是一套功能强大的文本编辑器! 1.File ->FTP->FTP Settings; 2.Add->Description->FTP server->Username->Password->Subdirectory->Advanced Options 注意:这里的Subdirectory设置的是以后上传文件的默认…...

JVM 垃圾回收
垃圾回收算法 标记-清除算法(Mark and Sweep) 标记-清除算法分为两个阶段。在标记阶段,垃圾收集器会标记所有活动对象;在清除阶段,垃圾收集器会清除所有未标记的对象。标记-清除算法存在的问题是会产生内存碎片&#…...
编程中的宝藏:二分查找
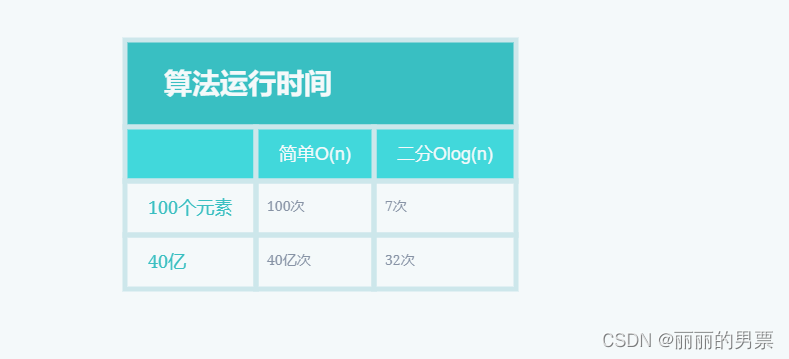
二分查找 假设你需要在电话簿中找到一个以字母 “K” 开头的名字(虽然现在谁还在用电话簿呢!)。你可以从头开始翻页,直到进入以 “K” 打头的部分。然而,更明智的方法是从中间开始,因为你知道以 “K” 打头…...
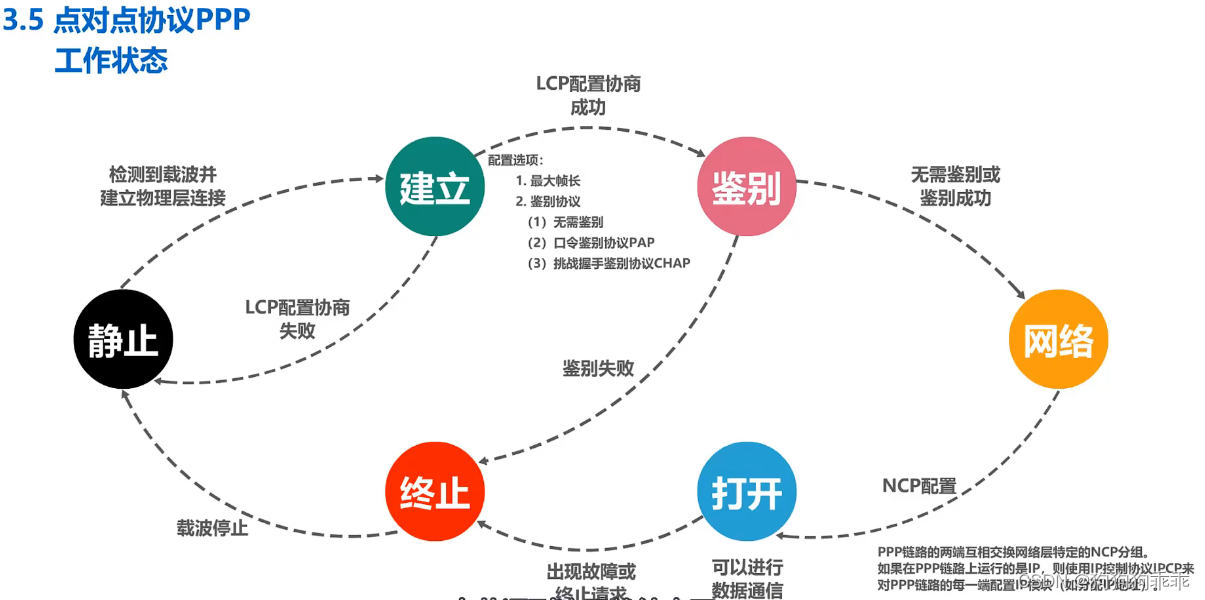
计算机网络 数据链路层
...

如何维护自己的电脑
目录 1、关于电脑选择的建议 1.1、价格预算 1.2、明确需求 1.3、电脑配置 1.4、分辨率 1.5、续航能力 1.6、品牌选择 1.7、用户评测 1.8、各个电商平台对比 1.9、最后决策 2、我的选择 3、电脑保养 3.1 外部清洁 3.2 安装软件 3.3 优化操作系统 3.4 维护硬件设…...

智能优化算法——哈里鹰算法(Matlab实现)
目录 1 算法简介 2 算法数学模型 2.1.全局探索阶段 2.2 过渡阶段 2.3.局部开采阶段 3 求解步骤与程序框图 3.1 步骤 3.2 程序框图 4 matlab代码及结果 4.1 代码 4.2 结果 1 算法简介 哈里斯鹰算法(Harris Hawks Optimization,HHO),是由Ali As…...
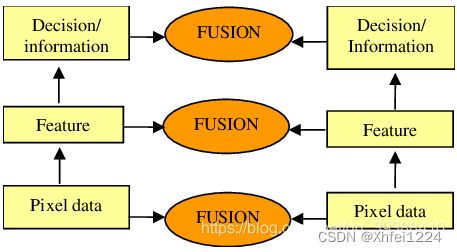
【深度学习】多粒度、多尺度、多源融合和多模态融合的区别
多粒度(multiresolution)和多尺度(multiscale) 多粒度(multiresolution)和多尺度(multiscale)都是指在不同的空间或时间尺度上对数据或信号进行分析和处理。其中 多尺度࿱…...

利用SCCM进行横向移动
01SCCM介绍 SCCM全名为System Center Configuration Manager,从版本1910开始,微软官方将其从Microsoft System Center产品移除,重新命名为Microsoft Endpoint Configuration Manager(ConfigMgr),其可帮助 …...
Nginx 负载均衡
Nginx 负载均衡 负载均衡由反向代理来实现的 其中反向代理分为七层代理和四层代理,一般常用的是七层代理,接下来分别介绍一些 NGINX 七层代理 七层是最常用的反向代理方式,只能配置在Nginx配置文件的http模块。 配置方法名称:…...
Java课题笔记~ ServletConfig
概念:代表整个web应用,可以和程序的容器(服务器)来通信 <?xml version"1.0" encoding"UTF-8"?> <web-app xmlns"http://java.sun.com/xml/ns/javaee"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instan…...

oracle的异常处理
oracle提供了预定义例外、非预定义例外和自定义例外三种类型。其中: l预定义例外用于处理常见的oracle错误; l非预定义例外用于处理预定义所不能处理的oracle错误; l自定义例外处理与oracle错误无关的其他情况。 Oracle代码编写过程中&am…...
【MySQL】MySQL数据类型
文章目录 一、数据类型的分类二、tinyint类型2.1 创建有符号数值2.2 创建无符号数值 三、bit类型三、浮点类型3.1 float3.2 decimal类型 四、字符串类型4.1 char类型4.2 varchar类型 五、日期和时间类型六、枚举和集合类型6.1 enum的枚举值和set的位图结构6.2 查询集合find_in_…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...
