智能优化算法——哈里鹰算法(Matlab实现)
目录
1 算法简介
2 算法数学模型
2.1.全局探索阶段
2.2 过渡阶段
2.3.局部开采阶段
3 求解步骤与程序框图
3.1 步骤
3.2 程序框图
4 matlab代码及结果
4.1 代码
4.2 结果
1 算法简介
哈里斯鹰算法(Harris Hawks Optimization,HHO),是由Ali Asghar Heidari和Seyedali Mrjaili于2019年提出的一种新型仿生智能优化算法。该算法模仿哈里斯鹰捕食特点,结合Levy飞行(Levy Flights)实现对复杂多维问题求解。研究表明该新型算法具有良好的性能。在HHO中,哈里斯鹰是候选解,猎物随迭代逼近最优解.HHO算法包括两个阶段:全局探索阶段、局部开采阶段.
2 算法数学模型
2.1.全局探索阶段
在这一阶段中,哈里斯鹰处于等待状态。仔细检查和监控搜索空间[b , ub]以发现猎物。根据两种策略在随机的地方寻找猎物,迭代时以概率q进行位置更新。数学表达式如下:
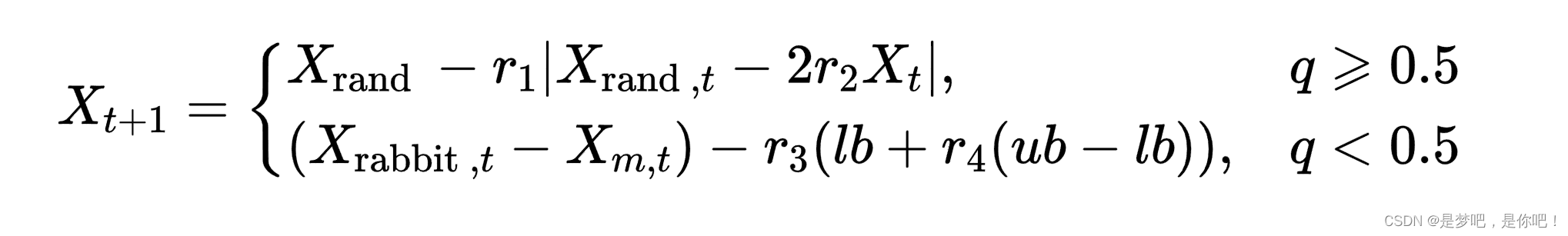
式中,
和
编辑分别为哈里斯鹰第t+1次和第t次迭代时的位置,Xrabbit,t表示猎物第t次迭代时的位置,q和r1,r2,r3,r4是区间(0,1)内的随机数字,lb是搜索空间的下界,ub是搜索空间的上界,Xrand,t表示第t次迭代时哈里斯鹰的随机位置,Xm,t表示第t次迭代时哈里斯鹰的平均位置,公式如下:
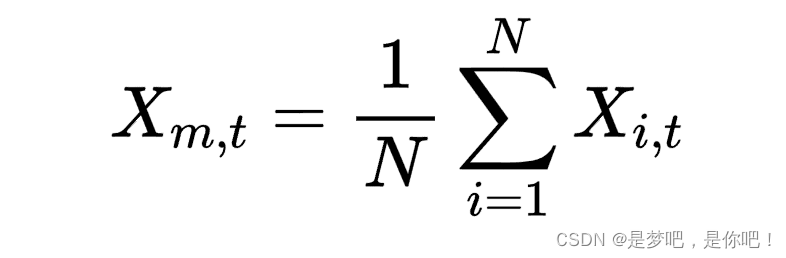
2.2 过渡阶段
该阶段用于保持探索和开采之间适当的平衡。HHO通过猎物的能量方程实现从探索到开采的过渡。
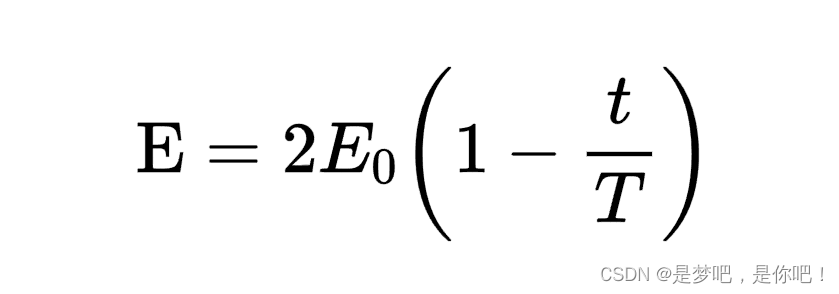
式中,E表示猎物逃跑的能量,
是猎物能量的初始状态,公式为E0= 2*rand - 1,rand是(0,1)之间的随机数字,T为最大迭代次数,t为当前迭代次数.当E≥1时,哈里斯鹰算法将执行全局探索;否则,HHO算法进入局部开采。
2.3.局部开采阶段
根据猎物的逃跑行为和哈里斯鹰的追逐策略,HHO算法提出了四种可能的策略来模拟攻击行为.用N表示猎物成功逃脱的概率。
(1)软围攻.当E≥0.5,A≥0.5时,猎物有足够的能量且以跳跃的方式逃脱围捕,而哈里斯鹰会逐渐消耗猎物的能量,然后选择最佳的位置突袭俯冲逮捕猎物.更新位置的方程如下:
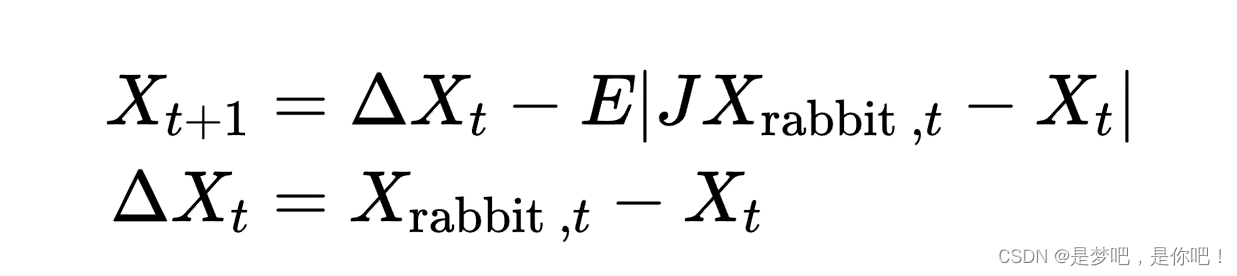
式中,Xt是迭代时猎物与哈里斯鹰的位置之差,J=2(1-r5)表示猎物逃跑过程中的随机跳跃,r5是介于0到1之间的随机数字.
(2)硬围攻.当E<0.5,入≥0.5时,猎物筋疲力尽,哈里斯鹰选择迅速突袭.位置更新如下:
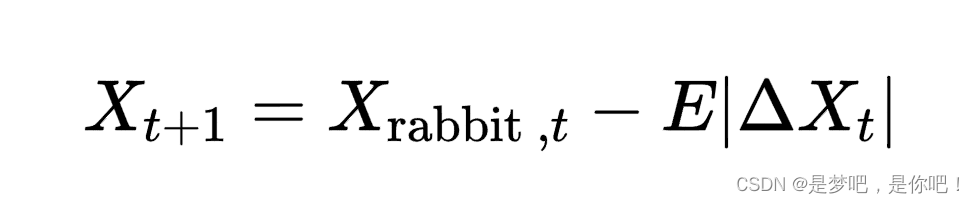
(3)累速俯冲式软围攻.当E>0.5,入<0.5时,猎物有足够的能量E逃跑,哈里斯鹰在突袭之前会建立一个软围攻.为了模拟猎物的逃跑模式和跳跃动作,将levy函数LF集成在HHO算法中.更新位置的策略为:

式中,D为问题维度,S为D维随机行向量.
(4)累速俯冲式硬围攻.当E<0.5,入<0.5时,猎物能量E低,哈里斯鹰在突袭前构建硬围攻捕捉猎物,位置更新如:
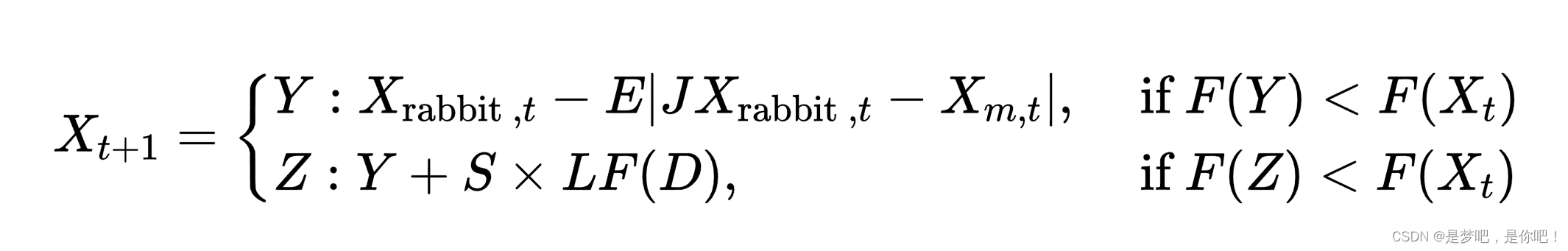
Levy飞行函数公式如下:

式中,u、v是(0,1)之间的随机数,β取常值1.5。
HHO算法用猎物能量E和因子入调节哈里斯鹰和猎物(兔子)之间的四种围捕机制,来实现优化求解问题.
3 求解步骤与程序框图
3.1 步骤
HHO算法的规则描述如下:
1)每次迭代前,判断是否越界并调整,更新猎物位置与适应度值;
2)在搜索阶段,哈里斯鹰拥有两种不同搜索方式,分别针对发现和未发现猎物;
3)野兔的逃逸能量会随着迭代次数增加而自适应减小;
4)当野兔能量降低到某一阈值,将被哈里斯鹰群发现,狩猎从搜索阶段转为围捕突袭阶段;
5)每一次突袭前,兔子都有一定的概率从包围中逃脱;
6)针对兔子的体力,以及是否逃脱包围圈,哈里斯鹰有四种不同的围捕策略;
7)每次围捕最终兔子将会捕获,每次迭代会产生一个新的猎物,该位置将由新一代种群中适应度值最优者占据。
实现步骤
Step1:初始化种群:包括搜索空间的上限和下限,算法的最大迭代次数T。随机初始化种群位置.
Step2:根据适应度函数计算每个个体的适应度值,保存种群最优个体.
Step3:更新猎物逃逸能量E.
Step4:比较E的大小,按位置更新公式或四种策略追捕猎物,更新位置.Step5:对每个个体,计算适应度,更新种群最优的适应度值.
Step6:判断搜索到的结果是否满足停止条件(达到最大迭代次数或满足精度要求),若满足停止条件则输出最优值,否则转到Step3继续运行直到满足条件为止.
3.2 程序框图
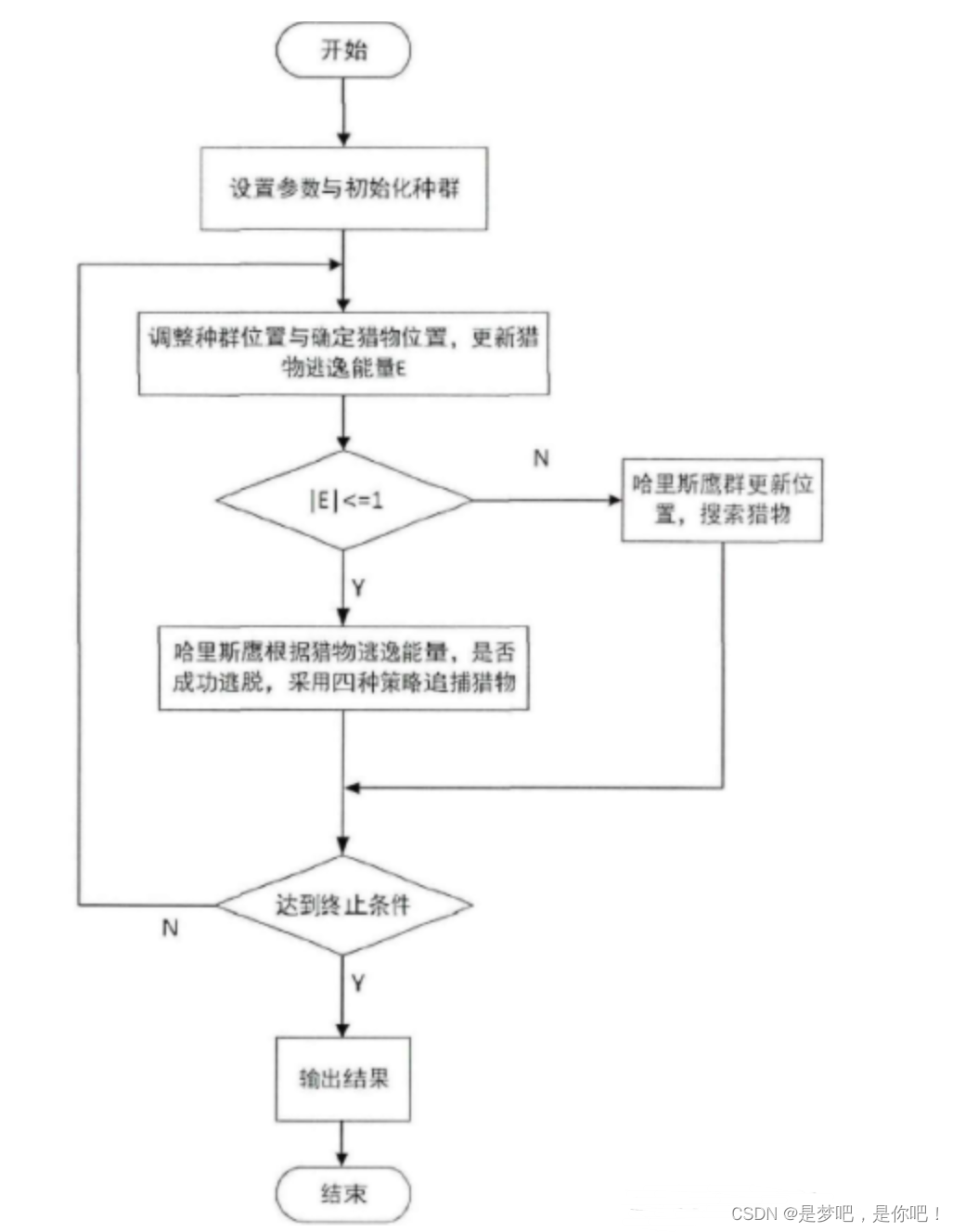
4 matlab代码及结果
4.1 代码
%% 智能优化算法——哈里鹰算法(Matlab实现)
clear
close all
clcSearchAgents_no = 30 ; % 种群规模
dim = 10 ; % 粒子维度
Max_iter = 1000 ; % 迭代次数
ub = 5 ;
lb = -5 ;
%% 初始化猎物位置和逃逸能量
Rabbit_Location=zeros(1,dim);
Rabbit_Energy=inf;%% 初始化种群的位置
Positions= lb + rand(SearchAgents_no,dim).*(ub-lb) ;Convergence_curve = zeros(Max_iter,1);%% 开始循环
for t=1:Max_iterfor i=1:size(Positions,1)% Check boundriesFU=Positions(i,:)>ub;FL=Positions(i,:)<lb;Positions(i,:)=(Positions(i,:).*(~(FU+FL)))+ub.*FU+lb.*FL;% fitness of locationsfitness=sum(Positions(i,:).^2);% Update the location of Rabbitif fitness<Rabbit_EnergyRabbit_Energy=fitness;Rabbit_Location=Positions(i,:);endendE1=2*(1-(t/Max_iter)); % factor to show the decreaing energy of rabbit%% Update the location of Harris' hawksfor i=1:size(Positions,1)E0=2*rand()-1; %-1<E0<1Escaping_Energy=E1*(E0); % escaping energy of rabbitif abs(Escaping_Energy)>=1%% Exploration:% Harris' hawks perch randomly based on 2 strategy:q=rand();rand_Hawk_index = floor(SearchAgents_no*rand()+1);X_rand = Positions(rand_Hawk_index, :);if q<0.5% perch based on other family membersPositions(i,:)=X_rand-rand()*abs(X_rand-2*rand()*Positions(i,:));elseif q>=0.5% perch on a random tall tree (random site inside group's home range)Positions(i,:)=(Rabbit_Location(1,:)-mean(Positions))-rand()*((ub-lb)*rand+lb);endelseif abs(Escaping_Energy)<1%% Exploitation:% Attacking the rabbit using 4 strategies regarding the behavior of the rabbit%% phase 1: surprise pounce (seven kills)% surprise pounce (seven kills): multiple, short rapid dives by different hawksr=rand(); % probablity of each eventif r>=0.5 && abs(Escaping_Energy)<0.5 % Hard besiegePositions(i,:)=(Rabbit_Location)-Escaping_Energy*abs(Rabbit_Location-Positions(i,:));endif r>=0.5 && abs(Escaping_Energy)>=0.5 % Soft besiegeJump_strength=2*(1-rand()); % random jump strength of the rabbitPositions(i,:)=(Rabbit_Location-Positions(i,:))-Escaping_Energy*abs(Jump_strength*Rabbit_Location-Positions(i,:));end%% phase 2: performing team rapid dives (leapfrog movements)if r<0.5 && abs(Escaping_Energy)>=0.5% Soft besiege % rabbit try to escape by many zigzag deceptive motionsJump_strength=2*(1-rand());X1=Rabbit_Location-Escaping_Energy*abs(Jump_strength*Rabbit_Location-Positions(i,:));if sum(X1.^2)<sum(Positions(i,:).^2) % improved movePositions(i,:)=X1;else % hawks perform levy-based short rapid dives around the rabbit%Levy flightbeta=1.5;sigma=(gamma(1+beta)*sin(pi*beta/2)/(gamma((1+beta)/2)*beta*2^((beta-1)/2)))^(1/beta);u=randn(1,dim)*sigma;v=randn(1,dim);step=u./abs(v).^(1/beta);o1=0.01*step;X2=Rabbit_Location-Escaping_Energy*abs(Jump_strength*Rabbit_Location-Positions(i,:))+rand(1,dim).*o1;if (sum(X2.^2)<sum(Positions(i,:).^2))% improved movePositions(i,:)=X2;endendendif r<0.5 && abs(Escaping_Energy)<0.5% Hard besiege % rabbit try to escape by many zigzag deceptive motions% hawks try to decrease their average location with the rabbitJump_strength=2*(1-rand());X1=Rabbit_Location-Escaping_Energy*abs(Jump_strength*Rabbit_Location-mean(Positions));if sum(X1.^2)<sum(Positions(i,:).^2) % improved movePositions(i,:)=X1;else % Perform levy-based short rapid dives around the rabbit%Levy flightbeta=1.5;sigma=(gamma(1+beta)*sin(pi*beta/2)/(gamma((1+beta)/2)*beta*2^((beta-1)/2)))^(1/beta);u=randn(1,dim)*sigma;v=randn(1,dim);step=u./abs(v).^(1/beta);o2=0.01*step;X2=Rabbit_Location-Escaping_Energy*abs(Jump_strength*Rabbit_Location-mean(Positions))+rand(1,dim).*o2;if (sum(X2.^2)<sum(Positions(i,:).^2))% improved movePositions(i,:)=X2;endendend%%endendConvergence_curve(t)=Rabbit_Energy;% Print the progress every 100 iterationsif mod(t,50)==0display(['At iteration ', num2str(t), ' the best fitness is ', num2str(Rabbit_Energy)]);end
end
figure('unit','normalize','Position',[0.3,0.35,0.4,0.35],'color',[1 1 1],'toolbar','none')
subplot(1,2,1);
x = -5:0.1:5;y=x;
L=length(x);
f=zeros(L,L);
for i=1:Lfor j=1:Lf(i,j) = x(i)^2+y(j)^2;end
end
surfc(x,y,f,'LineStyle','none');
xlabel('x_1');
ylabel('x_2');
zlabel('F')
title('Objective space')subplot(1,2,2);
semilogy(Convergence_curve,'Color','r','linewidth',1.5)
title('Convergence_curve')
xlabel('Iteration');
ylabel('Best score obtained so far');axis tight
grid on
box on
legend('HHO')
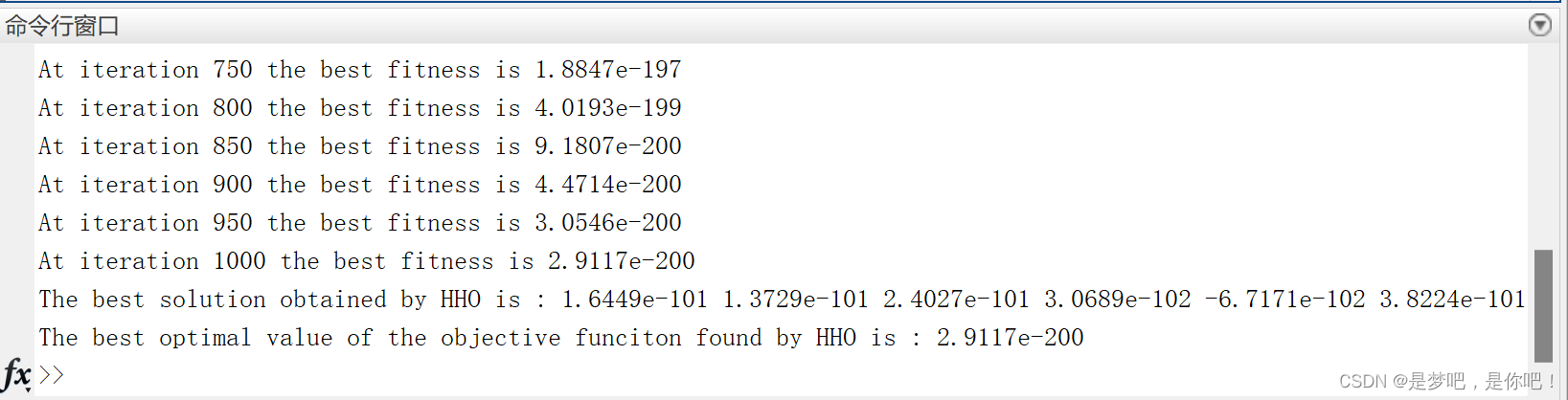
display(['The best solution obtained by HHO is : ', num2str(Rabbit_Location)]);
display(['The best optimal value of the objective funciton found by HHO is : ', num2str(Rabbit_Energy)]);4.2 结果
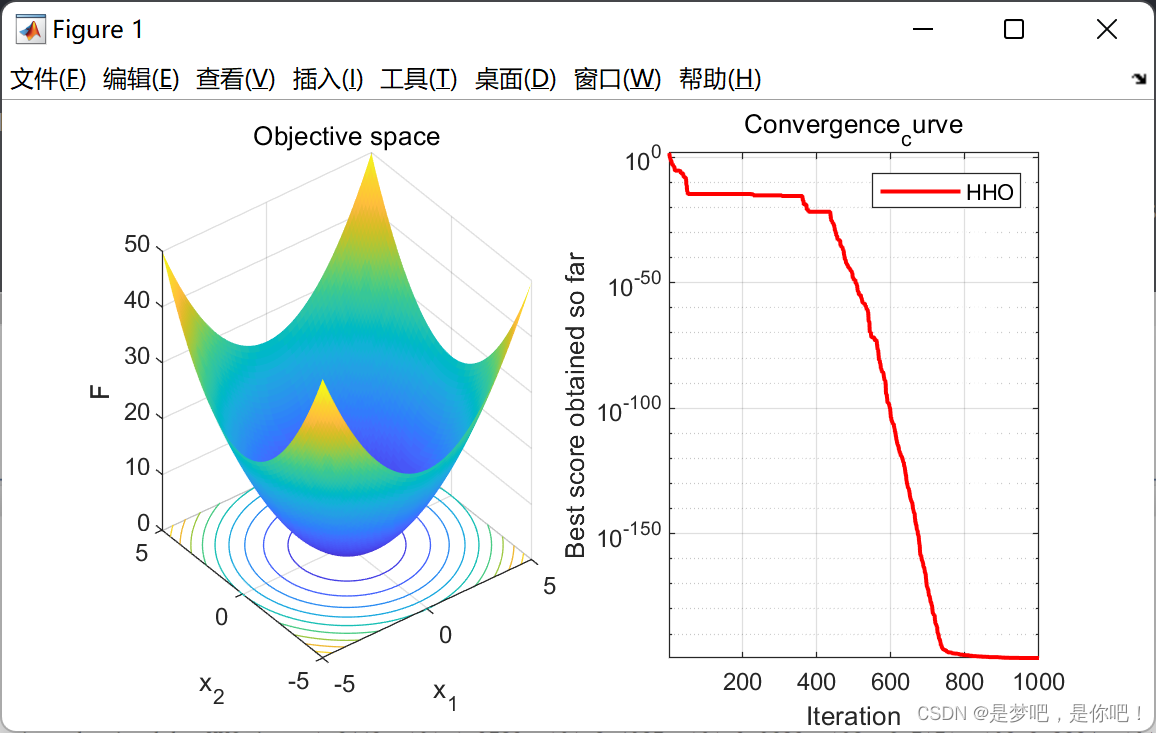
相关文章:

智能优化算法——哈里鹰算法(Matlab实现)
目录 1 算法简介 2 算法数学模型 2.1.全局探索阶段 2.2 过渡阶段 2.3.局部开采阶段 3 求解步骤与程序框图 3.1 步骤 3.2 程序框图 4 matlab代码及结果 4.1 代码 4.2 结果 1 算法简介 哈里斯鹰算法(Harris Hawks Optimization,HHO),是由Ali As…...
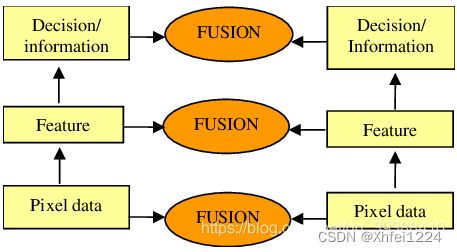
【深度学习】多粒度、多尺度、多源融合和多模态融合的区别
多粒度(multiresolution)和多尺度(multiscale) 多粒度(multiresolution)和多尺度(multiscale)都是指在不同的空间或时间尺度上对数据或信号进行分析和处理。其中 多尺度࿱…...

利用SCCM进行横向移动
01SCCM介绍 SCCM全名为System Center Configuration Manager,从版本1910开始,微软官方将其从Microsoft System Center产品移除,重新命名为Microsoft Endpoint Configuration Manager(ConfigMgr),其可帮助 …...
Nginx 负载均衡
Nginx 负载均衡 负载均衡由反向代理来实现的 其中反向代理分为七层代理和四层代理,一般常用的是七层代理,接下来分别介绍一些 NGINX 七层代理 七层是最常用的反向代理方式,只能配置在Nginx配置文件的http模块。 配置方法名称:…...
Java课题笔记~ ServletConfig
概念:代表整个web应用,可以和程序的容器(服务器)来通信 <?xml version"1.0" encoding"UTF-8"?> <web-app xmlns"http://java.sun.com/xml/ns/javaee"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instan…...

oracle的异常处理
oracle提供了预定义例外、非预定义例外和自定义例外三种类型。其中: l预定义例外用于处理常见的oracle错误; l非预定义例外用于处理预定义所不能处理的oracle错误; l自定义例外处理与oracle错误无关的其他情况。 Oracle代码编写过程中&am…...
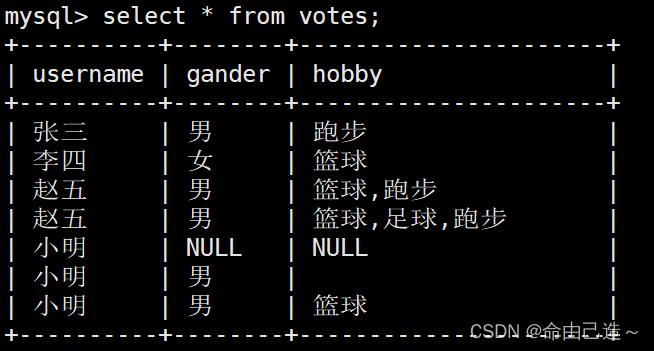
【MySQL】MySQL数据类型
文章目录 一、数据类型的分类二、tinyint类型2.1 创建有符号数值2.2 创建无符号数值 三、bit类型三、浮点类型3.1 float3.2 decimal类型 四、字符串类型4.1 char类型4.2 varchar类型 五、日期和时间类型六、枚举和集合类型6.1 enum的枚举值和set的位图结构6.2 查询集合find_in_…...
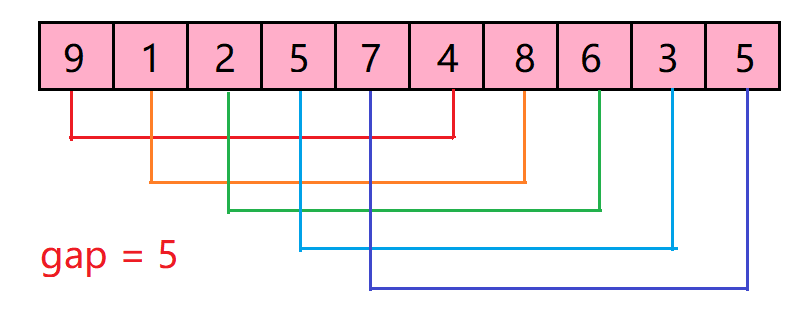
【数据结构与算法】十大经典排序算法-希尔排序
🌟个人博客:www.hellocode.top 🏰Java知识导航:Java-Navigate 🔥CSDN:HelloCode. 🌞知乎:HelloCode 🌴掘金:HelloCode ⚡如有问题,欢迎指正&#…...

docker 常用命令
1. 搜索并下载镜像 docker search bundlefusion # 搜索docker pull jhljx/bundlefusion # 将远程仓库文件下载到本地2. 用镜像创建容器 docker run -it --namebundlefusion colec777/bundlefusion-cu11.4-cudagl:v8 /bin/bash # 创建并运行 exit # 退出终端 sudo docker cont…...
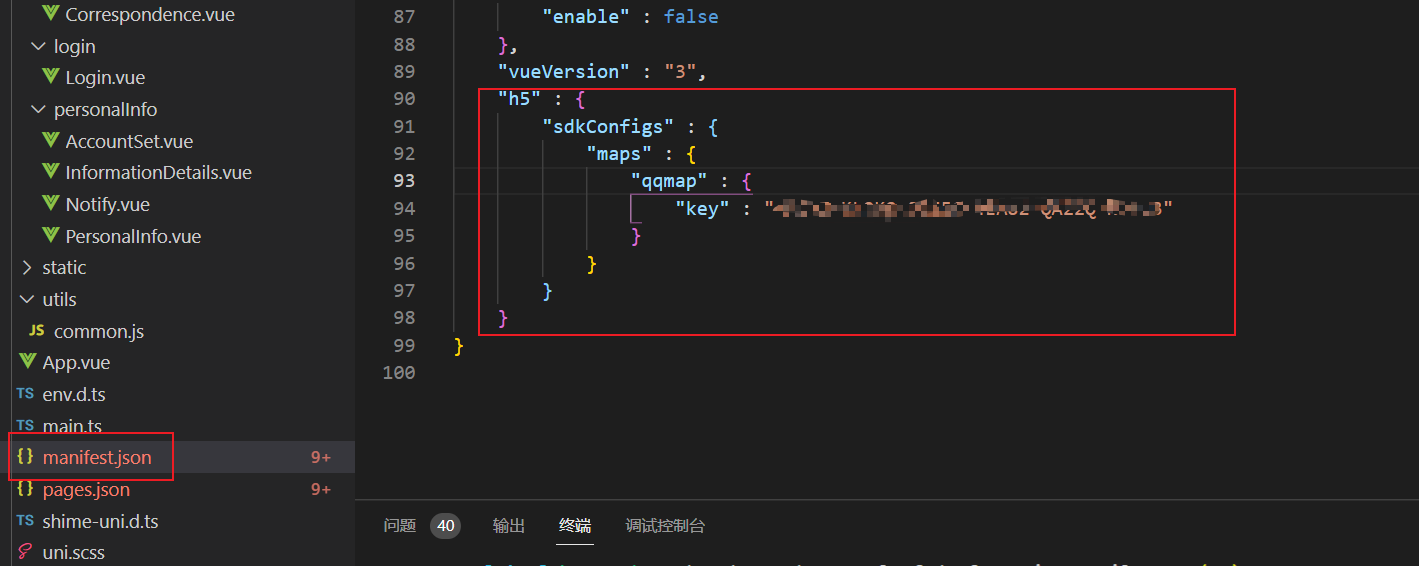
uniapp微信小程序中打开腾讯地图获取用户位置信息
实现的效果 第一步:首先登录微信公众平台 , 需要用到AppID 第二步: 注册登录腾讯位置服务 注册需要手机号和邮箱确认,然后创建应用 创建后点击添加key 添加后会生成key,后面会用到这个key 第三步: 登录微信公众平台&a…...
嵌入式领域:人才供需失衡,发展潜力巨大
嵌入式技术正快速发展,ARM处理器、嵌入式操作系统、LINUX等技术助力嵌入式领域崛起。然而,行业新颖且门槛高,缺乏专业指导。因此,嵌入式人才稀缺,身价水涨船高。 未来几年,嵌入式系统将在信息化、智能化、…...

python 书籍
python高手进阶之路 10册 QQ:417398600...

Debian纯净系统安装php常用扩展和程序
适用于 php-fpm debian容器 mysql扩展 docker-php-ext-install pdo_mysql docker-php-ext-install mysqliredis扩展 pecl install redis docker-php-ext-enable redis# pecl无法装就: docker-php-source extract # 创建并初始化 /usr/src/php目录(扩展…...
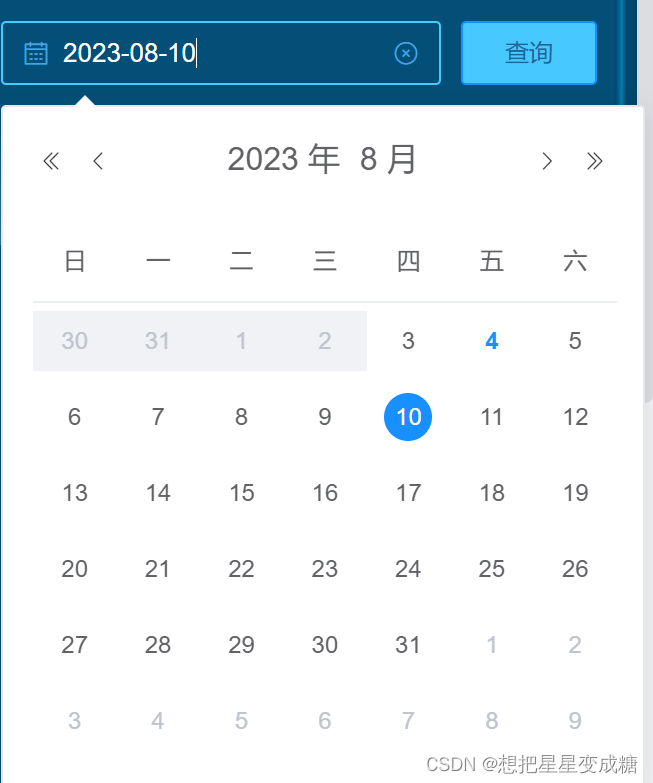
vue+element中如何设置单个el-date-picker开始时间和结束时间关联
功能:选了开始时间,则结束时间只能选择开始时间之后的;选了结束时间,则开始时间只能选择结束时间之前的 重点是picker-options属性 图示: 代码展示: // body 内部<el-form-item><el-date-pickerv-model&qu…...

二次封装ajax和axios
ajax app.config.globalProperties.$http function(url, method, data, async, fun) {$.ajax({url: baseUrl url, //请求地址type: method, //请求方式dataType: json, //数据类型contentType: "application/json",xhrFields: { //跨域设置withCredentials: t…...
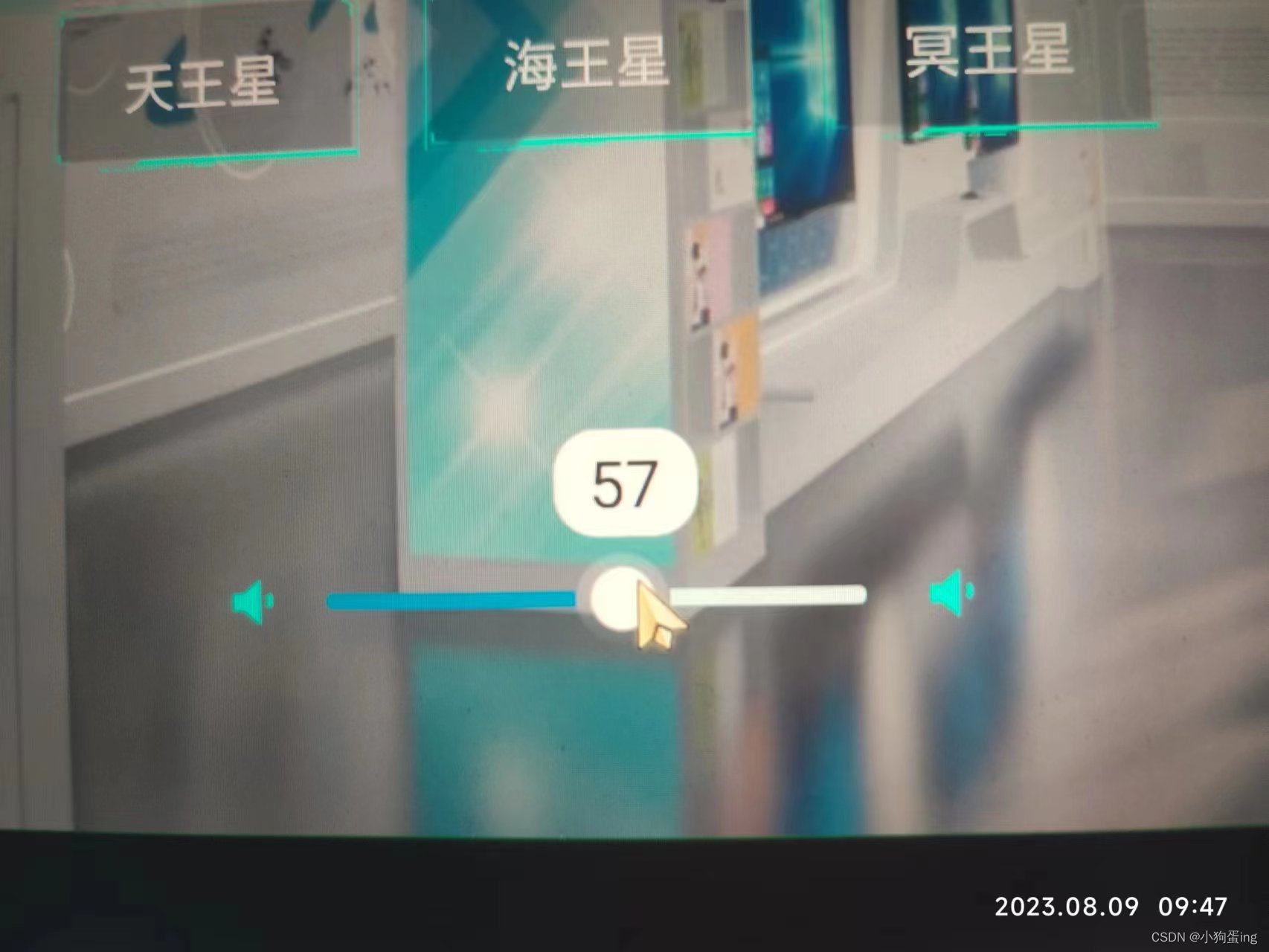
Android进阶之SeekBar动态显示进度
SeekBar 在开发中并不陌生,默认的SeekBar是不显示进度的,当然用吐司或者文案在旁边实时显示也是可以的,那能不能移动的时候才显示,默认不显示呢,当然网上花哨的三方工具类太多了,但是我只是单纯的想在SeekBar的基础上去添加一个可以跟随移动显示的气泡而…...

企业计算机服务器中了locked勒索病毒怎么办,如何预防勒索病毒攻击
计算机服务器是企业的关键信息基础设备,随着计算机技术的不断发展,企业的计算机服务器也成为了众多勒索者的攻击目标,勒索病毒成为当下计算机服务器的主要攻击目标。近期,我们收到很多企业的求助,企业的服务器被locked…...
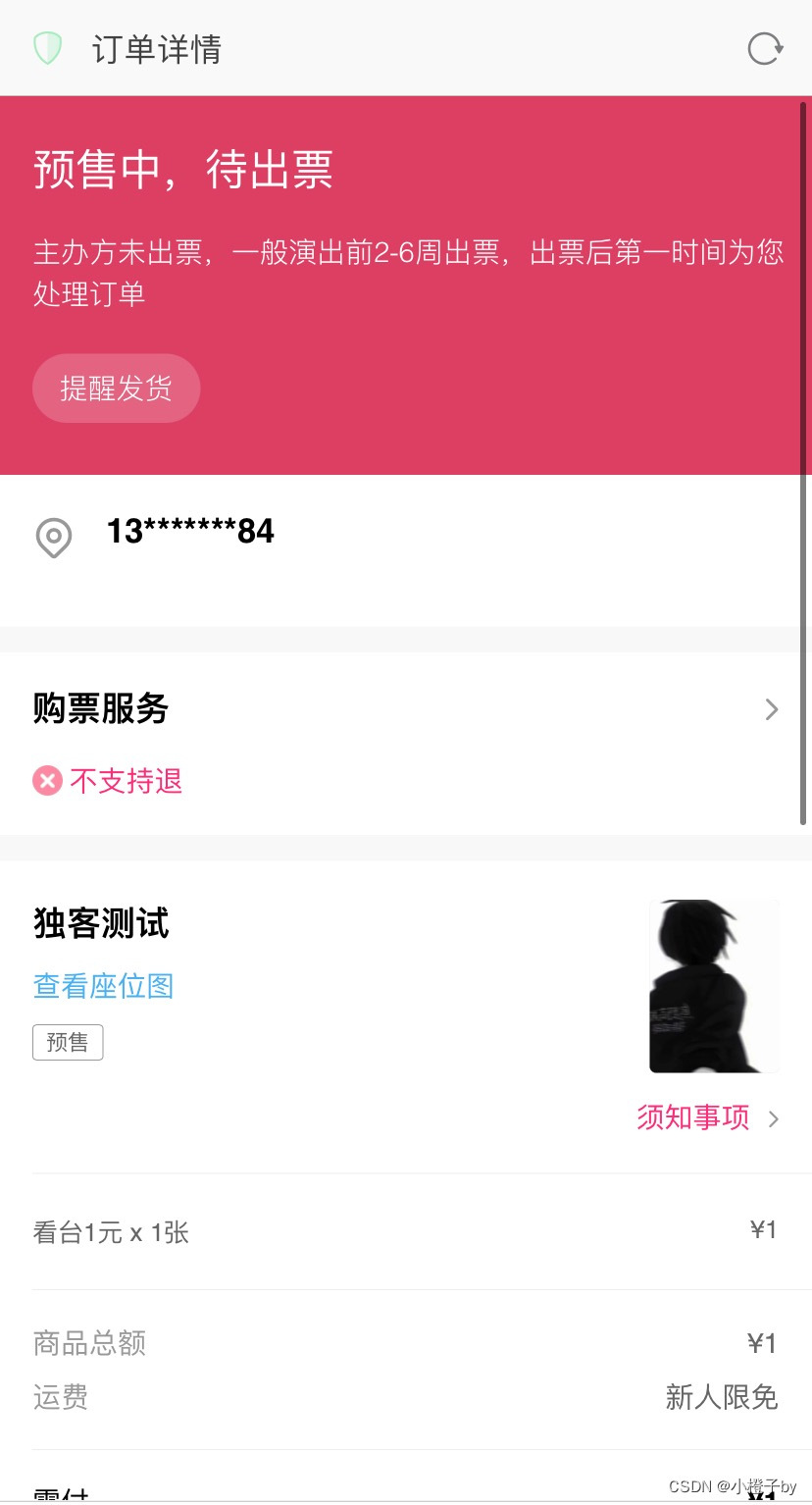
大麦订单截图 一键生成订单截图
新版付款图样式展示 这个样式图就是在大麦刚付款完的一个订单截图,它的状态是等待卖家发货 下滑下载源码 下载源码:https://pan.baidu.com/s/16lN3gvRIZm7pqhvVMYYecQ?pwd6zw3...
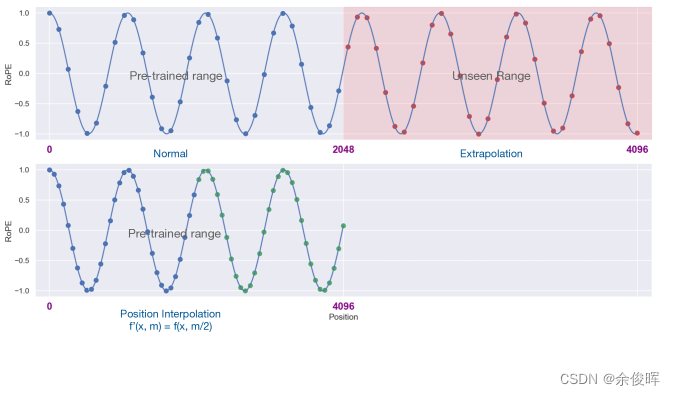
LLaMA长度外推高性价比trick:线性插值法及相关改进源码阅读及相关记录
前言 最近,开源了可商用的llama2,支持长度相比llama1的1024,拓展到了4096长度,然而,相比GPT-4、Claude-2等支持的长度,llama的长度外推显得尤为重要,本文记录了三种网络开源的RoPE改进方式及相…...

中国信息安全测评中心CISP家族认证一览
随着国家对网络安全的重视,中国信息安全测评中心根据国家政策、未来趋势、重点内容陆续增添了很多CISP细分认证。 今日份详细介绍,部分CISP及其子品牌相关认证内容,一定要收藏哟! 校园版CISP NISP国家信息安全水平考试ÿ…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...
