【数据结构与算法】十大经典排序算法-希尔排序
🌟个人博客:www.hellocode.top
🏰Java知识导航:Java-Navigate
🔥CSDN:HelloCode.
🌞知乎:HelloCode
🌴掘金:HelloCode
⚡如有问题,欢迎指正,一起学习~~
希尔排序是一种插入排序的改进版本,旨在解决插入排序在处理大规模数据时的效率问题。通过将数组分为多个子序列并对这些子序列进行局部排序,希尔排序逐步将元素“分组”并逐渐接近它们的最终排序位置。这种逐步的排序方式可以有效减少逆序对的数量,从而加快整体排序过程。
基本思想
这里使用五分钟学算法大佬的动图,很清晰
- 希尔排序将数组分成若干个子序列,每个子序列包含间隔为 h 的元素,称为 h-子序列。
- 对每个 h-子序列应用插入排序,以实现局部排序。
- 不断缩小 h 的值,重复步骤 2,直到 h 为 1。此时,整个序列基本有序,只需对相邻元素进行插入排序即可。
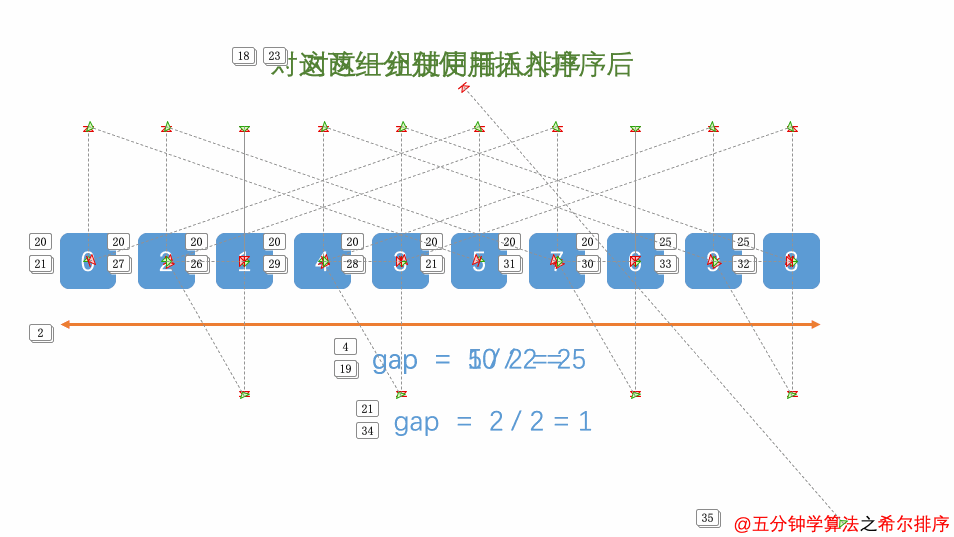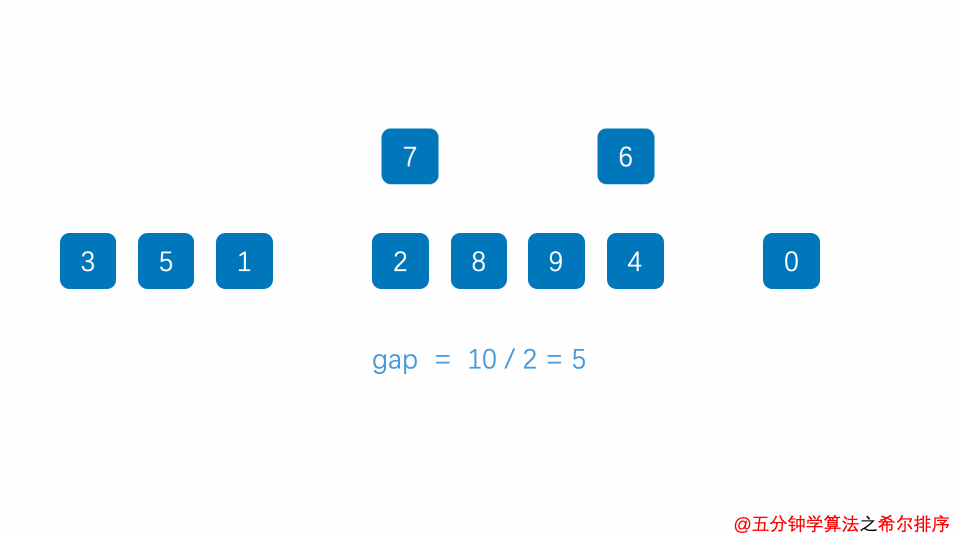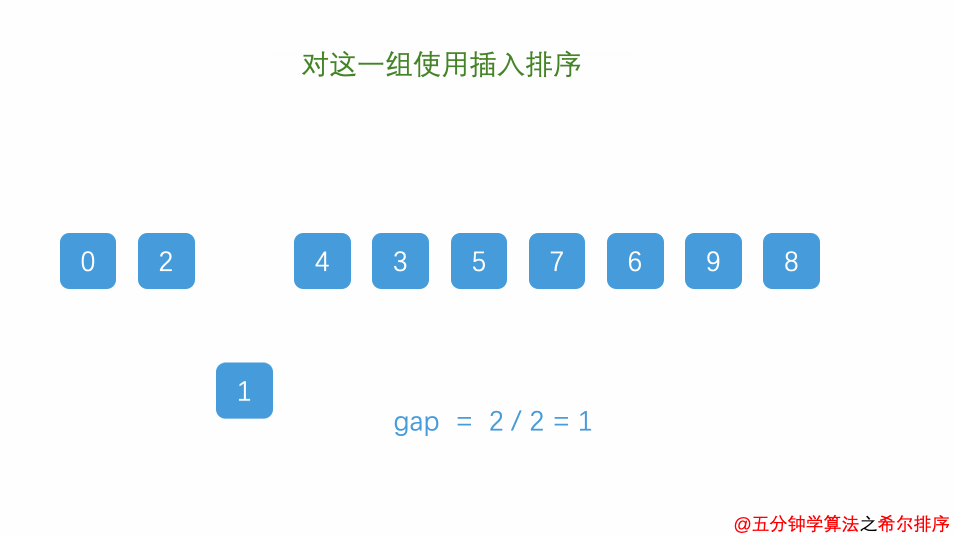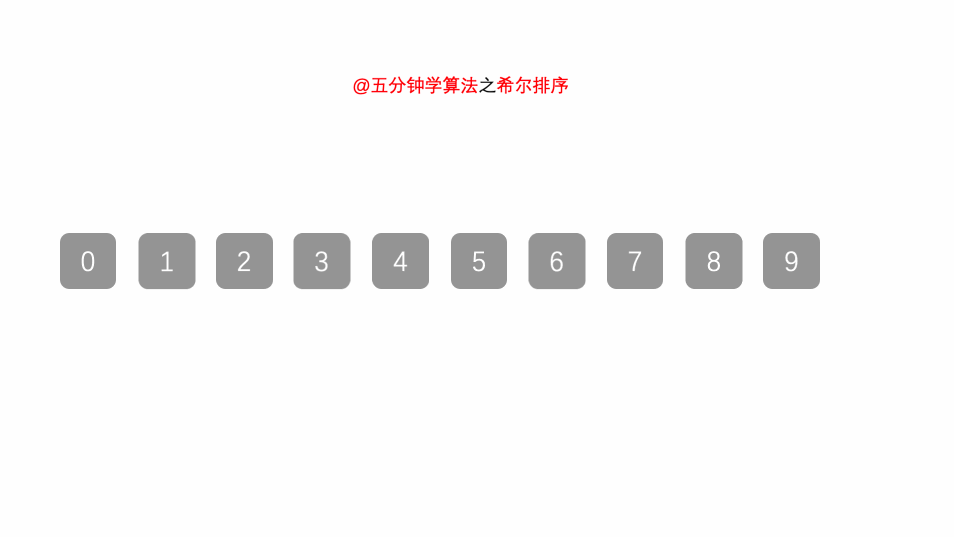
一般间隔也就是gap的选取就是数组长度的一半,如上图所示,原始数组为
[8,9,1,7,2,3,5,4,6,0],初始间隔就是5,也就是会将图中数组分为[8,3]、[9,5]、[1,4]、[7,6]、[2,0]共5组,然后对这些组合进行插入排序,并不断缩小gap(每次缩小一半),重复进行插入排序操作,最终就能够得到有序数组~
对分组不太理解的可以看下图,非常清晰:
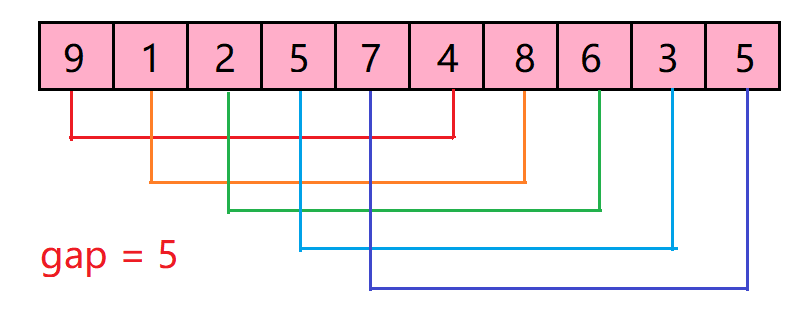
代码实现
代码的话还是循环,只需要在插入排序外层再加一层循环控制gap 的缩小即可,就是改良版的插入排序(需要对比图片和插入排序的思路仔细体会),具体代码如下:
/*** @author HelloCode* @blog https://www.hellocode.top* @date 2023年08月10日 20:59*/
public class ShellSort {public static void main(String[] args) {int[] arr = {8,9,1,7,2,3,5,4,6,0};System.out.println("原数组:" + Arrays.toString(arr));shellSort(arr);System.out.println("排序后:" + Arrays.toString(arr));}public static void shellSort(int[] arr){int n = arr.length;// 两层for循环,外层不断缩小gap(每次缩小为一半)for(int gap = n / 2; gap > 0; gap /= 2){// 内层对每组进行插入排序// 这里的i还是指向第一个待插入元素(也就是gap,可以看图理解)// 此时已排序数组的最后一个元素,就应该是i - gap// 这里i的跨度就不应该是++而是 += gap(配合图更好理解)for(int i = gap;i < n; i ++){int current = arr[i]; // 当前待插入元素int pre = i - gap; // 有序部分的最后一个元素下标// 当 i 位置元素大于等于 pre 位置元素时说明已经有序,就继续i+= gapwhile(pre >= 0){// 已经是正确位置,直接退出循环if(current >= arr[pre]){break;}// 位置不正确,需要寻找正确位置arr[pre + gap] = arr[pre];pre -= gap;}//此时pre下标的值是负数了,将current的值放到pre变量加上一个gap的位置上arr[pre + gap] = current;}}}
}
测试:
原数组:[8, 9, 1, 7, 2, 3, 5, 4, 6, 0]
排序后:[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
优化
- 希尔排序的性能高度依赖于步长序列的选择。选择不同的步长序列可能会对排序效率产生影响。
- 一些常见的步长序列包括希尔步长序列(h = n/2, n/4, n/8, …)、Sedgewick步长序列等。
- 通过尝试不同的步长序列,可以选择合适的步长来优化希尔排序的性能。
总结
优点
- 相对于传统的插入排序,希尔排序通过将元素分组进行排序,减少了逆序对的数量,从而加快了排序过程。
- 希尔排序是原地排序算法,只需在原始数组上进行元素的交换和移动,不需要额外的辅助空间。
缺点
- 希尔排序的最坏情况时间复杂度并不稳定,通常在 O(n^2) 到 O(n log n) 之间。虽然平均情况下性能较好,但在某些特定情况下,性能可能不如其他高级排序算法。
- 步长序列的选择对性能产生影响,选择不当可能导致排序效率下降。
复杂度
- 时间复杂度:取决于步长序列的选择,通常在 O(n log n) 到 O(n^2) 之间。
- 空间复杂度:原地排序,空间复杂度为 O(1)。
使用场景
- 希尔排序适用于中等规模的数据集,对于大规模数据,其性能可能不如其他更高级的排序算法。
- 在实际应用中,希尔排序的性能可能会比预期的好,尤其在某些特定情况下,例如对部分有序的数据进行排序时。
当使用希尔排序时,应特别注意其时间和空间复杂度的说明是基于最坏情况下的估计。这样的估计可能会高于实际情况。希尔排序在某些实际应用中可能表现得比预期的要好。
相关文章:

【数据结构与算法】十大经典排序算法-希尔排序
🌟个人博客:www.hellocode.top 🏰Java知识导航:Java-Navigate 🔥CSDN:HelloCode. 🌞知乎:HelloCode 🌴掘金:HelloCode ⚡如有问题,欢迎指正&#…...

docker 常用命令
1. 搜索并下载镜像 docker search bundlefusion # 搜索docker pull jhljx/bundlefusion # 将远程仓库文件下载到本地2. 用镜像创建容器 docker run -it --namebundlefusion colec777/bundlefusion-cu11.4-cudagl:v8 /bin/bash # 创建并运行 exit # 退出终端 sudo docker cont…...
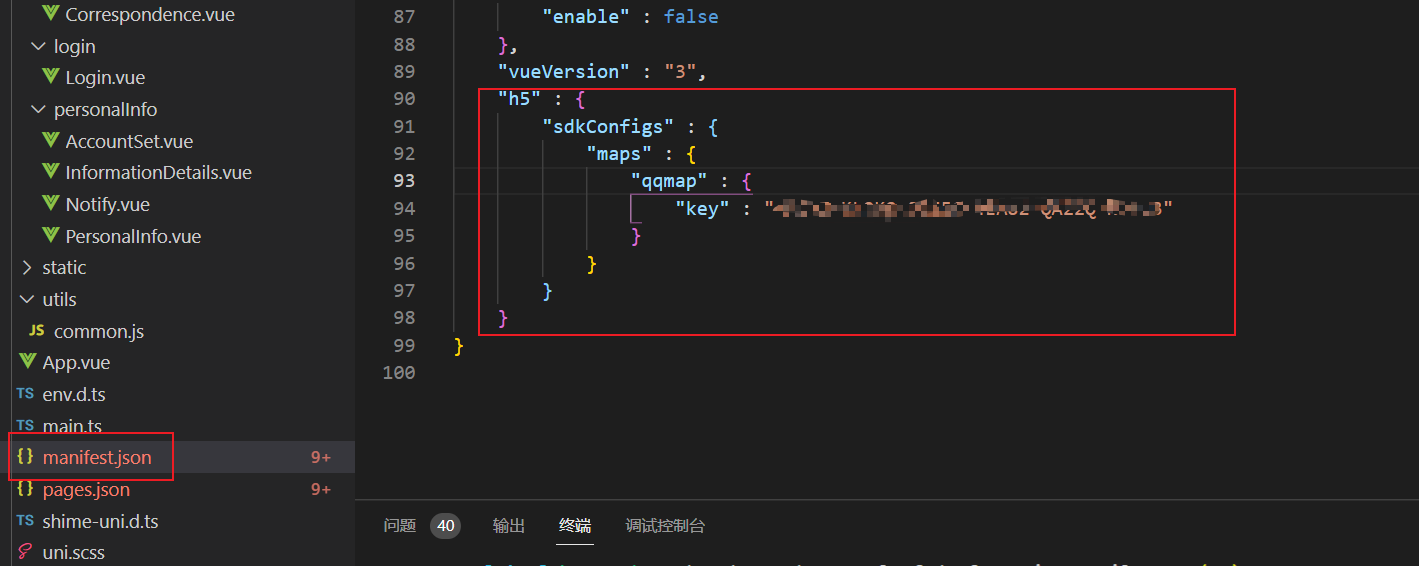
uniapp微信小程序中打开腾讯地图获取用户位置信息
实现的效果 第一步:首先登录微信公众平台 , 需要用到AppID 第二步: 注册登录腾讯位置服务 注册需要手机号和邮箱确认,然后创建应用 创建后点击添加key 添加后会生成key,后面会用到这个key 第三步: 登录微信公众平台&a…...
嵌入式领域:人才供需失衡,发展潜力巨大
嵌入式技术正快速发展,ARM处理器、嵌入式操作系统、LINUX等技术助力嵌入式领域崛起。然而,行业新颖且门槛高,缺乏专业指导。因此,嵌入式人才稀缺,身价水涨船高。 未来几年,嵌入式系统将在信息化、智能化、…...

python 书籍
python高手进阶之路 10册 QQ:417398600...

Debian纯净系统安装php常用扩展和程序
适用于 php-fpm debian容器 mysql扩展 docker-php-ext-install pdo_mysql docker-php-ext-install mysqliredis扩展 pecl install redis docker-php-ext-enable redis# pecl无法装就: docker-php-source extract # 创建并初始化 /usr/src/php目录(扩展…...
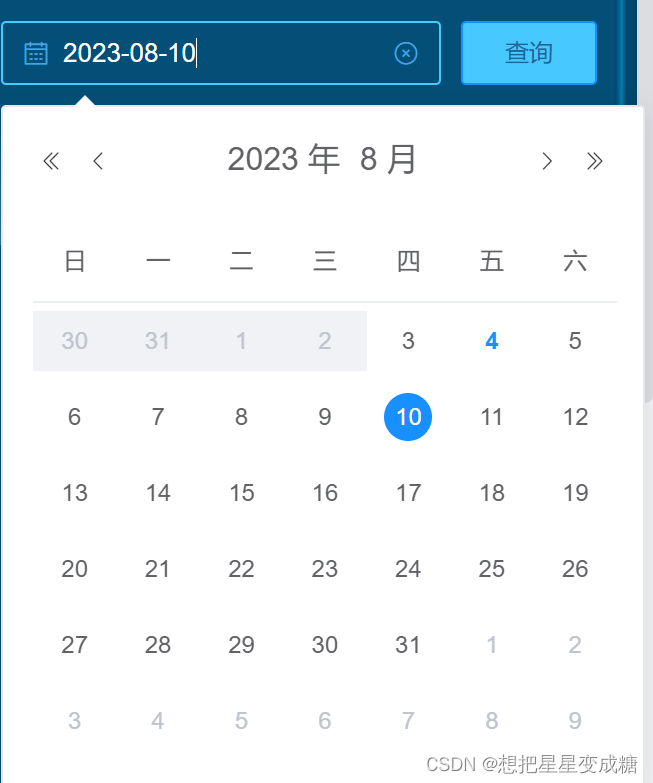
vue+element中如何设置单个el-date-picker开始时间和结束时间关联
功能:选了开始时间,则结束时间只能选择开始时间之后的;选了结束时间,则开始时间只能选择结束时间之前的 重点是picker-options属性 图示: 代码展示: // body 内部<el-form-item><el-date-pickerv-model&qu…...

二次封装ajax和axios
ajax app.config.globalProperties.$http function(url, method, data, async, fun) {$.ajax({url: baseUrl url, //请求地址type: method, //请求方式dataType: json, //数据类型contentType: "application/json",xhrFields: { //跨域设置withCredentials: t…...
Android进阶之SeekBar动态显示进度
SeekBar 在开发中并不陌生,默认的SeekBar是不显示进度的,当然用吐司或者文案在旁边实时显示也是可以的,那能不能移动的时候才显示,默认不显示呢,当然网上花哨的三方工具类太多了,但是我只是单纯的想在SeekBar的基础上去添加一个可以跟随移动显示的气泡而…...

企业计算机服务器中了locked勒索病毒怎么办,如何预防勒索病毒攻击
计算机服务器是企业的关键信息基础设备,随着计算机技术的不断发展,企业的计算机服务器也成为了众多勒索者的攻击目标,勒索病毒成为当下计算机服务器的主要攻击目标。近期,我们收到很多企业的求助,企业的服务器被locked…...
大麦订单截图 一键生成订单截图
新版付款图样式展示 这个样式图就是在大麦刚付款完的一个订单截图,它的状态是等待卖家发货 下滑下载源码 下载源码:https://pan.baidu.com/s/16lN3gvRIZm7pqhvVMYYecQ?pwd6zw3...
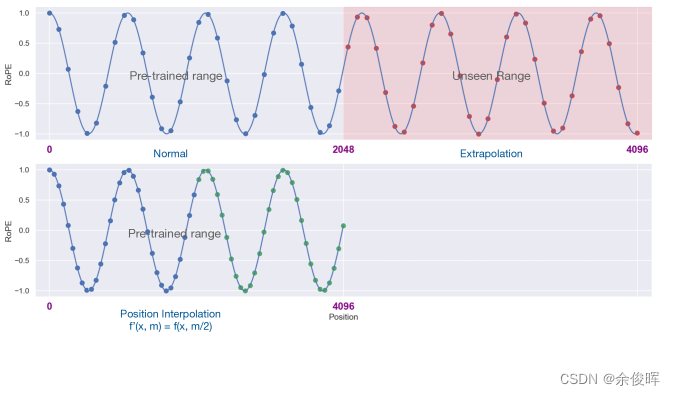
LLaMA长度外推高性价比trick:线性插值法及相关改进源码阅读及相关记录
前言 最近,开源了可商用的llama2,支持长度相比llama1的1024,拓展到了4096长度,然而,相比GPT-4、Claude-2等支持的长度,llama的长度外推显得尤为重要,本文记录了三种网络开源的RoPE改进方式及相…...

中国信息安全测评中心CISP家族认证一览
随着国家对网络安全的重视,中国信息安全测评中心根据国家政策、未来趋势、重点内容陆续增添了很多CISP细分认证。 今日份详细介绍,部分CISP及其子品牌相关认证内容,一定要收藏哟! 校园版CISP NISP国家信息安全水平考试ÿ…...

牛客网【面试必刷TOP101】~ 06 递归/回溯
牛客网【面试必刷TOP101】~ 06 递归/回溯 文章目录 牛客网【面试必刷TOP101】~ 06 递归/回溯[toc]BM55 没有重复项数字的全排列(★★)BM56 有重复项数字的全排列(★★)BM57 岛屿数量(★★)BM58 字符串的排列(★★)BM59 N皇后问题(★★★)BM60 括号生成(★★)BM61 矩阵最长递增路…...
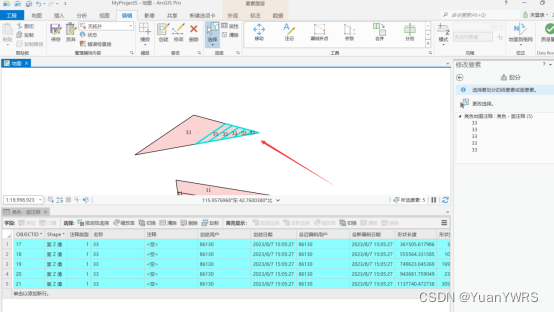
ArcGIS Pro基础:【划分】工具实现等比例、等面积、等宽度划分图形操作
本次介绍【划分】工具的使用,如下所示,为该工具所处位置。使用该工具可以实现对某个图斑的等比例面积划分、相等面积划分和相等宽度划分。 【等比例面积】:其操作如下所示,其中: 1表示先选中待处理的图斑,2…...

括号匹配问题:栈的巧妙应用与代码优化【栈、优化、哈希表】
当解决算法问题时,灵活使用数据结构是至关重要的。在这个问题中,我们需要判断一个只包含括号的字符串是否有效,即括号是否能够正确匹配和闭合。使用栈这一数据结构可以很好地解决这个问题。 题目链接:有效的括号 解题思路…...

vue项目正确使用样式deep穿透
经常开发前端的程序员应该都知道前端一般都是组件化开发,为了避免样式污染通常会使用scoped添加属性选择器,此时如果我们想在父组件中修改子组件的样式便成了难题。其实,我们可以通过以下几种方式修改子组件样式, 组件样式穿透 …...
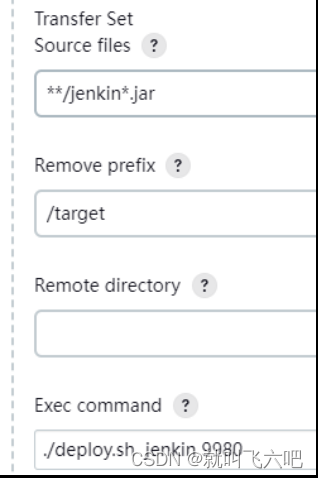
Jenkins持续集成-快速上手
Jenkins持续集成-快速上手 注:Jenkins一般不单独使用,而是需要依赖代码仓库,构建工具等。 搭配组合:GitGitee(GitHub、GitLab)MavenJenkins 前置准备 常见安装方式: war包Docker容器实例&…...

查看linux 所有运行的应用和端口命令
要查看 Linux 中所有运行的应用程序及其对应的端口,可以使用以下命令: 1. 使用 netstat 命令(已被弃用,建议使用 ss 命令): netstat -tuln 这会显示当前系统上所有打开的网络连接和监听的端口。其中&#…...

Maven安装与配置,Eclipse配置Maven【图文并茂的保姆级教程】
🥳🥳Welcome Huihuis Code World ! !🥳🥳 接下来看看由辉辉所写的关于Maven的相关操作吧 目录 🥳🥳Welcome Huihuis Code World ! !🥳🥳 一.Maven是什么? 二.Maven的下…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...
