0基础学C#笔记09:希尔排序法
文章目录
- 前言
- 一、希尔排序的思想
- 二、使用步骤
- 总结
前言
希尔排序可以说是插入排序的一种变种。无论是插入排序还是冒泡排序,如果数组的最大值刚好是在第一位,要将它挪到正确的位置就需要 n - 1 次移动。也就是说,原数组的一个元素如果距离它正确的位置很远的话,则需要与相邻元素交换很多次才能到达正确的位置,这样是相对比较花时间了。希尔排序就是为了加快速度简单地改进了插入排序,交换不相邻的元素以对数组的局部进行排序。
一、希尔排序的思想
采用插入排序的方法,先让数组中任意间隔为 h 的元素有序,刚开始 h 的大小可以是 h = n / 2,接着让 h = n / 4,让 h 一直缩小,当 h = 1 时,也就是此时数组中任意间隔为1的元素有序,此时的数组就是有序的了。
为方便理解我还准备了图片:

如果还是不懂的话我还给你准备了优质的文章讲解:希尔排序
二、使用步骤
public class ShellSort {public static int[] shellSort(int arr[]) {if (arr == null || arr.length < 2) return arr;int n = arr.length;// 对每组间隔为 h的分组进行排序,刚开始 h = n / 2;for (int h = n / 2; h > 0; h /= 2) {//对各个局部分组进行插入排序for (int i = h; i < n; i++) {// 将arr[i] 插入到所在分组的正确位置上insertI(arr, h, i);}}return arr;}/*** 将arr[i]插入到所在分组的正确位置上* arr[i]] 所在的分组为 ... arr[i-2*h],arr[i-h], arr[i+h] ...*/private static void insertI(int[] arr, int h, int i) {int temp = arr[i];int k;for (k = i - h; k > 0 && temp < arr[k]; k -= h) {arr[k + h] = arr[k];}arr[k + h] = temp;}
}
总结
需要注意的是,对各个分组进行插入的时候并不是先对一个组排序完了再来对另一个组排序,而是轮流对每个组进行排序。
性质:
1、时间复杂度:O(nlogn)
2、空间复杂度:O(1)
3、非稳定排序
4、原地排序
相关文章:

0基础学C#笔记09:希尔排序法
文章目录 前言一、希尔排序的思想二、使用步骤总结 前言 希尔排序可以说是插入排序的一种变种。无论是插入排序还是冒泡排序,如果数组的最大值刚好是在第一位,要将它挪到正确的位置就需要 n - 1 次移动。也就是说,原数组的一个元素如果距离它…...

DOCKER的容器
1. 什么是Container(容器) 要有Container首先要有Image,也就是说Container是通过image创建的。 Container是在原先的Image之上新加的一层,称作Container layer,这一层是可读可写的(Image是只读的࿰…...
跳跃游戏——力扣55
文章目录 题目描述解法一 贪心题目描述 解法一 贪心 bool canJump(vector<int>& nums){int n=nums....
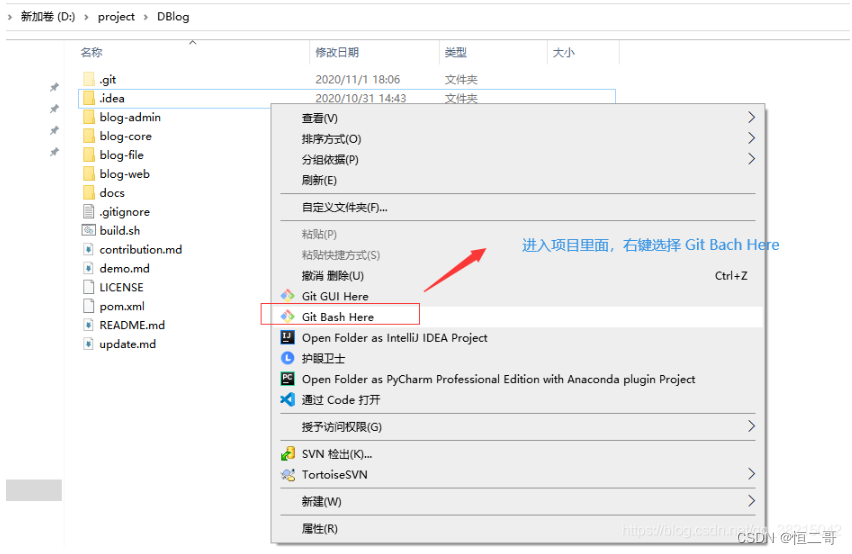
将本地项目上传至gitee的详细步骤
将本地项目上传至gitee的详细步骤 1.在gitee上创建以自己项目名称命名的空项目2.进入想上传的项目的文件夹,然后右键点击3. 初始化本地环境,把该项目变成可被git管理的仓库4.添加该项目下的所有文件5.使用如下命令将文件添加到仓库中去6.将本地代码库与远…...

iOS开发-导航栏UINavigationBar隐藏底部线及透明度
iOS 导航栏UINavigationBar隐藏底部线及透明度 苹果官方给出的解释: 如果你不调用方法设置一张背景图片的话,那就给你默认一张,然后同时还有一张阴影图片被默认设置上去,这就是导航栏上1px黑线的由来。 解决办法: 方…...

题目:2520.统计能整除数字的位数
题目来源: leetcode题目,网址:2520. 统计能整除数字的位数 - 力扣(LeetCode) 解题思路: 逐位判断即可。 解题代码: class Solution {public int countDigits(int num) {int res0;int ori…...
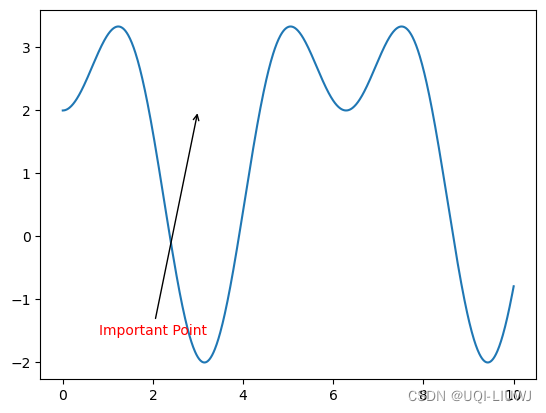
matplotlib 笔记 注释annotate
在图中的特定位置添加文本注释、箭头和连接线,以便更清晰地解释图形中的数据或信息 主要参数 text文本内容xy箭头指向的目标点的坐标xytext注释文本的坐标arrowprops 一个字典,指定注释箭头的属性,如颜色、箭头样式等 没有arrowprops的时候…...

Windows 无法安装到这个硬盘。选中的磁盘具有MBR分区。在EFI系统上,Windows只能安装到GPT磁盘
Windows无法安装到这个磁盘,选中的磁盘具有MBR分区表的解决方法 - 知乎 (zhihu.com) Windows无法安装到这个磁盘 选中的磁盘具有MBR分区表 - 知乎 (zhihu.com) 选中的磁盘具有MBR分区表,在EFI系统上,windows只能安装到GPT磁盘_选中的磁盘具有mbr分区表…...
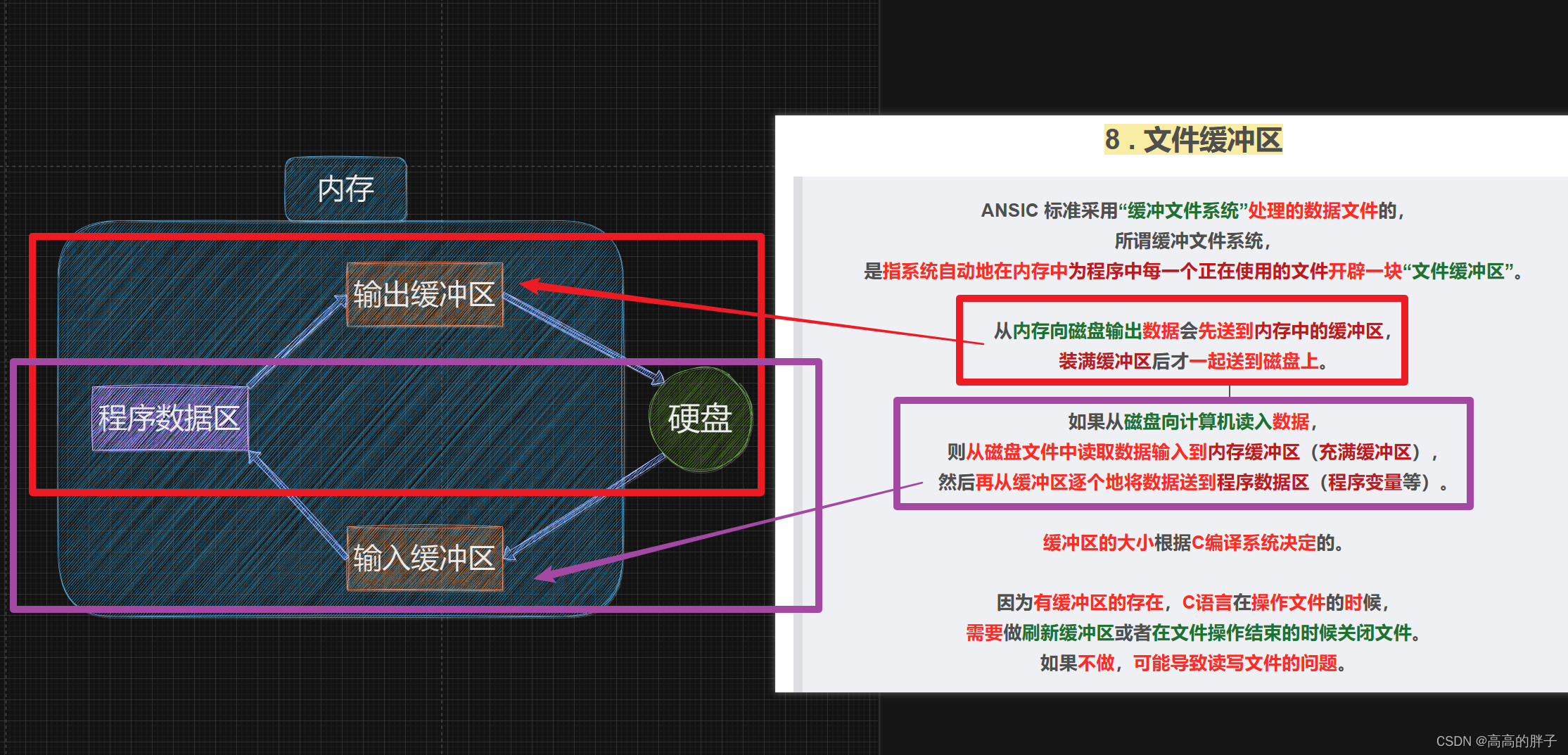
学C的第三十三天【C语言文件操作】
相关代码gitee自取: C语言学习日记: 加油努力 (gitee.com) 接上期: 学C的第三十二天【动态内存管理】_高高的胖子的博客-CSDN博客 1 . 为什么要使用文件 以前面写的通讯录为例,当通讯录运行起来的时候,可以给通讯录中增加、删…...

线性表的基本操作及在顺序存储及链式存储的实现
目录 线性表的基本操作:线性表的在顺序存储上的实现 线性表的基本操作: 一个数据结构的基本操作是指其最核心、最基本的操作。其他较复杂的操作可通过其基本操作来实现。线性表的主要操作如下 - InitList(&L):初始化表。构造一个空的线性表- Length…...

合宙Air724UG LuatOS-Air script lib API--nvm
nvm Table of Contents nvm nvm.init(defaultCfgFile, burnSave) nvm.set(k, v, r, s) nvm.sett(k, kk, v, r, s) nvm.flush() nvm.get(k) nvm.gett(k, kk) nvm.restore() nvm.remove() nvm 模块功能:参数管理 nvm.init(defaultCfgFile, burnSave) 初始化参数存储管…...

springboot单元测试的详细介绍
当开发一个复杂的应用程序时,确保代码的正确性和稳定性至关重要。在这方面,单元测试是一个不可或缺的工具,它可以帮助开发人员验证代码的各个部分是否按预期工作。Spring Boot提供了丰富的测试支持,使编写和执行单元测试变得更加容…...

Apache Doris 入门教程26:资源管理
为了节省Doris集群内的计算、存储资源,Doris需要引入一些其他外部资源来完成相关的工作,如Spark/GPU用于查询,HDFS/S3用于外部存储,Spark/MapReduce用于ETL, 通过ODBC连接外部存储等,因此我们引入资源管理机制来管理Do…...

【金融量化】Python实现根据收益率计算累计收益率并可视化
1 理论 理财产品(本金100元) 第1天:3% :(13%) ✖ 100 103 第2天:2% :(12%)✖ 以上 103 2.06 第3天:5% : (15%)✖ 以上…...

解读spring中@Value 如何将配置转自定义的bean
实现方式 着急寻求解决方式的猿友先看这块 定义配置转化类 public class UserConverter implements Converter<String, List<User>> {Overridepublic List<User> convert(String config) {if (StringUtils.isEmpty(config)) {return Collections.emptyLis…...

前端开发实习总结参考范文(合集)
▼前端开发实习总结篇一 今天就简单聊聊上面的StrutsSpringHibernate吧。 Struts 代表:表示层;Spring代表:业务逻辑层;Hibernate则代表持久层。他们是目前在Java Web编程开发中用得最多的框架,其实这样区分是为了适应软件开发过程中各个分工…...
)
♥ vue中$forceUpdate()
♥ vue中$forceUpdate() 1、认识 强制该组件重新渲染 鉴于 Vue 的全自动响应性系统,这个功能应该很少会被用到 $forceUpdate()迫使vue实例重新(rander)渲染虚拟DOM,注意并不是重新加载组件。 结合vue的生命周期,调用…...
Java一般用于postgis空间数据库通用的增删查改sql命令
目录 1 增加 2 删除 3 查询 4 更新 "public"."JGSQGW_Geo"为某模式下得表 一般postgrel有这样的设计模式 1 增加 #前端绘制出的数据插入 INSERT INTO "public"."JGSQGW_Geo" ( "geom","gridone","gridon…...

【C++类和对象】类有哪些默认成员函数呢?(上)
目录 1. 类的6个默认成员函数 2. 构造函数(*^▽^*) 2.1 概念 2.2 特性 3. 析构函数(*^▽^*) 3.1 概念 3.2 特性 4. 拷贝构造函数(*^▽^*) 4.1 概念 4.2 特性 5. 赋值运算符重载(*^▽^*) 5.1 运算符重载 5.2 赋值运算符重载 ヾ(๑╹◡╹)ノ"人总要为…...
(docker)mysql镜像拉取-创建容器-容器的使用【个人笔记】
【容器的第一次创建】 容器的第一次创建,需要先下载镜像,从 镜像拉取 0、可以搜索镜像的版本 docker search mysql1、先拉取MySQL的镜像,默认拉取最新版,使用下面的命令拉取mysql镜像 docker pull mysql也可以指定mysql的版本…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...
