P1941 [NOIP2014 提高组] 飞扬的小鸟
代码部分前有一千六百字了
P1941 [NOIP2014 提高组] 飞扬的小鸟 考察对背包 dp 算法过程理解的透彻性。过程透彻性也是解决所有问题的关键(建立在算法已学的基础上)。
n , m n,m n,m 的范围足够我们 O ( n m ) O(nm) O(nm) 的遍历整个地图。设 f i , j f_{i,j} fi,j 表示到 ( i , j ) (i,j) (i,j) 格子时的最小点击数,考虑转移,共两种情况,分别是由前一个格子下移(即不动)或上移 x x x 次得到的。由于下移操作只有选或不选两种情况,我们可以把下移操作当作 01 背包来转移,即 f i j = min ( f i , j , f i − 1 , j + d o w n [ i − 1 ] ) f_{i}{j}=\min(f_{i,j},f_{i-1,j+down[i-1]}) fij=min(fi,j,fi−1,j+down[i−1])。
上移操作可以进行多次,如果对于每个格点上移操作分别进行 0 0 0 至 m / u p [ i ] m/up[i] m/up[i] 次的转移显然会超时,观察发现,单独对 f i , j f_{i,j} fi,j 进行上移操作的转移时, f i , j = min ( f i , j , f i − 1 , j − u p [ i − 1 ] × x ) f_{i,j}=\min(f_{i,j},f_{i-1,j-up[i-1]\times x}) fi,j=min(fi,j,fi−1,j−up[i−1]×x) 与 f i , j = min ( f i , j , min ( f i − 1 , j − u p [ i − 1 ] , f i , j − u p [ i − 1 ] ) ) f_{i,j}=\min(f_{i,j},\min(f_{i-1,j-up[i-1]},f_{i,j-up[i-1]})) fi,j=min(fi,j,min(fi−1,j−up[i−1],fi,j−up[i−1])) 的本质相同,而这正是完全背包算法过程的关键。
既然本质相同,那么转移方法便与完全背包保持一致性。注意到由于每个点不能同时选择上移和下移,而上移操作的转移用到了 f i , j − u p [ i − 1 ] f_{i,j-up[i-1]} fi,j−up[i−1] 即当前列某一位置的值,由上可知在对上移操作的转移中,使用到的 f i , j − u p [ i − 1 ] f_{i,j-up[i-1]} fi,j−up[i−1] 不能包含下移操作的更新,即使用到的 f i , j − u p [ i − 1 ] f_{i,j-up[i-1]} fi,j−up[i−1] 必须只包含上移操作的更新状态。
那么这里有两种方法,一种是将两次操作的转移分开,因为下移操作的转移需要用到的 f i − 1 , j − 1 + d o w n [ i − 1 ] f_{i-1,j-1+down[i-1]} fi−1,j−1+down[i−1] 为前一列的值,且两种操作的转移都不会干扰前一列的值,所以可以先更新上移操作,再更新下移操作。
另一种是新增一维状态,设 f i , j , 0 / 1 f_{i,j,0/1} fi,j,0/1 表示 ( i , j ) (i,j) (i,j) 由上一列下移 /上移得到。思维量很小,但显然没有第一种方法简便。(我用的就是这种(
注意上移时高度到了 m m m 将无法再上升,但和 0 0 0 处不同,冲到 m m m 高度不会使游戏结束。
所以转移时高度超过 m m m 的部分要参与 dp ,并转移至 m m m 那。
最后考虑柱子和是否能通关的判断。对于柱子,首先记得排序,可以在转移完毕之后将柱子所在处的 f f f 值再赋为 inf \inf inf,也可以干脆在转移过程前标记,转移时就特判掉并跳过,当然也不可以不这么麻烦(猜对了我就这么敲的,调半天不对(
通关判断就很简单了,转移完扫一遍当前列有没有解,到不了就退出,通过柱子数为当前柱子编号 − 1 -1 −1,当前列过不了肯定说明有柱子(因为无论如何都可以一直按屏幕保持在 m m m 高度),当前柱子过不了自然过了的柱子就是编号 − 1 -1 −1 了。
时间复杂度 O ( n m ) O(nm) O(nm)。
空间复杂度 O ( n m ) O(nm) O(nm),可以滚掉一维,故为 O ( m ) O(m) O(m)。
#include<bits/stdc++.h>
using namespace std;
int n,m,k,up[10005],down[10005],f[2][2005][2];
struct qh{int p,l,h;bool operator < (const qh &T)const {return p<T.p;}
}a[10005];
inline int Rd(){int s=0,w=1;char ch=getchar();while (ch<'0'||ch>'9'){if(ch=='-') w=-1;ch=getchar();}while (ch>='0'&&ch<='9') s=(s<<1)+(s<<3)+ch-'0',ch=getchar();return s*w;
}
int main(){n=Rd();m=Rd();k=Rd();for(int i=0;i<n;i++) up[i]=Rd(),down[i]=Rd();for(int i=1;i<=k;i++) a[i]=(qh){Rd(),Rd(),Rd()};sort(a+1,a+k+1);
// for(int i=1;i<=k;i++) printf("%d %d %d\n",a[i].p,a[i].l,a[i].h);int z=0;for(int i=1;i<=n;i++){for(int j=1;j<=m*2;j++) f[i%2][j][0]=f[i%2][j][1]=1e9;for(int j=1;j<=m*2;j++){if(j+down[i-1]<=m) f[i%2][j][0]=min(f[(i-1)%2][j+down[i-1]][0],f[(i-1)%2][j+down[i-1]][1]);if(j-up[i-1]>0) f[i%2][j][1]=min(f[i%2][j-up[i-1]][1],min(f[(i-1)%2][j-up[i-1]][0],f[(i-1)%2][j-up[i-1]][1]))+1;}for(int j=m+1;j<=m*2;j++) f[i%2][m][1]=min(f[i%2][m][1],f[i%2][j][1]);if(a[z+1].p==i){z++;for(int j=1;j<=a[z].l;j++) f[i%2][j][0]=f[i%2][j][1]=1e9;for(int j=a[z].h;j<=m*2;j++) f[i%2][j][0]=f[i%2][j][1]=1e9;
// printf("%d %d %d %d\n",z,a[z].p,a[z].l,a[z].h);}int mn=1e9;for(int j=1;j<=m;j++) mn=min(mn,min(f[i%2][j][0],f[i%2][j][1]));
// for(int j=1;j<=m;j++) printf("%d %d ",f[i%2][j][0],f[i%2][j][1]);puts("");if(mn==1e9) return printf("0\n%d",z-1),0;}int ans=1e9;for(int i=1;i<=m;i++) ans=min(ans,min(f[n%2][i][0],f[n%2][i][1]));printf("1\n%d",ans);return 0;
}
/*
start coding:09:44
finish debiuging:11:05
*/
附上题目:
[NOIP2014 提高组] 飞扬的小鸟
题目描述
Flappy Bird 是一款风靡一时的休闲手机游戏。玩家需要不断控制点击手机屏幕的频率来调节小鸟的飞行高度,让小鸟顺利通过画面右方的管道缝隙。如果小鸟一不小心撞到了水管或者掉在地上的话,便宣告失败。
为了简化问题,我们对游戏规则进行了简化和改编:
游戏界面是一个长为 n n n,高为 m m m 的二维平面,其中有 k k k 个管道(忽略管道的宽度)。
小鸟始终在游戏界面内移动。小鸟从游戏界面最左边任意整数高度位置出发,到达游戏界面最右边时,游戏完成。
小鸟每个单位时间沿横坐标方向右移的距离为 1 1 1,竖直移动的距离由玩家控制。如果点击屏幕,小鸟就会上升一定高度 x x x,每个单位时间可以点击多次,效果叠加;如果不点击屏幕,小鸟就会下降一定高度 y y y。小鸟位于横坐标方向不同位置时,上升的高度 x x x 和下降的高度 y y y 可能互不相同。
小鸟高度等于 0 0 0 或者小鸟碰到管道时,游戏失败。小鸟高度为 m m m 时,无法再上升。
现在,请你判断是否可以完成游戏。如果可以,输出最少点击屏幕数;否则,输出小鸟最多可以通过多少个管道缝隙。
输入格式
第 1 1 1 行有 3 3 3 个整数 n , m , k n, m, k n,m,k,分别表示游戏界面的长度,高度和水管的数量,每两个整数之间用一个空格隔开;
接下来的 n n n 行,每行 2 2 2 个用一个空格隔开的整数 x x x 和 y y y,依次表示在横坐标位置 0 ∼ n − 1 0 \sim n-1 0∼n−1 上玩家点击屏幕后,小鸟在下一位置上升的高度 x x x,以及在这个位置上玩家不点击屏幕时,小鸟在下一位置下降的高度 y y y。
接下来 k k k 行,每行 3 3 3 个整数 p , l , h p,l,h p,l,h,每两个整数之间用一个空格隔开。每行表示一个管道,其中 p p p 表示管道的横坐标, l l l 表示此管道缝隙的下边沿高度, h h h 表示管道缝隙上边沿的高度(输入数据保证 p p p 各不相同,但不保证按照大小顺序给出)。
输出格式
共两行。
第一行,包含一个整数,如果可以成功完成游戏,则输出 1 1 1,否则输出 0 0 0。
第二行,包含一个整数,如果第一行为 1 1 1,则输出成功完成游戏需要最少点击屏幕数,否则,输出小鸟最多可以通过多少个管道缝隙。
样例 #1
样例输入 #1
10 10 6
3 9
9 9
1 2
1 3
1 2
1 1
2 1
2 1
1 6
2 2
1 2 7
5 1 5
6 3 5
7 5 8
8 7 9
9 1 3
样例输出 #1
1
6
样例 #2
样例输入 #2
10 10 4
1 2
3 1
2 2
1 8
1 8
3 2
2 1
2 1
2 2
1 2
1 0 2
6 7 9
9 1 4
3 8 10
样例输出 #2
0
3
提示
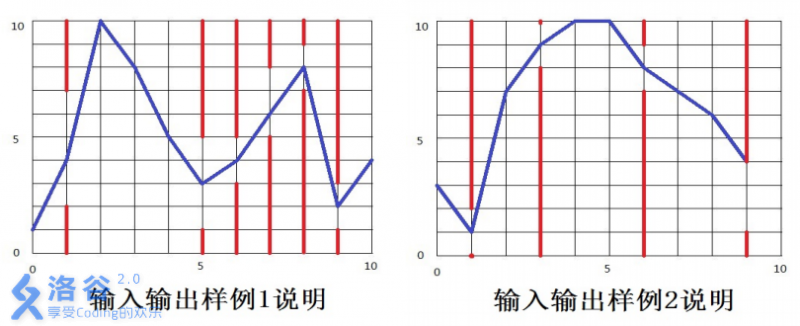
【输入输出样例说明】
如下图所示,蓝色直线表示小鸟的飞行轨迹,红色直线表示管道。
【数据范围】
对于 30 % 30\% 30% 的数据: 5 ≤ n ≤ 10 , 5 ≤ m ≤ 10 , k = 0 5 \leq n \leq 10, 5 \leq m \leq 10, k=0 5≤n≤10,5≤m≤10,k=0,保证存在一组最优解使得同一单位时间最多点击屏幕 3 3 3 次;
对于 50 % 50\% 50% 的数据: 5 ≤ n ≤ 20 , 5 ≤ m ≤ 10 5 \leq n \leq 20, 5 \leq m \leq 10 5≤n≤20,5≤m≤10,保证存在一组最优解使得同一单位时间最多点击屏幕 3 3 3 次;
对于 70 % 70\% 70% 的数据: 5 ≤ n ≤ 1000 , 5 ≤ m ≤ 100 5 \leq n \leq 1000, 5 \leq m \leq 100 5≤n≤1000,5≤m≤100;
对于 100 % 100\% 100% 的数据: 5 ≤ n ≤ 10000 5 \leq n \leq 10000 5≤n≤10000, 5 ≤ m ≤ 1000 5 \leq m \leq 1000 5≤m≤1000, 0 ≤ k < n 0 \leq k < n 0≤k<n, 0 < x , y < m 0 < x,y < m 0<x,y<m, 0 < p < n 0 < p < n 0<p<n, 0 ≤ l < h ≤ m 0 \leq l < h \leq m 0≤l<h≤m, l + 1 < h l + 1 < h l+1<h。
start writing:19:00
finish the work:20:33
相关文章:

P1941 [NOIP2014 提高组] 飞扬的小鸟
代码部分前有一千六百字了 P1941 [NOIP2014 提高组] 飞扬的小鸟 考察对背包 dp 算法过程理解的透彻性。过程透彻性也是解决所有问题的关键(建立在算法已学的基础上)。 n , m n,m n,m 的范围足够我们 O ( n m ) O(nm) O(nm) 的遍历整个地图。设 f i , …...

Vue3+Element plus+pageHelper实现分页
安装element plus npm install element-plus --save引入 修改main.js: import { createApp } from vue import App from ./App.vue import ElementPlus from element-plus import element-plus/dist/index.cssconst app createApp(App) app.use(ElementPlus) ap…...
外贸路上那些哭笑不得的事情
前几天一个老顾客在软件上联系,说自己上次的订货体验很满意,货物的质量很好,而且服务和回复也很及时, 比起他之前的供货商要好很多,他之前的供货商虽然货物的质量也很好,但是每次询问问题都是要等好久才给…...
双端列表 —— Deque 接口概述,使用ArrayDeque实现队列和双端队列数据结构
Deque接口简介 Deque译为双端队列,在双向都能作为队列来使用,同时可用作栈。Deque接口的方法是对称成比例的。 Deque接口继承Queue接口,因此具有Queue,Collection,Iterable的方法属性。 双端队列的工作原理 在常规队…...

构建可观测架构,从这5个方面着手
随着系统复杂度的提升,“可观测性”(Observability)成为架构建设的重要原则之一。那么构建一个可观测的系统架构需要做哪些工作呢?本文将从以下5个方面介绍构建可观测架构的主要考虑: 1.定义指标和度量,明确关键业务指标需求 首先要确定核心业务指标,比如请求响应…...
每天10个小知识点)
前端面试的性能优化部分(7)每天10个小知识点
目录 系列文章目录前端面试的性能优化部分(1)每天10个小知识点前端面试的性能优化部分(2)每天10个小知识点前端面试的性能优化部分(3)每天10个小知识点前端面试的性能优化部分(4)每天…...

【云原生】kubernetes中容器的资源限制
目录 1 metrics-server 2 指定内存请求和限制 3 指定 CPU 请求和限制 资源限制 在k8s中对于容器资源限制主要分为以下两类: 内存资源限制: 内存请求(request)和内存限制(limit)分配给一个容器。 我们保障容器拥有它请求数量的…...

java Long型数据返回到前端失进度问题解决
直接在springmvc配置中增加信息转换。亲测可用。简单粗暴 Override public void configureMessageConverters(List<HttpMessageConverter<?>> converters) {MappingJackson2HttpMessageConverter jackson2HttpMessageConverter new MappingJackson2HttpMessageCo…...

【设计模式】-策略模式:优雅处理条件逻辑
Java 策略模式之优雅处理条件逻辑 前言 在软件开发中,我们经常会遇到根据不同的条件执行不同逻辑的情况。这时,策略模式是一种常用的设计模式,能够使代码结构清晰、易于扩展和维护。 本文将详细介绍策略模式的概念及其在Java中的应用&#x…...

SpringBoot整合多数据源
SpringBoot整合多数据源 在实际企业项目开发中,我们经常会在SpringBoot项目中配置多数据源,一方面可以减缓数据库压力,另一方面可以也是业务需求的场景 下面就来看看如何在SpringBoot项目中配置多数据源 POM 在配置多数据源之前ÿ…...
CLIP论文精度
CLIP论文精度 Zero-shot CLIP多模态模型 Image Endecoder是一个图片编码器,既可以是ResNet,也可以是Vision Transformer. Text Encoder和Image Encoder产生的两组特征进行对比学习(无监督训练) 分类头?“分类头” 是指网络结…...
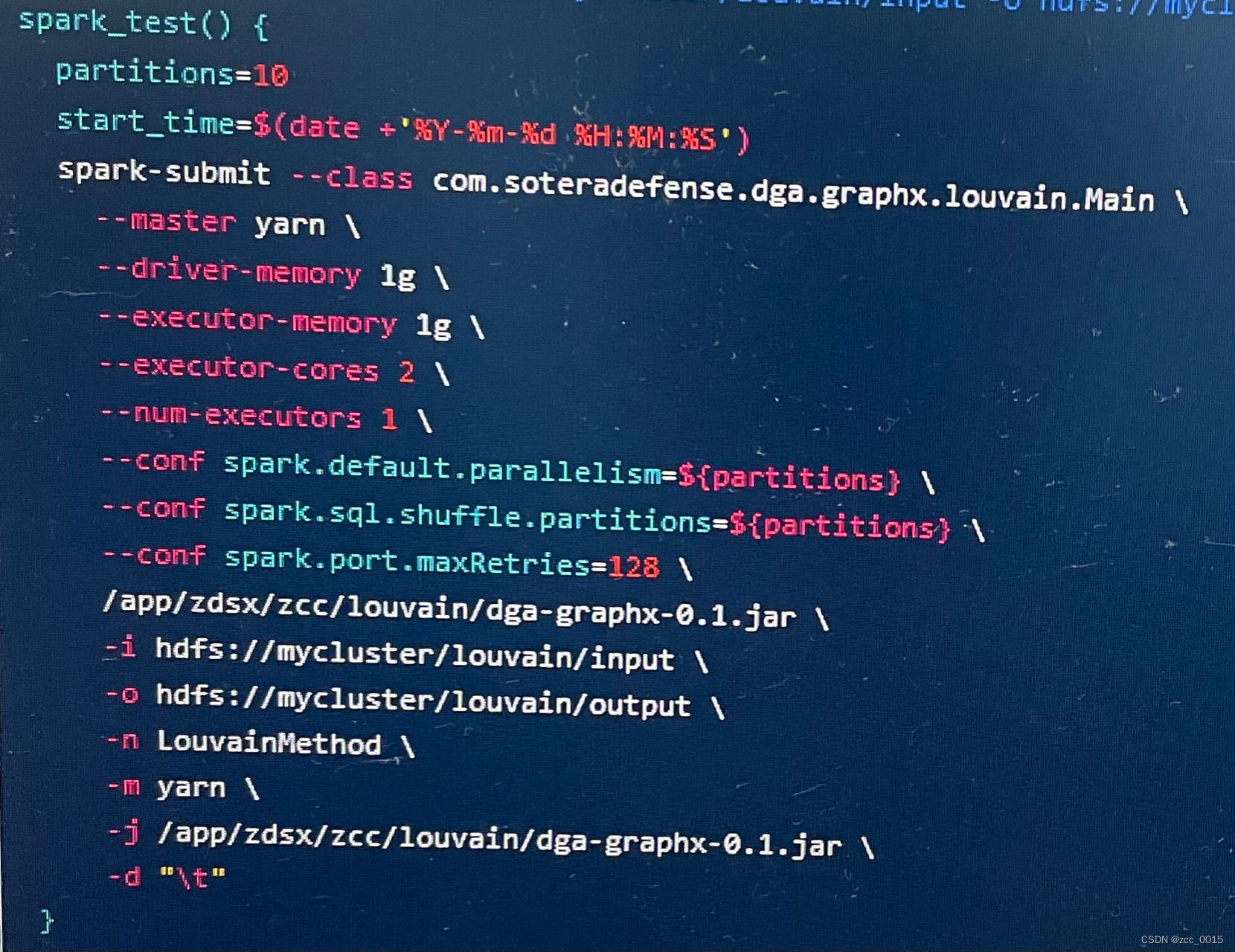
LouvainMethod分布式运行的升级之路
1、背景介绍 Louvain是大规模图谱的谱聚类算法,引入模块度的概念分二阶段进行聚类,直到收敛为止。分布式的代码可以在如下网址进行下载。 GitHub - Sotera/spark-distributed-louvain-modularity: Spark / graphX implementation of the distri…...
【Node.js】低代码平台源码
一、低代码简介 低代码管理系统是一种通过可视化界面和简化的开发工具,使非专业开发人员能够快速构建和管理应用程序的系统。它提供了一套预先定义的组件和模块,使用户可以通过拖放操作来设计应用程序的界面和逻辑。低代码管理系统还提供了自动化的工作…...

docker 部署 xxl-job-admin
1、先安装mysql docker pull mysql 2、运行mysql 容器 ( 端口 3306 容器名称 mysql 密码 123456 ) docker run -d --name mysql -e MYSQL_ROOT_PASSWORD123456 -p 3306:3306 mysql 3、将tables_xxl_job.sql文件(官网地址:http…...

c++(空间配置器)[32]
空间配置器 一级空间配置器 || 二级空间配置器 默认先走二级然后判断 二级空间配置器 一个指针指向start_free然后start_free向后移动,相当于哈希桶的头删和头插 8byte:切大补小 C的二级空间配置器按照8字节(或者更大的倍数)切分…...

Linux系列之解压文件
一.欢迎来到我的酒馆 使用命令解压Linux文件。 目录 一.欢迎来到我的酒馆二.使用命令解压文件 二.使用命令解压文件 2.1解压 .tar.gz文件: tar -zxvf 文件名.tar.gz.tar,gz这种文件是tar文件的压缩文件,因此可以使用tar命令进行解压 -zxvf命令参数&…...

为什么重写equals方法时必须重写hashcode方法
与 equals的区别 如果两个引用类型变量使用运算符,那么比较的是地址,它们分别指向的是否是同一地址的对象,结果一定是false,因为两个对象地址必然不同。 不能实现比较对象的值是否相同。 所有对象都有equals方法,默认…...

java导入excel图片处理
直接看代码吧,主要逻辑吧excel的图片拿到 压缩上传获取url // 将文件转成XSSFWorkbook工作簿XSSFWorkbook wb new XSSFWorkbook(uploadFile);// 获取工作薄中第一个excel表格XSSFSheet sheet wb.getSheetAt(0);// 核心:::获取ex…...
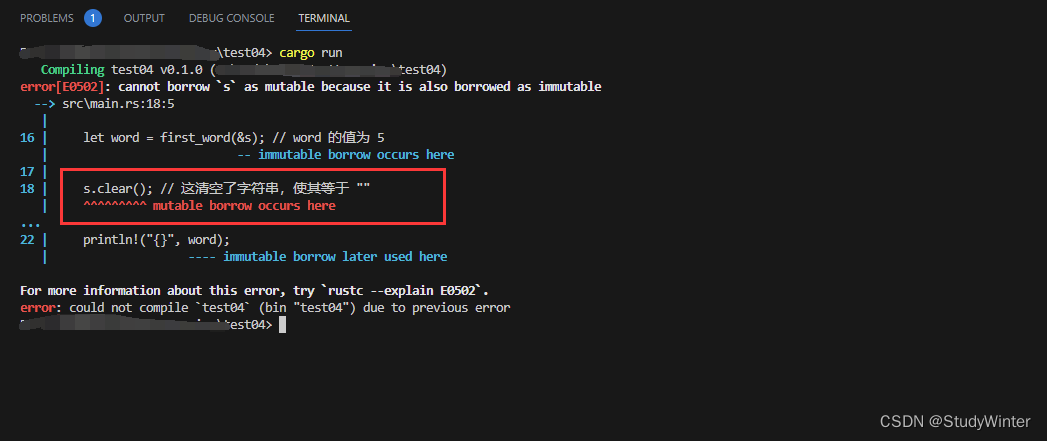
【Rust】Rust学习 第四章认识所有权
第四章认识所有权 所有权(系统)是 Rust 最为与众不同的特性,它让 Rust 无需垃圾回收(garbage collector)即可保障内存安全。因此,理解 Rust 中所有权如何工作是十分重要的。 4.1 所有权 所有运行的程序都…...
学习C语言第三天 :关系操作符、逻辑操作符
1.关系操作符 C语言用于比较的表达式,称为“关系表达式”里面使用的运算符就称(relationalexpression),为“关系运算符” (relationaloperator) ,主要有下面6个。 > 大于运算符 < 小于运算符 > 大于等于运算符 < 小于等…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...

用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章
用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章 摘要: 操作系统内核的安全性、稳定性至关重要。传统 Linux 内核模块开发长期依赖于 C 语言,受限于 C 语言本身的内存安全和并发安全问题,开发复杂模块极易引入难以…...

深度解析云存储:概念、架构与应用实践
在数据爆炸式增长的时代,传统本地存储因容量限制、管理复杂等问题,已难以满足企业和个人的需求。云存储凭借灵活扩展、便捷访问等特性,成为数据存储领域的主流解决方案。从个人照片备份到企业核心数据管理,云存储正重塑数据存储与…...
